基于曲面拟合模型的山区GNSS水准精度分析

房新玉，陆伟，姚晓伟

（交通运输部天津水运工程科学研究所水运工程测绘技术研究中心，天津300456）

基于曲面拟合模型的山区GNSS水准精度分析

房新玉，陆伟，姚晓伟

（交通运输部天津水运工程科学研究所水运工程测绘技术研究中心，天津300456）

介绍了测量中的高程系统及其转换关系，对GNSS水准模型进行了简要介绍。通过实例对山区GNSS水准曲面拟合的精度进行了分析，并对GNSS水准精度和外围点的精度进行了评定，得到了一些有工程价值的结论。

GNSS；高程拟合；正常高；大地高；拟合精度

GNSS水准高程拟合研究是为了实现由GNSS大地高求出水准高，用GNSS水准代替几何水准，提高GNSS水准测量的精度，发挥GNSS技术提供三维坐标的优越性［1-2］。

采用GNSS测定正高或正常高，成为GNSS水准。通过GNSS测出的是大地高，要确定点的正高或正常高，需要进行高程系统转换，即确定大地水准面差距或高程异常［1-3］。

大地高程系统是以参考椭球面为基准面的高程系统，它是一个几何量，不具有物理意义。GNSS定位测量获得的是WGS-84坐标系下高精度的大地高，大地高一般用H表示［4-5］。

正高是以大地水准面为基准面的高程系统，它是唯一确定的数值，可以用来表示地面点的高程，但由于地壳质量分布的不均匀，正高不可能准确求定，正高用Hg表示。

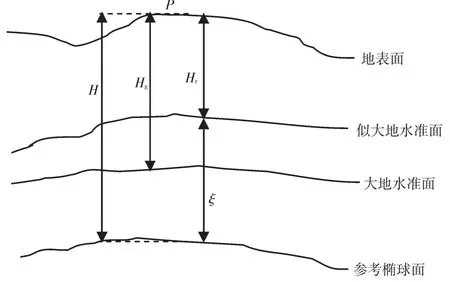
图1 大地高、正高、正常高关系图Fig.1 Relationship of geodetic height，orthogonal height and normal height

正常高是以似大地水准面为基准的高程系统，正常高用Hr表示［4-5］。

似大地水准面到参考椭球面的距离成为高程异常，用ξ表示。大地高和正常高的关系可以表示为

如果高程异常已知，通过式（1）就能进行大地高和正常高之间的相互转换，但当其未知时，则需要设法确定高程异常的数值。确定高程异常的基本方法有天文大地法、大地水准面模型法、重力测量法和几何内插法及残差模型等方法。下面以几何内插法为例，介绍高程拟合的方法［4-5］。并利用曲面拟合模型对GNSS水准在山区的拟合精度进行分析。

1 几何内插法的数学模型

几何内插法的基本原理就是通过一些既进行了GNSS观测，又进行了水准测量的公共点获得相应的高程异常，采用平面或曲面拟合、配置、三次样条等内插方法，拟合出测区的高程异常面，进而求出待求点的正常高［1-2］。

在进行多项式内插时，可采用不同阶次的多项式。假定（x,y）为测区内任一点的高程异常，其高程异常值为ξ

f(x,y)为测区内高程异常拟合的数学模型。则可将高程异常表示为下面的多项式形式零次多项式（常数拟合）

一次多项式（平面拟合）

二次多项式（曲面拟合）

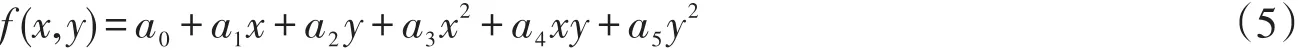
若采用零次多项式进行内插，至少需要1个公共点；若采用一次多项式进行内插，至少需要3个公共点；若采用二次多项式进行内插，至少需要6个公共点。然后利用最小二乘原理解算出多项式系数，从而确定测区的高程异常曲面，利用拟合出的曲面，内插出其他GNSS点的高程异常，从而求出各个待求点的正常高。

零次多项式适用于高程异常变化平缓的地区，如果GNSS和水准联测点较高的情况，在控制点周围4 km范围内，可以达到3 cm的精度［6］。

一次多项式适用于高程异常变化平缓的地区且控制点较少的情况，它的精度情况与GNSS水准联测点的分布和精度情况有关，它的拟合精度要高于零次多项式的拟合精度而低于二次多项式拟合的精度［7］。

二次多项式适用于控制点较多的情况，可以应用于流域、平原和山区，它的精度情况与GNSS水准联测点的分布和精度情况有关，精度要优于一次多项式拟合的精度［6-7］。

2 实例分析及拟合精度

2.1 实例分析

测区位于南方某沿海地区，3条河流自西向东贯穿该地区，3条河流之间为山区，测区东西向长约65 km，南北向长约78 km，测区范围为3 400 km2，共有水准联测点39个，其水准为二等，部分为三等，分布情况如图2所示。

2.2 观测值权阵确定

高程异常的精度受GNSS和准测量精度的双重影响，根据公式（1）可知

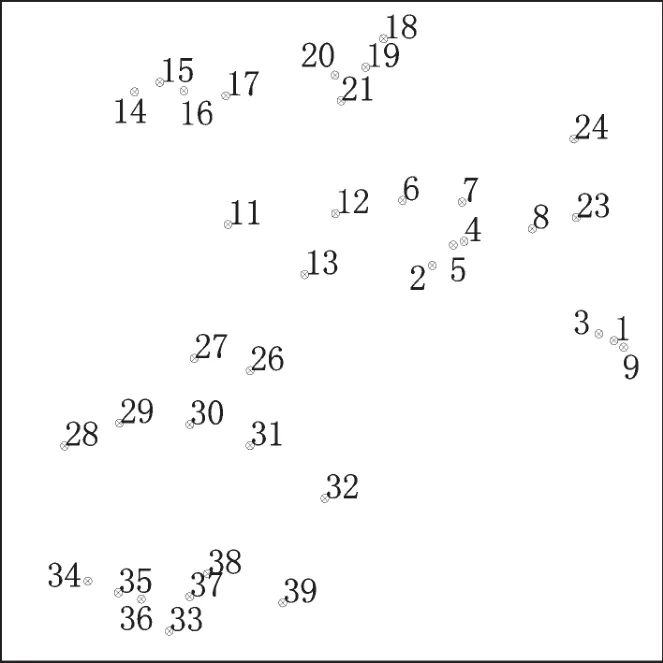
图2 水准联测点点位分布图Fig.2 Distribution of benchmark

GNSS静态大地高的精度与二等水准测量的精度相同［8］，根据水准测量规范规定的各个等级水准的限差要求，设定GNSS大地高和水准的权重如表1，并依此推定高程异常的权。

2.3 拟合精度分析

在对数据粗差点10，22，25进行剔除后，按以下5种方案采用曲面拟合法对测区拟合情况进行分析。

表1GNSS大地高和水准的权Tab.1 Weight of GNSS geodetic height and benchmark

（1）点位均匀分布于整个测区，选择控制点5，9，12，14，18，24，26，34，39共9个点作为拟合点，其余点作为校核点；（2）点位均匀分布于测区中部，选择控制点2，7，11，21，26，30，32，38共8个点作为拟合点，其余点作为校核点；（3）点位均已分布于测区北部，选择控制点2，6，9，11，14，18，21，24共8个点作为拟合点，其余点作为校核点；（4）点位均匀分布于整个测区，选择控制点3，5，13，15，19，31，35，38共8个点作为校核点，其余点作为拟合点；（5）采用分区拟合，分北部、中部、南部三区分别进行拟合，区与区之间有公共点。控制点11、13作为北部和中区部拟合的分界点和公共点，控制点28、32作为中部和南部区域的分界点和公共点。分区拟合时，分别在北部选择4、12、16校核点，中部选择27、29作为校核点，南部选择35、38作为校核点。

从表2中可以看出：

（1）拟合点的高程异常之差小于校核点，显然，这是因为拟合模型是依靠拟合点高程异常数据建立起来的；（2）方案1的内符合精度、外符合精度均较大，大于5 cm，这是由于拟合点较少，且拟合的面积较大造成的；（3）方案4的内符合精度大于5 cm、外符合精度均较小，这是由于拟合区域较大，造成内符合精度较大；参与拟合的点较多，因此外符合精度较小；（4）方案2、方案3和方案5的内符合精度、控制点覆盖范围内的外符合精度均较小；这是由于拟合的区域较小；（5）方案2和方案3控制点覆盖范围外的外符合精度比较大，因此，控制点覆盖范围外的不能应用该拟合结果。

2.4GNSS水准精度评定

内符合精度和外符合精度是绝对精度评定的方法，相对精度的评定为根据检核点至已知点的距离L（km），按几何水准限差计算检核点拟合残差的限值（表2），将残差与限值比较，评定GNSS水准的精度。

以方案3为例，对控制点覆盖范围内的GNSS水准精度进行评定，该表中：平均值内符合精度；外符合精度

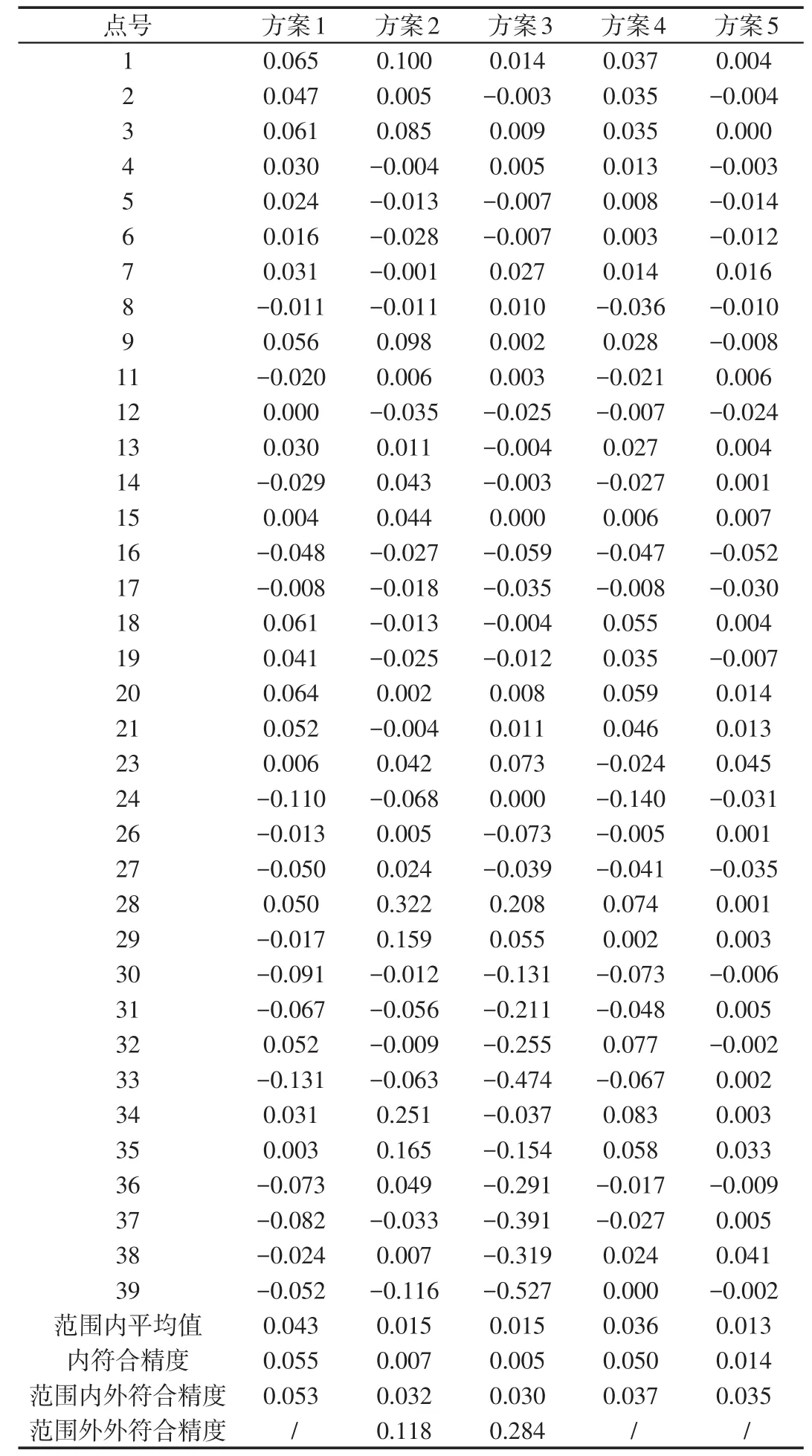
表2 不同方案高程异常拟合结果与几何水准计算异常结果之差值Tab.2 Difference of height anomaly fitting results using different schemes and geometric leveling m

表3GNSS水准限差［11］Tab.3 Tolerance of GNSS benchmark

图3GNSS水准精度评定点位分布图

Fig.3 Distribution of GNSS benchmark accuracy evaluation区域东西长约60 km，南北宽约38 km，面积约1 325 km2，控制点分布情况如图3所示。

根据方案3和表3，得到了GNSS水准精度评定情况，如表4所示。

除了16、23号控制点高程异常差值在四等限差和等外限差之间，其他点均满足三等水准测量精度需求；16号点距最近14号点的实地距离约为9.2 km，此时的四等限差为0.061 m，满足四等规范要求；23号点距最近的24号点实地距离约为14 km，此时的四等限差为0.075 m，拟合精度满足四等规范要求。从图3中可以看出，23号点位于测区边缘，且距测区最近参与拟合控制距离较远，因此，在测区边缘，参与拟合的控制点间距尽可能的不要太大。

从以上分析GNSS水准的拟合精度满足四等水准测量精度的要求，大部分情况可以满足三等水准测量精度的要求。

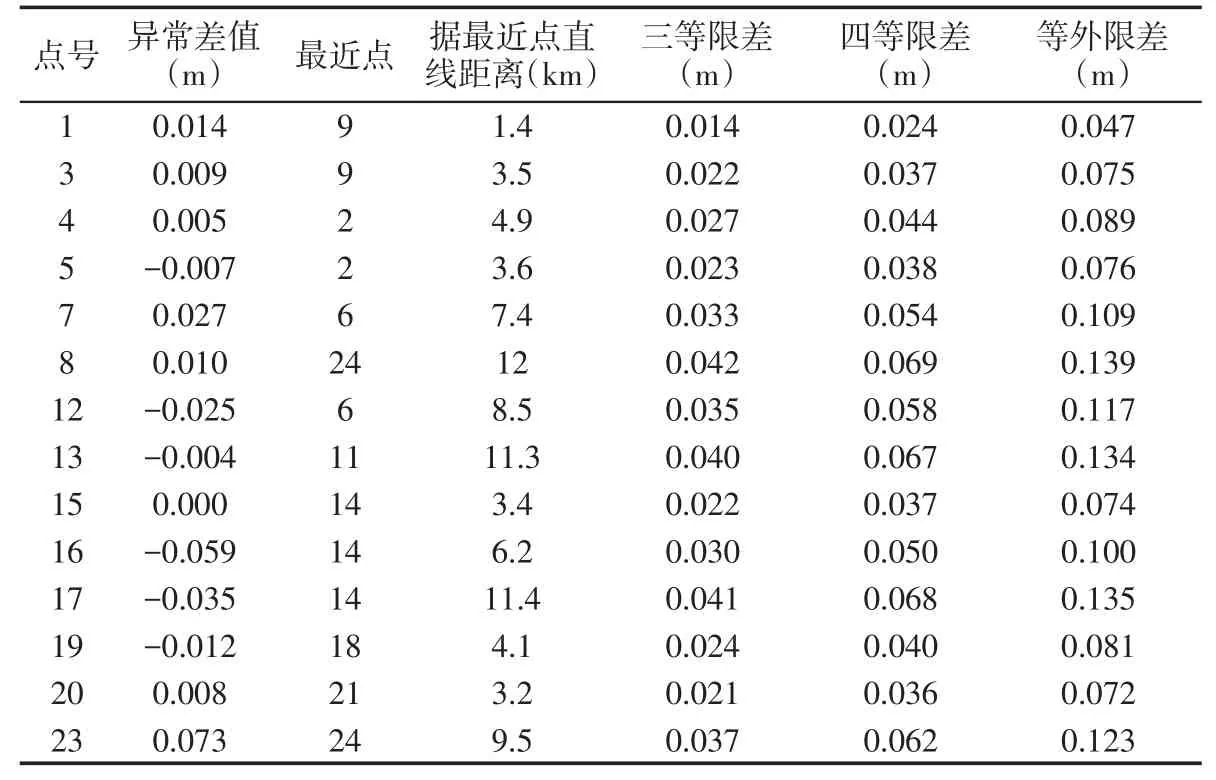
表4GNSS水准精度评定表Tab.4 GNSS benchmark accuracy evaluation

2.5 外围点的精度评定

各种拟合模型都不宜外推，但在实际工作中，测区的GNSS点不可能全部都包含在已知点连成的几何图形内。对这些外围点，GNSS水准计算时只能外推，为了校核GNSS水准外推精度，从1、9号点按三等水准测量精度要求联测了3个水准点40、41、42，并对GNSS水准外推精度进行了校核。方案如图4所示，图4中带三角形的点为拟合点，其他点为校核点，拟合区域东西长54 km，南北长28 km。从而得到了GNSS水准外围点精度评定情况，如表5所示。

从表5中可以看出，拟合点东侧区域外围25 km的控制点差值均在四等限差范围以内，南侧外围20 km的控制点均在等外限差以内，经分析可知，这是由于拟合区域东西向较南北向长，因此在同样距离下，东侧区域外侧的精度较好。在四等限差精度限差的要求下，东侧外推长长度比约为25/54≈1/3，在等外限差精度限差的要求下，南北侧外推长度比约为20/28≈2/3。这个结论仅对本项目适用，要具体问题具体分析，在验证合格后方可使用。

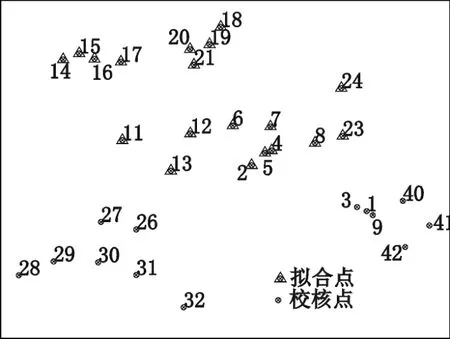
图4GNSS水准外围点精度估算控制点分布图Fig.4 Distribution of GNSS benchmark peripheral point evaluation

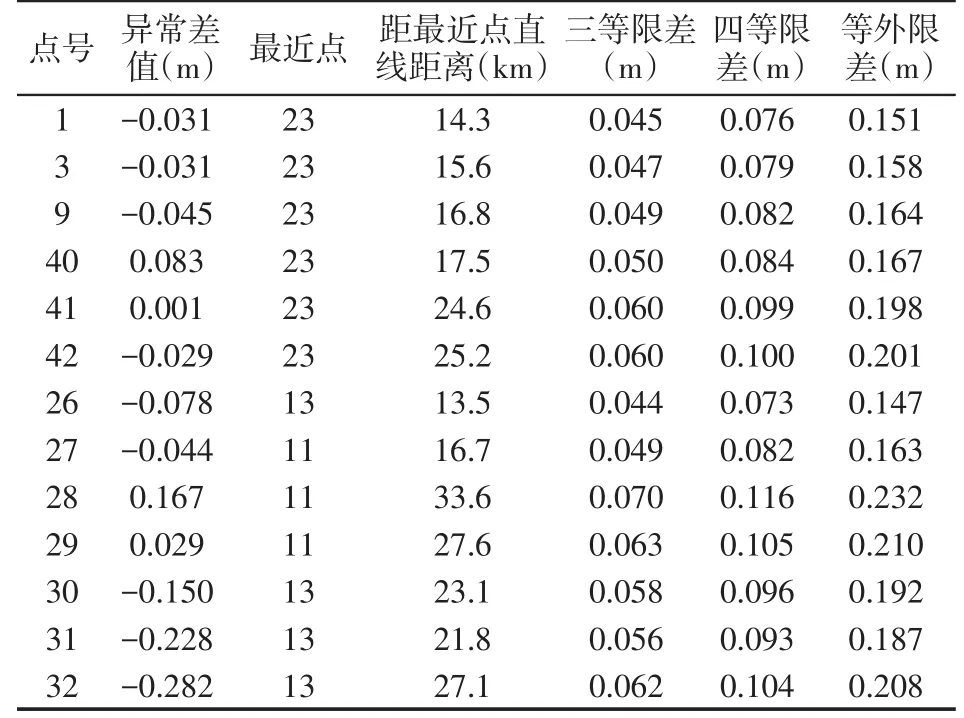
表5GNSS外围点精度评定表Tab.5 GNSS benchmark peripheral point used for accuracy

3 结论

GNSS水准拟合的精度不仅与起算点的数量有关，而且与起算点的空间分布有着密切的关系，一般来说控制点数量越多，控制点分布越均匀，拟合精度越高；在面积较大的区域，建议采用分区拟合的方法进行拟合，各区之间要有公共点；在控制点密度足够时，采用GNSS水准拟合可以满足四等水准测量精度的需求；GNSS水准外围点在拟合区域外围1/3可以达到四等水准测量精度。但需要指出的是，GNSS拟合的精度与模型精度，区域高程异常变化的复杂程度有关，在应用GNSS水准拟合时，一定要有检核，并且在检核点精度满足要求时方可使用。

［1］李征航，黄劲松.GPS测量与数据处理［M］.武汉：武汉大学出版社，2005.

［2］杜玉柱.GNSS测量技术［M］.武汉：武汉大学出版社，2013.

［3］杨小青，胡伍生.基于神经网络的似大地水准面模型精化方法研究［J］.测绘工程，2008，17（4）：8-11. YANG X Q，HU W S.Research on the measures of accurating quasi geoid model based on Neural Network［J］.Engineering of Sur⁃veying and Mapping，2008，17（4）：8-11.

［4］焦明连.GPS⁃RTK高程拟合方法研究［J］.海洋测绘，2005，25（3）：6-11. JIAO M L.Research on the Data Fitting Method of GPS RTK Height［J］.Hydrographic Surveying and Charting，2005，25（3）：6-11.

［5］伍青云.GPS高程拟合的方式及可靠性分析［J］.现代测绘，2006，29（4）：29-31. WU Q Y.The Form of GPS Height Interpolation and Analysis of Safety［J］.Modern Surveying and Mapping，2006，29（4）：29-31.

［6］刘大杰，施一民，过静珺.全球定位系统的原理与数据处理［M］.上海：同济大学出版社，2006.

［7］胡伍生，高成发.GPS测量原理及其应用［M］.北京：人民交通出版社，2002.

［8］华锡生，黄腾.精密工程测量技术及应用［M］.南京：河海大学出版社，2002.

［9］奉光泽.GPS高程拟合精度的研究［J］.测绘学报，2008，31（6）：260-264. FENG G Z.Research on Fitting Precision of GPS Elevation［J］.Acta Geodaetica et Cartographica Sinica，2008，31（6）：260-264.

［10］雒养社，马超.GPS拟合高程精度分析［J］.中国煤田地质，2007，19（3）：77-79. LUO Y S，MA C.Precision Analysis of GPS Elevation Fitting［J］.Coal Geology of CHINA，2007，19（3）：77-79.

［11］JTS131-2012，水运工程测量规范［S］.

Analysis on precision of GNSS level base on surface fitting in mountain area

FANG Xin⁃yu,LU Wei,YAO Xiao⁃wei
(Tianjin Research Institute for Water Transport Engineering,Surveying&Mapping Technology Research Center for Water Transport Engineering,Tianjin 300456,China)

The elevation systems in measurement and their transformation relationship were introduced,and the GNSS level models were also introduced briefly.The precision of GNSS leveling surface fitting in mountain area was analyzed through examples,and the GNSS level accuracy and peripheral point accuracy were assessed,and some valuable conclusions were obtained.

Global Navigation Satellite System;height fitting;normal height;geodetic height;fitting precision

P 715

A

1005-8443（2015）02-0176-05

台州打造椒江内河样板航道

2014-04-22；

2014-08-15

房新玉（1983-），男，河南省南阳人，工程师，主要从事GPS测量数据处理研究工作。

Biography：FANG Xin⁃yu（1983-），male，engineer.

本刊从浙江省交通运输厅获悉，2015年2月25日，浙江省台州市椒江区组织开展了椒江内河样板航道建设协议签订活动。椒江内河样板航道位于台州永宁河十字泾，起点为椒江与路桥行政区域交界，终点为洪家街道永宁河段，总长1.3 km，预计工程总投资约800万元。据悉，该工程将由椒江区港航管理处负责实施，是台州市进一步响应浙江省“五水共治”政策，不断提高航道通航能力、美化两岸环境、改善周边居住条件、打造标准航段的重点工程。同时，该工程也是目前台州市计划建设的唯一的内河样板航道。（殷缶，梅深）