主桩套板结构的简化计算与优化设计

杜辰，管学鹏，刘现鹏，刘红彪

（1.天津港港务设施管理中心，天津300456；2.交通运输部天津水运工程科学研究所，天津300456）

主桩套板结构的简化计算与优化设计

杜辰1，管学鹏1，刘现鹏2，刘红彪2

（1.天津港港务设施管理中心，天津300456；2.交通运输部天津水运工程科学研究所，天津300456）

作为一种板桩结构，主桩套板结构的计算理论和设计方法仍未明确。文章结合案例提出简化计算方法，推导主桩、套板入土深度与桩板宽度比的关系式，分别采用传统m法和考虑锚碇点位移的m法计算主桩内力，并与有限元结果对比。基于ABAQUS软件建立三维桩土模型，研究不同工况下结构的力学性能，分析主桩入土深度和刚度对套板内力的影响。结果表明，主桩套板结构的锚碇点位移不可忽略，且套板宽度越小、入土越深，主桩所需的入土深度越小；主桩入土深度对结构的整体稳定有影响，随主桩入土加深套板内力逐渐趋于稳定；主桩刚度的增大能够减小套板的受力，为节省材料套板可适当减薄。

板桩结构；主桩套板结构；m法；ABAQUS

主桩套板结构［1］是传统板桩结构的改进型式，由主桩和插放在桩间的套板组成，具有结构可靠、适应性强、节省材料等优点，可应用于码头、船闸、船坞、护岸和围堰等挡水、挡土工程。但由于构件类型多，各部分受力不明确，相关研究资料较少。目前用于计算单锚板桩结构的主要方法有：以m法为代表的线弹性地基反力法、以NL法为代表的非线弹性地基反力法和以p⁃y曲线法为代表的复合地基反力法。文献［2］采用NL法计算了主桩套板结构的水平承载力，并通过ABAQUS软件研究了套板尺寸变化对主桩受力的影响，发现主桩跨中弯矩随套板宽度的增加明显提高，而套板厚度和入土深度对主桩的影响较小。与传统结构不同，主桩套板结构在泥面下缺少套板的支挡，墙前被动土压力较小，使得泥面以上部分产生较大的水平位移，而现行的m法计算时通常没有考虑锚碇点位移的影响，若设计不当将对结构的正常使用造成影响。本文根据结构特点提出主桩套板结构的简化计算方法，结合案例采用理论方法和有限元法计算主桩内力，并借助ABAQUS软件分析主桩入土深度和刚度对套板内力的影响，研究成果可供主桩套板结构设计参考。

1 工程案例

参考京唐港32#泊位的地质资料，该地区土层主要以第四纪全新统及上更新统松散沉积物为主，忽略泥面以上土的浮重度及剩余水压力、波浪力的作用。码头设计的顶面高程3.35 m，拉杆高程1.35 m，设计低水位和港池底泥面高程分别取-0.15 m和-7.00 m，码头面载为30 kPa。拉杆安设在主桩背侧，采用Φ80 mm的钢拉杆，拉杆间距取3 m，锚碇结构采用0.4 m厚、3.5 m高的地下连续板，锚碇板顶高程为2.35 m。参照桩板式挡土结构［3］，主桩截面取0.6 m×1.0 m（抗弯向），相邻主桩间距3 m，净距2.4 m。主桩间插放厚度为0.15 m的套板，套板两端分别嵌入主桩0.15 m。T形钢筋混凝土板桩的翼板和挡板式前墙的挡板底面一般低于设计泥面1 m，且不小于冲刷深度［4］，套板的入土深度取1.65 m。本地区土层参数见表1，码头断面和主桩套板截面见图1、图2。

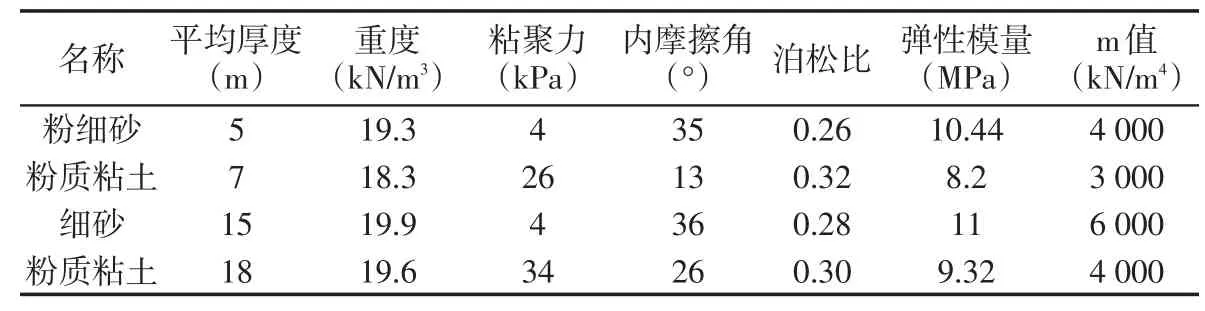
表1 土层参数Tab.1 Soil parameters

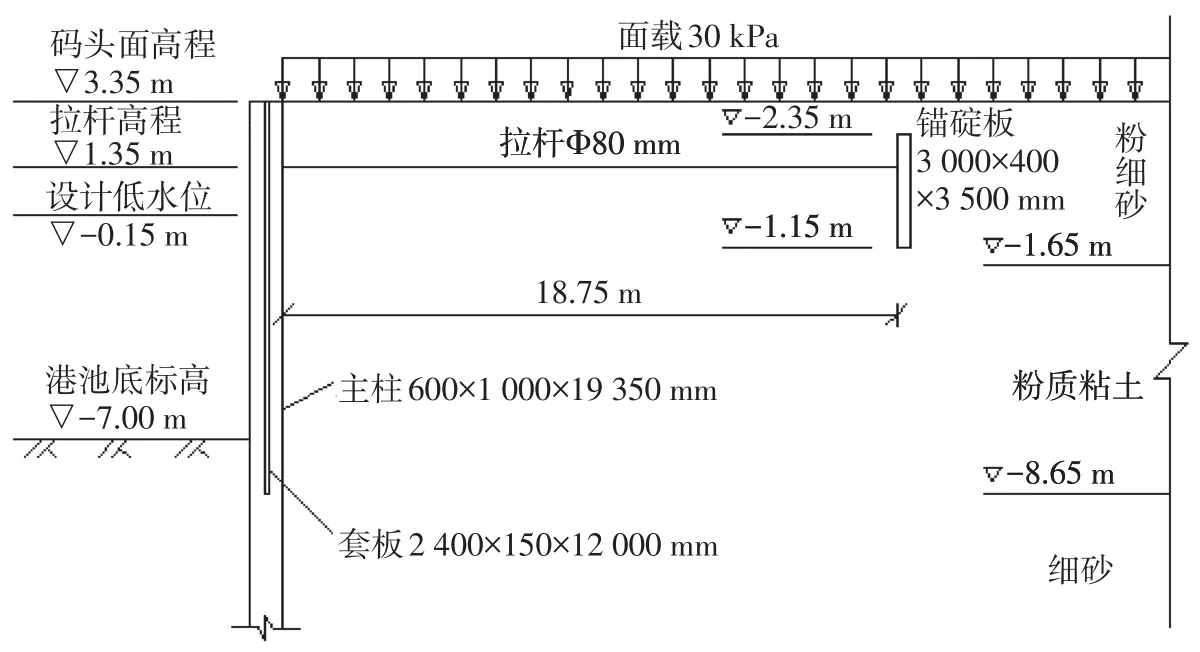
图1 板桩码头断面图Fig.1 Sectional drawing of sheet⁃pile wharf

图2 主桩套板截面图Fig.2 Sectional drawing of main pile and inlaid sheet

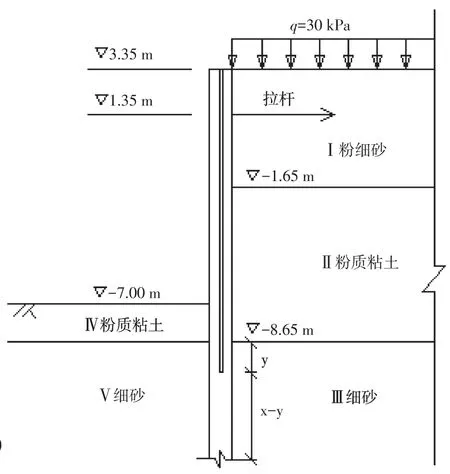
图3 土层分区域编号Fig.3 Soil region number

2 简化计算方法

理论分析、模型试验和原型观测均表明板桩结构在实际工程中表现为多次超静定，其入土部分的工作状态并非自由支承，也不是完全嵌固，板桩前墙可视作弹性竖直梁，适合采用m法进行求解。考虑到拉杆和锚碇结构对板桩内力的影响，m法通常有两种假定：（1）以锚碇点没有产生位移计算，得到的跨中最大弯矩乘以0.7～0.8的折减系数；（2）以锚碇点产生一定的位移计算，得到的跨中最大弯矩不折减。由于在泥面下一定深度处桩板不连续，主桩套板结构的墙前被动土压力较小，与传统结构相比，锚碇点的位移较大，计算中应充分考虑。

2.1 土压力计算

采用考虑粘聚力作用的平面滑动假定极限平衡原理的Coulomb经典理论［4］计算土压力。计算时按图3所示将土层分区域重新编号，假设主桩入土深度为1.65+ x，套板入土深度为1.65+y，主桩和套板的计算宽度分别为n1和n2，选取如图4所示的1根主桩和2根1/2套板作为计算单元，将平面受力问题转化为空间问题。

2.2 入土深度计算

主桩套板结构“踢脚”稳定的破坏过程符合破损阶段理论，计算入土深度时应满足“踢脚”稳定要求［4］

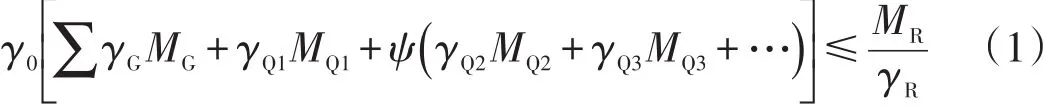
式中：γ0、γG分别为结构重要性系数和永久作用分项系数；MG为永久作用标准值产生的效应，kN·m；γQ1、γQ2、 γQ3…为可变作用分项系数；MQ1为主导可变作用效应，kN·m；ψ为作用组合系数；MQ2、MQ3…为非主导可变作用标准值产生的“踢脚”力矩，kN·m；MR为墙前被动土压力标准值对拉杆锚碇点的稳定力矩，kN·m，；γR为抗力分项系数。

将土压力计算结果代入式（1），得到反映主桩套板结构入土深度与构件宽度对应关系的表达式

式中比例系数Dc为桩板宽度比值越小，说明结构中套板所占比重越大，从而传给主桩的主动土压力也越大，主桩入土深度相应加大，如图5所示。从式（2）可以看出，主桩入土深度随套板入土深度的增加而减小，套板入土越深，泥面以下的结构段受到的被动土压力越大，抗倾覆力矩相应增加，如图6所示。

计算单元宽度按3 m取，不妨令y=0，试算得到主桩最小入土深度5.72 m。

2.3 主桩内力计算

采用m法进行计算，鉴于结构穿越多层土，取泥面下一定深度范围内各层土m值的加权平均值作为平均比例系数［5］

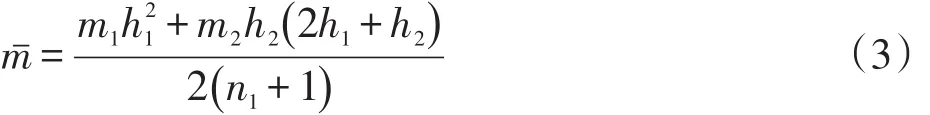
式中：m1、m2为泥面下各层土的m值，kN/m4；h1、h2为各层土的平均厚度，m。计算得到mˉ=5 202.39 kN/m4。主桩套板结构的受力状态是十分复杂的三维空间问题，涉及到桩—板—土的相互作用。在外力作用下，由于套板及桩侧摩阻力的传递作用，主桩周边有多余的土体参与受力，求解时需要假定主桩的计算宽度b0，根据文献［6］取b0=1.5n1+0.5=1.4m。换算深度h*是影响水平承载计算的另一重要参数，如果竖向弹性地基梁法中地基反力系数沿深度以线性方式增加，那么可通过式（4）确定换算深度

式中：z为主桩入土深度，m；E为桩身弹性模量，kPa，取实际值的0.85倍；I为桩截面惯性矩，m4。计算得到h*=3.2。根据挠曲微分方程，主桩在泥面处的位移x0和转角θ0可由式（5）、式（6）确定

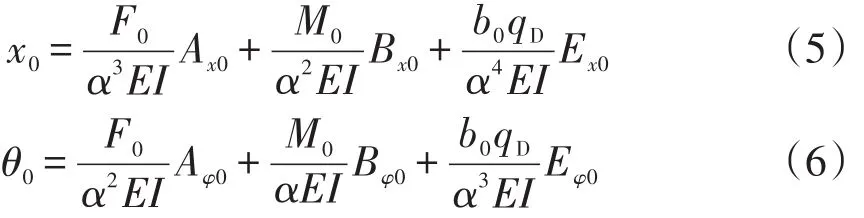
式中：F0为泥面以上土压力和拉杆拉力的合力，kN；M0为泥面以上土压力和拉杆拉力的合力对计算水底的弯矩和，kN·m；qD为泥面以上土体和码头顶面均布荷载产生的超载土压力，kN；Ax0、Bx0、Ex0、Aφ0、Bφ0、Eφ0为h*=3.2，z/h*=0时的无量纲系数，由文献［7］查得。锚碇点位移主要由拉杆伸长量λ和锚碇结构的水平位移X组成，诸未知量均可表示为拉杆拉力的函数，建立如下锚碇点位移平衡方程

式中：h0为主桩的自由高度，m；Δ为结构后方土压力在锚碇点产生的位移，m；Λ为拉杆拉力在锚碇点产生的位移，m。联立上述方程，求解出拉杆拉力411.05 kN，主桩的各项力学参数随即可得。

图4 计算单元示意图Fig.4 Schematic diagram of calculation unit

图5 主桩入土深度与桩板宽度比的关系（套板深度1.65 m）Fig.5 Relationship between main pile embedded depth and pile⁃sheet width ratio（inlaid sheet depth 1.65 m）

图6 主桩入土深度与套板入土深度的关系（桩板宽度比0.25）Fig.6 Relationship between main pile embedded depth and inlaid sheet embedded depth（pile⁃sheet width ratio 0.25）

3 有限元分析

采用ABAQUS研究主桩套板结构在土压力和地面均布荷载共同作用下的力学性能，采取以下基本假设：（1）不考虑土中排水，按总应力法进行分析；（2）土体为服从Mohr⁃Coulomb屈服准则的理想弹塑性体，同一土层为均质各向同性且结构的存在不影响土层分布；（3）考虑结构与土体的接触、滑动与脱开。

3.1 计算模型

利用对称性，选取2个桩板单元进行分析，主桩尺寸取19.35 m×0.6 m×1.0 m（高×宽×厚），套板尺寸取12 m×2.4 m×0.15 m，二者连接方式为固接；锚碇板尺寸取3.5 m×3.0 m×0.4 m；拉杆两端通过Tie约束与主桩、锚碇板绑定。对于分析单桩荷载，地基可在水平方向上取桩径的20～30倍，桩底土层厚度可取桩长的1.0～1.5倍［8］，建模时土体左边界距码头前沿25 m，右边界距锚碇板25.5 m，桩底土层厚23 m；模型前后边界为绕y平面的对称约束，左右边界为垂直x平面的链杆约束，底面为固支约束。结构与土体的共同耦合作用属于边界条件非线性问题，通过定义接触对来模拟接触。考虑到接触面的相对滑动、脱离以及周期性的闭合和张开，根据滑动规律采用点对面的小滑移来模拟相对滑动。接触面的切向作用通过罚摩擦公式定义，结构与土体的平均摩擦系数取0.5，法向作用采用只传递压力不传递拉力的“硬接触”公式。主桩、套板、锚碇板及土体均采用8节点六面体线性减缩积分单元C3D8R，并选择Hex类型划分网格，拉杆采用2节点线性空间单元T3D2，模型整体包含18 258个单元。土层参数参见表1，结构构件参数见表2，模型各部分网格划分如图7、图8所示。

表2 构件参数Tab.2 Component parameters

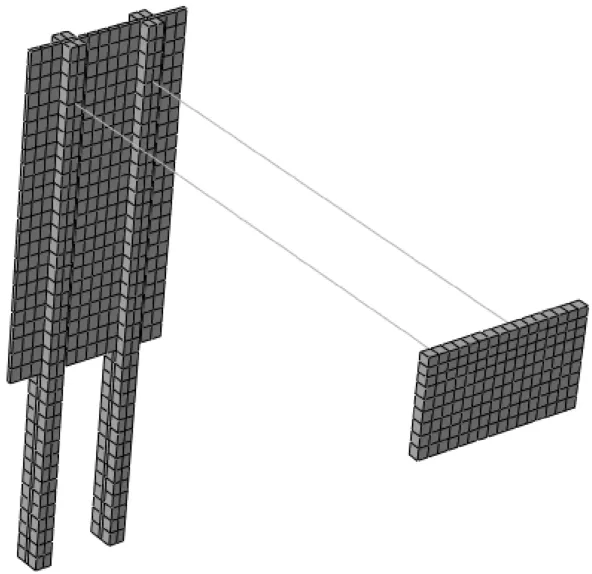
图7 结构网格划分Fig.7 Mesh for structure

图8 土体网格划分Fig.8 Mesh for soil

图9 主桩套板总应力云图Fig.9 Total stress nephogram of main pile and inlaid sheet

图10 主桩套板总位移云图Fig.10 Total displacement nephogram of main pile and inlaid sheet

3.2 计算分析

选取3种计算工况：（1）开挖港池至-6 m高程；（2）开挖港池至-7 m高程；（3）码头顶面施加30 kPa均载，加载结束后得到如图9、图10所示的后处理云图。

由图9、图10可知，主桩承担了绝大部分土压力，在泥面以上的跨中部位受力最大；与主桩相比，套板的刚度较小，产生的变形量较大，在跨中部位达到位移最大值。理论方法和有限元法的计算结果如表3、图11所示。

由表3、图11可知，考虑锚碇点位移的m法和有限元法的计算结果较为接近，在结构背侧主动土压力的作用下锚碇点发生较大位移，拉杆拉力减小，主桩在泥面处的水平位移加大。传统m法的弯矩计算值偏小，在高程-11.5 m处取最大值。与理论方法相比，有限元法在泥面处的计算值偏大，主要由于在泥面附近结构沿水平方向连续，有较多的土压力通过桩板间的剪力作用传给主桩，促使主桩的弯矩加大。不同工况下的主桩和套板弯矩变化情况如图12、图13所示。

表3 计算结果汇总Tab.3 Calculation results

图11 泥面下的主桩弯矩Fig.11 Main pile moment below mud surface

由图12可知，主桩处于弹性嵌固的工作状态，港池开挖结束后，上部最大弯矩达到694.1 kN·m，下部最大弯矩达到286.1 kN·m，均载施加结束后，上部最大弯矩达到1 016.0 kN·m，下部最大弯矩达到354.1 kN· m。受陆侧主动土压力的影响，拉杆以下的主桩弯矩逐渐增大，在-4 m高程处达到最大值，随着高程的降低，主桩弯矩逐渐减小直至为零，并在泥面下一定深度范围内产生反向弯矩。由图13可知，受尺寸的限制，套板仅产生一个方向的弯矩。与主桩相比，套板的弯矩变化范围很小，均载施加结束后最大弯矩只有6.0 kN· m，约为主桩的0.6%，且在高程最低处有反弯趋势。

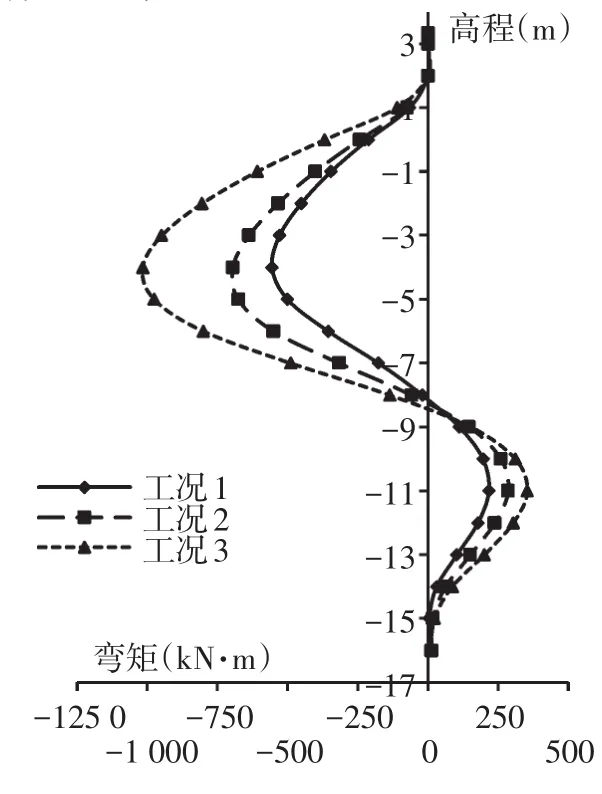
图12 主桩弯矩Fig.12 Main pile moment

图13 套板弯矩Fig.13 Inlaid sheet moment

4 主桩尺寸的影响

主桩作为主要持力构件，其尺寸的改变能对整体的工作状态和土压力的分布产生影响，下面从主桩入土深度和刚度两方面入手，探讨合理的结构尺寸。

4.1 主桩入土深度的影响

基于3种工况，研究不同主桩入土深度下的各构件弯矩变化，如图14～图19所示。

由图14～图19可知，入土深度为6 m时，主桩呈现较大刚性，在泥面以上受力较大，随入土深度的增加，主桩上部弯矩逐渐减小，下部弯矩范围有所扩大。均载施加结束后，主桩下部最大弯矩达到354.1 kN·m，约为上部最大弯矩的32%。在一定范围内，套板弯矩随主桩入土深度的增加明显增大，当主桩达到一定深度且具有较强柔性特征时，套板的受力有缓慢减小的趋势。主桩入土7 m时套板弯矩最大，其最大值约为入土6 m时的1.9倍。可见，主桩的入土深度对整体稳定性具有重要影响，主桩入土越深，结构在泥面以上的部分内力越小。

4.2 主桩刚度的影响

基于3种工况，分别选取0.6 m×1.0 m（宽×厚）、0.8 m×0.8 m和1.0 m×0.6 m的主桩截面，研究不同主桩刚度下的各构件弯矩变化，如图20～图25所示。

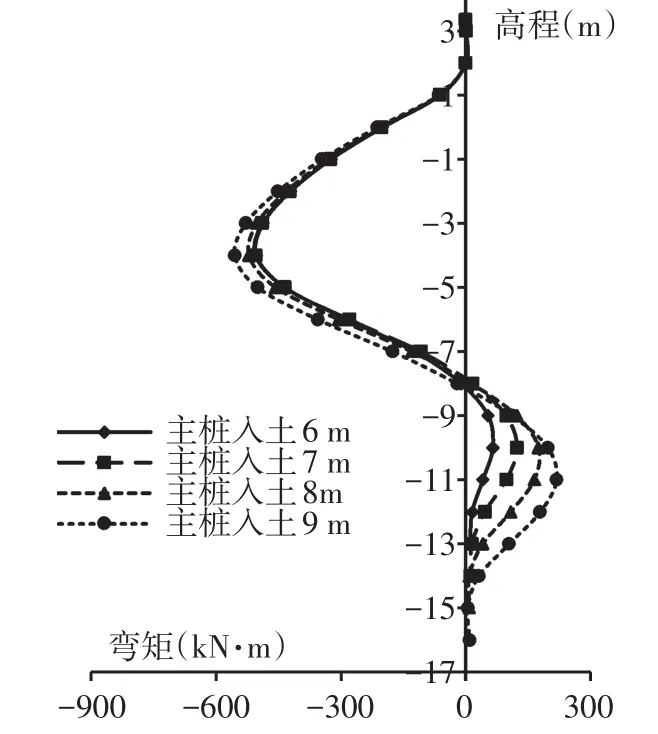
图14 主桩弯矩（工况1）Fig.14 Main pile moment（condition 1）

图15 套板弯矩（工况1）Fig.15 Inlaid sheet moment（condition 1）

图16 主桩弯矩（工况2）Fig.16 Main pile moment（condition 2）

图17 套板弯矩（工况2）Fig.17 Inlaid sheet moment（condition 2）

图18 主桩弯矩（工况3）Fig.18 Main pile moment（condition 3）

图19 套板弯矩（工况3）Fig.19 Inlaid sheet moment（condition 3）

图20 主桩弯矩（工况1）Fig.20 Main pile moment（condition 1）

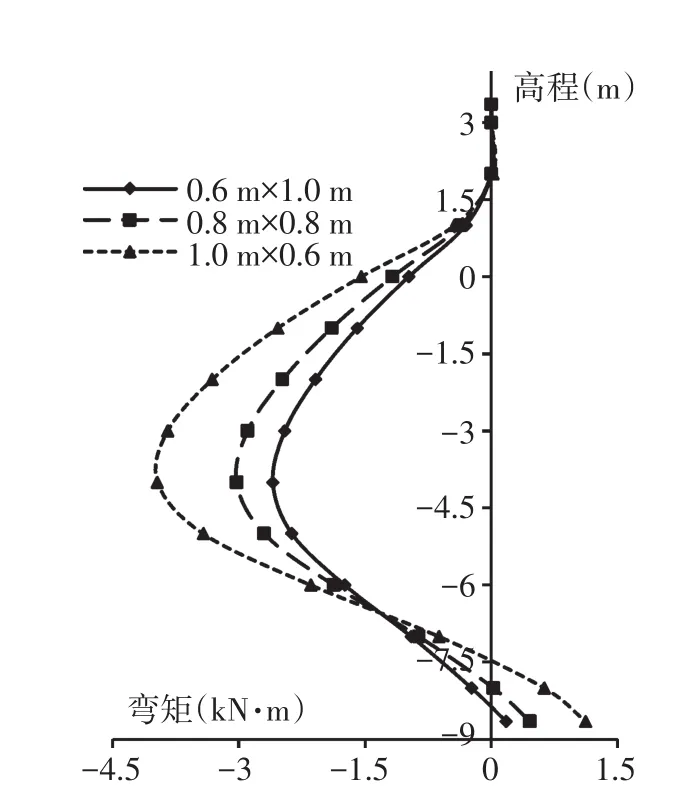
图21 套板弯矩（工况1）Fig.21 Inlaid sheet moment（condition 1）

图22 主桩弯矩（工况2）Fig.22 Main pile moment（condition 2）

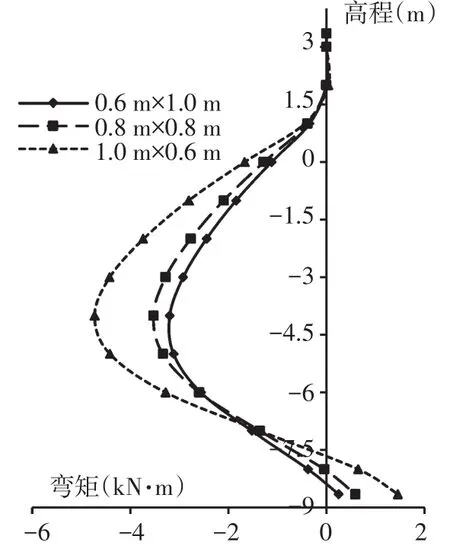
图23 套板弯矩（工况2）Fig.23 Inlaid sheet moment（condition 2）

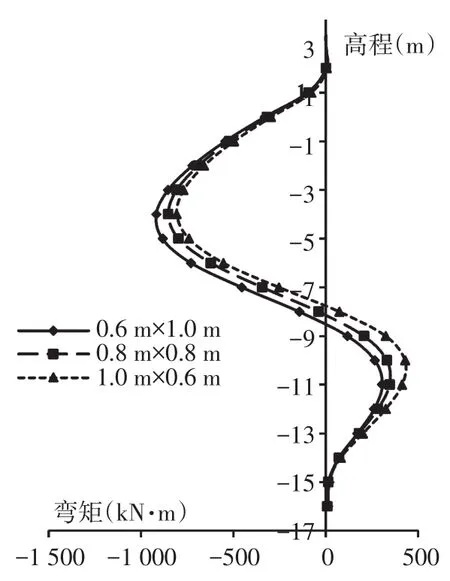
图24 主桩弯矩（工况3）Fig.24 Main pile moment（condition 3）

图25 套板弯矩（工况3）Fig.25 Inlaid sheet moment（condition 3）

由图20～图25可知，随主桩宽厚比的增加，主桩上部弯矩逐渐减小，下部弯矩逐渐增大，稳定性有所提升。与主桩相反，套板的受力逐渐增大，均载施加结束后，主桩截面1.0 m×0.6 m对应的套板最大弯矩约为0.6 m×1.0 m的1.5倍。套板尺寸一定时，主桩宽厚比的减小将导致桩板相对刚度比的加大，促使结构背侧的土拱效应［9］发挥，有更多的土压力作用在主桩上，从而减小了套板的受力。可以看出，主桩截面型式的改变所引起土压力分配情况的改变，对套板影响较大，实际工程中可通过加大主桩刚度的方式减小套板受力。

5 结论

本文参考京唐港地质资料，推导主桩、套板入土深度与桩板宽度比的关系式，分别采用传统m法和考虑锚碇点位移的m法对主桩进行计算，并与有限元结果对比；基于ABAQUS建立三维桩土模型，研究不同工况下主桩套板结构的受力特点，探讨主桩尺寸对套板内力的影响，得到以下主要结论：

（1）考虑锚碇点位移的m法与有限元法的计算结果相近，前者得到的泥面下桩身最大弯矩约为后者的0.9倍，设计主桩套板结构时不能忽略锚碇点位移的影响。

（2）主桩承担了大部分土压力，由于上下两端固定，在泥面以上的跨中部位产生较大弯矩，同时在泥面下一定深度范围内产生反向弯矩；由于刚度较小的缘故，套板的变形比主桩大很多。

（3）主桩入土深度能对结构稳定性产生影响。主桩入土较浅时属于刚性短桩，在泥面以上产生较大弯矩；随入土深度的增加主桩下部弯矩明显提高，套板的弯矩逐渐增大并最终趋于稳定。

（4）主桩刚度能对结构背侧的土压力分配产生影响。随主桩宽厚比的增加，有越来越多的土压力作用在主桩上，促使上部弯矩增大。主桩刚度的增加能够减小套板的受力，为节省材料套板厚度可以适当减小。

［1］韩理安.港口水工建筑物：第二版［M］.北京：人民交通出版社，2010.

［2］陈达，杜辰，廖迎娣.主桩套板结构受力特性研究［J］.水运工程，2014（6）：136-141. CHEN D，DU C，LIAO Y D.Mechanical behaviors of main pile with inlaid sheet structure［J］.Port&Waterway Engineering，2014，（6）：136-141.

［3］李海光.新型支挡结构设计与工程实例［M］.北京：人民交通出版社，2004.

［4］JTS 167-3-2009，板桩码头设计与施工规范［S］.

［5］戴自航，陈林靖.多层地基中水平荷载桩计算m法的两种数值解［J］.岩土工程学报，2007，29（5）：690-696. DAI Z H，CHEN L J.Two numerical solutions of laterally loaded piles installed in multi⁃layered soils by m method［J］.ChineseJournal of Geotechnical Engineering，2007，29（5）：690-696.

［6］莫海鸿，杨小平.基础工程：第二版［M］.北京：中国建筑工业出版社，2008.

［7］范文田.地下墙柱静力计算［M］.北京：人民铁道出版社，1978.

［8］费康，张建伟.ABAQUS在岩土工程中的应用［M］.北京：中国水利水电出版社，2010.

［9］杜辰.主桩套板结构力学特性及设计方法研究［D］.南京：河海大学，2014.

天津今年将投160亿元支撑天津港承接自贸区

本刊从天津港集团获悉，围绕10万t级大沽沙航道、高沙岭港区10万t级航道等一系列港口基础建设，天津2015年将投入160亿元，支撑天津港承接自贸区、“一带一路”建设等国家重大战略。获批的天津自贸区范围包括天津港片区30 km2。2015年，天津市将力争年内确保天津港圣瀚石化码头、南疆中部散货堆场、大港港区10到12号化工码头和10万t级大沽沙航道等工程完工。与此同时，今年还将新开工天津港高沙岭港区10万t级航道一期、中国石化天津液化天然气码头、南疆港区27＃通用泊位、临港经济区南部区域新兴建材产业基地通用码头等工程。（殷缶，梅深）

中国和阿联酋联合承接埃及港口建设开发

据报道，埃及交通部与阿联酋Al⁃Suwaidi集团在埃及经济发展大会(13日至15日在西奈半岛南部城市沙姆沙伊赫召开)期间签署了一项价值60亿美元的合同。根据合同，Al⁃Suwaidi集团将负责投资埃及Ain Sokh⁃na港和Damietta港的进一步开发。合同还同时规定，中国港湾建设集团将作为主要承包商和运营商参与上述两个港口的建设。埃及交通部长表示，促进物流和交通领域的建设和投资是埃及政府当前的重要任务之一。他还透露，埃及政府将大力投资东部港口，以支持苏伊士运河的扩张。（殷缶，梅深）

Simplified calculation and optimal design of main pile with inlaid sheet structure

DU Chen1,GUAN Xue⁃peng1,LIU Xian⁃peng2,LIU Hong⁃biao2
（1.Tianjin Port Business Facilities Management Centre,Tianjin 300456,China;2.Tianjin Research Institute for Water Transport Engineering,Tianjin 300456,China）

Main pile with inlaid sheet structure is a kind of sheet⁃pile structure,whose calculation theory and design method remains unclear.Combined with a project case,a simplified calculation method was put forward in the paper,and relationship among main pile embedded depth,inlaid sheet embedded depth as well as width ratio between pile and sheet was formulated.Meanwhile,conventional m method and m method considering anchored point displacement were both utilized to calculate internal force of main pile,whose results were compared with those of finite element method.Based on ABAQUS,a 3D pile⁃soil model was built to study mechanical properties of the structure under different working conditions,and analysis was made about impacts of main pile embedded depth and rigidity on internal force of inlaid sheet.It is revealed that the anchored point displacement shouldn′t be ig⁃nored,and main pile embedded depth will reduce when inlaid sheet gets narrower and deeper.Main pile embedded depth has influence on the overall stability of structure,and internal force of inlaid sheet tends to be stable with the increase of main pile depth.Besides,increasing main pile rigidity helps reduce the stress of inlaid sheet.In order to save material,inlaid sheet could be made thinner appropriately.

sheet⁃pile structure;main pile with inlaid sheet structure;m method;ABAQUS

TV 331

A

1005-8443（2015）02-0145-08

2014-08-22；

2014-10-14

杜辰（1989-），男，山东省临沂人，助理工程师，主要从事港口工程结构研究。Biography：DU Chen（1989-），male，assistant engineer.