基于LOD-FDTD的微带线边缘奇异性处理技术研究

李 磊张 昕孙亚秀

①(哈尔滨工程大学信息与通信工程学院 哈尔滨 150001)

②(五邑大学信息工程学院 江门 529020)

基于LOD-FDTD的微带线边缘奇异性处理技术研究

李 磊*①张 昕①②孙亚秀①

①(哈尔滨工程大学信息与通信工程学院 哈尔滨 150001)

②(五邑大学信息工程学院 江门 529020)

为解决现有方法在处理微带线边缘电磁场的奇异性时，存在计算效率和精度之间的矛盾，该文提出一种在局部1维时域有限差分法(LOD-FDTD)基础上，结合微带线边缘电磁场分布函数，并通过坐标变换可处理导体嵌入网格面积大于1/2时的情况，因而适用性更广的微带线边缘奇异性处理技术。与现有奇异性处理技术对比证明，该算法在采用的时间步长小于等于Courant-Friedrichs-Lewy(CFL)稳定性条件所允许最大时间步长5倍的情况下，具有更高的计算精度。且与一般LOD-FDTD算法对比证明，引入的微带线边缘电磁场分布函数使得该算法在节省计算资源和提高计算效率的同时，保持了更高的计算精度。

微带线；局部1维时域有限差分法；奇异性处理；坐标变换

1 引言

近些年来，时域有限差分法(Finite Difference Time Domain, FDTD)作为一种直接求解麦克斯韦(Maxwell)微分方程的时域方法，由于具有物理含义清晰，易于实现等优点，被应用于各类电磁仿真问题。然而，在解决具有微带结构的问题时，由于微带线通常具有较窄宽度以及导体边缘电磁场具有奇异性[1]等问题，使得传统FDTD方法不得不采用较小的空间网格尺寸才能准确描述微带线边缘剧烈变化的电磁场，而且由于Courant-Friedrichs-Lewy (CFL)稳定性条件的限制，较小的空间网格尺寸将导致较小的时间步长，从而使得传统FDTD方法在计算微带结构需占用很大的计算资源，且计算效率很低。

为解决上述问题，文献[2]提出亚网格方法，在微带线边缘电磁场变化剧烈处采用小尺寸网格，在电磁场变化平缓处采用大尺寸网格，从而使得计算网格数量大大减少，节省了计算资源，但该方法的时间步长是由最小空间网格尺寸决定的，因此在计算时间上并无较大改善；文献[3]提出修改材料电参数(Modified Assigned Material Parameters, MAMPs)的方法，在不减小空间网格尺寸的同时，保证了算法具有较高的精度，但该方法对导体嵌入网格面积大于1/2时的情况没有办法处理，且时间步长仍受到CFL稳定条件的限制。由此可见，CFL条件的限制是利用FDTD解决微带结构问题面临的主要挑战。而以Crank Nicolson(CN)-FDTD[4-7]，交替方向隐式(Alternating Direction Implicit, ADI)-FDTD[8-11]和局部1维(Locally One-Dimensional, LOD)-FDTD[12-15]为代表的无条件稳定的隐式FDTD方法正是解决上述问题的关键，特别是LOD-FDTD方法，更是具有实现简单和计算效率高等优点。然而隐式FDTD方法虽然是无条件稳定的，但如果采用时间步长与空间网格尺寸的比值远大于CFL条件的限制，则会产生较严重的数值色散，从而降低计算精度。

为了克服以上问题，本文提出了一种在LOD-FDTD的基础上，结合了文献[16]提出的微带线边缘电磁场分布函数，并通过坐标变换可处理导体嵌入网格面积大于1/2时的情况，因而适用性更广的微带线边缘奇异性处理技术，该方法保证了较小的时间步长与空间网格尺寸的比值，从而减小了数值色散，且在具有较高计算效率的同时，保持了较高的计算精度。

本文组织如下：首先通过理论推导出基于LOD-FDTD的微带线边缘电磁场更新方程；然后分别通过本文算法与亚网格算法、MAMPs算法，本文算法与不同网格划分方式的一般LOD-FDTD方法，以及本文算法采用不同时间步长的计算结果对比，从而验证算法的性能；最后对全文进行总结。

2 基于LOD-FDTD的微带线边缘奇异性处理技术

2.1 微带线边缘场分布函数

由于微带线边缘的电磁场具有奇异性，因而在建模时需要特别处理，否则会导致局部的截断误差。根据微带线边缘场分布函数，如图1所示的微带线边缘电磁场可表示为

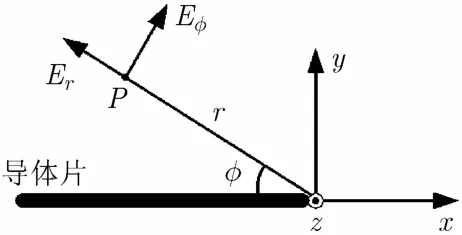
图1 微带线边缘横向电磁场

式中r为微带线边缘到场点的距离，φ为二者之间的夹角，A和B为未知系数。由式(1)～式(4)可见，由于1/项的存在使得横向场Er和Eφ具有奇异性。

2.2 基于LOD-FDTD的微带线边缘电磁场计算方法

现以图2和图3中的Hy(i,j,k)和Ez(i+1,j,k)为例，说明本文提出的具有奇异性的微带线边缘电磁场计算方法。由图2可见，s为导体嵌入网格长度，Δx, Δy, Δz分别为x, y, z方向的空间网格尺寸，i, j, k分别为x, y, z方向的网格坐标，令s＞Δx/2(对于s≤Δx/2情况可按类似方法处理)。如果按照传统Yee网格划分方式，则Ex(i,j,k), Ex(i,j,k+1)和Hy(i,j,k)均为零，这相当于增大了导体嵌入网格的长度，将导致计算误差，因而本算法将Ex(i,j,k), Ex(i,j,k+1)和Hy(i,j,k)3个节点的坐标沿 x 轴移动s/2，以使得算法可以准确表示微带线边缘的场。此时r=(Δx-s )/2, φ=180o，因而Hy(i,j,k)=-Hφ, Ex(i,j,k)=Er，由式(1)和式(4)可得

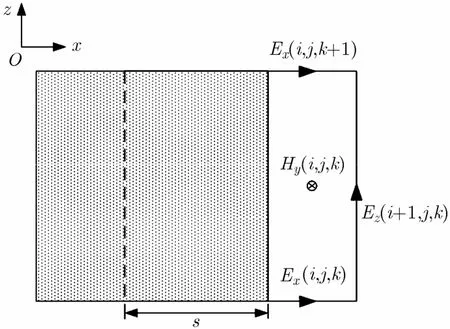
图2 微带线嵌入网格xOz平面图

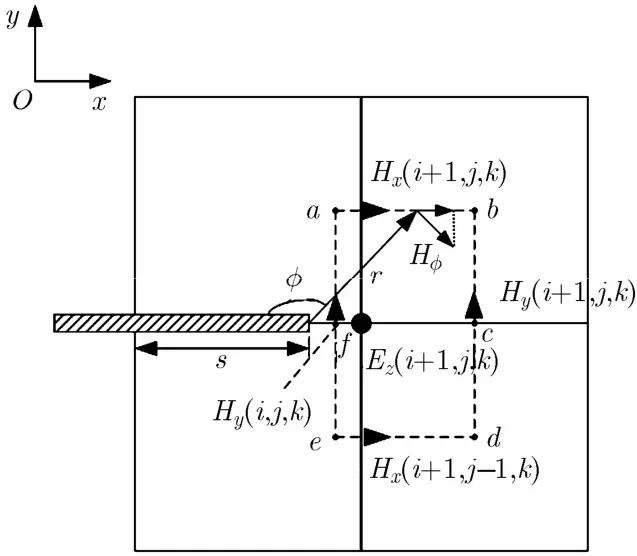
图3 微带线嵌入网格xOy平面图

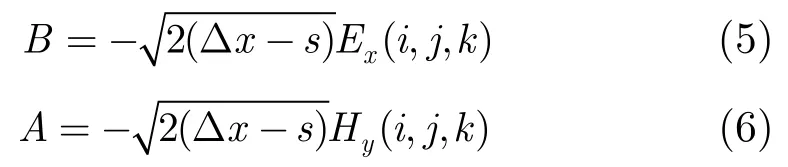
将式(5)和式(6)分别代入式(1)和式(4)可得导体边缘横向场的分布为

根据类似方法，图3中的磁场xH和yH为横向场，按照夹角φ的变化可将其分为ab, bc, cd, de, ef, fa 6段，表示为

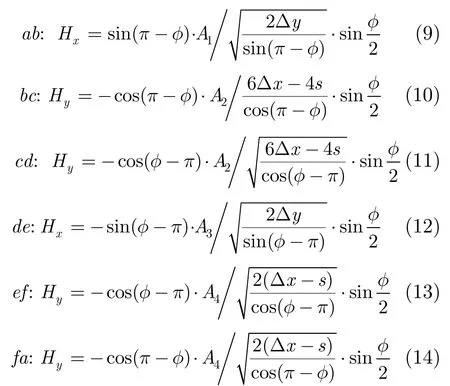
式中，

在求得微带线边缘电磁场的分布表达式后，算法虽然可不减小网格尺寸就能准确描述微带线边缘电磁场，但计算效率仍旧受到CFL稳定条件限制。为了突破CFL稳定条件对计算效率的限制，可将无条件稳定的隐式方法LOD-FDTD与其结合。但传统LOD-FDTD由于分裂矩阵因子具有不可交换性，使得其只有一阶时间精度。因此本文采用了可消除二阶不可交换性误差，从而具有二阶时间精度的LOD-FDTD算法。该算法更新方程可表示为

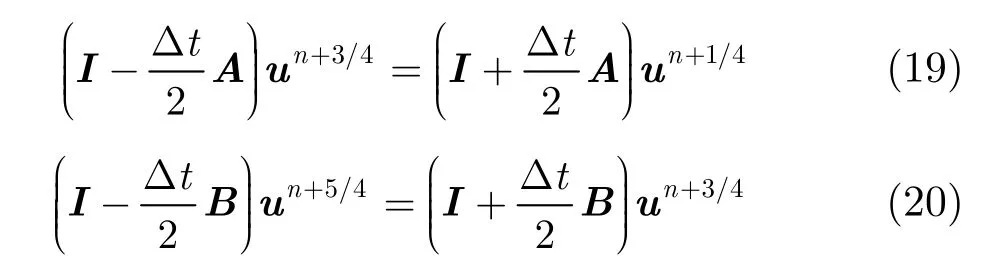
式中，

下面结合上述LOD-FDTD算法得到基于LOD-FDTD的微带线边缘奇异性处理技术。受篇幅限制，这里只介绍对微带线边缘电场Ez(i+1,j,k)和磁场Hy(i,j,k)的计算方法，其他场量可按类似方法求得。本文算法将时间的推进分为(n+1/4)到(n+3/4)和(n+3/4)到(n+5/4)两个子时间步。

首先，前半时间步(n+1/4)到(n+3/4)的微带线边缘电场Ez(i+1,j,k)更新方程可由安培定律得到。

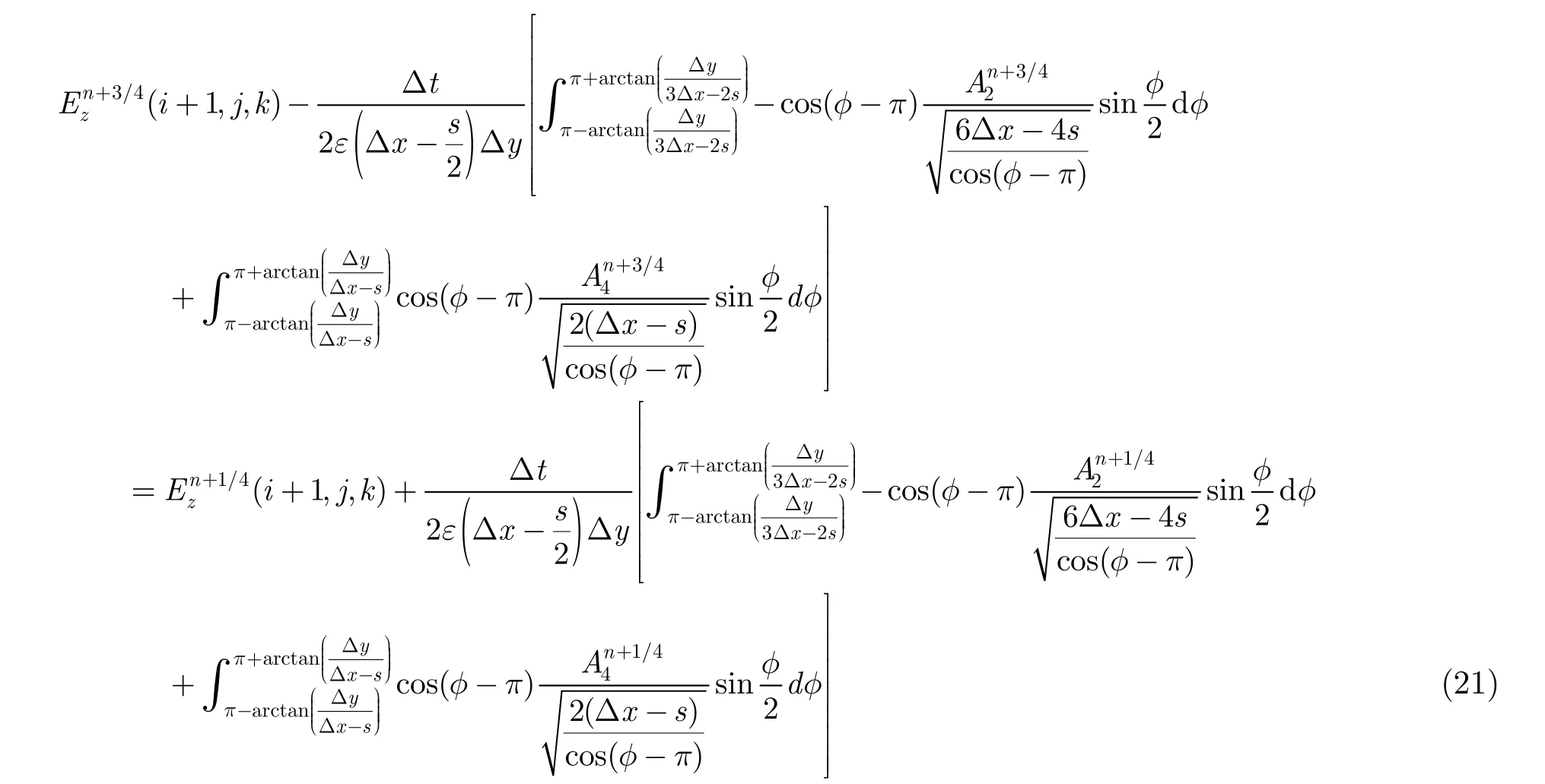
式中，Δt为时间步长，ε为介电常数。

磁场Hy(i,j,k)更新方程可由法拉第定律得到。

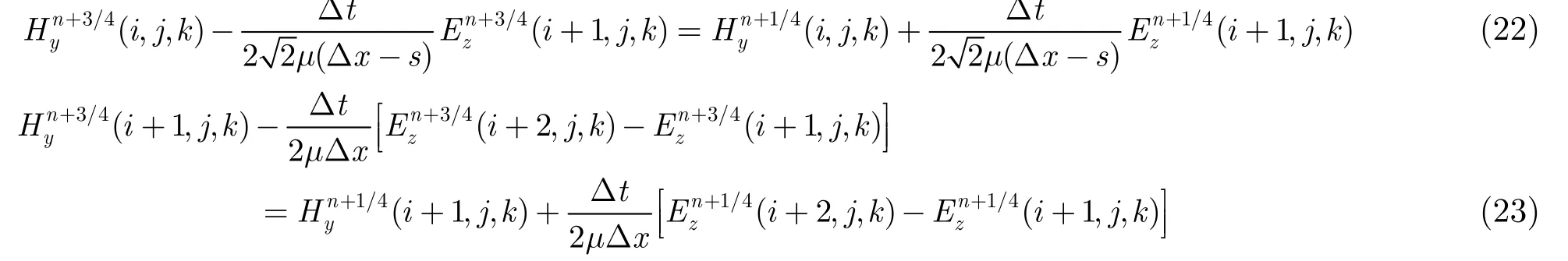
式中，μ为磁导率。

将式(16)、 式(18)、 式(22)和式(23)代入式(21)，整理后得

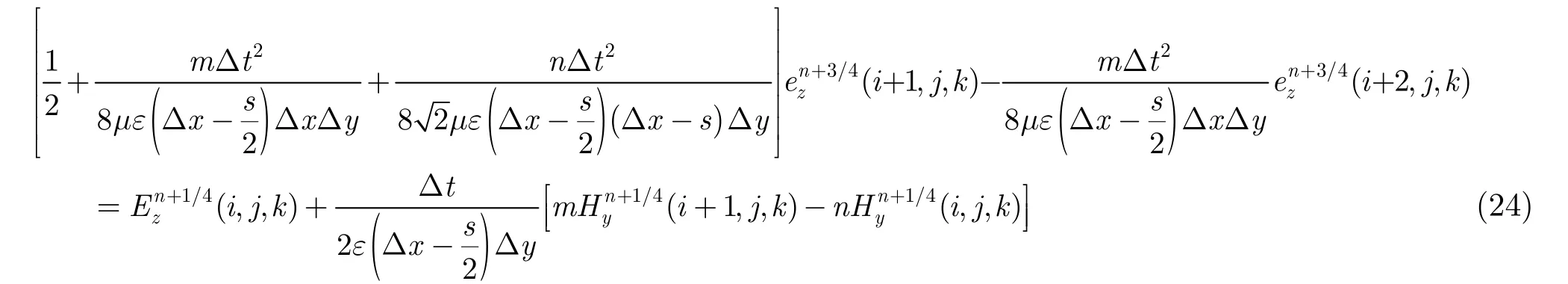
式中，

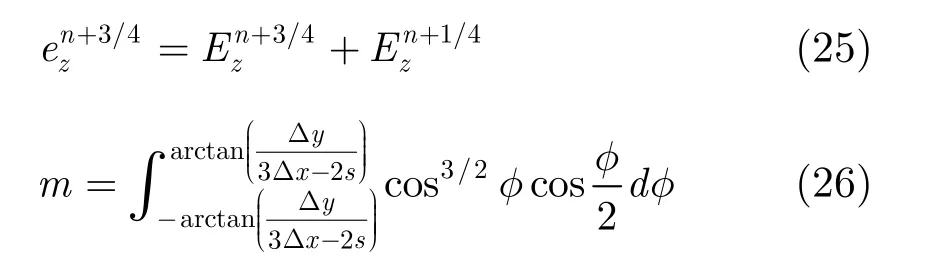
同理，后半时间步(n+3/4)到(n+5/4)的微带线边缘电场更新方程整理后为

式中，

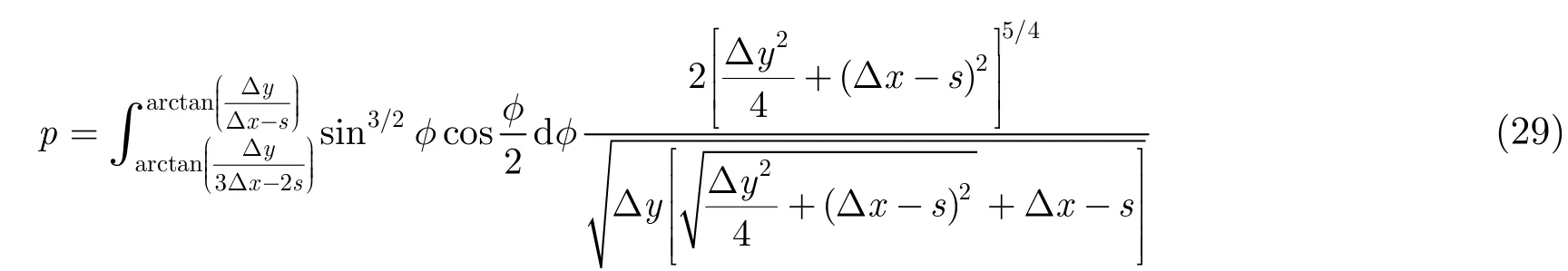
磁场Hy(i,j,k)更新方程为

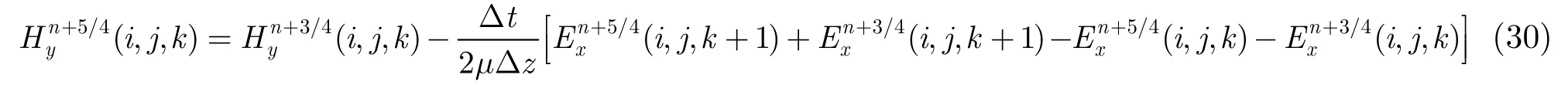
通过观察上述更新方程可知，待定系数m, n和p不随时间变化，因此只需在算法迭代开始时计算1次即可，从而不影响计算效率。

3 算法检验

为了验证本文算法的准确性，分别利用本文算法、亚网格算法和MAMPs算法计算相对介电常数εr=1，厚度h=1.27 mm 的介质板上不同宽度微带线的特性阻抗，并与理论值进行对比，如图4所示。其中本文算法和MAMPs算法在整个计算空间采用Δx=Δy =1 mm, Δz=0.3175 mm 的网格划分；同时根据亚网格算法原理，为保证计算精度，亚网格算法在微带线边缘电磁场变化剧烈处采用Δx=Δy=0.25 mm的较小网格划分，而在电磁场变换平缓的其他位置采用Δx=Δy=1 mm的网格划分以保证一定的计算效率，3种算法的时间步长均采用满足CFL条件要求的最大值。

3.1 本文算法与已有算法的对比

由图4可知，3种算法中，本文算法计算结果与理论值的平均误差最小，约为0.85%, MAMPs算法居中，约为2.57%，亚网格算法最大，约为8.35%，且其计算时间也大于本文和MAMPs算法的计算时间。由图4还可见，采用相同网格划分方式的本文与MAMPs算法都是在微带线宽度为0.05 mm时，与理论值的误差最大，其中本文算法的误差约为1.47%，而MAMPs算法的误差约为8.98%；随着微带线宽度增加，即导体嵌入网格面积的增大，误差逐渐减小，当导体嵌入面积约为网格面积的1/4时，两种算法的计算结果与理论值的误差最小，均约为0.018%，之后随着导体嵌入面积的近一步增大，误差又逐渐增大。由此可见，相比于亚网格和MAMPs算法，本文算法具有较高的计算精度；且为保证算法的准确性，最好在建模时，使得导体嵌入网格面积约为网格面积的1/4。

3.2 本文算法与一般LOD-FDTD算法对比

为了检验本文引入的微带线边缘奇异性处理技术对LOD-FDTD方法计算精度的改善情况，分别采取Δx=Δy =1mm, Δz =0.3175 mm的网格划分且CFLN=5的本文算法和采取相同空间网格划分但CFLN=1的粗网格一般LOD-FDTD算法，以及采取Δx=Δy=0.2mm, Δz =0.1588 mm且CFLN=1, 5, 10的细网格一般LOD-FDTD算法计算相对介电常数εr=1，厚度h=1.27 mm 的介质板上宽度为0.05～0.9 mm微带线的特性阻抗，结果如图5所示，其中定义CFLN为算法所采用的时间步长与CFL条件所允许最大时间步长的比值。

由图5可见，本文算法在CFLN=5时的计算结果与理论值的平均误差为1.57%，采用细网格的一般LOD-FDTD方法在CFLN=1, 5, 10时计算结果的平均误差分别为5.89%, 6.54%, 7.40%，而采用了粗网格的一般LOD-FDTD方法的计算结果平均误差最大，约为63.46%。且微带线的宽度变化只要不超过网格尺寸，一般LOD-FDTD方法是无法分辨的，以致于在某些微带线宽度上与理论值相比具有很大的计算误差。由此可见，相比于一般LOD-FDTD算法，引入的微带线边缘奇异性处理技术使得本文算法在采用较大网格划分方式，从而节省了计算资源和提高了计算效率的同时，保持了较高的计算精度。

3.3 不同时间步长的计算精度对比

为了检验本文算法在导体嵌入网格面积大于1/2时的适用性，以及算法所采用的时间步长与CFL条件所允许最大时间步长的比值对计算精度的影响，利用本文算法，并采用与计算图4时相同的网格划分，计算相对介电常数εr=1，厚度h=1.27mm的介质板上宽度为0.05～1.80 mm微带线的特性阻抗，如图6所示。

由图6可见，当导体嵌入网格面积大于1/2时，本文算法计算结果与理论值仍保持了较好的一致性，其中CFLN=1, 5, 10时的平均误差分别约为0.97%, 1.73%, 3.97%。且由图6还可见，导体嵌入网格面积约为网格面积的1/20时，CFLN=1, 5, 10的计算误差分别约为1.47%, 2.87%, 4.33%；随着嵌入面积的增大，计算误差逐渐减小，当约为网格面积的1/4时，计算误差均小于1%；之后随着嵌入面积的近一步增大，CFLN=1, 5的计算误差虽有一定增大，但仍小于2%，而CFLN=10的计算误差则增大较多，特别是当嵌入面积大于网格面积的1/2，计算误差均大于5%。因而通过与图4中亚网格算法、MAMPs算法的计算结果对比可知，除可解决导体嵌入网格面积大于1/2时的情况，本文算法在CFLN≤5，即计算效率最大可提高约5倍时，受数值色散的影响较小，算法仍具有更高的计算精度，而CFLN=10时，数值色散对计算精度产生了较大影响，特别是导体嵌入面积大于网格面积的1/2时，计算精度下降较快，略低于亚网格算法。

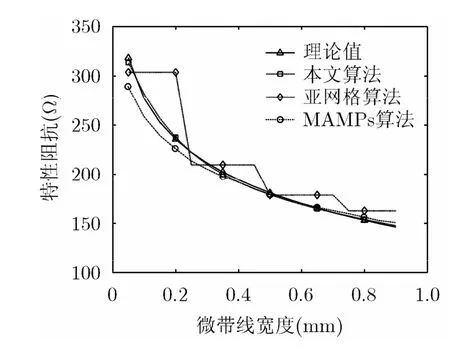
图4 不同算法计算结果对比

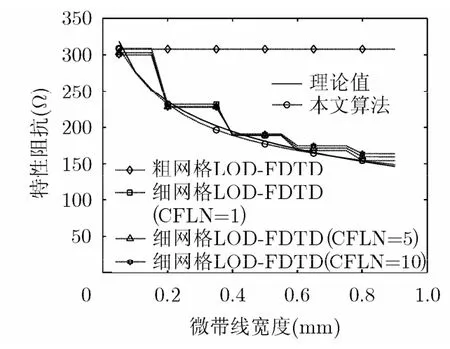
图5 本文算法与一般LOD-FDTD计算结果对比

图6 不同CFLN的计算结果对比

4 结束语

为了解决现有方法在处理微带线边缘电磁场的奇异性时，存在计算效率和计算精度之间的矛盾，本文提出了一种在LOD-FDTD基础上，结合微带线边缘电磁场分布函数，并通过坐标变换可处理导体嵌入网格面积大于1/2时的情况，因而适用性更广，计算资源更节省，计算效率和计算精度更高的微带线边缘奇异性处理技术。通过实验证明，本文算法在采用的时间步长小于等于CFL条件所允许最大时间步长的5倍时，相比于现有的亚网格算法和MAMPs算法，在保持更高计算效率的同时，具有更高的计算精度，且导体嵌入网格面积约为网格面积的1/4时，计算精度达到最高；相比于一般的LOD-FDTD方法，引入的微带线边缘电磁场分布函数使得本文算法在节省了计算资源并提高了计算效率的同时，保持了较高的计算精度。但当本文算法采用的时间步长等于CFL条件所允许最大时间步长的10倍时，数值色散对计算精度产生了较大影响，使得计算精度下降较快，因而克服大于CFL条件允许的10倍时间步长引起的数值色散对计算精度的影响是下一步研究的重点。

[1] Mur G. The modeling of singularities in the finite-difference approximation of the time-domain electromagnetic-fields equations[J]. IEEE Transactions on Microwave Theoey and Technology, 1981, 29(10): 1073-1077.

[2] Taflove A. The Finite-Difference Time-Domain Method [M]. Boston: Artech House, 1995: 190-216.

[3] Railton J and Paul L. Analysis of structures containing sharp oblique metal edges in FDTD using MAMPs[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(9): 2954-2959.

[4] 王为, 周东明, 刘培国, 等. 端接任意负载传输线的分步CN-FDTD分析方法[J]. 电子与信息学报, 2013, 35(1): 209-214.

Wang Wei, Zhou Dong-ming, Liu Pei-guo, et al.. Transient analysis of transmission line with arbitrary loads based on the split-step Crank-Nicolson-FDTD method[J]. Journal of Electronics & Information Technology, 2013, 35(1): 209-214.

[5] Kim H, Koh S, and Yook J G. Implicit ID-FDTD algorithm based on Crank-Nicolson scheme: dispersion relation and stability analysis[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(6): 2259-2267.

[6] Rouf H K, Costen F, and Fujii M. Modeling EM wave interactions with human body in frequency dependent Crank Nicolson method[J]. Journal of Electromagnetic Waves and Applications, 2011, 25(17): 2429-2441.

[7] 金涛斌, 邹军. 快速时域有限差分方法计算矩形缺陷接地结构[J]. 电波科学学报, 2012, 27(5): 853-858.

Jin Tao-bin and Zou Jun. Calculation of transmission parameters for a rectangle defected ground structure using fast FDTD scheme[J]. Chinese Journal of Radio Science, 2012, 27(5): 853-858.

[8] Yang Shun-chuan, Chen Zhi-zhang, Yu Yi-qiang, et al.. On the divergence properties of the new efficiency-improved divergence preserved ADI-FDTD method[C]. Proceedings of the IEEE MTT-S International Microwave SymposiumDigest, Seattle, USA, 2013: 1-3.

[9] Kong Yong-dan, Chu Qing-xin, and Li Rong-lin. High-order unconditionally-stable four-step ADI-FDTD methods and numerical analysis[J]. Progress in Electromagnetic Research, 2013, 135: 713-734.

[10] Gan Theng-huat and Tan Eng-leong. Stability and dispersion analysis for three-dimensional (3-D) leapfrog ADI-FDTD method[J]. Progress in Electromagnetics Research, 2012, 23: 1-12.

[11] Yang Shun-chuan, Chen Zhi-zhang, Yu Yi-qiang, et al.. An unconditionally stable one-step arbitrary-order leapfrog ADI-FDTD method and its numerical properties[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(4): 1995-2003.

[12] 刘国胜, 张国基. 高阶LOD-FDTD 方法的数值特性研究[J].电子与信息学报, 2010, 32(6): 1384-1388.

Liu Guo-sheng and Zhang Guo-ji. Study for the numerical properties of the higher-order LOD-FDTD methods[J]. Journal of Electronics & Information Technology, 2010, 32(6): 1384-1388.

[13] Ahmed I, Khoo E H, and Li E. Efficient modeling and simulation of graphene devices with the LOD-FDTD method[J]. IEEE Microwave and Wireless Components Letters, 2013, 23(6): 306-308.

[14] Saxena K and Srivastava V. Stability and dispersion analysis of higher order unconditionally stable three-step locally one dimensional finite-difference time-domain method[J]. IET Microwaves, Antennas & Propagation, 2013, 7(12): 954-960.

[15] Gan Theng-huat and Tan Eng-leong. Unconditionally stable fundamental LOD-FDTD method with second-order temporal accuracy and complying divergence[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(5): 2630-2638.

[16] Van J. Singular Electromagnetic Fields and Sources[M]. Clarendon: IEEE Press, 1991: 125-158.

李 磊： 男，1984年生，博士生，研究方向为计算电磁学、电磁兼容、电磁场与微波技术.

张 昕： 男，1965年生，教授，博士生导师，研究方向为计算电磁学、电磁兼容、天线设计.

孙亚秀： 女，1974年生，副教授，硕士生导师，研究方向为计算电磁学、电磁兼容、电磁场与微波技术.

Study for Singularity Processing Technology of Microstrip Line Edge Based on the LOD-FDTD

Li Lei①Zhang Xin①②Sun Ya-xiu①①(School of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)
②(School of Information Engineering, Wuyi University, Jiangmen 529020, China)

In order to solve the contradiction between the efficiency and accuracy as using the existing methods in the processing of the singularity of electromagnetic field near the microstrip line edge, in this paper, a microstrip line edge singularity processing technology based on the Locally One Dimensional Finite Difference Time Domain (LOD-FDTD), and combined with distribution function of electromagnetic field near microstrip line edge is proposed. The algorithm can handle conductors embedded in the grid area of more than 1/2 by the coordinate transformation, thus having wide applicability. Compared with the existing processing technology, the proposed algorithm in this paper has higher calculation accuracy, when the time step size is less than or equal to 5 times of the Courant-Friedrichs-Lewy (CFL) condition allowed. And compared with general LOD-FDTD, the proposed algorithm by introducing distribution function of electromagnetic field near microstrip line edge not only saves the computational resources and improves the efficiency, but also maintains the higher accuracy.

Microstrip line; Locally One Dimensional Finite Difference Time Domain (LOD-FDTD); Singularity processing; Coordinate transformation

TN817; TM15

A

1009-5896(2015)03-0746-07

10.11999/JEIT140518

2014-04-22收到，2014-06-27改回

国家自然科学基金(51209055)和中央高校基本科研业务费专项资金(HEUCFR1124)资助课题

*通信作者：李磊 leericky@126.com