一种新的部分频带噪声干扰模型下的FH/MFSK系统性能分析

杜 洋董彬虹 唐 鹏 周兰林

(电子科技大学通信抗干扰技术国家级重点实验室 成都 611731)

一种新的部分频带噪声干扰模型下的FH/MFSK系统性能分析

杜 洋*董彬虹 唐 鹏 周兰林

(电子科技大学通信抗干扰技术国家级重点实验室 成都 611731)

部分频带噪声干扰(PBNJ)是一种主要的窄带干扰，它对通信系统性能的影响十分突出。该文针对F H/ MFSK系统中，传统的部分频带干扰模型的干扰带宽最小分辨率是一个跳频子带带宽(即MFSK信号的带宽)，研究了更具有实际价值的新的部分频带干扰模型，即将干扰带宽最小分辨率精确到MFSK信号带宽的1/M。该文推导了莱斯衰落信道下的误比特率(BER)公式，给出了其闭合表达式，并通过计算机仿真验证了理论推导的正确性。理论分析与仿真结果表明，M,Nh,ρ越小，传统与新PBNJ模型下FH/MFSK信号的BER性能差异就越大。

跳频通信；部分频带噪声干扰；最小干扰带宽分辨率；莱斯衰落信道

1 引言

跳频(FH)通信以其优良的抗干扰性、低截获概率和组网能力在军事和民用通信领域被广泛应用[1,2]。目前，国内外对跳频通信系统的干扰与抗干扰技术研究主要集中在部分频带噪声干扰(Partial-Band Noise Jamming, PBNJ)和多音干扰(Multi-Tone Jamming, MTJ)[3]。

PBNJ是一种主要的窄带干扰类型，它对通信系统性能的影响十分突出[4]。目前，国内外学者就通信系统在PBNJ下的各种性能进行了广泛的研究。文献[5]研究了FH/MFSK系统在PBNJ下的误比特率(Bit Error Rate, BER)性能，并推导了其理论公式。文献[6]根据FH信号与PBNJ信号之间的近似统计独立特性，在双通道接收基础上，提出了一种基于盲源分离的FH通信抗PBNJ方法。文献[7]对基于自适应增益控制的非相干FFH/BFSK扩频接收机在同时存在PBNJ和AWGN的频率非选择性慢衰落Nakagami信道下的BER性能进行了分析，推导出一重积分形式的BER准确表达式。文献[8,9]研究了FFH系统利用最大似然接收机对瑞利衰落信道下混合PBNJ与MTJ信号的BER性能的影响，并进行了理论推导与仿真分析。同时，也研究了时间与频率偏移对系统的影响。文献[10]提出利用低码率的高阶调制在PBNJ下取得高带宽效率的同时，又能保持鲁棒性。文献[10]也提出了一种估算PBNJ损失的理论分析工具，并通过仿真进行了验证。文献[11]针对常规差分跳频(Differential Frequency Hopping, DFH)系统，从多进制卷积编码结合高阶MFSK调制出发，提出了一种宽带MFSK/DFH系统模型，对其基于FFT的接收机在AWGN信道中存在PBNJ条件下的BER性能进行了理论分析与仿真验证。文献[12]对DFH系统在莱斯衰落信道下的抗PBNJ性能进行了分析，推导了BER理论上界，并通过仿真验证了数值结果的合理性。文献[13]为了提高多频段多进制频移键控(MultiBand M-ary Frequency Shift Keying, MB-MFSK) 系统在PBNJ下的性能，提出了宽间隔MB-MFSK系统使同一子频段的子信道相距一定的间隔。当信号受到部分频带噪声干扰时，这种宽间隔载波映射方法可以将某一子频段受到干扰的影响分散到其它子频段上，进一步对每个子频段采用纠错编码技术，可以减小PBNJ对MB-MFSK系统性能的影响。

然而，现有涉及到跳频系统的PBNJ的研究都是基于干扰带宽最小分辨率为跳频子带带宽的传统PBNJ模型展开的。在实际干扰环境中，这种传统PBNJ模型并不总是合理。因此，文献[14]针对FH/ MFSK系统，提出了干扰带宽最小分辨率精确到MFSK信号带宽的1/M的新PBNJ模型。

本文将无线信道建模为莱斯衰落信道，推导出了FH/MFSK信号在新PBNJ模型下的BER闭合表达式，并通过计算机仿真验证了理论分析的正确性。

本文内容安排如下：第2节是传统与新PBNJ模型的对比；第3节是新PBNJ模型下FH/MFSK信号的BER分析；第4节给出数值及仿真结果对比；最后总结全文。

2 PBNJ模型

图1为FH/MFSK系统发射机和接收机的框图。在发射机，PN序列发生器产生跳频序列，控制频率合成器生成跳频频率，输入信息经MFSK调制后与跳频频率混频后产生FH/MFSK信号。最后FH/MFSK信号被调制到射频并从天线发射出去，在无线信道环境中将受到部分频带噪声干扰。

在接收机中，首先对接收到叠加干扰的宽射频信号进行射频处理，然后与发射机同步跳变的PN序列控制频率合成器对中频信号进行跳频解调。最后，经MFSK解调，恢复成原始信息输出。

设传统PBNJ模型的干扰带宽最小分辨率为WJmin1，新PBNJ模型的干扰带宽最小分辨率为WJmin2。故分别定义WJmin1=MΔf与WJmin2=Δf, Δf 是MFSK信号相邻频率间隔，M是MFSK调制阶数。

由传统与新PBNJ模型各自干扰带宽最小分辨率的定义可以得出，新PBNJ模型的干扰带宽最小分辨率是传统PBNJ模型的干扰带宽最小分辨率的1/M，即

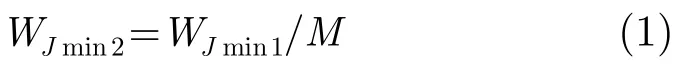
因此，新PBNJ模型具有更高的精度，更符合实际的干扰环境。传统与新PBNJ模型的对比如图2所示。

从图2(a)可以看到传统PBNJ模型下，WJ1= NWMFSK(WMFSK=MΔf为MFSK信号带宽，即跳频子带带宽；N =1,2,…,Nh, Nh是跳频频率集点数，即载波频率数)，故跳频信号存在2种状态：

(1)状态1：跳频信号未跳进PBNJ，信号未受到干扰；

(2)状态2：跳频信号跳进PBNJ，信号受到干扰。

从图2(b)可以看到，新PBNJ模型中，干扰带宽有2种类型WJ1=NWMFSK和WJ2＜WMFSK(或WJ3＜WMFSK)。当WJ2＜WMFSK(或WJ3＜WMFSK)时，跳频信号受干扰的状态又增加了2种，即：

(3)状态3：跳频信号跳进PBNJ，信号受到干扰；

(4)状态4：跳频信号未跳进PBNJ，信号未受到干扰。

定义一个随机变量Z，代表跳频信号每个码元时间间隔内的干扰状态参数。Z=1,2,3,4分别对应状态1，状态2，状态3，状态4。

图1 FH/MFSK系统框图

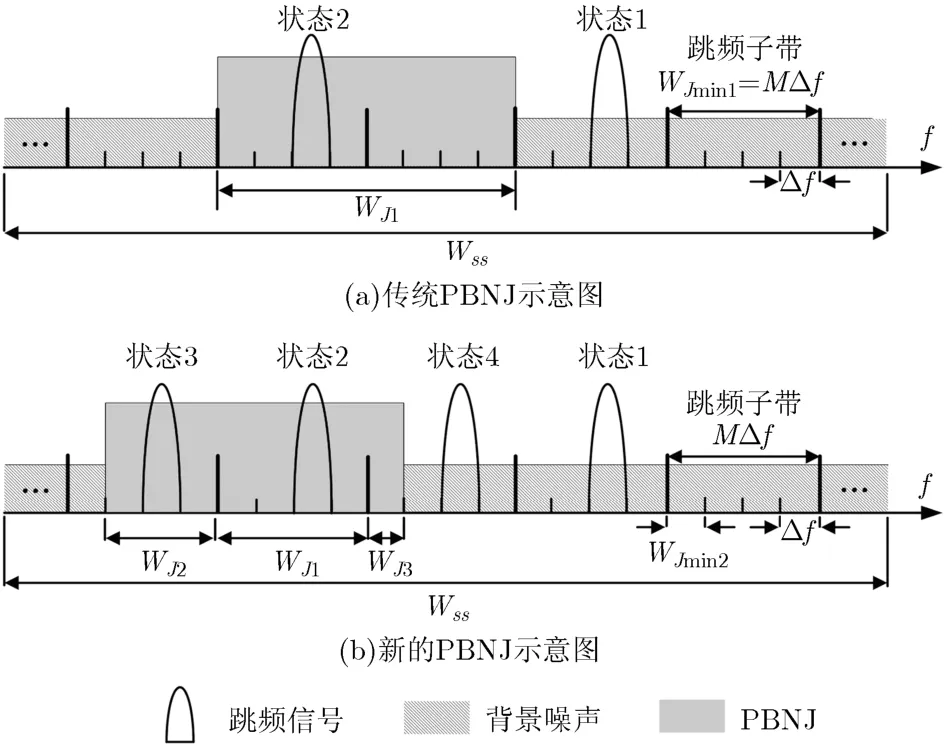
图2 传统与新PBNJ模型对比图

设新的PBNJ模型的干扰带宽为

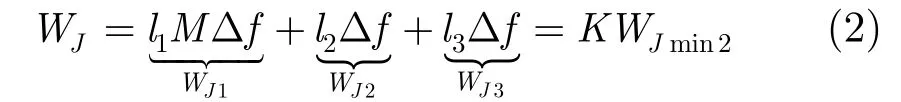
定义概率因子ijρ,i代表干扰带宽类型JiW，如图2(b)所示，其中=1,2,3i。j代表跳频信号是否跳进PBNJ，其中=1,2j(1代表跳进，2代表未跳进)。因此，

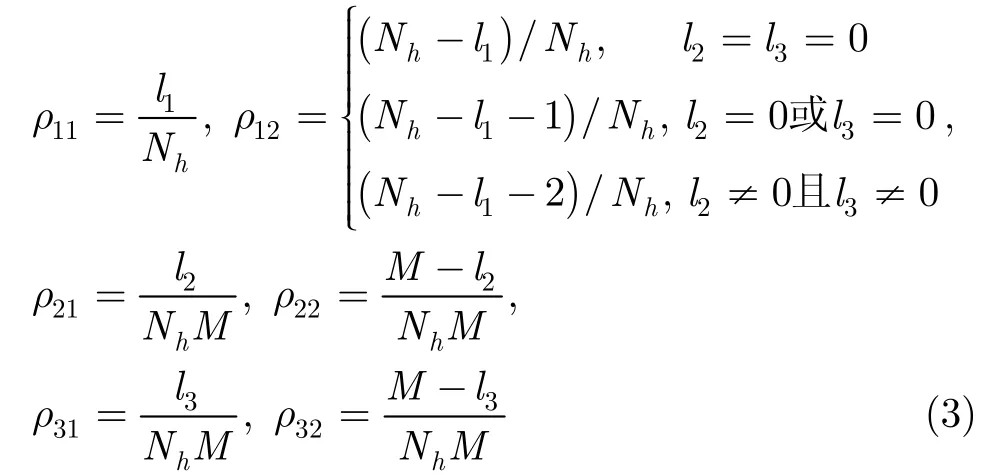
因此，概率分布式为

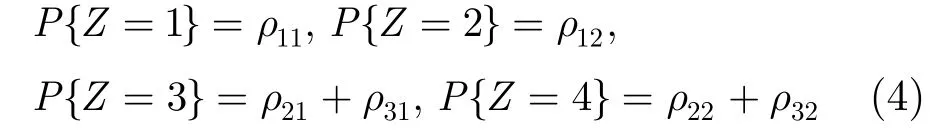
由式(2)和式(4)，可以得到新PBNJ模型下的干扰因子为

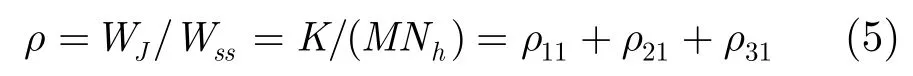
3 BER性能分析

信号sm(t)经过莱斯(Rice)衰落信道，并受到PBNJ干扰，等效低通接收信号为

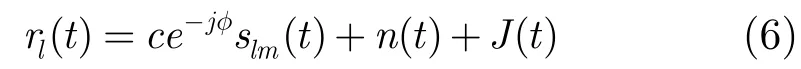
式中，slm(t)是发送信号sm(t)的等效低通信号，m=1,2,…,M 。c=a+αe-jθ表示莱斯衰落过程，其中a是信号传输直接路径的镜像分量，α是瑞利衰落分量，二阶矩E(α2)=2σ2，定义信号直射功率与散射功率之比为莱斯因子，即k=a2/2σ2。当k=0时，信号传输只存在瑞利衰落分量，莱斯衰落信道蜕化为瑞利衰落信道；当k=∞时，信号传输只存在直接路径分量，此时莱斯衰落信道蜕化为高斯信道。定义平均信噪比为(假设(1+k)⋅2σ2=1，得到，则散射路径等效平均信噪比,εs是信号能量。φl和θ表示等效低通衰落信号的相位，在[0,2π]上均匀分布。n(t)表示高斯白噪声。J(t)表示部分频带干扰噪声。

假设FH/MFSK系统发送信号为s1(t)，则相应平方律检波器输出为U1，且服从自由度为2的非中心χ2分布[15]，其概率密度函数为

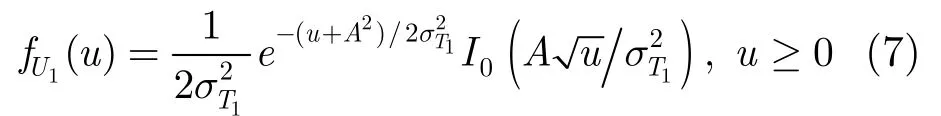
其余M-1个平方律检波器的输出Ui(i=2, 3,…,M)为噪声，也服从自由度为2的非中心χ2分布[15]，其概率密度函数为

正确判决概率是U1＞U2,U1＞U3,…,U1＞UM的概率，故错误判决概率计算公式为

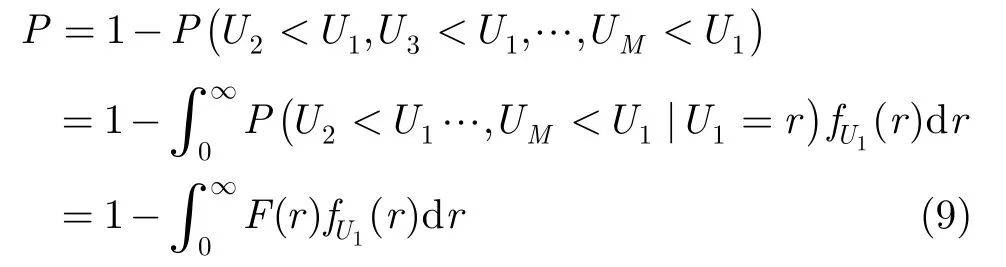
因为随机变量Ui(i=2,3,…,M)是相互统计独立的，所以F(r)的联合概率为因式分解M-1项的乘积。令

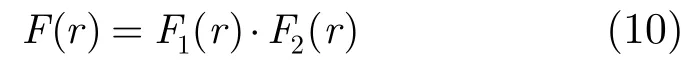
式中，F1(r)表示随机变量Ui(i=2,3,…,M)受到干扰的条件概率，而F2(r)表示随机变量Ui(i=b,b+1,…,M)未受到干扰的条件概率，且0≤b≤M。故F1(r)和F2(r)分别表示为

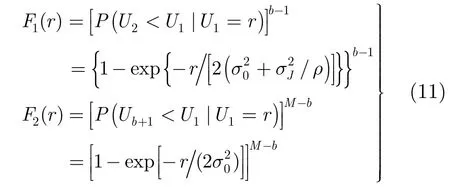
本文将从新PBNJ模型下跳频信号存在的4种状态来分析误符号率。

(1)当1Z=时，将bM=代入式(11)，联合式(9)和式(10)求解并化简后，得到误符号率11sP为

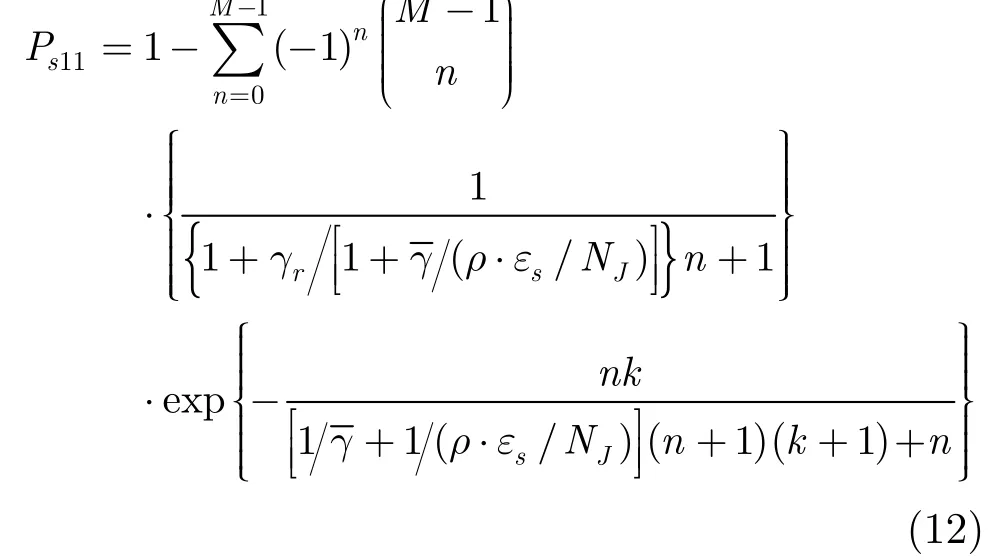
(2)当2Z=时，误符号率12sP为

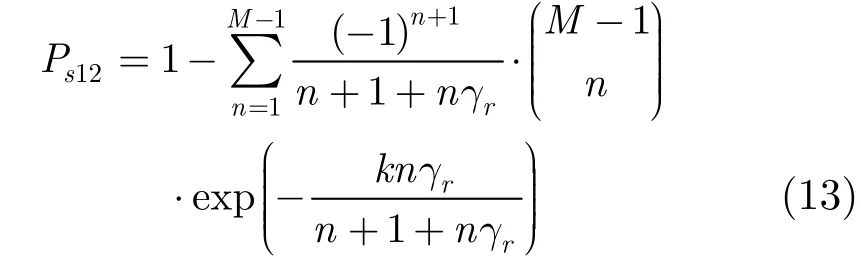
(3)当Z=3且跳频信号跳进WJ2所在跳频子带时，将b=l2代入式(11)，联合式(9)和式(10)求解并化简后，得到误符号率Ps21为

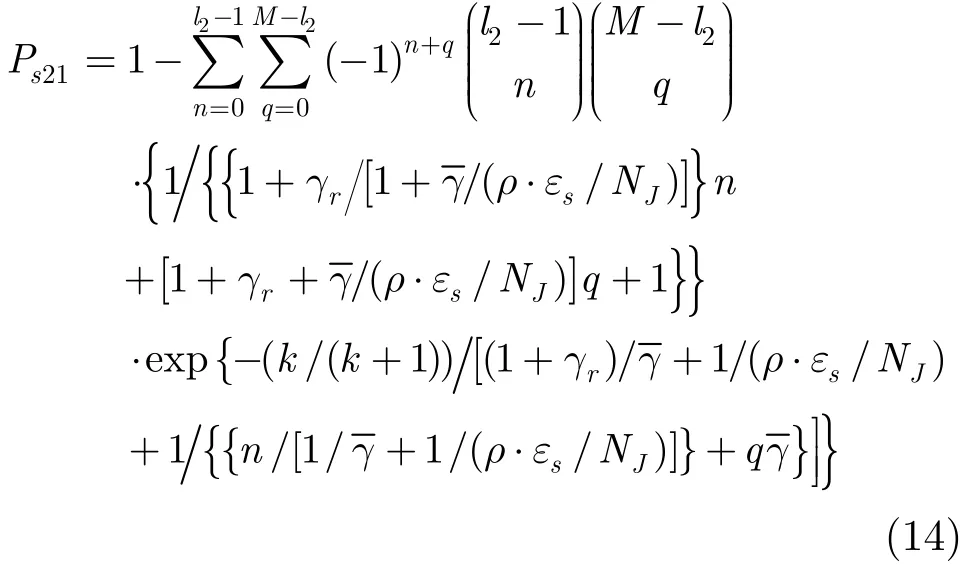
同理，跳频信号跳进3JW所在跳频子带时，误符号率31sP为

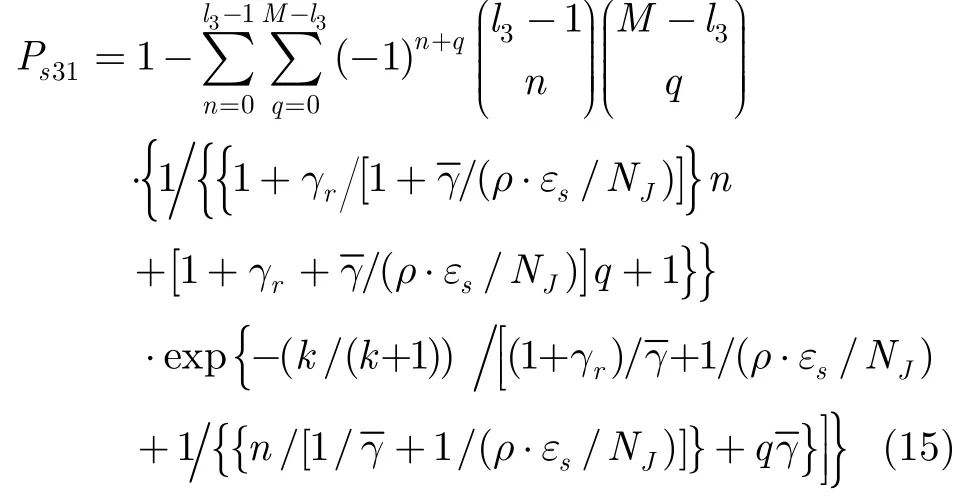
(4)当Z=4，跳频信号跳进WJ2所在跳频子带时，将b=l2代入式(11)，联合式(9)和式(10)求解并化简后，得到误符号率Ps22为

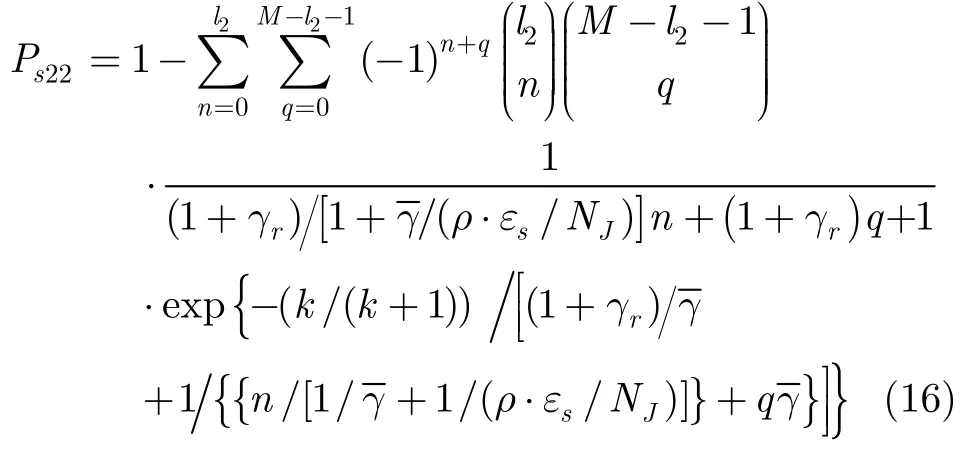
同理，跳频信号跳进3JW所在跳频子带时，误符号率32sP为

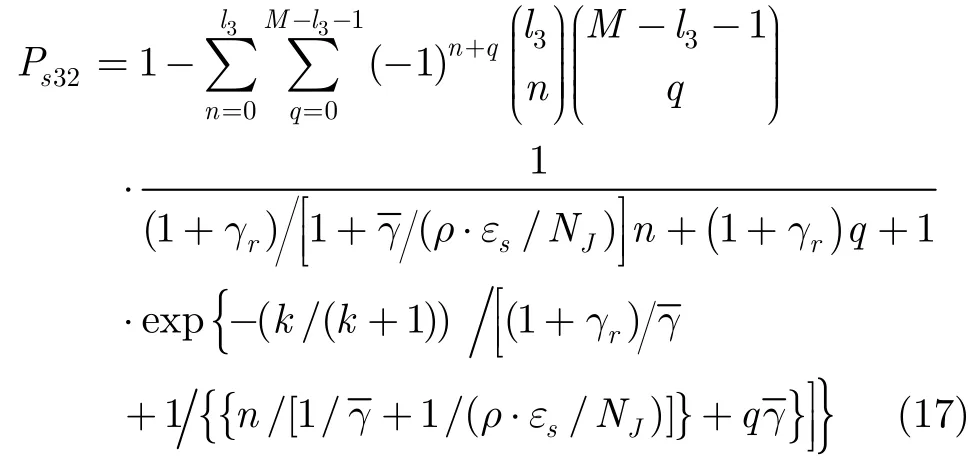
假定M个信号是先验等概，联合式(3)，式(12)～式(17)，可以得到FH/MFSK信号误符号率为

最后，由FH/MFSK信号的误符号率sP可得到FH/MFSK信号的误比特率bP。

4 理论与仿真结果

本节将从理论与仿真两个方面对比分析传统和新PBNJ模型对FH/MFSK信号的BER性能影响。设FH/MFSK信号的跳频速率为Rh=5000(跳/s)，εb/N0选取无干扰信道下使BER性能为1×10-5的值，具体的FH/MFSK系统参数如表1所示。首先利用Matlab的Simulink搭建仿真链路，对第3节得到的BER理论结果进行仿真验证，对比分析传统和新的PBNJ模型对FH/MFSK信号的BER性能影响。如图3所示，在莱斯因子k=0, k=4和k=∞下FH/MFSK信号的BER仿真性能分别与其理论值完全吻合，证明了BER理论分析的正确性。同时也可以从图3看出，传统与新PBNJ模型下的BER存在误差，例如，当BER为1×10-3, k=0(瑞利衰落信道)，k=4(莱斯衰落信道)和k=∞(高斯信道)时，新PBNJ模型比传统PBNJ模型下的BER性能增加约0.7 dB, 0.2 dB和0.5 dB。这说明了在3种典型信道的条件下，传统PBNJ模型由于干扰带宽最小分辨率不够精确，均会造成BER性能分析存在一定误差，瑞利衰落信道下误差最大。

然后，从理论上分析了MFSK调制阶数M对BER性能的影响。如图4所示，传统与新PBNJ模型下的BER存在误差，这说明了传统PBNJ的不足。从图4也可以看出，M越小，误差越明显，并且hN越小，此误差效果会更加明显。其次，从理论上分析了新PBNJ模型中干扰因子ρ对BER性能的影响。从图5可以看出，干扰带宽越窄，干扰带宽最小分辨率对系统的BER的影响越大。

最后，从理论上对比了传统与新PBNJ模型下最坏BER的性能的影响。如图6所示，当Nh=8时，传统与新PBNJ模型的最坏BER分别出现在ρ=3/8与ρ=9/32；当Nh=64时，传统与新PBNJ模型的最坏BER分别出现在ρ=25/64与ρ=97/ 256。因此，传统与新PBNJ模型下BER存在误差，这说明了传统PBNJ的不足。从图6也可以看出，Nh越小，误差越明显。

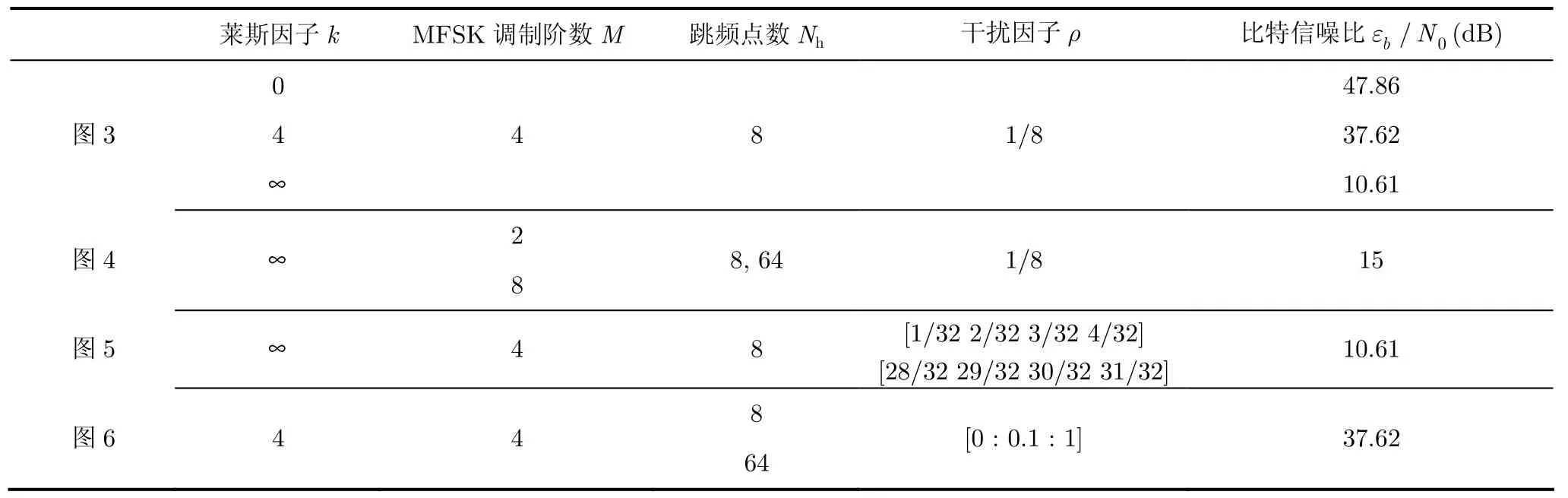
表1 系统参数

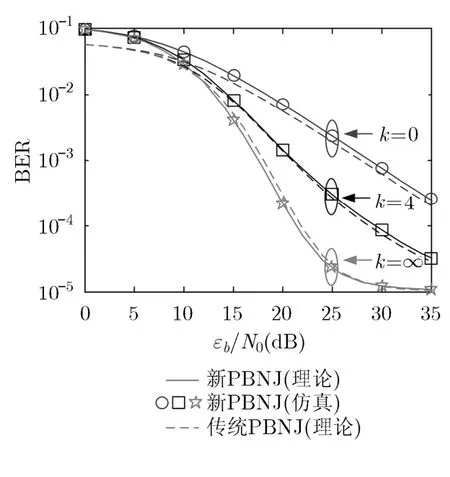
图3 不同赖斯因子k下的传统与新PBNJ下的BER性能对比

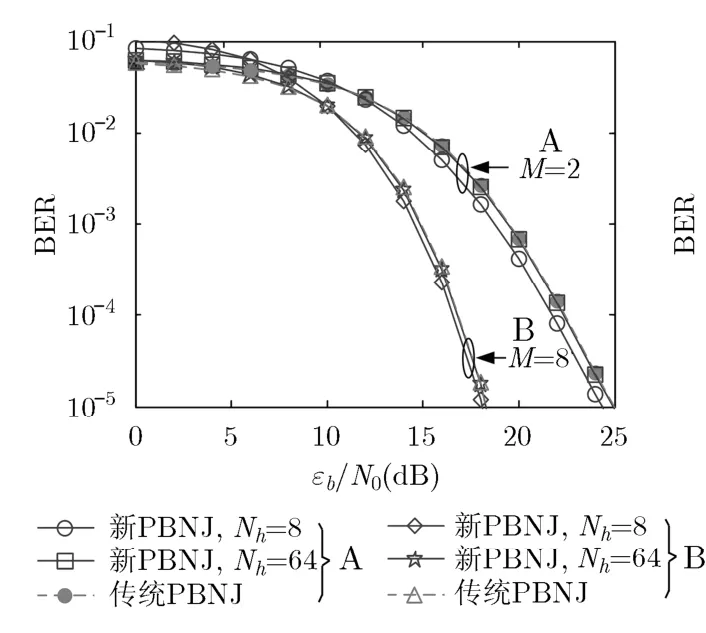
图4 调制阶数M对BER性能影响对比

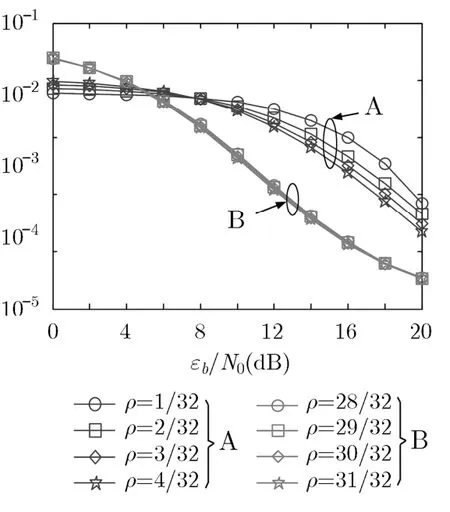
图5 在新PBNJ模型中干扰 因子ρ对BER性能对比

图6 最坏情况下的BER性能对比

5 结束语

本文针对FH/MFSK系统，研究了一种将干扰带宽最小分辨率精确到MFSK信号的带宽的1/M的新PBNJ模型。将无线信道建模为莱斯衰落信道，推导出了BER的闭合式，并通过计算机仿真验证了理论分析的正确性。理论分析与仿真结果表明传统与新PBNJ模型下FH/MFSK信号的BER性能存在差异，并且M,hN,ρ越小，差异越明显。因此，新的PBNJ模型更贴近真实的干扰环境。下一步工作将对新PBNJ模型的最坏PBNJ条件进行理论推导。

[5] Bird J and Felstead E. Antijam performance of fast frequency -hopped M-ary NCFSK——an overview[J]. IEEE Journal on Selected Areas in Communications, 1986, 4(2): 216-233.

[6] 于淼, 王曰海, 汪国富. 基于BSS的跳频通信抗部分频带噪声阻塞干扰方法[J]. 系统工程与电子技术, 2013, 35(5): 1079-1084.

Yu Miao, Wang Yue-hai, and Wang Guo-fu. Bss based antijamming method for frequency hopping communication against partial-band noise jamming[J]. Systems Engineering and Electronics, 2013, 35(5): 1079-1084.

[7] 夏志忠, 朱丽平, 卢晓威. FFH/BFSK AGC接收机在部分带干扰Nakagami衰落信道下的性能分析[J]. 电子与信息学报, 2007, 29(4): 963-966.

Xia Zhi-zhong, Zhu Li-ping, and Lu Xiao-wei. Performance of FFH/BFSK AGC receiver over a Nakagami-fading channel with partial-band jamming[J]. Journal of Electronics & Information Technology, 2007, 29(4): 963-966.

[8] Zhang J, The K C, and Li K H. Maximum-likelihood FFH/ MFSK receiver over Rayleigh-fading channels with composite effects of MTJ and PBNJ[J]. IEEE Transactions on Communications, 2011, 59(3): 675-679.

[1] Simon M K, Omura J K, Scholtz R A, et al.. Spread Spectrum Communication Handbook[M]. New York: McGraw-Hill, 2002: 3-37.

[2] 那丹彤, 赵维康. 跳频通信干扰与抗干扰技术[M]. 北京: 国防工业出版社, 2013: 203-215.

Na Dan-tong and Zhao Wei-kang. Technology of Frequency Hopping Communication Jamming and Anti-jamming[M]. Beijing: National Defense Industry Press, 2013: 203-215.

[3] Poisel R A. Modern Communications Jamming Principles and Techniques[M]. London: Artech House, 2005: 153-178.

[4] Esli C and Deliç H. Antijamming performance of spacefrequency coding in partial-band noise[J]. IEEE Transactions on Vehicular Technology, 2006, 55(2): 466-476.

[9] Le L M D and Teh K C. Maximum-likelihood FFH/MFSK receiver with MTJ and PBNJ over frequency-selective Rayleigh fading channels plus timing and frequency offsets [C]. 9th International Conference on Communications and Signal Processing (ICICS), Tainan, 2013: 1-5.

[10] Yao H, Huang J C, and Wornell G W. Achieving high bandwidth efficiency under partial-band noise jamming [C]. Military Communications Conference (MILCOM), San Diego, 2013: 1133-1138.

[11] 董彬虹, 程乙钊, 王达. 宽带MFSK/DFH系统抗部分频带噪声干扰性能分析 [J]. 信号处理, 2012, 28(3): 361-366.

Dong Bin-hong, Cheng Yi-zhao, and Wang Da. Performance analysis of wideband MFSK/DFH system with partial-band noise jamming[J]. Signal Processing, 2012, 28(3): 361-366.

[12] Song Yan-guang, Dong Bin-hong, and Tang Peng. Performance of DFH system in PBNJ over Rician fading channels[C]. 8th International ICST Conference on Communications and Networking in China (CHINACOM), Guilin, 2013: 124-128.

[13] 刘大龙. 宽间隔 MB-MFSK系统性能分析[D]. [硕士论文], 电子科技大学, 2013: 10-60.

Liu Da-long. Wide interval mapping MB-MFSK communication system[D]. [Master dissertation], University of Electronic Science and Technology of China, 2013: 10-60.

[14] Liang J J, Jeng L D, and Wang C H. A new partial-band noise jamming model for frequency-hopped MFSK systems[C]. 2nd International Symposium on Wireless Communication Systems, Siena, 2005: 200-204.

[15] Proakis J G and Salehi M. Digital Communications (Fifth Edition)[M]. New York: McGraw-Hill Higher Education, 2011: 216-219.

杜 洋： 男，1988年生，博士生，研究方向为抗干扰无线通信关键技术研究.

董彬虹： 女，1972年生，研究员，博士生导师，研究方向为无线通信关键技术研究.

唐 鹏： 男，1989年生，硕士生，研究方向为扩频通信技术研究.

周兰林： 男，1986年生，硕士生，研究方向为扩频通信技术研究.

Performance Analysis of FH/MFSK System in the Presence of New Partial-band Noise Jamming Model

Du Yang Dong Bin-hong Tang Peng Zhou Lan-lin
(National Key Laboratory of Science and Technology on Communications, University of Electronic Science and Technology of China, Chengdu 611731, China)

Partial-Band Noise Jamming (PBNJ) is one main type of narrow-band jamming, it has a huge impact on the performance of communication systems. The minimum resolution of jamming bandwidth of the conventional PBNJ model is the Frequency-Hopping (FH) sub-band bandwidth (Multiple Frequency Shift Keying (MFSK) signal bandwidth) in the FH/MFSK system. However, it is not always reasonable, thus a new PBNJ model, whose minimum resolution of jamming bandwidth can accurate to 1/M of the MFSK signal bandwidth is studied. In this paper, the closed-form expressions of Bit Error Rate (BER) performance under the new PBNJ model over Rician fading channel are derived and validated by computer simulations. The theoretical and simulation results show that the BER performance difference between the new and conventional PBNJ models is larger for smallerM,Nh,ρ.

Frequency Hopping (FH) communication; Partial-Band Noise Jamming (PBNJ); Minimum resolution of jamming bandwidth; Rician fading channel

TN914.4

A

1009-5896(2015)03-0721-06

10.11999/JEIT140708

2014-05-27收到，2014-09-15改回

国家自然科学基金(61201126)，新世纪优秀人才支持计划(NCET-11-0058)，国家部委基金和四川省青年科技基金(2012JQ0020)资助课题

*通信作者：杜洋 yangdu1988@gmail.com