基于空时自适应处理的低空风切变风速估计方法

吴仁彪张 彪 李 海 卢晓光 韩雁飞

(中国民航大学天津市智能信号与图像处理重点实验室 天津 300300)

基于空时自适应处理的低空风切变风速估计方法

吴仁彪*张 彪 李 海 卢晓光 韩雁飞

(中国民航大学天津市智能信号与图像处理重点实验室 天津 300300)

针对机载气象雷达在探测低空风切变时，有用信号会淹没在强杂波背景中的问题，该文提出一种基于空时自适应处理(STAP)的低空风切变风速估计方法。该方法首先利用空时插值原理校正机载前视阵地杂波的距离依赖性，获得多个独立同分布(IID)样本后估计地杂波协方差矩阵，然后构造适用于分布式低空风切变目标的空时自适应处理器，在自适应抑制地杂波的同时积累低空风切变信号，最终实现风场速度的精确估计。仿真结果表明，在高杂噪比、低信噪比的情况下，该方法可有效地自适应抑制地杂波并精确地估计风场速度。

机载气象雷达；低空风切变；风速估计；空时自适应处理

1 引言

机载气象雷达可对雷雨、风切变、湍流等灾害天气进行探测与预警，是飞机实时感知航路气象的重要设备，其对危险天气的探测能力对保证飞机行驶的安全性至关重要[1]。低空风切变常指高度600 m以下风向、风速突然变化的气象现象，通常是强气流由空中冲击到地面后向四周扩散的过程。低空风切变具有发生突然、时间短、尺度小、强度大和不易检测等特点，当飞机起飞和着陆进入强低空风切变区域时，会面临由风向、风速变化带来的升力损失，若处理不得当或缺乏足够的调节空间就可能遭遇飞行事故。因此，低空风切变检测技术的研究已是航空运输领域的一项重要课题[2]。

机载气象雷达下视检测低空风切变时，有用信号会被强地杂波所覆盖。在传统的低空风切变检测流程中，地杂波的抑制效果直接影响低空风切变的风速估计结果[2]。传统的在地杂波背景下估计风场风速的方法[3,4]包括杂波图法、基于参数化模型的谱估计方法、利用模式分析的扩展Prony方法、零陷滤波器法等，文献[5]提出一种基于压缩感知的低空风切变风速估计方法，能够在脉冲数较少时实现风速的精确估计，但该方法在应用时需要确定杂波谱宽，且并未涉及风速估计过程中的强杂波抑制问题。这些方法的本质在于寻找合适的凹口在抑制地杂波的同时保留风切变信号，但在强杂波背景下，地杂波难以完全消除，残余杂波仍会覆盖掉风切变信号的多普勒信息，影响风速估计结果的准确性。

相对于传统机载气象雷达的单天线体制，相控阵天线体制具有灵活度高、扫描速度快、易于波束赋形的优点，并且其回波信号中包含目标空间采样信息。目前国外已经对机载相控阵气象雷达开展了相关的研究工作。2013年9月，美国国家大气研究中心(National Center for Atmospheric Research, NCAR)表示，美国正在研制的下一代机载气象雷达[6,7]采用双极化相控阵体制。STAP[8]是机载相控阵雷达杂波抑制与目标检测的关键技术，可在对有用信号输出功率不变的条件下，尽可能地抑制杂波、干扰及噪声。STAP技术在目标检测与参数估计方面已有应用[9,10]，但此种应用多针对点目标，不能直接用于低空风切变等分布式目标的检测与估计，且机载气象雷达工作在前视状态，前视阵的杂波谱在距离上不平稳，因此传统的STAP方法不能直接应用于机载气象雷达中。

本文提出了一种基于STAP的低空风切变风速估计方法，该方法首先利用空时插值原理校正机载前视气象雷达杂波谱的距离依赖性，然后利用空时自适应处理器抑制地杂波并匹配低空风切变信号，估计风切变信号的多普勒频率并计算风场风速，最终实现机载前视气象雷达对分布式低空风切变目标的有效检测。仿真结果表明：在高杂噪比、低信噪比的情况下，该方法能够自适应地抑制地杂波并积累低空风切变信号，从而得到精确的风速估计结果。

2 信号模型

设机载平台上沿航向垂直方向均匀放置N元线阵，接收回波信号包括地杂波、低空风切变信号和噪声，假设杂波无起伏无模糊，噪声为加性高斯白噪声。

2.1 地杂波

如图1所示，地面散射单元水平方位角和俯仰角表示为θ和φ，则杂波单元空间角频率和时间角频率[8]可分别表示为ωs,1(θ,φ)和ωt,1(θ,φ)，且有

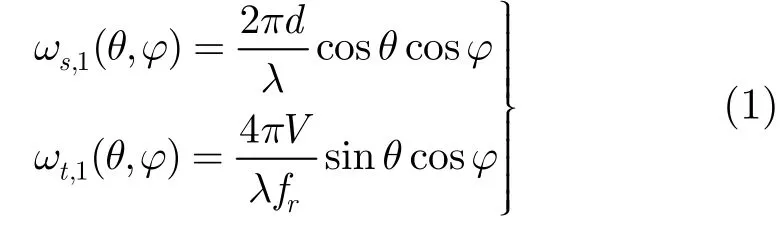
设cl(n,k)表示第n个阵元的第k个脉冲对第l个距离单元地面的接收数据，则有

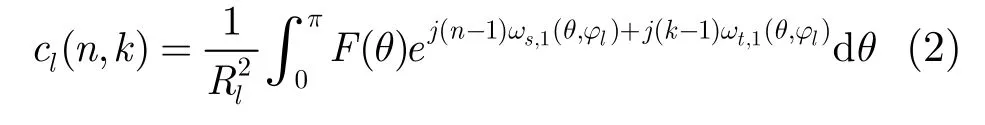
图1 机载前视阵示意图

其中，n=1,2,…,N, N为阵元数；k=1,2,…,K, K为一个相干处理时间内的脉冲数；l=1,2,…,L, L为距离单元数；V为载机速度；fr为脉冲重复频率；d为阵元间隔；F(θ)为天线方向图；Rl为第l个距离单元相对应的雷达斜距。

2.2 低空风切变信号

利用流体动力学仿真软件Fluent对低空风切变场建模[11]，得到低空风切变的密度场与速度场。由于低空风切变回波功率远远低于地杂波，本文只考虑风切变主瓣回波。将波束范围内每个散射点的回波相叠加，得到风切变场雷达回波，设sl(n,k)表示第n个阵元的第k个脉冲对第l个距离单元内低空风切变场的接收数据，则有

其中

式(3)和式(4)中，Q表示波束范围内的散射点数，ωs,2(θq,φq)和ωt,2(θq,φq)分别为第q个散射点的空间角频率和时间角频率；vq为该散射点与飞机的相对速度；Rq为该散射点与飞机的斜距。

2.3 回波信号

雷达回波信号x=s+c+n，其中s为低空风切变信号，c为地杂波，n为高斯白噪声，矩阵形式可写为

如图2所示为补偿飞机速度后的仿真信号空时2维谱(本图仿真条件中暂时设置风切变信号与地杂波功率相同，仅为便于观察杂波与信号的空时分布特性，实际情况下风切变信号要比地杂波功率小得多，本文后续研究中仿真条件按实际情况设定)，地杂波的空时2维谱呈现椭圆形分布，低空风切变信号的空时2维谱表现为主瓣波束空间锥角方向上的一条“窄带”。本文方法利用空时自适应处理器在地杂波方向形成凹口，在风切变信号方向形成增益，进而得到风场多普勒频率的有效估计结果。

图2 补偿飞机速度后的仿真信号空时2维谱

3 基于STAP的低空风切变风速估计方法

机载前视阵雷达的杂波分布具有距离依赖性[12,13]，直接使用回波信号估计杂波协方差矩阵，会致使STAP的杂波抑制性能严重下降。本文方法首先利用空时插值法校正机载前视阵杂波谱的距离依赖性，以获得求取杂波协方差矩阵所需要的独立同分布(Independent and Identically Distributed, IID)样本，然后利用STAP方法抑制地杂波并估计待检测距离单元内的风切变多普勒中心频率，处理工作范围内所有距离单元后得到风场速度随距离的变化曲线。

3.1 空时插值法

空时插值法[14,15]通过一个插值变换矩阵使得训练距离单元的杂波空时分布与待检测距离单元的空时分布一致，可有效校正杂波距离依赖性，进而精确估计待检测距离单元的杂波协方差矩阵。具体实现步骤为：

步骤1 选取第i号距离单元为待检测距离单元，构造待检测距离单元的空时导向矢量矩阵iV。首先将水平方位角均匀分成M份，得到对应。然后构造每个水平方位角θm和距离单元俯仰角φi对应的空时导向矢量v(θm)=vt(θm)vs(θm)。其中

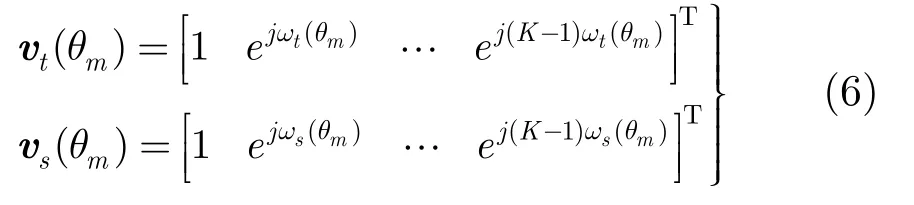
式(6)中j为虚数单位，可以得到待检测距离单元的空时导向矢量矩阵为

步骤2 选取第j号距离单元为参考距离单元，构造该参考距离单元的空时导向矢量矩阵jV，可得到第j号与第i号距离单元的插值变换矩阵为Tj,i=Vi(Vj)+，其中(⋅)+表示求伪逆运算。处理后的参考距离单元数据为yj=Tj,ixj，其与待检测距离单元内杂波的空时2维分布一致；

步骤3 更新参考距离单元，同样利用空时插值法进行处理，可以得到与待检测距离单元杂波分布特性相同的多个IID样本；

步骤4 根据先验信息补偿载机运动对回波信号相位的影响后，估计待检测单元杂波协方差矩阵为

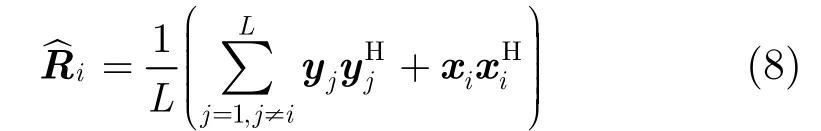
3.2 基于STAP的风速估计方法

可在抑制地杂波的同时匹配低空风切变信号的空时自适应处理器[16]可以描述为如式(9)所示的数学优化问题：

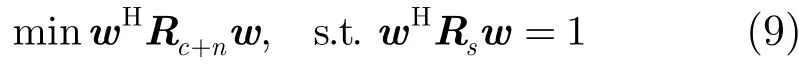
其中w为处理器权矢量，cn+R为杂波噪声协方差矩阵，sR为低空风切变信号协方差矩阵。为求解式(9)，构造代价函数

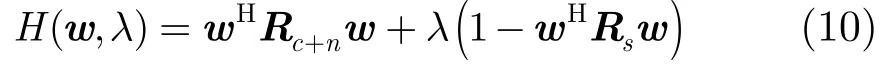
此时，拉格朗日算子λ可以看做是相应的广义特征值。由于矩阵Rc+n和Rs是半正定的[16]，所以式(11)得到的所有广义特征值都是非负实数。当式(11)成立时，代价函数取得最小值λ。将左乘到式(11)两边，得到

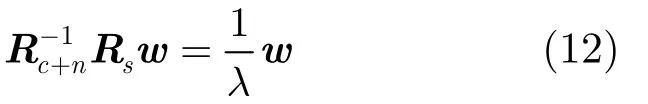
风切变目标Rs的参数化模型[2]为

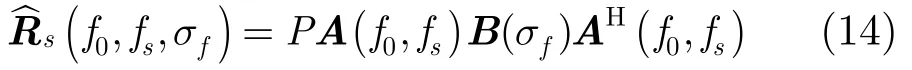
其中P为回波信号功率，fs=cosθ0cos φ0为信号空间频率，f0为信号多普勒中心频率，σf为信号多普勒谱宽，且有

式(15)中，Bt为K×K维矩阵，且Bt(a,b)=, Bs为N×N维全1矩阵。

风切变目标sR的参数化模型可由其回波模型推导得到。低空风切变属于分布式目标，其多普勒频率随距离的分布呈反“S”形，且单距离单元内的风切变信号在多普勒域内存在连续性展宽。基于此种特性，设定待检测距离单元内多普勒中心频率和多普勒谱宽，可以构造信号协方差矩阵ˆRs。某一距离单元内低空风切变回波模型可写为

其中zn,k为接收信号幅度，f为信号多普勒频率，且通常认为f～N(f0,)。此时，回波信号的相关函数为由信号相关函数即可推得风切变目标Rs的参数化模型如式(14)所示。

更新求解权矢量w时设定的多普勒中心频率f0，得到对不同多普勒频段目标信号进行匹配滤波的处理器权矢量，并分别求解处理器输出信号功率。当输出功率最大时，空时自适应处理器可以有效地抑制地杂波并积累低空风切变信号，此时设定的多普勒中心频率即为待检测距离单元内风切变信号的多普勒频率估计值，进而得到该距离单元的风速估计值为

谱宽σf表示了低空风切变场的风速变化率，可取为实际观测中风速谱宽的统计平均值[17]，本文选取σf=0.05。本文所提算法实质是在固定空间锥角ψ0和谱宽σf的情况下，利用STAP方法对待检测距离单元的多普勒中心频率做1维搜索。利用该算法依次对每个距离单元的回波数据进行风速估计，可得到风场速度随距离的变化情况。

3.3 算法流程

基于STAP的低空风切变风速估计方法的基本流程如图3所示。该方法是将相控阵体系引入到机载气象雷达中，利用空时插值法校正前视阵地杂波的距离依赖性，构造适用于低空风切变目标的空时自适应处理器，抑制地杂波并估计风切变信号的多普勒中心频率，最终实现风速的精确估计。在高杂噪比、低信噪比的情况下，本文方法仍能有效地抑制地杂波并精确地估计风场风速。针对待检测距离单元回波数据，核心处理步骤为：

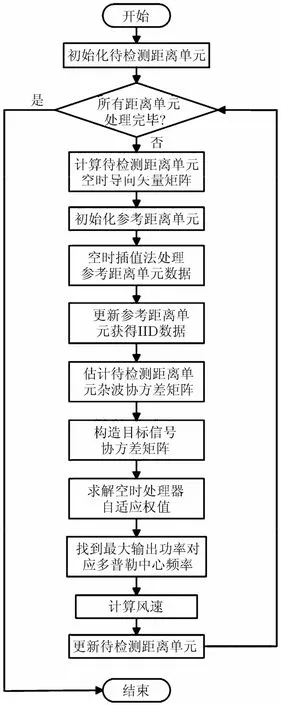
图3 基于STAP的低空风切变风速估计方法的基本流程图

步骤1 构造参考距离单元j与待检测距离单元i的插值变换矩阵Tj,i，处理参考距离单元数据xj，使其地杂波的空时2维分布与待检测距离单元趋于一致。依次处理所有距离单元数据，可得到与待检测距离单元杂波分布特性相同的多个IID样本；

步骤2 对接收信号进行相位补偿，剔除机载平台运动带来的多普勒偏移；

步骤3 空时插值处理与飞机速度补偿后，估计待检测距离单元杂波数据的统计协方差矩阵；

步骤4 利用风切变信号在多普勒域内存在连续展宽的性质，构造空时自适应处理器，抑制地杂波并匹配低空风切变信号，估计距离单元内的信号多普勒中心频率，计算得到风速估计结果。

4 仿真结果及分析

4.1 仿真条件描述

低空风切变场分布于飞机前方8.5～16.5 km处，天线阵为阵元数为N=8的均匀线阵，阵元间距d=λ/2，主瓣波束水平方位角为60°，俯仰角为0°，机载气象雷达工作波长为0.05 m，脉冲重复频率为7 kHz，最小可分辨距离150 m，相干处理脉冲数K=64，信噪比5 dB，杂噪比40 dB，飞机速度为75 m/s，飞行高度为600 m，多普勒谱宽σf=0.05。

4.2 仿真结果分析

图4(a)给出了利用空时插值法校正地杂波距离依赖性前的杂波功率谱，由于机载前视阵雷达的杂波分布具有距离依赖性，其空时2维谱有明显发散现象。机载前视阵的杂波样本不满足IID条件，直接使用接收数据估计杂波协方差矩阵，会致使STAP的杂波抑制性能严重下降。图4(b)给出了利用空时插值法向第20号距离单元做杂波谱补偿的结果，可以看出，补偿后的杂波空时2维谱明显变窄。

图5以20号距离单元为例，显示了f0=0.5, σf=0.05时的空时自适应处理器频响特性。可以看出，处理器沿杂波分布方向形成自适应凹口，同时对中心频率为f0的宽带信号进行功率积累。按f0循环，更新处理器的权矢量，得到最大输出功率对应的，即可计算此距离单元的风场风速。

利用本文方法在自适应抑制地杂波的同时，可实现目标信号多普勒频率的准确估计，全距离单元的频率估计结果如图6所示。在8.5～16.5 km范围内，信号的多普勒频率随距离呈现反“S”形分布，进一步估计风场危险程度后可完成低空风切变的检测过程。

本文方法与传统方法的风速估计结果对比如图7所示。在同等杂噪比与信噪比条件下，本文方法处理效果明显优于自适应频域置零法与固定凹口法等传统方法。结果证明，本文提出的基于STAP的低空风切变风速估计方法可以在强杂波条件下，有效地抑制地杂波，并精确估计风场速度。

图4 空时插值法补偿地杂波距离依赖性效果图

图5 空时自适应处理器频响特性

图6 全距离单元多普勒频率估计结果

图7 风场速度估计结果

5 结束语

针对低空风切变信号会淹没在强杂波背景中的问题，本文提出一种基于STAP的低空风切变检测方法。该方法是将相控阵天线体系引入机载气象雷达中，利用空时插值法校正前视阵地杂波的距离依赖性，估计地杂波协方差矩阵，代入求解处理器权矢量，自适应地抑制地杂波并估计得到风切变信号的多普勒中心频率，最终实现风速的精确估计。仿真结果表明，在强杂波背景下，本方法可以自适应地抑制地杂波并精确估计风场速度。

[1] Barber S, Paramore S, and Woodell D L. Airborne weather radar system and radar display[P]. US patent, 7109913B1, 2006-09-19.

[2] 韩雁飞. 强杂波背景下的低空风切变检测技术研究[D]. [硕士论文], 中国民航大学, 2013.

[3] Moscardini C, Berizzi F, Martorella M, et al.. Signal spectral modeling for airborne radar in the presence of windshear phenomena[J]. IET Radar, Sonar and Navigation, 2011, 5(7): 796-805.

[4] 白建, 李勇, 高霞, 等. 基于 Prony 模型的低空风切变快速检测算法[J]. 计算机测量与控制, 2009, 17(10): 1889-1891.

Bai Jian, Li Yong, Gao Xia, et al.. Low-level wind shear detection algorithm based on prony model[J]. Computer Measurement & Control, 2009, 17(10): 1889-1891.

[5] 吴仁彪, 韩雁飞, 李海. 基于压缩感知的低空风切变风速估计方法[J]. 电子与信息学报, 2013, 35(10): 2512-2517.

Wu Ren-biao, Han Yan-fei, and Li Hai. Wind speed estimation for low-attitude wind shear via compressive sensing[J]. Journal of Electronics & Information Technology, 2013, 35(10): 2512-2517.

[6] Loew E, Salazar J, Tsai P, et al.. Architecture overview and system performance of the airborne phased array radar (APAR) for atmospheric research[R]. Report of National Center for Atmospheric Research, Colorado: NCAR, 2013.

[7] Salazar L. Loew E, Tsai P, et al.. Design and development of a 2-D electronically scanned dual-polarization line-replaceable unit (LRU) for airborne phased array radar for atmospheric research[C]. Proceedings of 36th AMS Radar Conference, Breckenridge, US, 2013: 16-20.

[8] 王永良, 彭应宁. 空时自适应处理[M]. 北京: 清华大学出版社, 2000: 26-45.

Wang Yong-liang and Peng Ying-ning. Space-time Adaptive Processing[M]. Beijing: Tsinghua University Press, 2000: 26-45.

[9] Wu Ren-biao and Bao Zheng. Array pattern distortion and remedies in space-time adaptive processing for airborne radar[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(7): 963-970.

[10] Wang Yong-liang, Bao Zheng, and Peng Ying-ning. STAP with medium PRF mode for non-side-looking airborne radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 609-620.

[11] 吴仁彪, 孟志超, 范懿, 等. 机载气象雷达风切变信号仿真[J].现代雷达, 2012, 34(4): 74-78.

Wu Ren-biao, Meng Zhi-chao, Fan Yi, et al.. Wind shear signal simulation of the airborne weather radar[J]. Modern Radar, 2012, 34(4): 74-78.

[12] Kreyenkamp O and Klemm R. Doppler compensation in forward-looking STAP radar[J]. IET Radar, Sonar and Navigation, 2001, 148(5): 253-258.

[13] Yang Xiao-peng, Liu Yong-xu, and Long Teng. Geometry-aided subspace procection for mitigating range-dependence of the clutter spectrum in forward-looking airborne radar[C]. Proceedings of 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 2012: 6138-6141.

[14] Varadarajan V and Krolik J L. Joint space-time interpolation for distorted linear and bistatic array geometries[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 848-860.

[15] 刘锦辉, 廖桂生, 李明. 机载前视阵雷达杂波谱空时分离插值方法[J]. 电子与信息学报, 2011, 33(9): 2120-2124.

Liu Jin-hui, Liao Gui-sheng, and Li Ming. Space-time separated interpretation method for forward-looking airborne radar clutter spectrum[J]. Journal of Electronics & Information Technology, 2011, 33(9): 2120-2124.

[16] Shahbazpanahi S, Gershman A B, Luo Z Q, et al.. Robust adaptive beamforming for general-rank signal models[J]. IEEE Transactions on Signal Processing, 2003, 51(9): 2257-2269.

[17] 肖业伦, 金长江. 大气扰动中的飞行原理[M]. 北京: 国防工业出版社, 1993: 21-31.

Xiao Ye-lun and Jin Chang-jiang. Principles of Flight in Atmospheric Disturbances[M]. Beijing: National Defence Industry Press, 1993: 21-31.

吴仁彪： 男，1966年生，博士，教授，博士生导师，研究方向为自适应信号处理、阵列信号处理、信号谱分析及其在雷达、卫星导航和空中交通管理方向的应用等.

张 彪： 男，1991年生，硕士生，研究方向为机载气象雷达信号处理.

李 海： 男，1976年生，博士，副教授，硕士生导师，研究方向为干涉合成孔径雷达信号处理、空时自适应信号处理等.

Wind Speed Estimation for Low-attitude Windshear Based on Space-time Adaptive Processing

Wu Ren-biao Zhang Biao Li Hai Lu Xiao-guang Han Yan-fei

(Tianjin Key Lab for Advanced Signal Processing, Civil Aviation University of China, Tianjin 300300, China)

When detecting low-attitude windshear with airborne weather radar, the real signals are usually covered with strong clutter. In this paper, a novel method of low-attitude windshear speed estimation based on Space-Time Adaptive Processing (STAP) is proposed to solve the above problem. The proposed method handles the range-dependence of clutter of airborne forward looking array with space-time interpretation theory to achieve the Independent and Identically Distributed (IID) samples used in the clutter covariance matrix estimation; then the space-time adaptive processor is constructed which is applicable to a distributed low-attitude windshear target to suppress clutter and accumulate windshear signal; finally the accurate estimation of wind speed is got. The experimental results show that the proposed method can achieve a superior clutter suppression performance and an accurate wind speed estimation in high clutter-to-noise ratio and low signal-to-noise ratio.

Airborne weather radar; Low-attitude windshear; Wind speed estimation; Space-Time Adaptive Processing (STAP)

TN959.4

A

1009-5896(2015)03-0631-06

10.11999/JEIT140697

2014-05-27收到，2014-08-07改回

国家自然科学基金(61231017, 61233109)和中央高校基本科研业务费项目(3122014D007)资助课题

*通信作者：吴仁彪 rbwu@cauc.edu.cn