地波雷达与自动识别系统目标点迹最优关联算法

张 晖刘永信*张 杰纪永刚郑志强

①(内蒙古大学电子信息工程学院 呼和浩特 010021)

②(国家海洋局第一海洋研究所 青岛 266061)

地波雷达与自动识别系统目标点迹最优关联算法

张 晖①刘永信*①张 杰②纪永刚②郑志强①

①(内蒙古大学电子信息工程学院 呼和浩特 010021)

②(国家海洋局第一海洋研究所 青岛 266061)

为了提高海洋探测精度和范围，针对高频地波雷达(HFSWR)和自动识别系统(AIS)目标点迹的融合利用问题，该文提出一种基于JVC(Jonker-Volgenant-Castanon)的点迹分状态全局最优关联算法。首先，通过判断高频地波雷达和AIS点迹的径向速度，将点迹分为准静态目标和动态目标。接着，选取径向速度和点迹间的球面距离为特征参数，对不同状态下目标点迹分别进行径向速度和位置间球面距离粗关联。最后，使用相对距离比的平均值进行关联效果的评价，通过选择合适的关联门限参数，使用JVC算法实现高频地波雷达和AIS的点迹最优关联。实验结果表明：该算法在关联相同点迹对数的情况下，关联精度高于最近邻(NN)算法和Munkres关联法，关联用时少于最近邻算法和Munkres关联法。通过近3年内3组不同时刻实测目标点迹的验证，该算法可以满足关联的实用性和实时性要求。

高频地波雷达；自动识别系统；数据关联；最优关联；JVC(Jonker-Volgenant-Castanon)算法

1 引言

海洋是国民经济可持续发展的战略空间，也是国家安全的重要屏障。卫星、航空、舰载及岸基雷达、舰船自动识别系统(Automatic IdentificationSystem, AIS)是目前海上船只目标的主要探测手段。AIS能提供合作舰船的经度、纬度、速度、对地航向、船号、船的长度和宽度等信息，且定位精度较高。高频地波雷达(High Frequency Surface Wave Radar, HFSWR)可实时监视监测并跟踪船只，但空间分辨率较低，定位精度低于AIS。利用高频地波雷达与AIS点迹数据融合信息，可以有效提高海上船只目标的探测范围和精度。对于某一时刻的目标点迹融合，必须准确地判断雷达和AIS点迹的对应关系，有效地判断哪些目标点迹信息是来自同一个目标的信息。

现有的雷达和AIS的融合应用主要分为两种：点迹融合[1,2]和航迹融合[3,4]。点迹融合主要关注某一时间点的目标分布情况，航迹融合则关注某一时间段的目标航迹情况。本文主要针对雷达和AIS点迹融合展开研究。国内外雷达和AIS的目标点迹融合主要集中在最近邻(Nearest Neighbor, NN)算法[5]、统计分析法[6,7]、反向传播(Back Propagation, BP)神经网络关联法[8]和模糊关联法[9]等算法。文献[5]将高频地波雷达数据与AIS和合成孔径雷达(Synthetic Aperture Radar, SAR)点迹数据使用最近邻算法进行关联，评估高频地波雷达的船只探测跟踪精度。文献[6]和文献[10]在分析雷达和AIS融合理论的基础上，提出协方差矩阵计算方法，同时针对融合中数据不一致问题，做了详细的分析。文献[7]通过对高频雷达探测中大量不同类型船只径向距离和径向速度等统计数据的分析，以AIS统计数据作为参考，从统计数据整体上评估雷达测试精度。文献[8]］对AIS和雷达点迹间利用BP神经网络进行关联做了研究准备工作。文献[9]使用一种基于最大隶属度关系的改进模糊互相关算法融合大量的雷达和AIS观测数据。文献[11]通过高频地波雷达和AIS信息的融合比对提出一种雷达天线校正算法。文献[2]和文献[12]通过径向速度、径向距离和方位角进行地波雷达与AIS点迹间的关联，取得了很好的关联效果。上述工作为地波雷达和AIS点迹关联提供了方法借鉴和参考。

JVC(Jonker-Volgenant-Castanon)分配是由Jonker, Volgenant和Castanon 3人共同提出的一种线性分配算法，常用于解决数据关联中的最优关联计算问题。针对实际应用环境中高频地波雷达和AIS目标点迹密集分布下的关联问题，本文借鉴多传感器的全局最优关联算法[13]，将JVC算法引入目标点迹关联中，以点迹间的球面距离作为代价函数，以相对平均距离比作为评价指标，进行最优球面距离的关联优化，实现高频地波雷达和AIS点迹的全局最优关联，从而为密集环境中的雷达和AIS目标点迹关联提供了一种新的实用算法。

2 数据源及数据预处理

实验时间为2011年10月31日，实验区在中国某海域，经纬度范围35.0º～40.0ºN, 117.5º～123.0ºE。实验数据包括覆盖实验区的高频地波雷达和AIS目标点迹数据。

高频地波雷达提供的目标点迹信息有探测频率、经度、纬度、径向速度、角度(与雷达主波束之间夹角)、探测距离。AIS信息包括经度、纬度、速度、对地航向、船号、船的长度和宽度等信息。鉴于不同运动状态的船只的AIS信息更新频率不同，选择高频地波雷达探测时间的前后5 min的AIS数据，从中选取雷达探测时间最近更新的AIS目标点迹信息作为该时刻的AIS目标点迹。

2011年10月31日:: 091850时刻高频地波雷达目标点迹如图1所示，AIS目标点迹如图2所示。该时刻，高频地波雷达共探测到336个目标点迹，AIS共探测到836个。从图1和图2中可以看出，AIS监测的范围大于高频地波雷达，图2中经纬度在35.0º～37.0ºN和117.5º～119.0ºE范围内的目标属于高频地波雷达所探测不到的区域，为了减少后续数据处理的复杂度，提前对AIS数据进行粗处理，对于监测范围属于35.0º～37.0ºN, 117.5º～119.0ºE的AIS目标不进行关联分析。

3 基于JVC的分状态数据关联算法

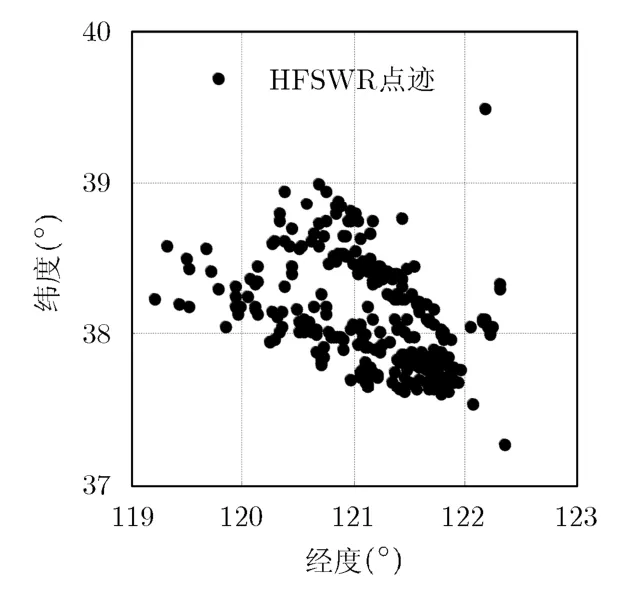
图1 2011年10月31日高频地波雷达目标点迹分布

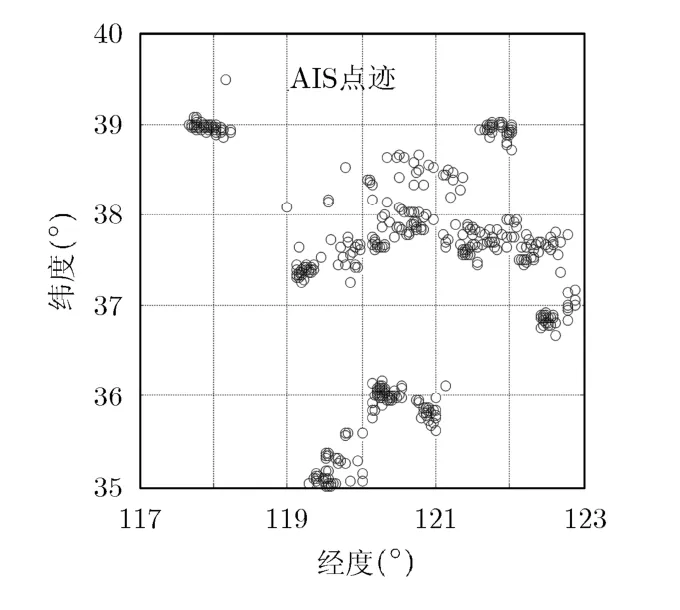
图2 2011年10月31日AIS目标点迹分布

常用的数据关联算法有最近邻算法、全局最近邻算法、联合概率数据关联(Joint Probability DataAssociation, JPDA)算法、多假设跟踪算法(Multiple Hypothesis Tracking, MHT)等[13]。高频地波雷达和AIS点迹数据探测范围不同，属于不同类别传感器之间的数据关联，点迹信息并不存在一一对应关系，干扰点不能通过杂波模型进行分析，JPDA和MHT算法无法应用。最近邻算法适用于点迹稀疏的情况下进行点迹关联，在点迹密集地区容易发生误关联。全局最近邻算法从全局考虑，寻找全局代价最小的最优关联，常见的最优关联算法中Munkres和JVC算法的最优分配效果优于拍卖算法，JVC算法的容错性优于Munkres算法和拍卖算法[14]。JVC算法在获得一一关联最优解的同时保持算法的高计算效率[13]，通过对数据的深入分析，采用分状态JVC最优关联算法进行高频地波雷达与AIS目标点迹关联。

3.1 特征向量的选择及计算

高频地波雷达的空间分辨率较低，如果高频地波雷达和AIS点迹仅以位置数据关联，在局部点迹密集区域，很容易造成误关联。为了提高关联的准确性，减少误关联，采用径向速度和距离作为关联的特征参数。

3.1.1 径向速度的计算 高频地波雷达点迹数据中提供径向速度，AIS点迹数据中未提供径向速度，采用式(1)计算AIS速度在径向角度的速度投影。

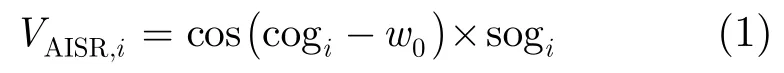
其中cogi为AIS点迹的对地航向，sogi为AIS点迹的航速，0w为雷达主波束角度。

3.1.2 点迹间球面距离的计算 高频地波雷达和AIS采用两点间的球面距离来进行关联，高频地波雷达与AIS两点间的球面距离Dist采用式(2)进行计算。

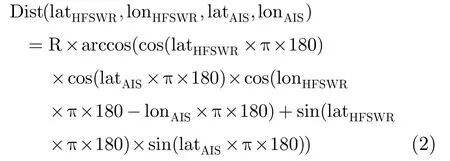
其中R为地球近似半径，lon, lat为高频地波雷达与AIS点迹的经度和纬度。

3.2 点迹分状态数据关联算法流程

在数据关联过程中，关联门限的选择至关重要，选择合适的关联门限，有助于对来自同一目标的不同传感器的点迹进行关联。船只在静止状态和运动状态下，由于运动速度的不同，雷达距离测量误差也会有所差别，因此本算法首先将准静止状态和运动状态的船只进行分类，采用不同的距离关联门限进行预关联，再分别使用JVC算法进行分状态最优距离关联。分状态数据关联算法流程如图3所示。

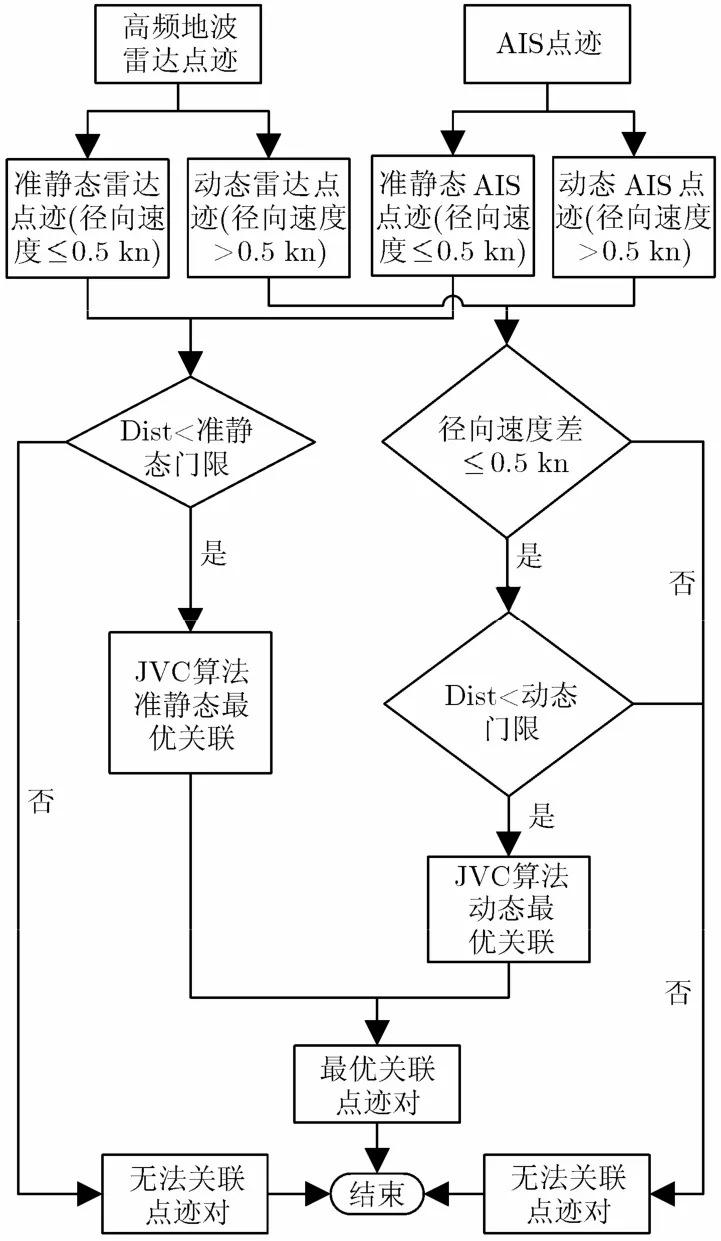
图3 分状态数据关联算法流程图

算法选取速度是否0.5≤kn来区分准静态和运动点迹，AIS准静态点迹所占的比例较高。准静态下，关联门限以式(3)实现，关联门限与高频地波雷达点的径向距离成比例，比例系数为K1。点迹距离雷达的径向距离越远，探测误差越大，关联门限越大。

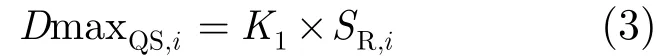
其中DmaxQS,i为准静态下第i个雷达点的关联门限值，SR,i为第i个雷达点的径向距离。

运动状态下，以高频地波雷达动态点迹遍历AIS点迹，首先进行速度关联，对于径向速度差小于0.5 kn的点迹进一步判断距离门限是否符合关联要求[8]，运动状态下的关联门限以式(4)实现，动态情况下的关联门限与径向距离和径向速度有关，距离和径向速度越大，测量误差越大，关联门限值越大。

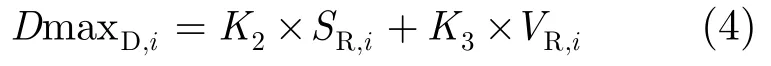
其中DmaxD,i为动态下第i个雷达点的关联门限值，VR,i为第i个雷达点的径向速度，K2为距离比例参数，K3为径向速度比例参数。

3.3 基于JVC最优距离匹配算法实现

JVC算法的模型是指在c[i,j]-u[i]-v[j ]≥0(i=1,2,…,m;j=1,2,…,n)的条件下求

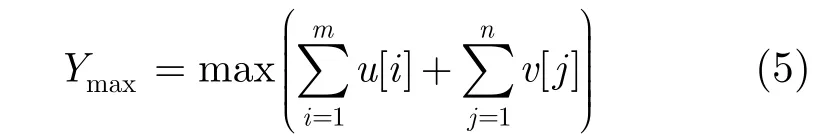
其中c[i,j]为代价函数，算法选择高频地波雷达和AIS两点间的球面距离作为代价函数，u[i]和v[j]分别代表行变量和列变量的分配代价，分别代表在最优解的过程中变量改变所导致的目标值的变化量[15]。最优解的求解过程就是寻找最佳的一对一点迹关联，使得关联点迹间的总球面距离最短。

在文献[16]的基础上，将JVC算法应用于高频地波雷达和AIS的点迹关联中，JVC算法最优距离匹配主要步骤为：

步骤1 将所有高频地波雷达点迹信息输入到先进先出的队列，选择队首的点迹信息开始处理。

步骤2 寻找与该高频地波雷达点迹距离最小的两个AIS点迹。

步骤3 计算两个AIS点迹的分配代价，初始分配代价为0，计算当前两条最佳匹配点迹的差值。

步骤4 分配高频地波雷达点迹到距离最小的AIS点迹，如果匹配成功，为已匹配AIS点迹的高频地波雷达点迹重新计算新的分配代价；如果该点迹已与其他点迹匹配，则重新计算分配代价，为冲突的点迹重新寻找最优匹配。

步骤5 继续下一点迹的匹配，直到所有雷达点迹匹配完毕或小于迭代阈值时，算法结束。

4 参数选择及算法验证

4.1 参数选择

关联算法的门限需要设置合适的参数K1, K2, K3，以达到匹配数与配对距离的平衡，采用试探法来选择各关联门限参数。考虑到随着雷达点迹径向距离的不同，雷达的测距误差会有明显的差别[2]。对于关联效果的评价，选择点迹间的相对距离比值的平均值作为主要评价因子。相对距离比计算如式(6)所示：

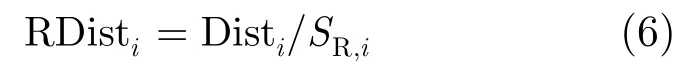
其中Disti为第i个关联雷达点迹与关联AIS点迹间的球面距离。经过测算在径向距离为200 km时，两点间的距离可以达到19 km[2]，选择0.095作为相对距离比的平均值的参考上限。

4.1.1 准静态门限参数K1的选择 如表1所示，随着K1值的逐步增大，准静态下相对距离比的平均值和关联点数也逐步增加，当K1=0.29时，相对距离比的平均值迅速增大到0.1104，考虑到准静态下的误差距离值较小，选择K1=0.28。

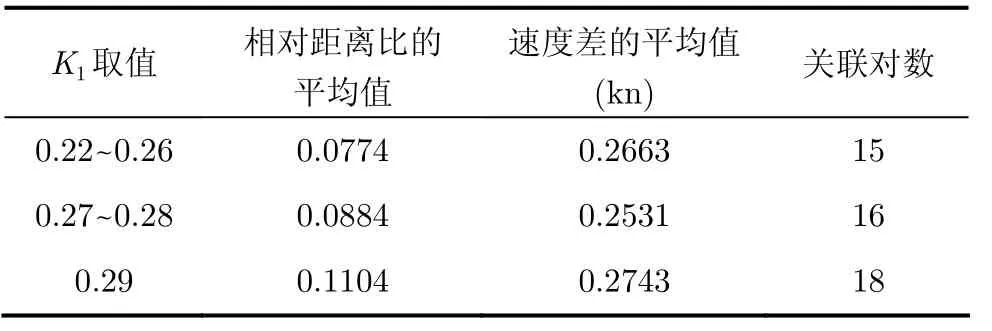
表1 K1的取值对准静态关联的影响

4.1.2 动态门限参数K2的选择 考虑到径向距离对距离的测算影响较大，所以选择K2作为影响动态关联的主要因素。选择K3=0时，随着K2的增加，动态关联情况变化如表2所示，当K2=0.20时，相对距离比的平均值变化较大，增大到0.0974，超出0.095，所以选择K2=0.19，由K3进行微调。

4.1.3 动态门限参数K3的选择 确定参数K2后，对K3的参数进行调整，K3变化对关联情况的影响如表3所示。当K3=0.15，相对距离比的平均值增大到0.1012，但是关联对数无明显变化，因此选择K3=0.11。

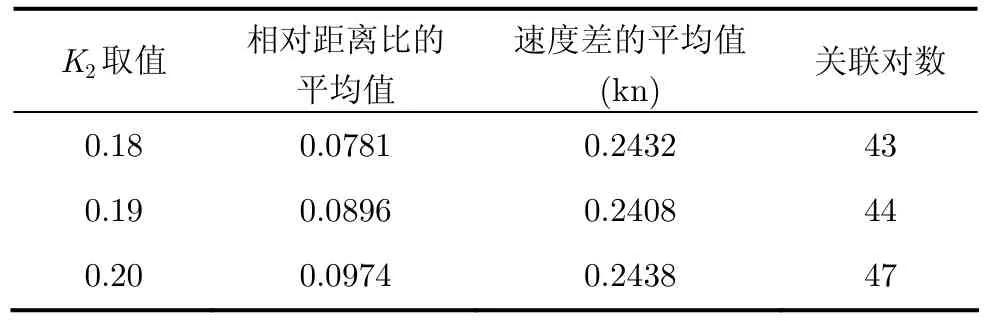
表2 K2的取值对动态关联的影响

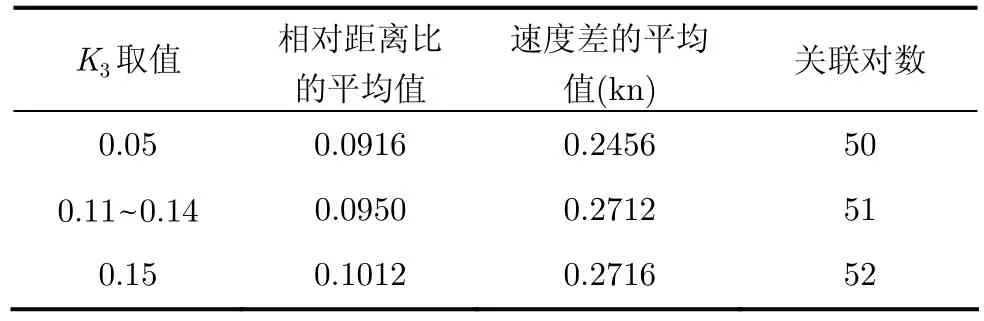
表3 K3的取值对动态关联的影响

4.2 算法验证及比较

分别采用最近邻算法、Munkres算法、分状态JVC关联算法对2011年10月31日:: 091850时的336个雷达目标点迹和443个AIS点迹进行点迹关联比较。

最近邻算法在阈值选取较小的时候关联效果较好。但当阈值增大时，最近邻算法关联效果会明显变差，关联51对时，关联如图4所示，图中实线连接表示实线两端的雷达点迹和AIS点迹为关联点迹对。

Munkres关联算法采用式(4)计算关联门限，关联效果如图5所示，关联51对时，相对距离比的平均值为0.1159。

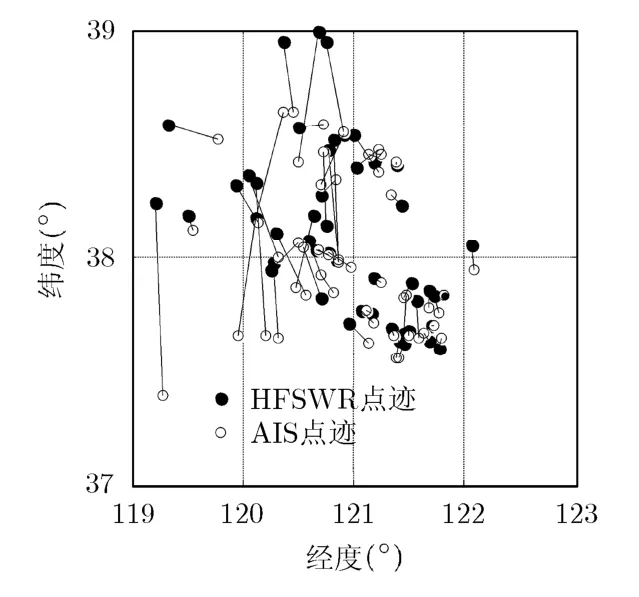
图4 最近邻算法关联效果

图5 Munkres算法关联效果

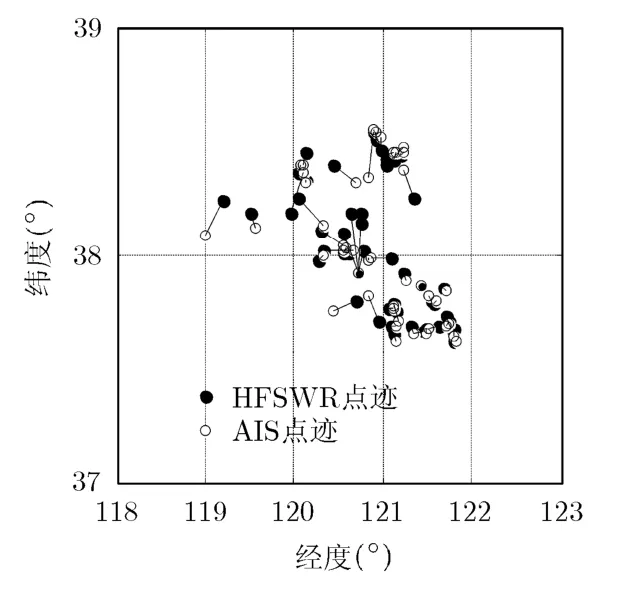
图6 分状态JVC关联效果

分状态JVC关联算法关联效果如图6所示，在关联51对的情况下，相对距离比的平均值为0.0950。

在同样关联51对点迹的情况下，各算法关联结果比较如表4所示。最近邻算法关联的相对距离比的平均值最大，Munkres算法次之，分状态JVC关联算法最小，同时分状态关联算法计算时间也明显优于最近邻和Munkres算法。

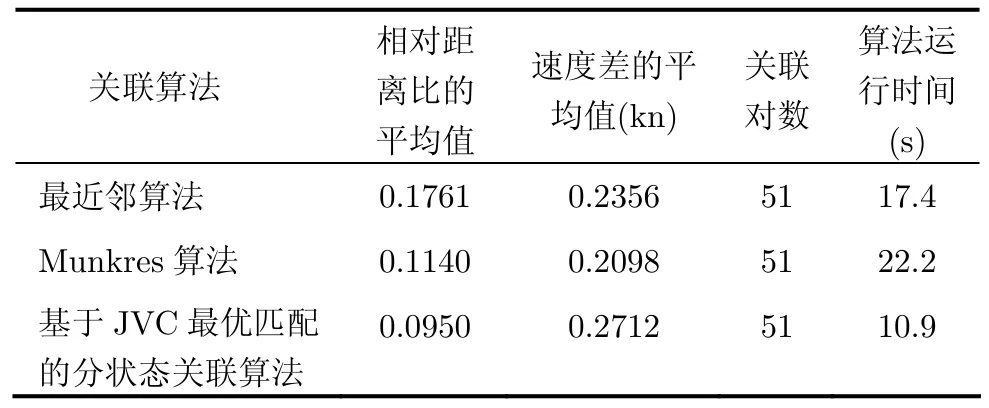
表4 3种数据关联算法的比较

4.3 算法实用性和实时性

为了验证算法的实用性，分别采用2012年4月23日10:10:45时和2013年9月6日09:18:45时的两组实验数据，进行分状态JVC数据关联验证，其中2012年4月23日的数据共包含273个雷达点迹和474个AIS点迹；2013年9月6日共包含262个雷达点迹和874个AIS点迹。

算法的实验结果如表5所示，选择相对距离比的平均值的比值不大于0.095的最大关联情况作为关联条件，分状态JVC数据关联算法可以保持约15%的关联比例，对于273个雷达点迹和474个AIS点迹的数据关联，在硬件环境为Intel Core i3 CPU @3.3 GHz处理器和4 G内存的普通计算机上可以在10 s内完成，满足数据关联的实时性要求。

5 结束语

本文针对高频地波雷达与AIS点迹信息融合应用问题，将线性分配JVC算法应用于雷达与AIS点迹的最优匹配中，实现了点迹间距离的最优化匹配，解决了点迹密集分布环境下的数据关联。在关联过程中，为了提高运算速度和匹配精度，通过径向速度的判断将点迹信息划分为准静态和动态点迹，对于不同状态的点迹分别进行JVC最优匹配，有效实现了分状态下目标点迹的最优关联。实验结果表明，该算法在同样关联51对点迹的情况下，关联精度高于最近邻算法和Munkres法，关联用时少于最近邻法和Munkres法，为地波雷达与AIS目标点迹关联提供了一种可行的方法。但是，由于雷达的目标定位精度较低，雷达与AIS的点迹关联比例较低，下一步可以考虑进一步融合高精度的SAR图像数据进行船只点迹目标融合探测，以便提高海洋探测的精度和范围，同时可以起到校准雷达精度的作用。

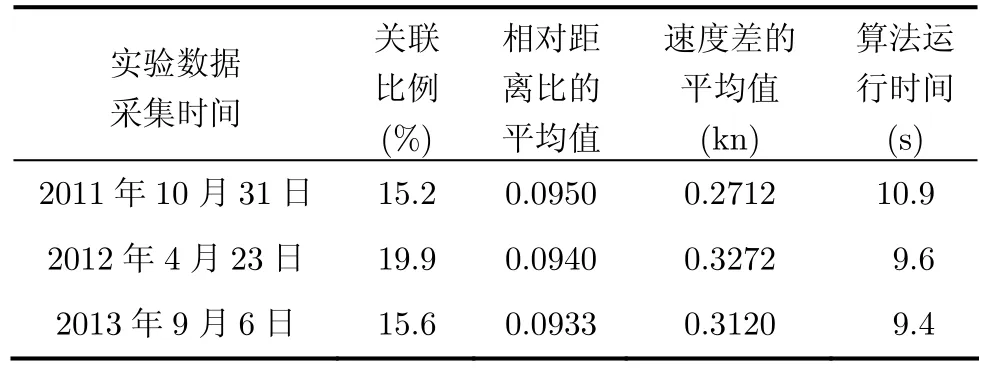
表5 不同获取时刻的数据关联情况

[1] Dobson C, Holenstein K, Smith M, et al.. Monostatic vessel detection statistics from the CODAR SeaSonde[C]. Proceedings of the OCEANS 2013 MTS/IEEE Conference, San Diego, United States, 2013: 1-4.

[2] Ji Y G, Zhang J, Meng J M, et al.. Point association analysis of vessel targets detection with SAR, HFSWR and AIS[J]. Acta Oceanologica Sinica, 2014, 33(9): 73-81.

[3] Habtemariam B K, Tharmarasa R, Meger E, et al.. Measurement level AIS/radar fusion for maritime surveillance[C]. Proceedings of the SPIE Defense, Security, and Sensing symposium, Maryland, USA, 2012, 83930I: 1-8.

[4] Chen J and Xie L. Research of Kalman filtering in shiptrack[C]. Proceedings of the 2nd International Conference on Transportation Information and Safety: Improving Multimodal Transportation Systems-Information, Safety, and Integration, Wuhan, China, 2013: 2464-2469.

[5] Gurgel K W, Schlick T, Horstmann J, et al.. Evaluation of an HF-radar Ship detection and tracking algorithm by comparison to AIS and SAR data[C]. Proceedings of the International Waterside Security Conference (WSS), Marina di Carrara, Italy, 2010: 1-6.

[6] Kazimierski W and Stateczny A. Fusion of data from AIS and tracking radar for the needs of ECDIS[C]. Proceedings of the Signal Processing Symposium, 2013, Serock, Poland, 2013: 1-6.

[7] Dzvonkovskaya A and Rohling H. HF radar performance analysis based on AIS ship information[C]. Proceedings of the 2010 IEEE Radar Conference, Washington DC, USA, 2010: 1239-1244.

[8] Hu X R and Lin C C. A preliminary study on targets association algorithm of radar and AIS using BP neural network[J]. Procedia Engineering, 2011, 15: 1441-1445.

[9] Liu C, Lin B, Liu X M, et al.. Fuzzy correlation algorithm for multi-target fusion of automatic identification system and radar[J]. Journal of Computational and Theoretical Nanoscience, 2013, 10(12): 2826-2830.

[10] Kazimierski W. Problems of data fusion of tracking radar and AIS for the needs of integrated navigation systems at sea[C]. Proceedings of the 14th International Radar Symposium, Dresden, Germany, 2013: 270-275.

[11] 田文龙, 李高鹏, 许荣庆. 利用自动识别系统信息进行高频地波雷达天线阵校正[J]. 电子与信息学报, 2012, 34(5): 1065-1069.

Tian W L, Li G P, and Xu R Q. High frequency surface wave radar antenna array alibration using automatic identification system data[J]. Journal of Electronics & Information Technology, 2012, 34(5): 1065-1069.

[12] 纪永刚, 张杰, 王祎鸣, 等. 双频率高频地波雷达船只目标点迹关联与融合处理[J]. 系统工程与电子技术, 2014, 36(2): 266-271.

Ji Y G, Zhang J, Wang Y M, et al.. Ship detection point association surface and fusion with dual-frequency HF wave radar[J]. Systems Engineering and Electronics, 2014, 36(2): 266-271.

[13] 盛卫东, 林两魁, 安玮, 等. 基于全局最优的被动多传感器多目标轨迹关联算法[J]. 电子与信息学报, 2010, 32(7): 1621-1625.

Sheng W D, Lin L K, An W, et al.. A passive multisensor multitarget track association algorithm based on global optimization[J]. Journal of Electronics & Information Technology, 2010, 32(7): 1621-1625.

[14] Kadar I, Eadan E R, and Gassner R R. Comparison of robustized assignment algorithms[C]. Proceedings of the Aerospace Defence Sensing and Control (AeroSense) Conference, Orlando, FL, USA, 1997: 240-249.

[15] Jonker R and Volgenant A. A shortest augmenting path algorithm for dense and sparse linear assignment problems[J]. Computing, 1987, 38(4): 325-340.

[16] Malkoff D B. Evaluation of the Jonker-Volgenant-Castanon (JVC) assignment algorithm for track association[C]. Proceedings of the Aerospace Defence Sensing and Control (AeroSense) Conference, Orlando, FL, USA, 1997: 228-239.

张 晖： 男，1983年生，博士生，研究方向为图像处理、多传感器数据融合等.

刘永信： 男，1955年生，教授，研究方向为图像处理、多传感器数据融合等.

张 杰： 男，1963年生，研究员，研究方向为海洋遥感探测等.

Target Point Tracks Optimal Association Algorithm with Surface Wave Radar and Automatic Identification System

Zhang Hui①Liu Yong-xin①Zhang Jie②Ji Yong-gang②Zheng Zhi-qiang①

①(College of Electronic Information Engineering, Inner Mongolia University, Hohhot 010021, China)
②(First Institute of Oceanography, State Oceanic Administration, Qingdao 266061, China)

In order to solve the problem that of High Frequency Surface Wave Radar (HFSWR) and Automatic Identification System (AIS) target point tracks fusion, a point tracks association algorithm using Jonker-Volgenant-Castanon (JVC) global optimal matching for different status is proposed. Firstly, the HFSWR and AIS target point tracks are divided into the quasi-static and dynamic data by the radial velocity. Then the radial velocity and spherical distance are selected as the feature parameters, and the different status data are respectively pre-associated by the radial velocity and spherical distance. Finally, the average of relative distance ratio is used to evaluate the effect of association. According to the selection of threshold parameter, the HFSWR and AIS point tracks are optimal associated with the JVC algorithm. The experimental results indicate that the proposed algorithm, in the condition of equal number point tracks associated, is superior to the Nearest Neighbor (NN) algorithm and Munkres association algorithm in the association accuracy, and the associate time is less than the NN algorithm and Munkres association. Moreover, three different time data gained from the target traits measured in nearly three years demonstrate that the feasibility and real-time of the proposed method.

High Frequency Surface Wave Radar (HFSWR); Automatic Identification System (AIS); Data association; Optimal association; Jonker-Volgenant-Castanon (JVC) algorithm

TN958

A

1009-5896(2015)03-0619-06

10.11999/JEIT140678

2014-05-21收到，2014-09-22改回

国家自然科学基金(61362002)和海洋公益性科研专项(200905029)资助课题

*通信作者：刘永信 yxliu@imu.edu.cn