基于双本振同步Nyguist折叠接收机的多分量LFM信号检测及参数估计

李 睿 陈殿仁

(长春理工大学电子信息工程学院 长春 130022)

基于双本振同步Nyguist折叠接收机的多分量LFM信号检测及参数估计

李 睿 陈殿仁*

(长春理工大学电子信息工程学院 长春 130022)

Nyquist折叠接收机(NYFR)为一种新颖的超宽带接收机结构，它可以利用单片ADC实现超宽带范围内信号的采集，而同步Nyquist折叠接收机(SNYFR)为其一种改进结构。该文在此基础上提出一种新的基于双本振方案的SNYFR结构，推导了多分量LFM输入下的数学模型。并基于此结构，提出一种基于正弦调频匹配(SFMM)与分数阶域折叠补偿相结合的多分量LFM信号奈奎斯特区域(NZ)判定与参数估计算法，克服了单本振SNYFR结构处理多分量LFM输入时的困难，提高了NZ判定及参数估计的抗噪声性能。计算机仿真表明，该文算法可以有效地对多分量LFM信号进行检测并实现各分量参数的高精度估计。

超宽带接收机；奈奎斯特折叠接收机；正弦调频匹配；分数阶傅里叶变换

1 引言

超宽带接收机需要在极宽的带宽范围内实现输入信号的高概率接收。而受限于当前ADC器件的发展水平，无法依靠单片高性能的ADC完成超宽带信号的采集[1]。传统的解决方案一般采用时间交替多通道并行采样[2]，基于滤波器组的信道化数据采集[3,4]以及基于信号基展开[5]等技术实现超宽带信号的采样。受压缩感知理论启发，文献[6,7]提出了Nyquist折叠接收机(NYguist Folding Receiver,NYFR)结构，实现了单片ADC对超宽带信号的无失真采样。针对该结构，文献[8]利用了正交匹配追踪(Orthogonal Matching Pursuit, OMP)、迭代贪婪展开(Iterative Greedy Unfolding, IGU)等算法恢复原始信号，但运算量较大。文献[9]采用小波分析方法处理折叠信号，简化了计算，更易工程实现。文献[10]提出了基于周期线性调频(LFM)本振的同步奈奎斯特折叠接收机(SNYFR)，该结构用数字合成的多分量周期LFM本振代替全模拟结构产生的本振信号，克服了NYFR在本振调制时刻易受噪声影响及不能提取初始相位信息等缺点。文献[11]引入编码机制，以调制带宽固定但编码信息不同的调制本振分量划分奈奎斯特区域(Nyquist Zone, NZ)，扩展了监测带宽范围，但其基于伪魏格纳分布(PWVD)的参数估计算法在处理多分量信号时存在交叉项。文献[12]采用正弦调频(SFM)的本振信号，给出了单分量LFM输入下的NZ检测及参数估计算法。然而，该算法需要先对折叠信号样本按本振调制周期进行再抽取，未有效利用原始样本的所有信息，抗噪声性能不够理想。并且该算法在进行折叠信号的NZ检测时需遍历NZ函数的所有可能取值，在输入为多分量LFM信号时，由于NZ函数在同一时刻的多值性，该算法将不再适用。

本文为解决SNYFR处理多分量LFM信号的困难，提出了一种基于正弦调频(SFM)本振的双路SNYFR结构。给出了输入为多分量LFM信号时的信号流程。并提出了基于正弦调频匹配(Sinusoidal Frequency Modulation Matching, SFMM)与分数阶域折叠补偿相结合的NZ判定与参数估计算法。最后用计算机仿真验证了算法的正确性及有效性。

2 双本振SNYFR及多分量LFM信号流程

双本振SNYFR接收机结构如图1所示。可以看出，该结构在原型结构[10]基础上增加了一个支路。其中，LPF1为超宽带预选低通滤波器，用以滤除带外噪声，其带宽为B。为推导方便，假设原始输入为I, Q两路相互正交的信号。则当输入r( t)为多分量LFM信号时有其中，lA,fl,Kl及φl分别为第l个分量的幅度、初始频率、调频率及初始相位。本振合成模块生成的两路本振信号分别为

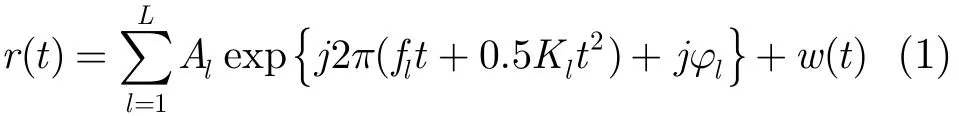
图1 双本振SNYFR接收机结构

可以看出，两路本振信号都含有M个分量，且相邻分量频谱的中心频率间隔为fs。不同的是，式(2)的各个分量都是正弦调频(SMF)的，其调制频偏为固定值u0，调制频率为vm(m=1,2,…,M)。而式(3)则为M分量的单频信号。这样，两路本振将频率轴划分成M个以fs/2+mfs为中心，带宽为fs的奈奎斯特区域(NZ)，如图2所示。这两路本振信号可由本振合成模块中的多通道DDS分别合成各个正弦及SFM分量再经过倍频混频阵列[10]生成，且所有DDS都采用同一个参考信号以保证各分量的初相一致(本文为推导方便令初相为0)。r( t)经功分后，分别与式(2)与式(3)混频并经过通带为的复低通滤波器LPF2得到两路折叠信号：

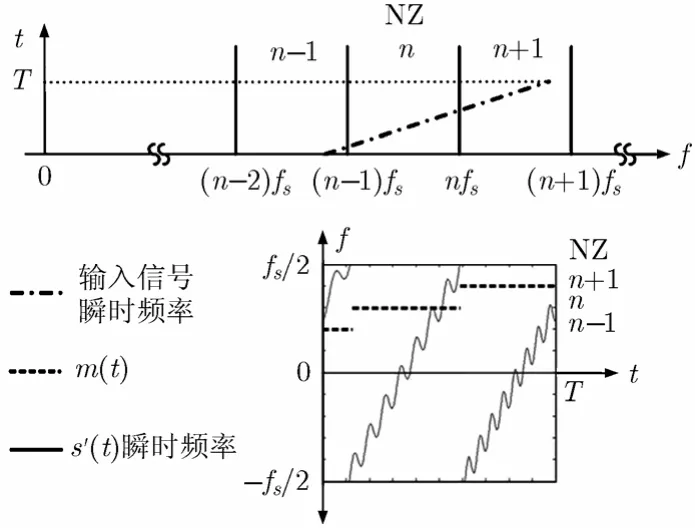
图2 输入为LFM信号的折叠过程

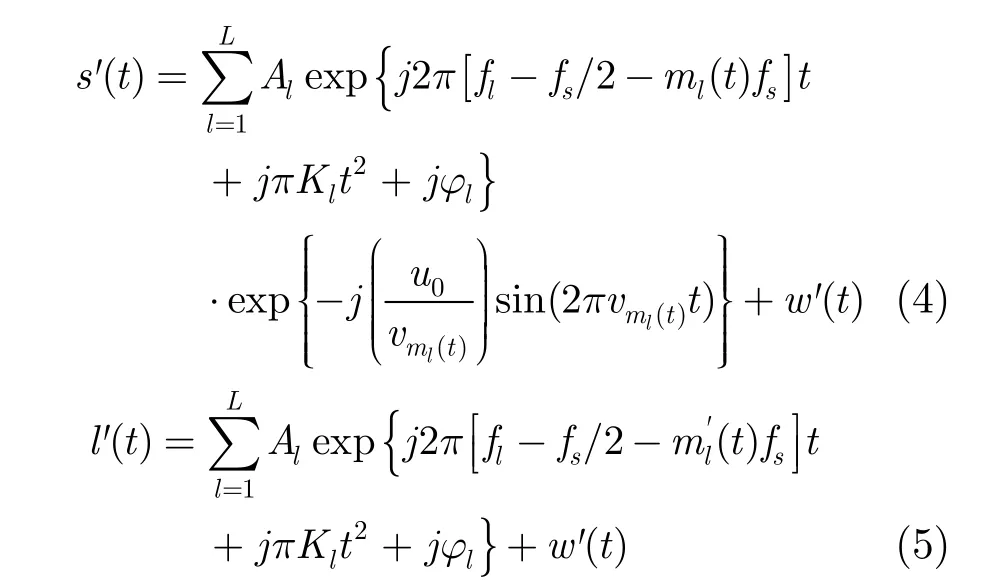
式(4)和式(5)中，w′(t)由输入信号的噪声与本振信号混频产生，仍可视为白噪声，为后面推导方便忽略其影响，定义ml( t)与分别为输入信号在本振p1( t)与p2( t)下的NZ函数，表示为

若u0＜＜fs，可近似认为ml( t)≈。图2为频谱跨越3个NZ的LFM分量的时频曲线经折叠得到s′( t)的过程示意图。从式(4)及图2可以看出，分布于不同NZ的输入信号分量的频谱都被折叠到的范围内，且其正弦调频部分的调制频率与m( t)的取值一一对应，而m( t)的取值又与输入分量频谱所处的NZ相对应。因此只要先通过调制频率检测m( t)的取值，即可实现NZ判定。再结合折叠信号分量的参数估计便可间接得到对应的输入LFM信号分量的参数估计值。

虽然式(4)包含输入分量的全部信息，但由于其分量为复合调制信号，很难直接处理，在多分量的情况下则更为复杂。因此考虑引入一个辅助信号简化NZ判定。将式(4)和式(5)经采样率为fs的ADC采样后送入DSP进行共轭相乘计算，得到辅助信号：

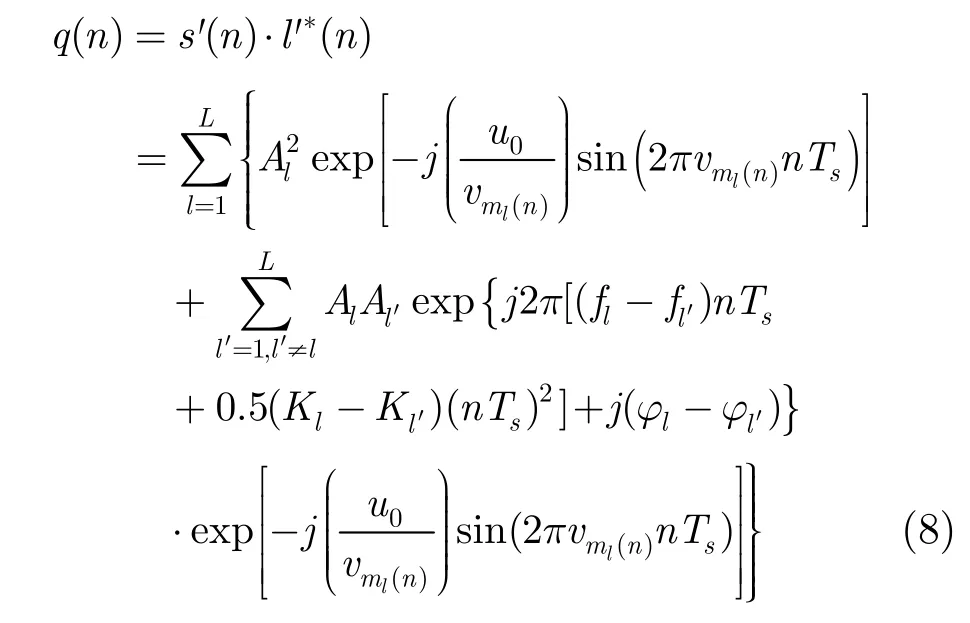
由式(8)可以看出，q( n)共包含L2项，其中L项为中心频率为0，调制带宽为2u0的正弦调频信号，由与输入分量rl( t)对应的两个折叠分量的共轭乘积产生，定义为自项。其各自的调制频率vml ( n )与该分量对应的离散NZ函数ml( n)一一对应。其余L2-L项为不同输入分量对应的折叠信号间的乘积，仍然为复合调制信号。因此，通过检测自相调制频率vml ( n )即可间接实现NZ判定。考虑到双路结构可能出现的不一致性问题，还加入了幅度比较及增益控制环节，以保持双路信号的幅度基本相同，从而保证后面算法的可实现性。

3 多分量LFM信号NZ判定与参数估计

3.1 基于SFMM的NZ判定

定义离散信号x( n)的N点SFMM为式中，u0为恒定值；0＜v≤N。则式(8)分量qk( n) 的SFMM为其中，

n2]内取值为vmk，则当v=vmk时，

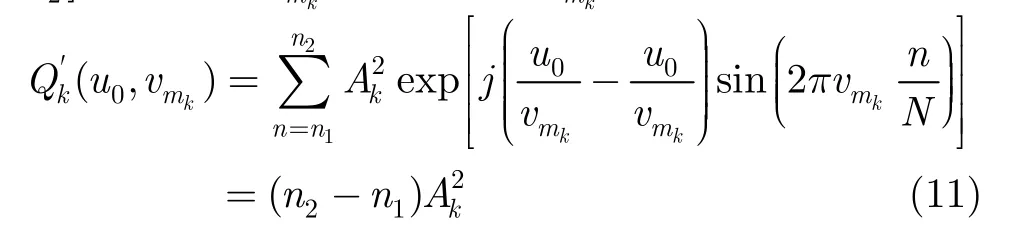
当v≠vmk时，根据恒等式：

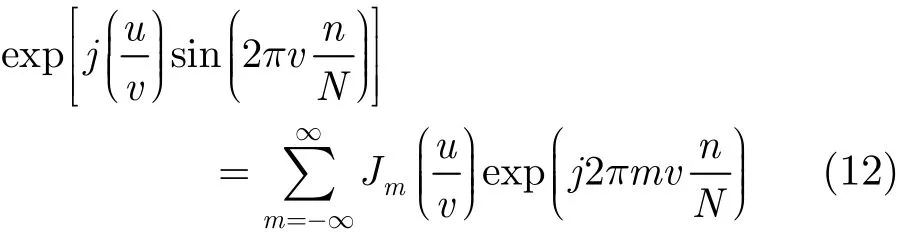
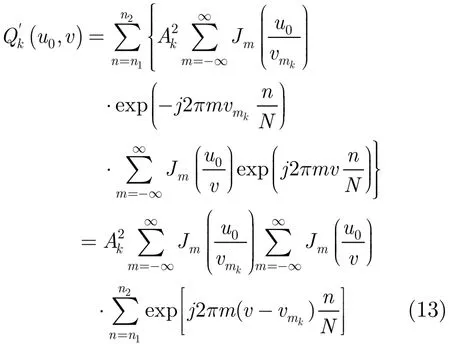
由于v-vmk≠0，则式(13)中，

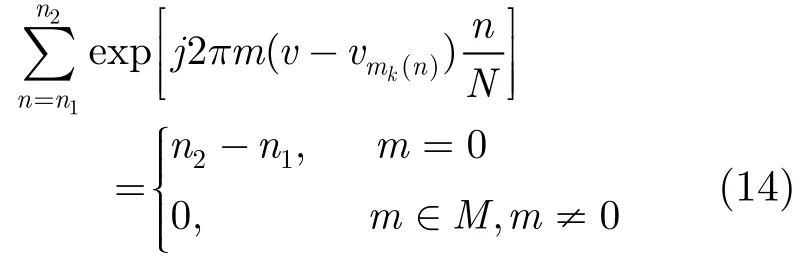
所以有

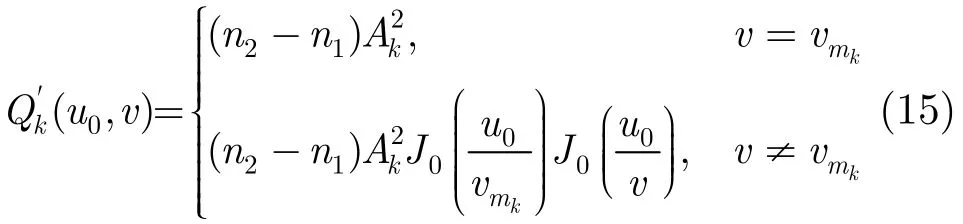
同理，对于Wk( u0, v)，当v≠vmk时，

式(17)中Δflk,ΔKlk不同时为0，因式(17)中下划线部分为一个LFM信号或一个频率非零的单频信号对时间求和，若Δflk或ΔKlk的值足够大(大于算法最小分辨率)，和值将远小于SFMM产生的峰值，可近似视为0。由此可以得到

综上：Qk(u0, v)只有在v等于自项中的某个取值时才呈现匹配峰值，而在其他情况下几乎为0。由于q( n)为L个形式与式qk( n)相同分量的叠加，q( n)的SFMMQ( u0, v)将会在v=vml(n)(l=1,2, …,L )处出现峰值，而在其它值时近似为0。因此只要在v∈vm(m=1,2,…,M)上对Q( u0, v)进行1维峰值搜索即可实现输入分量的NZ判定。

3.2 基于分数阶域折叠补偿的参数估计算法

作为Fourier变换的广义形式，信号的分数阶傅里叶变换(FRFT)可以解释为将坐标轴在时频平面上绕原点以角度α做逆时针旋转，十分适合处理LFM类信号，并且在处理多分量信号时不存在交叉项。

假设Q( u0, v)最大峰值处对应NZ函数的取值为mmax，且输入分量rk( t)与该取值对应部分的范围为[n1, n2]。根据mmax对应的本振调制频率vmmax生成本地信号：

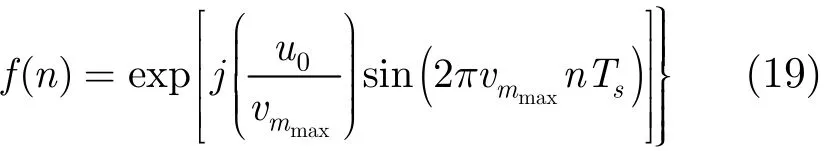
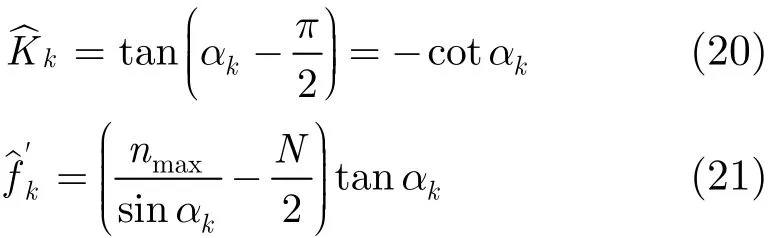
为减小计算量，本文采用了文献[13]介绍的方法对变量(α,n)进行迭代搜索，并采用Clean算法来消除强弱分量及多峰值间的干扰。

4 算法仿真与分析

设接收机监测带宽B=10 GHz ，所有仿真的输入信号样本长度T=1 μs , ADC采样频率fs= 1 GHz。所有仿真的Monte Carlo实验次数为500。

4.1单分量LFM信号NZ判定性能

设输入信号为单位幅度的单分量LFM信号，参数初始频率及初始相位别为1.25 GHz及π/6。SFM本振调制频偏u0=30 MHz ，调制频率vm为从1 MHz起始，间隔为Δv =0.5 MHz的10个取值。

本文采用正确检测概率(Probability of Correct Decision, PCD)衡量NZ判定性能，其定义为：算法正确判定NZ取值，并以此得到正确参数估计的次数与总实验次数的比值。图3表示当调频率K分别时的PCD随SNR的变化曲线。加入文献[12]中方法的PCD作为对比可知，由于本文方法利用了所有样本的信息因此在K较小时，PCD在SNR为-7 dB即可达到100%，抗噪声性能明显更优越。而当K较大时，输入LFM信号的频谱跨越多个NZ，折叠信号分段增加，以至信号能量分散，判定性能下降。考虑到实际应用中LFM信号调制带宽大多为百兆数量级，因此本文算法实用性更好。

4.2 多分量LFM信号NZ判定性能与本振调制参数的关系

为考察多分量LFM信号输入下的NZ判定性能，设输入信号中同时存在3个LFM分量，它们的幅度、初始频率、调频率及初始相位分别为：(1)/5}，其中分量(1)频谱跨越3个NZ，但其频谱能量主要分布于NZ=2。设定以保证本振分量在样本时间内至少存在一个完整的调制周期，令Δv =0.5 MHz。则其折叠信号的SFMM如图4所示，可以看到，各分量对应的NZ处都产生了明显峰值，峰值大小与信号分量的幅度强弱相对应。由于分量(1)跨越3个NZ，所以NZ函数在3个取样点处都产生了峰值，其中NZ=2处峰值最大。

为考察u0取不同值时对NZ判定性能的影响，定义PCD为算法按信号分量的幅度大小依次正确判定各分量的NZ取值并得到正确参数估计的次数与试验次数之比。图5为PCD与信噪比的关系(输入信噪比以输入信号中最弱分量(2)为标准)，可以看出u0取值过小(20 MHz)或过大(150 MHz)都会造成判定性能严重恶化。这是由于当u0取值过小时，式(18)中u0/vm的值变小使得SFMM峰值外衰减变得缓慢，分辨力减弱，SFMM的结果在相邻的取值上可能出现错误的峰值。同时，过小的调制频偏使得本振调制深度不足，抗噪声性能减弱，也会使判定错误的几率上升。当信噪比升高时，虽然噪声对调制的影响减弱，但是若存在峰值判定错误造成的误判，噪声的减小则反而会使出现错误的几率上升，PCD随信噪比的增加呈下降趋势。而当u0取值过大时，的近似不再成立，若信号分量的频谱分布接近NZ边界，则其折叠信号的NZ函数m( t)在折叠带宽边界处的取值可能发生错误的跳变，经SFMM后也会产生错误的峰值导致NZ判定出错。并且u0取值的增大会使迭代消去时的遮蔽带宽变宽，使下一次迭代的信号能量损失增加，同样影响判定性能。因此，建议将u0的取值设定在采样频率fs的3%～10%范围内。

4.3 参数估计性能

在得到输入分量NZ信息后，利用3.2节提出的算法对待估计信号g( n)进行参数估计。由于调频率的估计精度直接影响分量各参数的估计精度，因此本文仅以调频率估计为例讨论u0的选择对估计精度的影响。图6给出了不同u0时，各分量调频率估计的归一化均方误差(NMSE)随信噪比的变化情况(为消除栅栏效应采用了文献[14]中介绍的插值方法)，并与克拉美–罗界(CRB)进行比较。可以看出，由于分量(3)跨越3个NZ，能量在频域上较分散。受NZ判定性能影响，u0的变化对其影响最明显，u0过大或过小都造成其参数估计精度的恶化。分量(1)与分量(2)在u0的各个实验取值下都达到了一定的精度，但在u0取值较为合适的情况下信噪比门限值更低且估计精度更高。由此可见，输入分量频谱的宽度对NZ检测性能的影响将直接反映在参数估计的性能上。当分量频谱存在跨NZ情况时，其带宽越大，能量在频域越分散，在相同的条件下，其对应的参数估计性能也越差。

5 结束语

本文给出了一种新的双本振SNYFR结构，利用两路折叠信号的相似对消性质，提出了正弦调频匹配(SFMM)算法，实现了超宽带范围内多分量LFM信号的NZ判定，并且只需在预先设定的调制频率点上进行1次搜索即可完成各分量的NZ判定，计算简便且具有较好的抗噪声能力。同时提出的基于分数阶域折叠补偿的参数估计算法利用迭代消去的方法依次得到各分量主要参数估计值。在信噪比满足要求的情况下具有较高的估计精度，具有一定的工程及理论参考价值。

针对算法对较弱分量存在参数估计精度下降的不足。下一步的工作为改进算法，减小信号分量间的影响，提高参数估计精度。另外，本振信号的具体实现方式也需要进一步研究。

图3 单分量LFM信号NZ判定PCD与SNR的关系

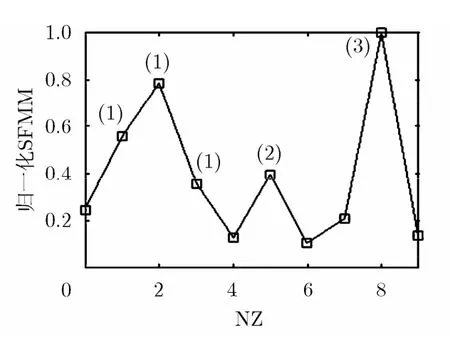
图4 多分量LFM信号的 SFMM在各NZ处的值

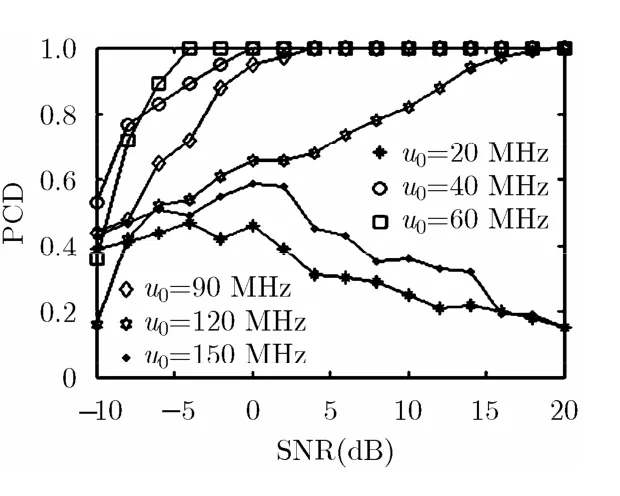
图5 多分量LFM信号NZ判 定PCD与SNR的关系

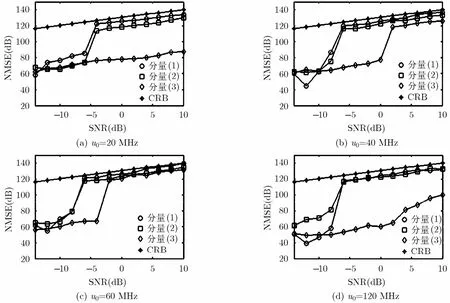
图6 不同u0时调频率的估计精度随SNR变化曲线

[1] 曾德国. 低截获概率雷达信号侦收技术研究[D]. [博士论文],电子科技大学, 2012. Zeng De-guo. Study on the interception of low probability of intercept radar signals[D]. [Ph.D. dissertation], University of Electronic Science and Technology of China, 2012.

[2] 张俊杰, 武杰, 刘尉悦, 等. 高速交替/并行数据采集系统时钟研究[J]. 中国科学技术大学学报, 2006, 36(3): 281-284. Zhang Jun-jie, Wu Jie, Liu Wei-yue, et al.. Clock study of high speed interleaving/multiplexing data-acquisition system [J]. Journal of University of Science and Technology of China, 2006, 36(3): 281-284.

[3] Velazquez R, Nguyen Q, Broadstone R, et al.. Design of hybrid filter banks for analog/digital conversation[J]. IEEE Transactions on Signal Processing, 1998, 46(4): 956-967.

[4] Namgoong A. Channelized digital ultra wideband receiver[J]. IEEE Transactions on Wireless Communications, 2003, 2(3): 502-510.

[5] Hoyos S, Sadler M, and Arce R. Ultra-wideband analog-todigital conversion via signal expansion[J]. IEEE Transactions on Vehicular Technology, 2005, 54(5): 1609-1622.

[6] Fudge L, Bland E, Chivers A, et al.. A Nyquist folding analog-to-information receiver[C]. 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, 2008: 541-545.

[7] Pace E, Kusmanoff A, and Fudge, L. Nyquist folding analogto-information receiver: autonomous information recovery using quadrature mirror filtering[C]. 43rd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, 2009: 1581-1585.

[8] Ray M, Gerald L. Fudge L, et al.. Analog-to-information and the Nyquist folding receiver[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2012, 2(3): 564-578.

[9] Olusegun O, Cajetan M, Gerald F, et al.. Application of analytic wavelet transform for signal detection in Nyquist folding analog-to-information receiver[C]. IEEE International Conference on Communications, Dresden, 2009: 1-5.

[10] 曾德国, 成昊, 唐斌, 等. 基于周期LFM本振的同步Nyquist折叠接收机多分量信号参数估计算法[J]. 航空学报, 2012, 33(4): 688-695. Zeng De-guo, Cheng Hao, Tang Bin, et al.. Parameter estimation approach for multicomponent signals intercepted by synchronous Nyquist folding receiver using local periodic LFM signals[J]. Acta Astronautica Sinica, 2012, 33(4): 688-695.

[11] Ke Yu-long. Intercept of frequency agility signal using coding Nyquist folding receiver[J]. WSRAS Transations on Signal Processing, 2011, 7(2): 82-91.

[12] 曾德国, 祝俊, 唐斌. 左边带本振SNYFR接收的LFM信号参数估计算法[J]. 宇航学报, 2012, 33(6): 781-787. Zeng De-guo, Zhu Jun, and Tang Bin. Parameter estimation of LFM signal intercepted by left sideband Synchronous Nyquist Folding Receiver[J]. Journal of Astronautics, 2012, 33(6): 781-787.

[13] 齐林, 陶然, 周思勇, 等. 基于分数阶Fourier变换的多分量LFM信号的检测和参数估计[J]. 中国科学(E辑), 2003, 33(8): 749-759. Qi Lin, Tao Ran, Zhou Si-yong, et al.. Multi-component LFM signal detection and parameter estimation based on fractional Fourier transform[J]. SCIENCE IN CHINA (Series E), 2003, 33(8): 749-759.

[14] 宋军, 刘渝, 刘云飞. LFM信号参数估计的插值FrFT修正算法[J]. 信号处理, 2012, 28(1): 112-117. Song Jun, Liu Yu, and Liu Yun-fei. Modified interpolation parameters estimation for LFM signals based on FrFT[J]. Signal Processing, 2012, 28(1): 112-117.

李 睿： 男，1985年生，博士生，研究方向为信号处理.

陈殿仁： 男，1952年生，教授，主要从事雷达系统及雷达信号处理方面的研究.

Multi-component LFM Signal Detection and Parameter Estimation Algorithm Based on Synchronous Nyquist Folding Receiver with Dual Local Oscillator

Li Rui Chen Dian-ren
(School of Electronics and Information Engineering, Changchun University of Science and Technology, Changchun 130022, China)

NYquist Folding Receiver (NYFR) is a novel ultra-wideband receiver structure, which can sample a large range wideband signal by using a single ADC. The Synchronous NYquist Folding Receiver (SNYFR) is an improved structure of NYFR. In this paper, a new SNYFR structure with dual local oscillator is proposed and its mathematical model with the input of multi-component LFM signal is deduced. meanwhile, under the input of multi-component LFM signal, a Nyquist Zone (NZ) judgment and parameters estimation algorithm based on combination of Sinusoidal Frequency Modulation Matching (SFMM) and fractional domain folding compensation is proposed to overcome the difficulties of single local oscillator SNYFR structure in dealing with multi-component LFM signal and to improve noise immunity. Computer simulations show that effective detection of multicomponent LFM signal and accurate parameters estimation can be achieved by using the proposed algorithm.

UWB receiver; NYquist Folding Receiver (NYFR); Sinusoidal Frequency Modulation Matching (SFMM); FRactional Fourier Transform (FRFT)

TN971.1

A

1009-5896(2015)01-0091-06

10.11999/JEIT140281

2014-03-15收到，2014-07-16改回

*通信作者：陈殿仁 dianrenchen@cust.edu.cn