基于拓扑统计距离的航迹抗差关联算法

董 凯王海鹏 刘 瑜

(海军航空工程学院信息融合研究所 烟台 264001)

基于拓扑统计距离的航迹抗差关联算法

董 凯*王海鹏 刘 瑜

(海军航空工程学院信息融合研究所 烟台 264001)

传感器观测目标的拓扑信息可用于解决系统误差下的航迹关联问题，但传统方法对航迹信息利用不足且难以适应传感器虚警和漏报的情形。论文提出一种基于拓扑统计距离的航迹抗差关联算法，首先转换目标状态估计及其协方差以得到目标参照系下的拓扑描述；然后在推导拓扑统计距离的基础上，进行全局最优关联；最后以目标参照系下邻居目标关联对的平均统计距离作为参照目标间的关联度，根据双门限准则完成参照目标的关联判决。仿真结果表明，在密集编队目标、随机分布目标和传感器存在虚警漏报条件下，该算法的性能明显优于传统方法。

航迹关联；系统误差；拓扑统计距离；抗差

1 引言

在实际工程应用中，传感器本身在测量过程中常常会累积系统误差(如距离、方位、俯仰测量系统误差)，另外传感器的载体平台，如舰艇、飞机等，运动过程中导航系统也会引入定位误差，经常性的系统标校不能彻底解决该问题。系统误差使传感器的观测航迹整体偏离目标真实轨迹，当分布式多传感器航迹关联与融合时，融合中心的航迹关联难以根据位置信息去除重复航迹，导致虚假航迹的出现[1- 3]。然而，虽然传感器的系统误差改变了目标观测的绝对位置，但是对目标间的相对位置关系影响不大，即观测目标的拓扑结构差别不大[4]，为利用目标拓扑信息进行航迹关联提供了可能。

针对存在系统误差条件下的航迹关联问题(本文称之为航迹抗差关联问题)，人们从利用目标拓扑信息的角度进行了一些有益的研究[5- 7]，但大多没有考虑传感器的虚警和漏报问题，即假设各传感器共同观测所有目标。文献[8]分析了传感器虚警和漏报导致拓扑结构成员个数不一致的问题，并给出了初步的估计判别方法；文献[9]做了进一步改进，根据目标点对的欧式距离建立匹配支持度，采用松弛迭代的方法逐步选取平均匹配支持度最大的目标对为匹配目标点对，但该方法将系统误差的影响近似为平移效应，忽略方位系统引入的旋转效应，限制了算法的适用范围；文献[10]针对此问题以目标航向为参照将拓扑空间划分为多个象限，根据各象限内目标径向距离之和的拓扑向量、航速欧式距离和航向变化率3个模糊因素集建立综合相似度以进行关联判决，但象限划分受到目标航向随机误差的影响，并且传感器的虚警和漏报将进一步降低拓扑相似度。此外这些拓扑类方法往往仅利用了航迹的位置信息，因此本文利用航迹状态估计及其协方差信息，提出一种基于拓扑统计距离的航迹抗差关联算法，推导了目标参照系下拓扑描述和拓扑统计距离航迹关联模型，并针对虚警和漏报情形采用拓扑结构部分匹配模型和双门限准则实现航迹抗差关联。

2 系统模型描述

2.1 系统误差影响分析

假设两部2维传感器对目标进行跟踪观测，相应的航迹集合分别为

式中，n1和n2分别为两传感器的观测航迹数。定义k时刻传感器1和传感器2的航迹数据在公共直角坐标系下第i和第j条航迹的状态估计分别为和(为简便起见，略去时间下标k)，对应的估计协方差为P1i和P2j。

通常认为传感器系统误差为较小常量或者长时间范围内的缓变量，因此在一定观测时间内可以视为常量。设真实目标的距离和方位分别为r和θ，不考虑随机量测误差时，传感器方位和距离系统误差分别使目标观测值偏离Δθ角度和Δr距离，即在系统误差影响下，所有目标的观测值在传感器极坐标系下相对目标真实位置发生Δθ的旋转和Δr的伸缩。文献[10]的推导表明，当目标观测区域距离传感器较远时(Δr/ r≪1)，可忽略距离系统误差引起的仿射变换，近似认为传感器的系统误差不改变各目标之间的相对位置关系，即一部传感器的航迹经过整体旋转和平移后能够与另一部传感器的航迹重合。这在实际上通常也是容易满足的(如：r≥50 km, Δr ≤1 km)。

2.2 目标参照系下的拓扑描述

在传感器方位系统误差影响下，传感器观测目标的拓扑结构隐含方位系统误差，而传感器滤波得到的目标航向也包含方位系统误差，因此如果以观测目标位置为原点，其航向为参照方向建立目标参照系，可以抵消方位系统误差。因此，本文在目标参照系下对目标拓扑结构进行描述，将传感器局部坐标系下的目标数据转换至目标参照系下。以传感器1航迹数据转换过程为例，将原状态估计及其协方差转换到目标u(u=1,2,…,n1)的参照系下(目标u本身数据也需转换)，设转换后u的邻居目标i(i=1,2,…,n1)对应的状态估计及其协方差分别为

式中，T1(u)为旋转矩阵，与目标u的航向有关。

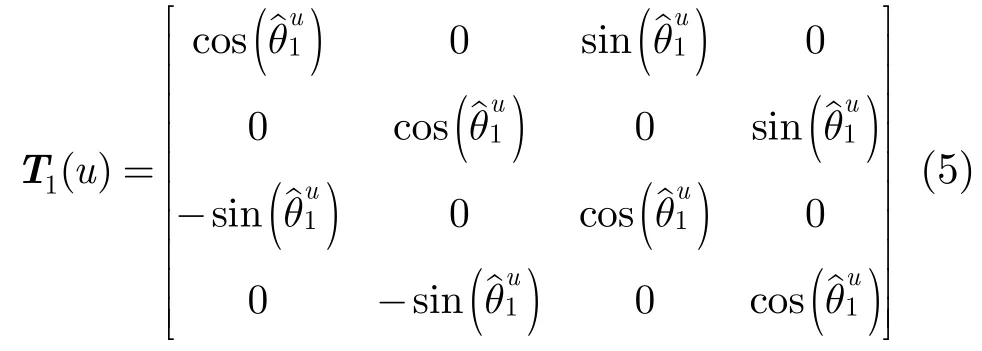
同理，将传感器2局部坐标系下n2个目标数据转换到目标v(v=1,2,…, n2)参照系下(目标v本身的数据也需转换)，设转换后v的邻居目标j(j=1,2,…, n2)对应的状态估计和误差协方差分别为和。

3 算法描述

3.1 基于拓扑统计距离的全局最优关联判决

当传感器对目标滤波稳定收敛时，随机误差相对系统误差较小，如果忽略由此引入的参照目标航向误差，则各传感器关于同一目标的参照系是统一的。由于统计距离利用了状态估计协方差信息，从概率意义上比欧式距离更准确，因此结合式(3)和式(4)可得传感器1的目标u和传感器2的目标v参照系下目标i和目标j之间的统计距离γij(u, v )为

式中，Δij(u, v )为传感器1的目标i和传感器2的目标j的状态估计之差，Bij(u, v )为对应的状态估计协方差。然后以统计距离γij(u, v)为航迹关联检验统计量，在自由度为nx和显著性水平为α的χ2门限δ( α,nx)下进行航迹关联检验。

当参照目标航向估计误差不能忽略时，推导可得传感器1参照目标u航向估计值方差为

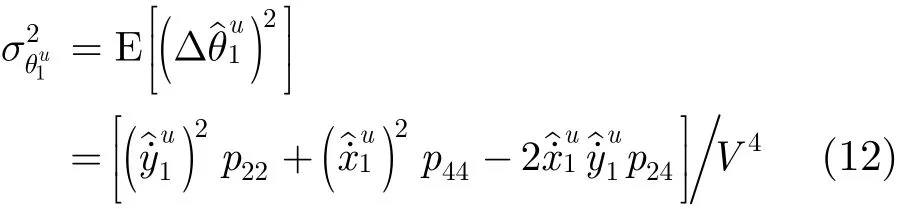
建立以统计距离γij(u, v )为统计量，L( k)为目标函数的2维分配模型[11,12]，求解全局最优的航迹关联关系：

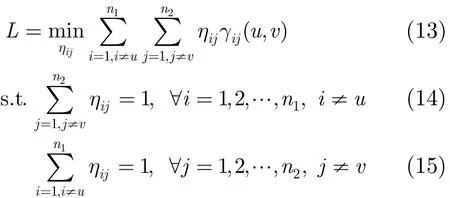
式中，ηij为二进制变量，ηij=1表示航迹i和航迹j来自于同一目标，ηij=0则表示来自于不同目标。2维分配得到的关联对再经过关联门限的检验，即统计距离低于门限的关联对才被确认为航迹关联对。2维分配问题的求解有多种方法，可采用效率较高的JVC算法[13]。

3.2 基于参照目标关联度的双门限关联准则

虚警和漏报问题将导致各传感器可能存在非共同观测目标，此时邻居目标的拓扑结构不一致，不能保证所有邻居目标被确认关联，因此根据k时刻的航迹关联结果，定义所有确认关联对的平均统计距离度量参照目标u和目标v的关联度：

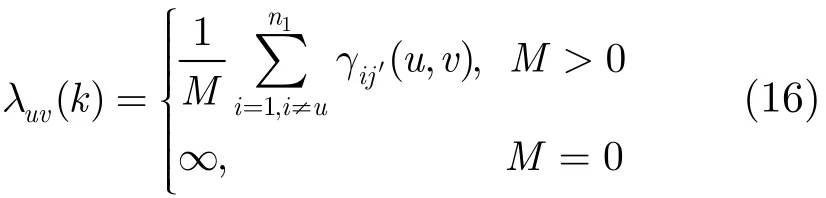
式中，j′表示与传感器1目标i确认关联的传感器2目标，M表示确认关联对的数量。λuv(k )越小，表明目标u和目标v的关联度越高，反之越低。当M=0时，表明在当前目标u和目标v的参照系下没有确认关联对，即目标u和目标v不是关联目标，此时λuv(k )可取任意足够大的值。由此可以计算得到k时刻传感器1 的n1个目标航迹和传感器2的n2个目标的关联度矩阵

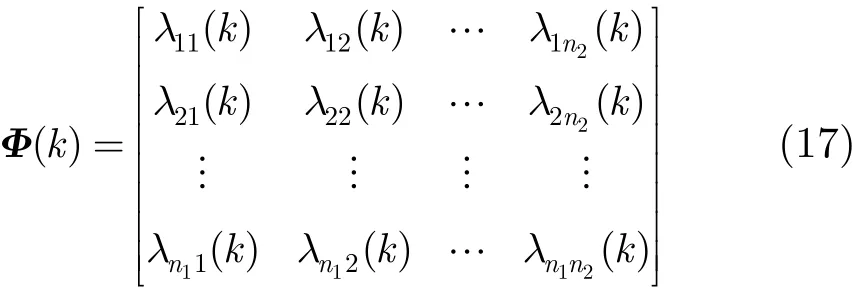
根据关联度矩阵Φ(k)，选取使λuv(k )达到最小对应的目标对为试验关联对。在单时刻试验判决的基础上，再利用多时刻的判决结果，采用双门限准则[14]进一步作出确认关联对的判决。选择正整数I 和R, ∀k=1,2,…,R 。若目标u和目标v′为试验关联成功，则设定航迹关联质量muv′(k)=muv′(k-1)+1, muv′(0)=0；当muv ′(k)≥I 时，则宣布传感器1的目标u与传感器2的目标v′为确认关联对；而如果∃u′∈U1对任意与其可能关联的v′均有 mu′v′(k) ＜I ，则需要在后续时刻继续进行关联判决；如果对于某一个目标u，使muv(k)≥I成立的v不止一个，则需进行多义性处理。

首先，选择使航迹关联质量最大的v′为确认关联对，即

但如果满足式(18)的目标v′仍不止一个，则选择使关联度量向量平均范数最小的目标对为确认关联对，即

由于传感器送到融合中心的航迹数据是逐个或逐批的，因而I和R数值的选择是动态的，例如可选1/1, 2/2, 2/3, 3/4, 3/5, 4/5, 4/6, 5/7, 6/8,…等准则。算法流程图如图1所示。

4 仿真分析

4.1 仿真环境

为验证算法性能，将本文的拓扑统计距离法和基于文献[9]的拓扑欧式距离法、文献[10]中拓扑模糊法进行对比。首先，为分析航向估计误差对航迹拓扑结构的影响，给出了如图2～图4所示仿真结果；然后在3个仿真环境下进行仿真，给出各算法航迹正确关联率Ec的对比结果，如图5～图7所示。仿真中均进行50次蒙特卡罗仿真，每次12步。两部传感器的坐标分别为(0, 0) km和(100, 0) km，测距随机误差均为100 m，测角随机误差均为0.3°，测距系统误差均为100 m，测角系统误差分别为2°和-2°，采样周期均为4 s。设置α=0.01, nx=4，拓扑模糊法的模糊因素展度和系数设置同文献[10]，划分象限数为16。为便于分析传感器的虚警和漏报对航迹关联正确率的影响，定义两部传感器对目标的共同观测率Pc为式中，两传感器的航迹集合U1和U2的交集表示共同观测目标，并集表示观测的所有目标，符号|·|表示计算集合元素的数量。可见，共同观测率指的是共同观测目标占所有观测目标的比例，虚警和漏报直接影响共同观测率。航迹正确关联率Ec的定义为：正确关联不同传感器航迹中源于相同目标航迹的概率，其计算过程为：正确关联航迹对的数量Nc与所有共同观测的目标航迹的比值，即

环境1：密集编队目标环境下，模拟30批目标在2维平面内匀速直线运动，第1个目标初始位置为(30, 20) km，其它目标在x方向上等距离间隔300 m，目标初始速度均为400 m/s，初始航迹向均为60°，两部传感器对目标的共同观测率Pc=1。

环境2：随机分布目标环境下，模拟30批目标在2维平面内匀速直线运动，各目标的初始位置在以(50, 50) km与(60, 60) km为对角顶点的矩形区域内按均匀分布产生，目标的初始速度和初始航向分别在150～220 m/s 和0～2π的范围内均匀分布。2部传感器对目标的共同观测率Pc=1。

图1 算法流程图

环境3：在环境2的基础上，设置两部传感器对目标的共同观测率Pc=0.5。

4.2 仿真结果与分析

图2为环境2下两部传感器关于同一目标的航向估计误差曲线，步数推进至4步以后航向估计误差小于0.1rad并继续收敛。如3.1节所述，针对航向估计误差的影响，对拓扑统计距离法和拓扑欧式距离法分别采用近似航迹抗差关联门限T1=同门限系数下的航迹正确关联率，如图3～图4所示。由图3可见，航向估计误差较大时，不同门限系数下的正确关联率差别较大，但随着航向估计误差的降低，不同门限系数下的正确关联率趋于一致，由图4也能得出类似结论，可知两种算法的门限系时关联性能已经十分接近。因此在后续仿真中，可取拓扑统计距离法的门限系数C1=20，拓扑欧式距离法的门限系数

图5为环境1下3种算法的航迹正确关联率比较图。从图5中可以看出，本文提出的拓扑统计距离法性能明显优于拓扑欧式距离法和拓扑模糊法，拓扑模糊法性能最差。分析其原因，一是拓扑统计距离度量比拓扑欧式距离度量更准确；二是编队目标的速度和航向等运动特性相似，导致拓扑模糊法中的速度和航向两个模糊因素失去对关联判决的作用，并且编队目标集中于根据算法要求划分的参照目标部分象限分界线附近，在随机误差影响下其相对拓扑向量的准确性大大降低，导致正确关联率较低。另外，由于编队目标平行运动，拓扑结构没有显著变化，所以3种算法的性能随步长推进而保持稳定。图6为环境2下3种算法的航迹正确关联率比较图。可见3种算法的性能均随步长推进逐步提高，其中拓扑模糊法性能最差，拓扑统计距离法和拓扑欧式距离法性能十分接近。主要原因是目标随机分布使不同参照目标的拓扑结构差异比较显著，并且随着步长推进，目标的密集程度进一步降低，使不同参照目标的拓扑结构差异性也进一步提高，再加上航迹滤波过程降低了参照目标航向误差，这些都有利于提高正确关联率。图7为环境3下3种算法航迹正确关联率比较图。与图6的区别在于，由于不同传感器对目标的共同观测率低，参照目标的拓扑结构相似度降低，拓扑统计距离法和拓扑欧式距离法考虑了这一情形，所以性能仅略有降低，影响较小，而拓扑模糊法性能受到较大影响。另外拓扑统计距离法利用了状态估计及其协方差的信息，性能优于拓扑欧式距离法。

表1 各算法单次平均耗时(ms)

图2 航向估计误差

图3 拓扑统计距离法门限系数比较

图4 拓扑欧式距离法门限系数比较

图5 环境1航迹正确关联率

图6 环境2航迹正确关联率

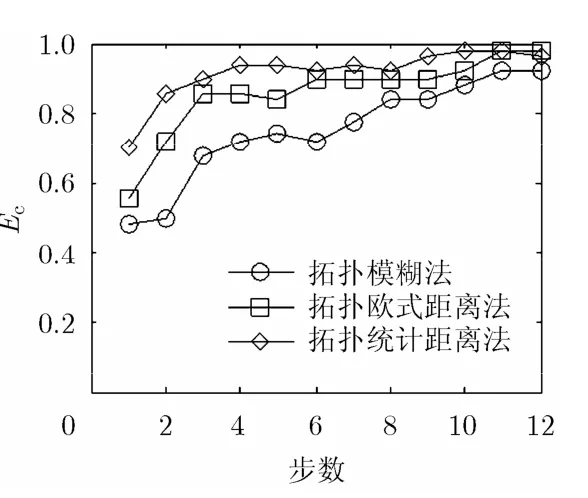
图7 环境3航迹正确关联率

表1为各算法在3种环境下的单次平均耗时。可见拓扑模糊法的实时性最好，拓扑欧式距离法居中，拓扑统计距离法耗时最长。分析各算法计算耗时，除数据转换耗时以外，主要受两部传感器观测航迹数量(分别为n1和n2)影响，因为关联判断需要对所有航迹进行遍历。其中，拓扑模糊法在数据转换后需进行一次遍历判断，计算复杂度约为O( n1×n2)，而拓扑统计距离法和拓扑欧式距离法需要完成双重遍历，计算复杂度约为O(( n1×n2)2)，因此计算量显著增加。此外，拓扑统计距离法与拓扑欧式距离法相比，需要同时转换状态估计及其协方差，计算量更大。可见，拓扑统计距离法的性能总体最好，不足是耗时较大，在实际应用中，可以根据系统误差无关信息量，设置如速率，航向变化率等粗关联门限剔除不必要的参照目标关联对，可大幅降低关联判断次数，减少耗时。

5 结论

为充分利用航迹拓扑信息并考虑传感器虚警和漏报对拓扑结构的影响，本文提出一种基于拓扑统计距离的航迹抗差关联算法，该算法充分利用了传感器观测航迹的状态估计及其协方差信息，提高拓扑目标关联的准确性，同时根据拓扑目标关联结果建立参照目标之间的关联度，在双门限准则下完成参照目标关联判决。仿真结果验证了采用本文算法的有效性，能够为系统误差配准提供可靠的航迹关联对。由于算法要求对各传感器目标进行双重遍历判断，耗时较大，可以根据系统误差无关信息量，如速率，航向变化率等进行粗关联筛选参照目标关联对，减少不必要的数据转换和关联判断，提高算法效率。

[1] Mori Shozo, Chang Kuo-chu, and Chong Chee-yee. Comparison of track fusion rules and track association metrics[C]. 15th International Conference on Information Fusion, Singapore, 2012: 1996-2003.

[2] Bahador K, Khamis A, Karray F O, et al.. Multisensor data fusion: a review of the state-of-the-art[J]. Information Fusion, 2013, 14(1): 28-44.

[3] 郭蕴华, 袁成. 一种异步航迹关联的变异蚁群算法[J]. 电子学报, 2012, 40(11): 2200-2205. Guo Yun-hua and Yuan Cheng. A mutation ant colony algorithm for the asynchronous track correlation[J]. Acta Electronica Sinica, 2012, 40(11): 2200-2205.

[4] 石玥, 王钺, 王树刚, 等. 基于目标参照拓扑的模糊航迹关联方法[J]. 国防科技大学学报, 2006, 28(4): 105-109. Shi Yue, Wang Yue, Wang Shu-gang, et al.. Fuzzy data association based on target topology of reference[J]. Journal of National University of Defense Technology, 2006, 28(4): 105-109.

[5] 杨哲, 韩崇昭, 李晨, 等. 基于目标之间拓扑信息的数据关联方法[J]. 系统仿真学报, 2008, 20(9): 2357-2360. Yang Zhe, Han Chong-zhao, Li Chen, et al.. Data association based on target topology[J]. Journal of System Simulation, 2008, 20(9): 2357-2360.

[6] 方亮. 系统偏差条件下的航迹相关技术研究[D]. [硕士论文],国防科学技术大学, 2009. Fang Liang. Research on track correlation with system bias[D]. [Master dissertation], National University of Defense Technology, 2009.

[7] 曾昊, 王壮. 基于编队结构特征的海面舰船目标关联方法[J].火力与指挥控制, 2012, 37(4): 90-93. Zeng Hao and Wang Zhuang. A vessel targets association algorithm based on the structure of the vessels formation[J]. Fire Control & Command Control, 2012, 37(4): 90-93.

[8] 吴泽民, 任姝婕, 刘熹. 基于拓扑序列法的航迹关联算法[J].航空学报, 2009, 30(10): 1937-1942. Wu Ze-min, Ren Shu-jie, and Liu Xi. Topology sequence based track correlation algorithm [J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(10): 1937-1942.

[9] 吴泽民, 邱正伦, 任姝婕. 多传感器航迹相关的区域匹配算法[J]. 弹箭与制导学报, 2011, 31(4): 210-213. Wu Ze-min, Qiu Zheng-lun, and Ren Shu-jie. Area matching algorithm for multi-sensor track correlation[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2011, 31(4): 210-213.

[10] 宋强, 熊伟, 马强. 基于目标不变信息量的模糊航迹对准关联算法[J]. 系统工程与电子技术, 2011, 33(1): 190-195. Song Qiang, Xiong Wei, and Ma Qiang. Fuzzy track alignment-correlation algorithm based on target invariable information [J]. Systems Engineering and Electronics, 2011, 33(1): 190-195.

[11] Liu Xi, Yin Hao, Tian Chang, et al.. An improved 2-d assignment algorithm for track-to-track association[C]. Control and Decision Conference, Guiyang, 2013: 3698-3703. [12] Kragel B, Herman S, and Roseveare N. A comparison of methods for estimating track-to-track assignment probabilities[J]. IEEE Transactions on Aerospace and Electronic System, 2012, 48(3): 1870-1888.

[13] 盛卫东, 林两魁, 安玮, 等. 基于全局最优的被动多传感器多目标轨迹关联算法[J]. 电子与信息学报, 2010, 32(7): 1621-1625. Sheng Wei-dong, Lin Liang-kui, An Wei, et al.. A passive multisensor multitarget track association algorithm based on global optimization[J]. Journal of Electronics & Information Technology, 2010, 32(7): 1621-1625.

[14] 何友, 王国宏, , 等. 多传感器信息融合及应用[M].(第2版), 北京: 电子工业出版社, 2007: 145-149. He You, Wang Guo-hong, Lu Da-jin, et al.. Multisensor Information Fusion with Applications[M]. (Second Edition). Beijing: Publishing House of Electronics Industry, 2007: 145-149.

董 凯： 男，1986年生，博士生，研究方向为目标跟踪、航迹关联、系统仿真.

王海鹏： 男，1985年生，讲师，研究方向为多传感器多目标跟踪.

刘 瑜： 男，1986年生，博士生，研究方向为分布式传感器网络、多目标状态估计.

Anti-bias Track Association Algorithm Based on Topology Statistical Distance

Dong Kai Wang Hai-peng Liu Yu
(Research Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai 264001, China)

The topology information of the targets observed by sensors can be used to solve the track association problem under the condition of systematic bias. However, the traditional algorithms don’t make full use of track information and are not fit for the presence of sensor’s false alarm and missing detect. An anti-bias track association algorithm based on topology statistical distance is proposed. First, the target state estimation and covariance is converted to acquire the topology description in the coordinates of the reference target. Then the global optimization association is realized based on the derivation of topology statistical distance. Finally, the average statistic distance of neighboring target association pairs in the coordinates of the reference target is applied as the association degree of the reference targets, and the reference target’s association judgment is accomplished according to the double threshold rule. The simulation results show that the performance of the proposed algorithm is apparently better than the traditional algorithm under the conditions of dense formation, random distributed targets and the presence of sensor’s false alarm and missing detection.

Track association; Systematic bias; Topology statistical distance; Anti-bias

TN957

A

1009-5896(2015)01-0050-06

10.11999/JEIT140244

2014-02-24收到，2014-06-27改回

国家自然科学基金(61032001)和山东省自然科学基金(ZR2012FQ004)资助课题

*通信作者：董凯 188dongkai@163.com