基于幅度调制的连续微波雷达测距研究

郑大青 陈伟民陈 丽 李存龙 章 鹏

(重庆大学光电技术及系统教育部重点实验室 重庆 400044)

基于幅度调制的连续微波雷达测距研究

郑大青 陈伟民*陈 丽 李存龙 章 鹏

(重庆大学光电技术及系统教育部重点实验室 重庆 400044)

为实现实时快速的全天候、高精度、大范围测距，该文提出了基于幅度调制的微波雷达测距方法。在分析主要微波雷达特点的基础上，深入探讨了该方法测尺频率和测距范围、精度之间的数学关系，并利用调制在高频载波的低频信号满足大范围测距需求，采用基于测时技术的高精度测相方法实现高精度与高速度测距，并基于混频器、测时芯片TDC-GP2等器件搭建了雷达实验系统。实验表明，基于TDC-GP2测相单元的测相精度达(2.71×10-4)°，并在2.4 GHz载波、150 kHz调制信号的条件下，对3.0～4.1 m内目标的测距实验证明了系统具有1000 m大范围测距的可行性，且目标处于3.0 m时测距精度为0.0187 m，系统单次平均测距时间为0.02～0.03 s。

微波雷达；测距；测相；测时技术；幅度调制

1 引言

为获取被测目标的距离、位置等信息或确保目标工作状态的安全，在工业制造、大地大气探测、结构健康监测等领域，常常需要对被测目标进行长时间、实时快速的全天候、高精度(毫米级)、大范围(上千米)的距离、位置状态测量[1]，如目标为建造中的大型船舶及飞机、振动中的桥梁和高楼等。为适应它们所处的野外环境，在分析多种无线传感方法后发现，微波因能不受雨雾雪等阻挡，传播衰减小，并能在高温高湿、多灰尘等恶劣环境下全天候工作[2]，使得微波雷达相比激光、超声波等雷达在上述领域更具发展潜力。

按照发射信号形式，微波雷达主要分为脉冲雷达和连续波雷达两大类[3]，其中脉冲雷达主要通过测量发射和接收脉冲的时间差Δt测距，其测距精度由测时精度δ( Δt)决定(R为距离，c为光速)，即δR=1 mm所需的δ( Δt)=6.67 ps，该测时精度实现难度较大，成本昂贵[3]；此外，回波脉冲在传播过程的失真会使其信号边沿难以准确识别，使得目前脉冲雷达的测量精度一般为数厘米至分米级[3]，无法满足前述毫米级测量。另一类连续波雷达可分为调制型和非调制型雷达[3]，报道的调制型雷达主要为调频连续波雷达[2,3]，其主要利用发射、回波信号间频率差进行测距，以锯齿波调频雷达测距精度δR=c/2B (c为光速)[2]为例，δR=1 mm需要的调频带宽为B=150 GHz，该范围带宽频率实现难度较大，成本非常昂贵，因此目前调频连续雷达测距精度一般为数厘米至分米级，也难满足毫米级测量。另外，非调制型微波雷达包括单频和多频连续雷达，它们通过测量发射、回波信号间相位差φR实现测量，其测距精度测相精度δ( φR)和发射频率f共同决定，由于微波频率f较高，故测距精度δR即使在一般测相精度δ( φR)下也较容易达到毫米级。然而，由于发射天线尺寸L与发射微波波长λ(λ=c/f )相当且成正比(L约为1/4～1/2波长λ)，因此，单频连续雷达测距范围仅为Rm=λ/2，难实现前述大范围(上千米)测量，为此，众多学者提出双频比相法、参差多频法等多频连续雷达突破该限制以同时实现高精度、大范围测距[4,5]。

然而，这些多频雷达方法仍存在不足：双频比相法存在扩大测距范围和提高精度的矛盾；参差多频法需要发射多组双频信号，搜索算法运算量大、系统复杂；多频到双频法对测距精度要求较苛刻；二次相法也需要发射频点较多等[4,5]。总之，多频雷达必须发射多个频率信号(称“测尺信号”)，并按一定算法搜索频点才能同时实现高精度、大范围测距。然而，多频测尺切换会降低测量实时性，并引入测尺切换的机械与电气抖动引起的测量误差[4,5]，且切换速度(数秒级)慢于目标状态变化(如振动桥梁、高楼等)[1]。

综上分析，目前主要微波雷达方法在同时满足实时、全天候、高精度和大范围测量需求时均存在不足，为此，本文提出了基于幅度调制的连续微波雷达方法，并对其进行了理论分析和实验探索。

2 基于调幅连续微波雷达测距原理及分析

在上述分析中，多频连续微波雷达最接近前述领域的测量需求，只在实时测量方面受限，它是由多频测尺切换耗时及其测量误差所致。因此，想要突破该限制、达到实时性测量，就必须避免多测尺切换过程，即只能采用“单频测尺”测距。然而，若直接发射频率f的非调制“单频测尺”的微波测距，其测距范围仅为Rm=λ/2(λ=c/f,c为光速)，由微波频率(吉赫兹)与天线尺寸关系得该范围一般为数厘米至数分米，难以大范围测距。因此，突破实时性限制、满足大范围测距的关键又转换为如何在“单频测尺”条件下扩大测距范围Rm。由Rm=λ/2=c/2f(c为光速)知，扩大Rm就必须降低“单频测尺”频率f，以大多数常规测距要求Rm=1000 m为例，其对应测尺频率为f=150 kHz，而如果测距范围要求大于Rm=1000 m，测尺频率f将低于150 kHz。可知，该频段信号已不属于微波范围，其与微波信号在全天候测量等方面将存在差异，如果直接将其发射，那么天线尺寸将较大，降低了天线安装、测量便利性，甚至无法使用。

如此，要想突破实时测量限制，就必须跳出上述主要微波雷达方法的局限，即需要考虑采用新的方法或技术。为此，分析大量文献后发现，相位式激光测距仪的中低频调制信号(测尺)的测距原理[6,7]可以从理论上有效地突破上述限制，即能满足“单频测尺”条件下扩大测距范围Rm的需求。因此，文章考虑将其“调制激光光强测距”原理借鉴到微波雷达中，即利用“低频测尺”信号调制高频微波载波进行测距，并提出如2.1节的调幅连续微波雷达方法。尽管由通信技术知“调幅信号”容易受噪声等干扰，也可能会包含非线性谐波信号，但由于“调幅微波雷达方法”具有能够实现前述测量领域实时、全天候、高精度、大范围测量需求的巨大潜力，故本文对其进行了理论分析和实验探索，详细分析请见下文。

2.1 基于调幅连续微波雷达测距原理

由上述分析并借鉴“相位式激光测距的中低频信号调制原理”，提出如图1所示的调幅连续微波雷达。图1的中频信号源输出两路相同正弦信号s0( t)，一路用作相位测量参考，另一路用于调制载波sc( t)幅度，调幅后经过功放、发射天线得到发射微波信号st( t),st( t)发射后遇到距离R处目标，目标将其反射回接收天线，得到回波信号sr( t),sr( t)经过低噪声放大后与载波信号sc( t)混频、低通滤波，即同步解调后得到调制信号s0( t)的时延信号sφ(t)，对s0( t)与sφ(t )测相得到相位延迟φR，进一步可求得待测距离R。

2.2 实现实时全天候的大范围测距理论分析

假若图1的中频信号s0( t)是频率、幅度和初相分别为f0,A0及φ0的正弦信号，载波信号sc( t)为频率、幅度和初相分别为fc,Ac及φc的正弦信号，则s0( t)和sc( t)分别表示为

图1 基于调幅连续微波雷达测距原理

假设功率放大器增益为GPA，则得到发射信号将式(1)，式(2)代入得

可见，载波信号sc( t)的幅度被正弦信号s0( t)调制，即按s0( t)规律变化。若发射信号st( t)在发射/接收天线和目标间往返传播时间为Δt(Δt= 2R/c)，则得到接收信号sr( t)为

式中α为发射信号st( t)传播衰减系数。若低噪声放大器增益为GLNA，则整理得到混频后信号src(t)为

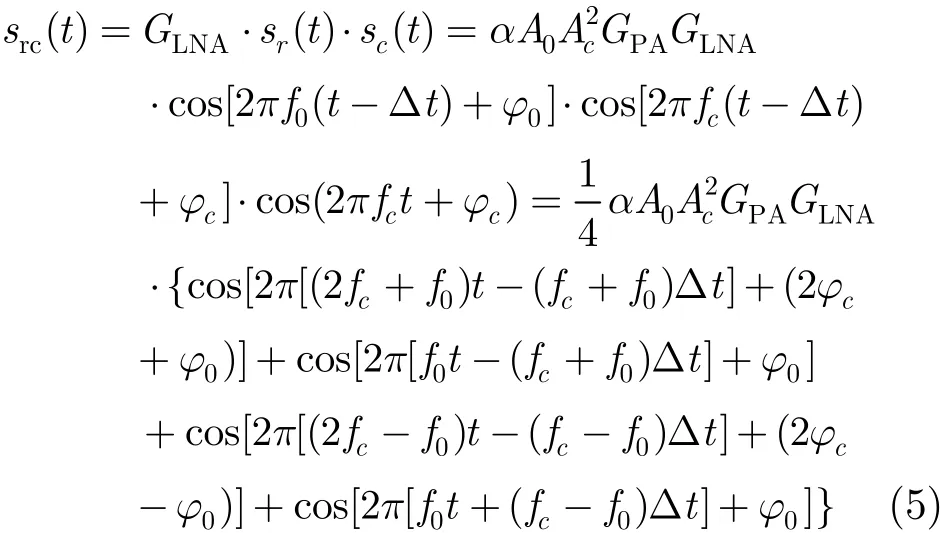
可见，信号src(t)包含4项信号，第1, 3项频率分别为(2fc+f0),(2fc-f0)，第2, 4项频率均为f0，将式(5)信号src(t)通过低通滤波器，得到第2, 4项两项低频f0信号的合成信号sφ(t)为

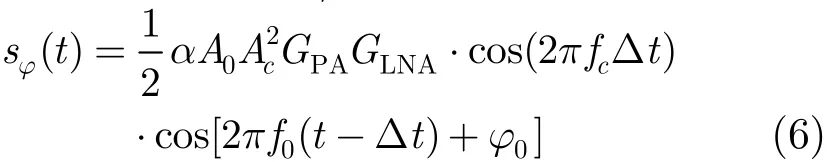
由式(6)知，对固定距离R和雷达发射状态下，信号衰减系数α，延时Δt(Δt=2R /c)，幅度A0, Ac及增益GPA,GLNA均为常数，若设Aφ=则A也为常数，则

φ式(6)为

对比式(1)和式(7)，并利用相位测量单元求得s0( t)与sφ(t)间相位差φR得

将Δt=2R /c代入式(8)，并考虑到相差φR最大可测值为2π，则可得待测距离R及最大测距范围Rm：

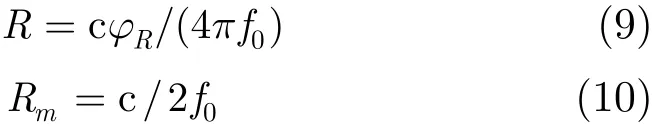
可见，测距范围Rm由中频调制信号s0( t)频率f0决定，即s0( t)即为测尺信号[6,7]。此时，发射天线尺寸L主要限制载波信号sc( t)频率fc的选择范围，而调制信号s0( t)频率f0可降低至数千赫兹或更低、也可高至数十兆赫兹，故式(10)测距范围Rm可达数千米或更远距离。因此，从理论可知基于调幅连续微波雷达具有实现大范围测距的可行性；因“单频测尺信号”s0( t)调制在微波载波sc( t)上，故该雷达还具有实时、全天候测量特点。因此，要想进一步满足前述测量领域高精度测距，还需对其测距精度及其实现方法考察。

2.3 满足高精度测距的测相要求分析

为分析调幅型微波雷达测距精度，假定调制信号s0( t)的频率f0稳定，对式(9)两边微分得

显然，调制信号频率f0越大，测相精度δφR越高(值越小)，测距精度δR越高(值越小)。然而，为了保证式(10)较大测距范围Rm=c/2f0，调制频率f0的增大空间受限。因此，为获得高精度δR测距，需要高测相精度δφR作保障。以大多数常规测距中应用要求为例：测距范围Rm=1000 m、测距精度δR =1 mm，根据式(10)，式(11)求得满足此两个测距要求所需测相精度为δφR=(3.6×10-4)°；如果测距范围大于1 km或精度优于1 mm，所需测相精度还将高于δφR=(3.6×10-4)°。然而，目前主要测相方法如数字相关法、数字傅里叶变换法、欠采样数字鉴相法等大都直接测量相位，且易受到器件参数如采样频率等因素限制，其测相精度一般为(10-2～10-1)°[6- 8]，难以满足上述高精度测相需求，并且它们进行高精度测相成本较昂贵、实现难度较大。

因此，寻找一种同时满足式(10)，式(11)测距范围和精度要求的高精度相位测量方法及系统，是调幅型微波雷达实现实时快速、全天候的大范围、高精度测距的关键。

3 基于高精度测时技术的相位测量法

为实现高精度测相，考虑到主要测相方法受限的原因，并结合目前众多时间测量技术容易达到的测量精度[9](纳秒级或几十皮秒级)以及周期信号时间与相位关系等因素，利用高精度测时技术间接测量相位应是满足高精度测相需求的有效潜在途径。为此，将用图2基于测时技术的测相单元实现图1的相位测量[10]。

图2 基于测时技术的测相原理

可见，原待测信号s0( t)和sφ(t)间相位差φR准确地保留在两低频信号sr 0(t)和srφ(t )间，由于频率由f0降为(f0-fr)，测量信号时间拉长(相差不变)，测相难度减低、测相精度便于提高；进一步分别将sr 0(t)和srφ(t )整形为方波并测出其时间差Δt，并求得它们间相差φR为

当频率f0, fr稳定时，对式(14)两边微分得到

可知，频差值(f0-fr)越小，测时精度δ( Δt)越高(值越小)，测相精度δφR越高(值越小)。又因当fr→f0时，有(f0-fr)→0，由式(15)知，即使在一般测时精度δ( Δt)下(如几十纳秒)，理论上测相精度δφR可以达到很高(值很小)，因此，通过降低参考频率fr可以很方便地提高测相精度δ( Δt)，且提升空间大、便于实现。此外，由于目前众多测时方法精度δ( Δt)较容易达到纳秒级甚至数十皮秒级，且成本较低，因此，式(15)理论上测相精度δφR很容易达到(10-6～10-5)°，远高于当前主要测相方法测相精度(10-2～10-1)°，可为调幅型微波雷达同时实现快速实时、全天候的大范围、高精度测距奠定基础。

4 实验与分析

4.1 相位测量单元的测相实验

为验证上述相位测量方法有效性，需进行测相实验。因为基于延迟线插入原理的数字TDC (Timeto-Digital Converter)技术及芯片具有高精度(几十皮秒级)、测量快速、便于搭建系统等优点，故决定采用测时芯片TDC-GP2搭建包含图1，图2相位测量单元的测相实验系统(如图3所示)[9,11]。

为减小微波雷达系统其他因素对测相实验的影响，故单独对测相单元实验，即利用主信号源输出两路信号模拟图1中信号s0( t),sφ(t)，并用相位测量单元测相(见图3)。为使测相实验更接近系统测距范围和精度的需求，由于1000 m测距范围下mm级测距精度能满足多数常规测距工程应用，故选择测距范围Rm= 1000 m，测距精度δR=1 mm，由式(10)，式(11)得到所需测相精度δφR=(3.6×10-4)°，测尺频率为f0=150 kHz；又考虑到TDC-GP2芯片典型测时精度δ( Δt)=65 ps，将各值代入式(15)得(f0-fr)=15.39 kHz，考虑到测相便利性，取(f0-fr)=10 kHz，此时式(15)理论测相精度将优于(3.6×10-4)°，对应参考频率fr=140 kHz。

K-means算法即已知数据库包含n个数据样本，给定聚类个数k，对每个数据样本计算其应该属于的类，得到满足方差最小标准的k个聚类。

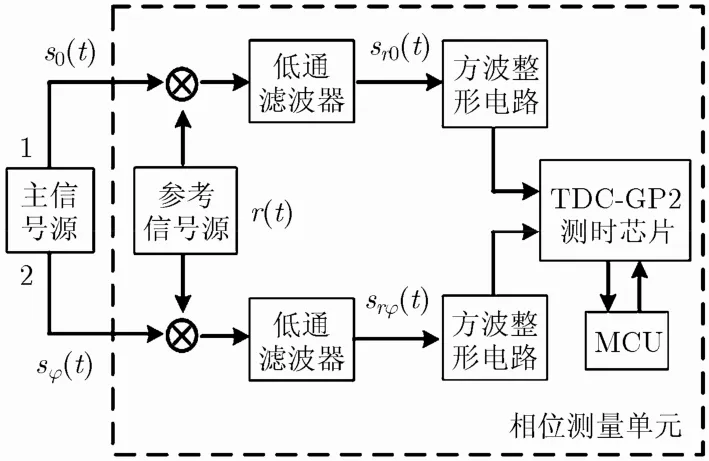
图3 基于高精度测时技术的测相实验系统

图3采用主信号源(RIGOL-DG4102)输出两路频率均为f0=150 kHz的信号s0( t)和sφ(t)，它们间相差φture在用作真实值(0°～180°)；利用参考信号源(AGILENT-33220A)模拟输出频率fr=140 kHz的参考信号r( t)(初相可设任意值)；采用TDC-GP2单元测得两低频方波间时间差Δt，再由式(15)得到相差测量值φmea。为考察系统测相精度，将输出相差固定在φture=20.0°。并对其测量100次，结果如图4，且TDC-GP2测时数据标准差为76.2 ps，与TDC-GP2典型测时精度65 ps基本吻合[9,11]。由图4测相数据得测相精度为(2.71×10-4)°，优于Rm=1000 m, δR=1 mm所需测相精度(3.6×10-4)°。将相差φture固定40°,60°等，测相精度都优于(3.6×10-4)°。因此，测相实验表明上述测相方法及系统可以满足系统大范围、高精度测距的测相需求。

4.2 基于调幅微波雷达的测距实验

图4 相位差为20度时的测相数据

在上述测相实验基础上，为进一步考察雷达测距性能，需搭建测距实验系统：根据前述测尺频率、测相单元参数等选择方法，并考虑实验便利性及系统成本，载波sc( t)频率选为fc=2.4 GHz，因2.4 GHz 是ISM频段标准频点，与之相关器件如混频器、功放等成熟市场化，且选择多、成本低廉。其他重要参数选为：发射信号st( t)功率为30 dBm，。发射、接收天线增益均为14 dB，半波瓣角为15。搭建雷达系统如图5所示。

图5 基于调幅连续微波雷达实验系统

在图5中，雷达系统稳固在参考点上，为增强反射信号，使实验效果明显，被测目标选为一块对微波信号反射性能较好的矩形铝板(600 mm×600 mm×2 mm)，并将铝板与收发天线正对，铝板固定在精密导轨(7STA02600)移动平台上，平台由电机(7SC306)控制，步进距离及时间等均可软件设置，步进距离精度达0.01 mm。

首先考察雷达系统的测距范围性能：由于目标为无源铝板，为便于实验，距离不能取太大，可选取初始距离R= 3.0 m，并设定移动平台的步进距离ΔR =0.1 m，步进时间为20 s，利用系统对每个位置测点测量100次，得到平均数据及其拟合曲线如图6所示，可见设定值X 与测量值Y 线性拟合方程为Y =1.0032X - 0.0024，相关系数0.999。由于图6测距数据由测距式(9)R=cφR/(4πf0)得到，因此，上述测距实验表明，雷达系统测尺频率为f0，即f0=150 kHz，对应最大测距范围由式(10)Rm= c/2f0得到Rm=1000 m。此外，图6中目标位置由3.0～4.1 m的变化量为1.1 m并可测，故从另一角度证明图1调幅型微波雷达突破了同频段微波雷达，即2.4 GHz单频雷达测距范围0.0625 m(2.4 GHz信号的半波长)的限制，具有大范围测距性能。

将文中雷达与其他主要微波雷达的典型参数对比如表1，可见，即使在有噪声干扰等影响下，调幅雷达的测距精度仍不差于脉冲雷达、调频连续雷达，且测距范围、速度分别优于单频、多频连续雷达，具有20～30 ms的单次测量时间能满足桥梁、高楼等动态目标的快速测距要求。

文中被测目标为光滑铝板，但实际应用中微波波束照射的桥面、地面等目标面可能粗糙不平，并将直接影响微波反射、散射系数及其反射、散射功率。此外，微波反射、散射系数还是微波频率、极化方式等因素的复杂函数[12]，而微波反射信号又是由位于与雷达距离相等的目标面上位置点决定、散射信号由处于与雷达不同距离的目标面上位置点决定[12]，因此，目标面粗糙不平对测距及其精度影响也较为复杂。然而，即使目标是粗糙桥面、波动水面，文献[13～15]各微波雷达精度均优于毫米级，说明目标粗糙不平对测距精度影响在可控、可接受范围内。另外，若目标面粗糙度过大，可在目标处安装光滑金属反射器[15]。

图6 调幅微波雷达的多测点测距数据及拟合曲线

图7 调幅微波雷达单测点多次测距数据

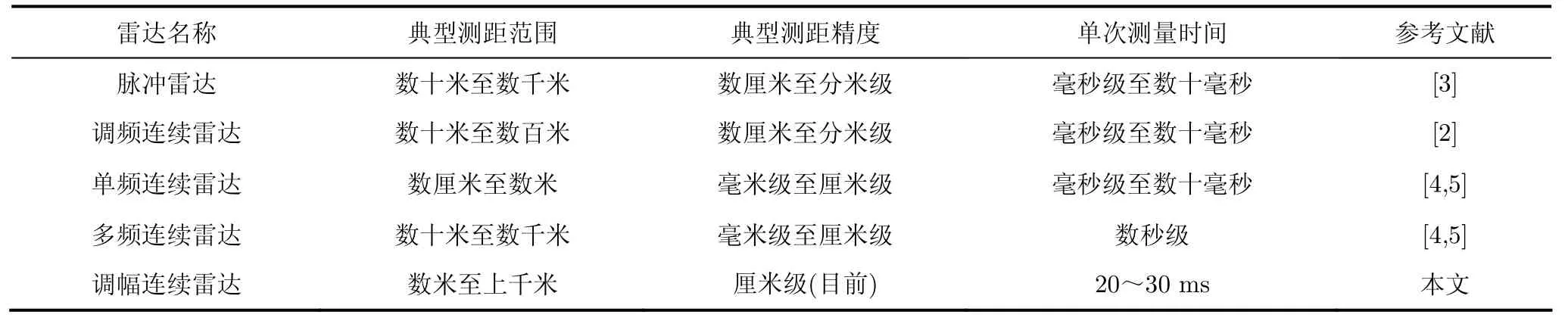
雷达名称 典型测距范围 典型测距精度 单次测量时间 参考文献脉冲雷达 数十米至数千米 数厘米至分米级 毫秒级至数十毫秒[3]调频连续雷达 数十米至数百米 数厘米至分米级 毫秒级至数十毫秒[2]单频连续雷达 数厘米至数米 毫米级至厘米级 毫秒级至数十毫秒[4,5]多频连续雷达 数十米至数千米 毫米级至厘米级 数秒级[4,5]调幅连续雷达 数米至上千米 厘米级(目前) 20～30 ms 本文

综上，基于调幅微波雷达方法及系统，在满足全天候条件下可达到1000 m大范围测距要求、具有毫米级高精度测距潜力，并且单次测距平均耗时仅为0.02～0.03 s，系统更高精度测距(毫米级)实验将后续开展。

5 结论

理论分析证明，基于幅度调制的连续微波雷达与基于高精度测时的测相方法结合，确实能突破目前主要微波雷达应用限制，并满足实时快速的高精度、大范围测距的需求。测相实验表明，基于TDCGP2芯片测相单元的测相精度达到(2.71×10-4)°，比常规相位测量精度提高约2～3个数量级，满足大范围、高精度微波测距的理论测相要求；进一步测距实验表明，在载波频率为2.4 GHz、测尺频率为150 kHz情况下，雷达实验系统对3.0～4.1 m范围内目标的测距实验验证了系统最大测距范围为1000 m，即突破了同频段2.4 GHz单频微波雷达测距范围(0.0625 m)限制，并且系统在R=3.0 m的测距精度为0.018 7m，为实现全天候条件下大范围(1000 m)、高精度(mm级)微波雷达测距奠定了基础，且实验系统单次平均耗时为0.02～0.03 s，实时快速。

[1] 贾方秀, 丁振良, 袁峰, 等. 基于全相位快速傅里叶变换谱分析的激光动态目标实时测距系统[J]. 光学学报, 2010, 30(10): 2928-2934. Jia Fang-xiu, Ding Zhen-liang, Yuan Feng, et al.. Real-time laser range finding system for moving target based on all-phase fourier transform spectrum analysis[J]. Acta Optica Sinica, 2010, 30(10): 2928-2934.

[2] 周洪, 邹祥林, 吴邦春. FMCW雷达港口起重机防撞系统的设计与开发[J]. 仪器仪表学报, 2007, 28(9): 1689-1694. Zhou Hong, Zou Xiang-lin, and Wu Bang-chun. Design and development of port crane crash-preventing system based on FMCW radar[J]. Chinese Journal of Scientific Instrument, 2007, 28(9): 1689-1694.

[3] 袁其平, 范立洁, 童峥嵘, 等. 脉冲雷达测距时间-电压转换方法[J]. 现代雷达, 2012, 34(6): 69-73. Yuan Qi-ping, Fan Li-jie, Tong Zheng-rong, et al.. A study on time-voltage conversion method for pulse radar ranging[J]. Modern Radar, 2012, 34(6): 69-73.

[4] 曹延伟, 江志红. 加速运动目标的双频比相测距算法研究[J].电子与信息学报, 2007, 29(12): 2858-2862. Cao Yan-wei and Jiang Zhi-hong. Research on algorithm of dual frequency ranging for target with acceleration [J]. Journal of Electronics & Information Technology, 2007, 29(12): 2858-2862.

[5] 曹延伟, 程翥, 皇甫堪, 等. 多频连续波雷达两种测距算法研究[J]. 电子与信息学报, 2005, 27(5): 789-792. Cao Yan-wei, Cheng Zhu, Huangfu Kan, et al.. The research on two algorithms for multiple frenquency CW radar ranging[J]. Journal of Electronics & Information Technology, 2005, 27(5): 789-792.

[6] 廖平, 蔡玉鑫. 改进型相位式激光测距电路的设计[J]. 激光与红外, 2013, 43(4): 356-359. Liao Ping and Cai Yu-xin. Improved design of phase laser range finder circuit[J]. Laser & Infrared, 2013, 43(4): 356-359.

[7] 缑宁祎, 张珂殊. 高速相位式激光测距数字鉴相方法仿真与实现[J]. 红外与激光工程, 2012, 41(9): 2358-2363. Gou Ning-yi and Zhang Ke-shu. High speed digital phase difference measuring methods simulation and implementation in phase-shift laser range finder[J]. Infrared and Laser Engineering, 2012, 41(9): 2358-2363.

[8] 王心遥, 张珂殊. 基于欠采样的激光测距数字鉴相方法[J]. 红外与激光工程, 2013, 42(5): 1330-1337. Wang Xin-yao and Zhang Ke-shu. Digital phase-shiftmeasuring methods based on sub-sampling in laser range finder[J]. Infrared and Laser Engineering, 2013, 42(5): 1330-1337.

[9] 岱钦, 耿岳, 李业秋, 等. 利用TDC-GP21的高精度激光脉冲飞行时间测量技术[J]. 红外与激光工程, 2013, 42(7): 1706-1709. Dai Qin, Geng Yue, Li Ye-qiu, et al.. High-precision measurement technology of laser pulse flight time based on TDC-GP21[J]. Infrared and Laser Engineering, 2013, 42(7): 1706-1709.

[10] Liu S, Tan J, and Hou B. Multicycle synchronous digital phase measurement used to further improve phase-shift laser range finding[J]. Measurement Science and Technology, 2007, 18(6): 1756-1762.

[11] 张黎明, 张毅, 赵欣, 等. 基于TDC的激光测距传感器飞行时间测量研究[J]. 传感器与微系统, 2011, 30(12): 71-74. Zhang Li-ming, Zhang Yi, Zhao Xin, et al.. Study on flight time measurement laser ranging sensor based on TDC[J]. Transducer and Microsystem Technologies, 2011, 30(12): 71-74.

[12] 段锐, 张海, 陈祝明, 等. 垂直入射区雷达地面散射系数测量与特性研究[J]. 电子科技大学学报, 2012, 41(3): 373-377. Duan Rui, Zhang Hai, Chen Zhu-ming, et al.. Radar terrain scattering return measurement and characteristics research in vertical incidence region[J]. Journal of University of Electronic Science and Technology of China, 2012, 41(3): 373-377.

[13] Grazzini G, et al.. Simple microwave sensor for remote detection of structural vibration[J]. Electronics Letters, 2009, 45(11): 567-569.

[14] Kim S and Nguyen C. A displacement measurement technique using millimeter-wave interferometry[J]. IEEE Transactions on Microwave Theory and Techniques, 2003, 51(6): 1724-1728.

[15] Wang G, Gu C, Rice J, et al.. Highly accurate noncontact water level monitoring using continuous-wave Doppler radar[C]. 2013 IEEE Topical Conference on Wireless Sensors and Sensor Networks (WiSNet), San Diego, California, USA, 2013: 19-21.

郑大青： 男，1985年生，博士生，研究方向为传感测量技术、智能结构健康状态监测等.

陈伟民： 男，1955年生，教授，博士生导师，研究方向为光电技术及系统、传感器技术、智能结构健康状态监测等.

Investigation on Ranging of the Continuous Microwave Radar Based on Amplitude Modulation

Zheng Da-qing Chen Wei-min Chen Li Li Cun-long Zhang Peng
(Key Laboratory of Optoelectronic Technology and System of Ministry of Education, Chongqing University, Chongqing 400044, China)

In order to meet the needs of high speed and real-time, all-weather, high-precision and large-scale ranging, the method of continuous microwave radar with amplitude modulation is proposed. Based on the analysis of the characteristics of the main microwave radar ranging methods, the mathematical relationships among the modulation frequency, measurement range and its accuracy are deeply discussed in the method, in which the low single frequency signal modulated on high frequency carrier signal is adopted to get large-scale ranging and also the time-measurement technology with high precision is used to achieve high precision and high speed ranging. Finally, the experimental radar system is set up by the mixer and the time-measurement chip TDC-GP2 etc. The experiments of the phase difference measurement unit based on TDC-GP2 show its accuracy isdegrees. When the frequency of carrier signal is 2.4 GHz and that of modulation signal is 150 kHz, the experimental results under the distance from 3.0～4.1 m verify the effectiveness that the radar system could achieve large-scale ranging of 1000 m, and show that the ranging accuracy is 0.0187 m of distance of 3.0 m. Moreover, the average ranging time for single measuring point is about 0.02～0.03 s.

Microwave radar; Ranging; Phase measurement; Time measurement technology; Amplitude modulation

TN958

A

1009-5896(2015)01-0043-07

10.11999/JEIT140238

2014-02-24收到，2014-07-14改回

国家自然科学基金(51078369)和中央高校基本科研业务费科研专项项目(CDJXS10120002)资助课题

*通信作者：陈伟民 wmchen0802@126.com