带有积分型边值条件的奇异的n阶边值问题无穷多正解的存在性

武 晨

（江苏联合职业技术学院南京分院，江苏 南京 210019）

0 引言

近年来，带有积分型边值条件的边值问题在热传导、半导体以及流体力学等领域有着越来越重要的应用（见［1-2］），并且随着研究的深入也取得了一系列重要成果（见［3-7］）.文献［7］研究了一个二阶奇异的带有积分型边值条件的边值问题：，作者通过利用复合单调算子理论证明了上述边值问题的解是存在唯一的.文献［8］考虑了如下的一个奇异的n阶m点边值问题：，应用不动点指数理论证明了其正解的存在性.我们知道积分型边值条件包含了多点边值这一特殊情况，事实上，如果我，其中k≥1 是一个正整数，ai,bi∈[0,+∞)是一个(0,1)中的有限点列，χ(s)是[0,+∞)上的特征函数，即：则边值条件（2）就退化为：

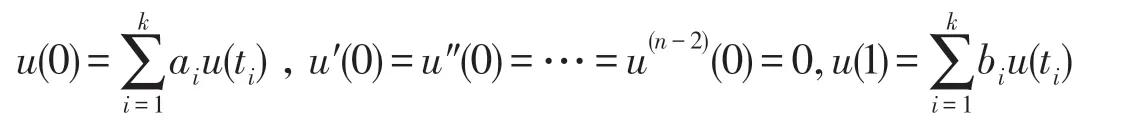
受以上文献的启发，笔者研究在(0,1)区间上一个带有积分型边值条件的奇异的n阶边值问题：

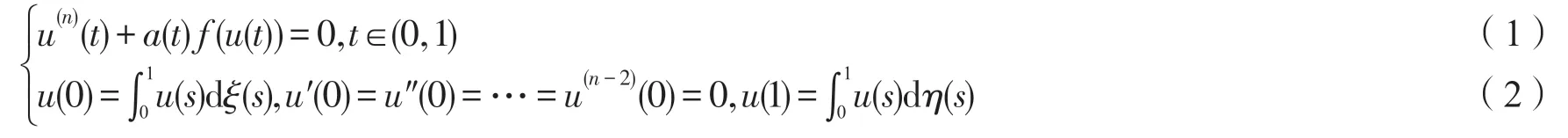
无穷多正解的存在性.其中，n≥2,ξ(s),η(s)非减，a(t)∈Lp[0,1](p≥1)，并且a(t)在中有可数多个奇异点，边值条件中的积分是Riemann-Stieltjes 型积分，边值问题（1）（2）的正解是指存在函数u∈C1[0,1]⋂Cn(0,1)，使得当t∈(0,1)时有u(t)＞0 成立，且满足（1）（2）.

在本文中，我们假设以下条件成立：

H1：存在序列

H2：存在H＞ 0，使得当t∈[t*,1-t*]时有a(t)≥H成立；

H3：存在p≥1，使得a(t)∈Lp[0,1]；

H4：f∈C([0,+∞),[0,+∞))；

另外，由ξ(s),η(s)非减可知，

1 一些引理和定义

引理1设E是一个Banach空间，P是E中的锥，假设Ω1,Ω2是E中满足的两个开子集，且是一个全连续算子，满足：（i）‖Tu‖≤‖u‖，u∈P⋂∂Ω1，且‖Tu‖≥‖u‖，u∈P⋂∂Ω2；或者（ii）‖Tu‖≥‖u‖，u∈P⋂∂Ω1，且‖Tu‖≤‖u‖，u∈P⋂∂Ω2；则T在中至少有一个不动点.

引理2［9］

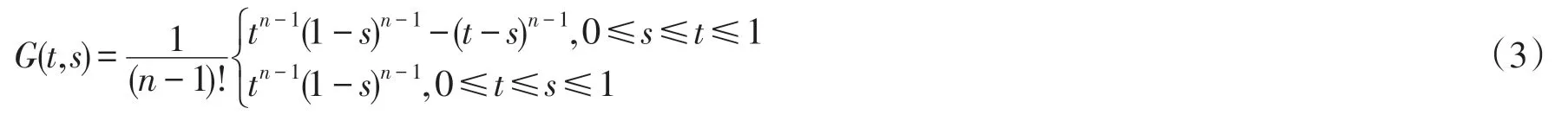
且格林函数G(t,s)满足：

（i）G(t,s)≥0 在 [0,1]×[0,1]上连续；

（ii）G(t,s)≥G(θ1(s),s)(t,s∈(0,1)),∀τ∈，存在常数，使得

观察组护理后收缩压为(141.3±13.1)mm Hg、舒张压为(83.4±7.8)mm Hg、总胆固醇为(5.1±0.7)mmol/L、甘油三酯为(2.7±0.3)mmol/L、纤维蛋白原为(3.2±0.8)g/L;对照组护理后收缩压为(159.7±14.2)mm Hg、舒张压为(94.6±8.4)mm Hg、总胆固醇为(6.7±0.9)mmol/L、甘油三酯为(4.5±0.8)mmol/L、纤维蛋白原为(3.5±0.9)g/L,观察组各项指标改善情况优于对照组(P<0.05)。

其中

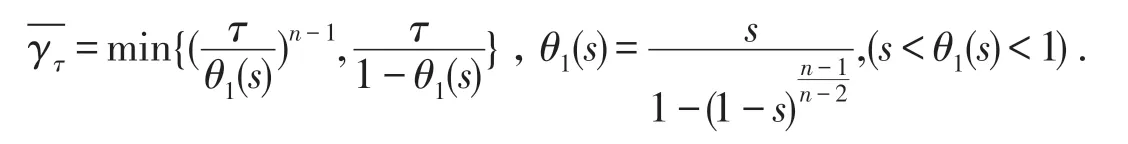
为了方便，我们记G(θ1(s),s)=G1(s).

引理3设g∈L(0,1)，则方程u(n)(t)+g(t)=0,t∈(0,1)对应于边值问题（2）的唯一解为：

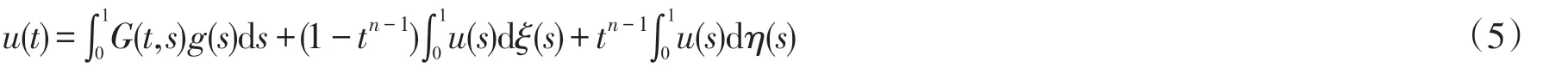
为了应用（4），我们定义一个特殊的锥，设E=C[0,1]，赋予范数则E是一个 Banach 空间，对任意固定的，定义锥：

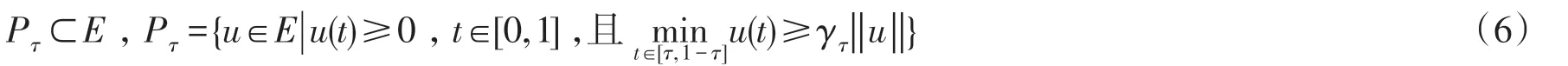
其中

定义算子T:

显然，u(t)是边值问题（1）（2）的解当且仅当u(t)是算子T的不动点.

引理4，算子T:Pτ→Pτ，并且T全连续.

证明由条件显然可知Tu(t)≥0，

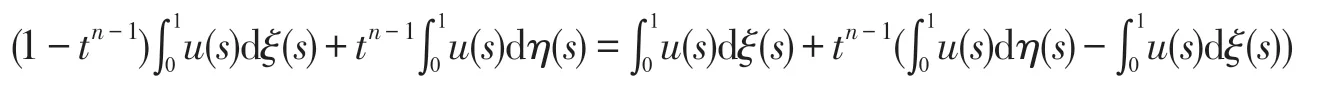
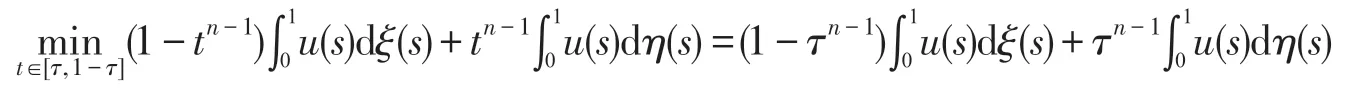
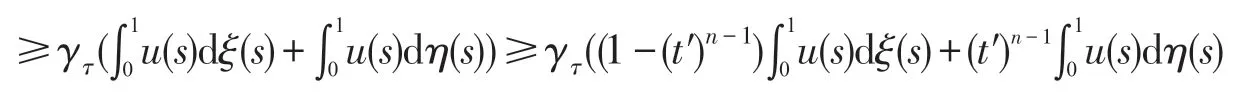
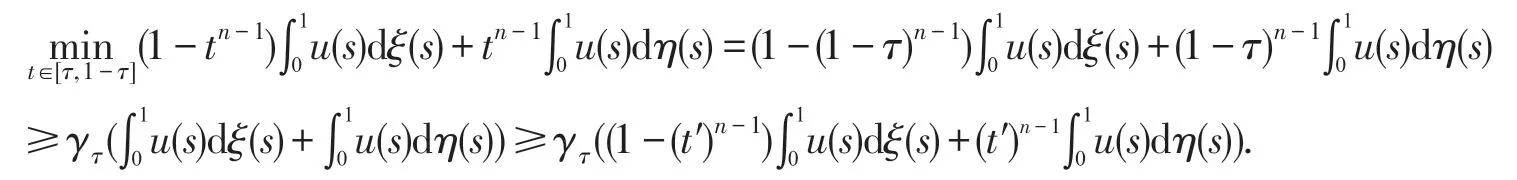
令u∈Pτ，∀t′∈[0,1]，由（4）（7）有：

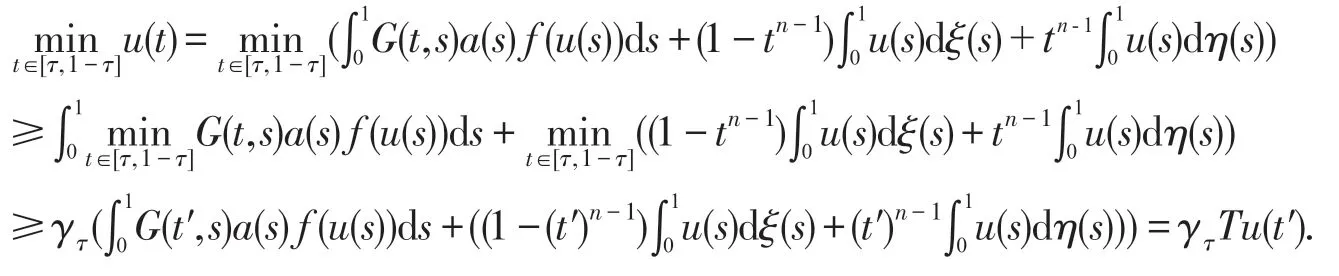
2 主要结论

为了方便，给出以下记号：

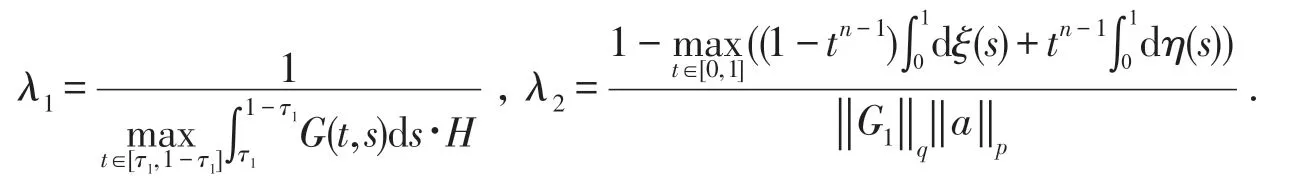
定理1假设(H1)-(H5)成立，设满 足tk+1＜τk＜tk,k=1,2,…, 令满足：Rk+1＜γτkrk＜rk＜Rk，Mrk＜LRk,k=1,2,…，其中M∈(λ1,+∞)，L∈(0 ,λ2)，更进一步，对每个自然数k，假设f满足如下的增长性条件：H6：f(u)≤LRk,u∈[0,Rk]；H7：f(u)≥Mrk,u∈[γτkrk,rk].则，边值问题（1）（2）有无穷多个正解，满足rk≤ ‖uk‖≤Rk,k=1,2,….

证明定义E中的开子集：Ω1,k={u∈E|‖u‖≤Rk}，Ω2,k={u∈E|‖u‖≤rk}如上面假设，令，定义锥，固定k，对任意的u∈Pk⋂∂Ω2,k,s∈[τk,1-τk]，有，由H2、H5和H7可知：

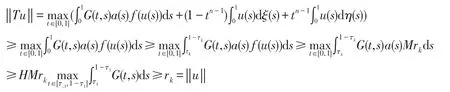
令u∈Pk⋂∂Ω1,k，则u(s)≤‖u‖≤Rk.由H5、H6有：

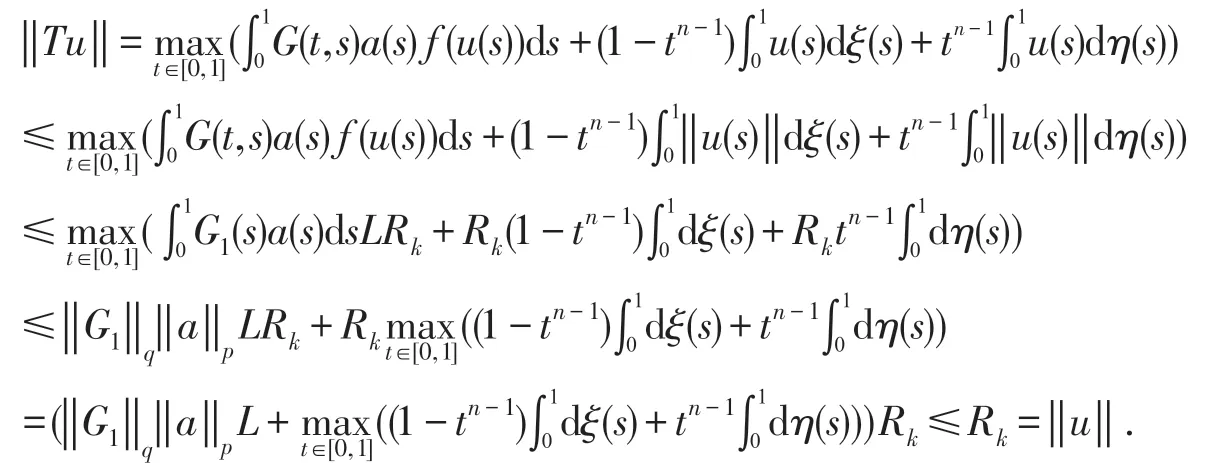
［1］CANNO J R.The solution of heat equation subiect to the specification of energy［J］.Quart Appl Math，1963，21（2）：155-160.

［2］IONKIN N I.Solution of a boundary value problem in heat conduction theory with nonlocal boundary conditions［J］.Dif⁃ferential Equations，1997，13：294-304.

［3］BOUCHERIF A.Second-order boundary value problems with integral boundary conditions［J］.Nonlinear Anal，2009，70：364-371.

［4］GUO Dajun.A boundary value problem fornth order integro-differential equations in a Banach space［J］.Appl Math Com⁃put，2003，136：571-592.

［5］YANG Yang,ZHANG Jihu.Existence of solutions for some discrete boundary value problems with a parameter［J］.Appl Math Comput，2009，211：293-302.

［6］YANG Zhilin.Positive solutions of a second order integral boundary value problem［J］.J Math Anal Appl，2006，321：751-765.

［7］KONG Lingju.Second order singular boundary value problems with integral boundary conditions［J］.Nonlinear Analysis，2010，72：2628-2638.

［8］ZHANG Mingchuan，YIN Yanmin，WEI Zhongli.Positive solutions of singular higher-orderm-point boundary value prob⁃lem with nonlinearity that changes sign［J］.Appl Math Comput，2008，201：678-687.

［9］JI Yude，GUO Yanping.The existence of countably many positive solutions for some nonlinearnth orderm-point boundary value problems［J］.J Comut Appl Math，2009，232：187-200.