分片光滑系统中一类具非初等奇点的擦边闭轨分支

汪 瑞，李 洁，梁 峰

（安徽师范大学 数学与计算机科学学院，安徽 芜湖 241000）

0 引言

分片光滑动力系统在物理学、工程学等学科有着广泛的应用.近年来，人们尝试将用于研究光滑系统的分支方法，如Hopf 分支、同宿环分支、次调和解分支等方法，推广到非光滑系统，见［1-4］.如文［3］将Hopf分支和同宿环分支的一阶Melnikov方法推广到分片光滑系统.文［4］将平均方法也推广应用到分片光滑系统.

一阶Melnikov函数方法在平面光滑近哈密顿系统的极限环分支方面有着广泛的应用，见［5-7］.文［3］将这一方法推广到分片光滑近哈密顿系统中，并给出了一阶Melnikov函数的积分公式.进而，文［8］应用该公式研究了一类具有初等奇点的广义同宿环和双同宿环附近的极限环分支问题.

本文我们研究未扰系统有一擦边闭轨的分片光滑近哈密顿系统的极限环分支.假设该擦边闭轨切y轴于坐标原点，其中y轴为非光滑区域的分界线，原点为这个未扰系统的非初等奇点.假设在这个擦边闭轨附近有一族分片光滑的周期轨.扰动这个分片光滑的哈密顿系统，可能由这族周期轨分支出极限环.在本文中，我们仍使用［3］中给出的公式来研究这类擦边闭轨附近的一阶Melnikov 函数的展开式和擦边闭轨附近分支出极限环的个数，进而推广文［8］的部分结果.

1 主要结果

我们考虑如下形式的分片光滑系统

其中

H±,p±,q±∈C∞在 R2上，ε≥0 且任意小，δ为紧集D⊂R2上的一个向量参数，s为一正整数，从而系统（1）有两个C∞系统，分别称之为右子系统和左子系统

当ε=0 时，对子系统（2）和（3）同文［8］，我们给出如下假设

假设I存在α＞0 使得 (2)ε=0，当H+(x,y)=h,h∈(-α,α)时，有一族顺时针方向周期闭轨.当h=0时，与y轴相切于原点且满足时，令⋂{x=0}={A(h),B(h)}，其中A(h)=(0,a(h)),B(h)=(0,b(h))且b(h)＜0＜a(h),0≤h＜α,A(0)=B(0),见图1a.

假 设II＞0,见图1b.

在假设I和II下，当ε=0 时，系统（1）在擦边闭轨的外侧存在一族周期闭轨，记为Lh，见图1c.由［9］中定义1.4，我们知道，当m≥2 时，原点是系统(1)ε=0的非初等奇点；而当m=1 时，原点是初等奇点，这种情况在［8］中已有研究.本文研究当m≥1 的一般情况，实际上是［8］中的部分结果的更一般化.

图1 系统（1）在假设I和II下的轨迹

因系统(1)ε=0有两族闭轨，其中一族是Lh，位于外侧；另一族位于内侧，记作.相应地，有如下两个Melnikov函数，

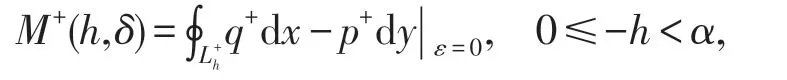
和

上述关于M(h,δ)的公式由［3］给出，其中，

由于（2）是C∞的，所以当 |h|＜α时，函数M+(h,δ)也是C∞的.因此，当 |h|≪1 时，对于任意的整数k≥1，我们有

其中，由［7］知

下面给出本文的主要定理

定理1.1假设I和II都成立，则当0＜h≪1时，一阶Melnikov函数M(h,δ)有如下展开式

定理1.2设（5）式和（6）式成立，且存在l≥0,δ0∈D使得Cj(δ0)=0,j=0,1,…,l,Cl+1(δ0)≠0,以及

则，（1）当l=(m+1)k+n，0≤n＜m,k≥0 时，系统（1）在擦边闭轨附近可分支出极限环.

（2）当l=(m+1)k+m,k≥0 时，系统（1）在擦边闭轨附近可分支出个极限环.

2 主要定理的证明

为了获得M(h,δ)在h=0 附近的展开式，我们首先给出一些引理.易见，（5）式中的系数可用来研究在内侧的极限环分支.为了研究在外侧的极限环分支，我们要知道m(h,δ)在 0＜h≪ 1 上的展开式.在（4）式中，当 0≤h＜α时，令

由［3］和假设I可得

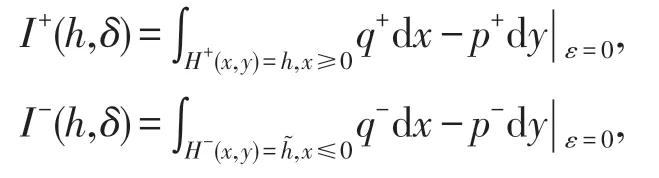
其中h=H-(0,a(h))，0≤h＜α.在假设I和II下，H+和H-在原点附近的展开式可写为

同文［8］的引理2.1和2.2，有如下两个引理成立.

引理2.1当假设I 成立且0＜h≪1 时，方程H+(0,y)=h有两个解其 中是 一 个C∞函 数，且 满 足从 而 有

引理2.2当假设I和II都成立时，有，其中A,B由假设I所定义.

根据引理2.2和（4）式知

令

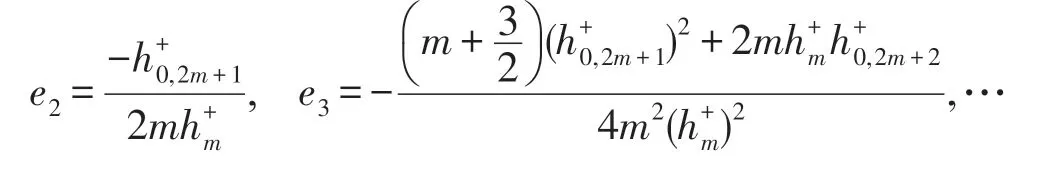
再由假设II和引理2.1得

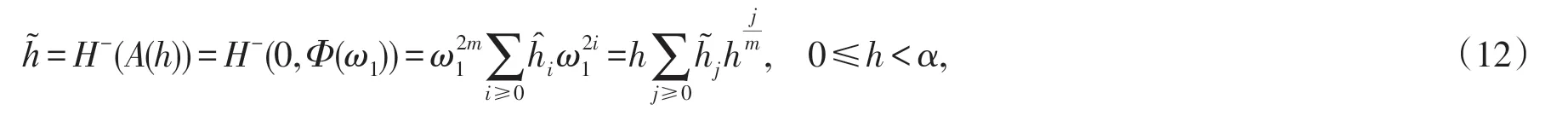
在假设II中，当 ||y充分小时，有

其中

其中

由隐函数定理，易见如下引理成立.

引理2.3当0＜h≪1时，方程H+(x,y)=h在(0,0)点附近关于x有唯一解

其中ω=H*(y)-h，H*(y)=H+(0,y).

当 0＜h≪1时，y轴将分成两部分：，见图1a.因此，

其中，M+(h,δ)由（5）式给出，下面首先给出I+1(h,δ)在 0＜h≪1内的展开式.

其中

且满足

在原点附近，令

其中

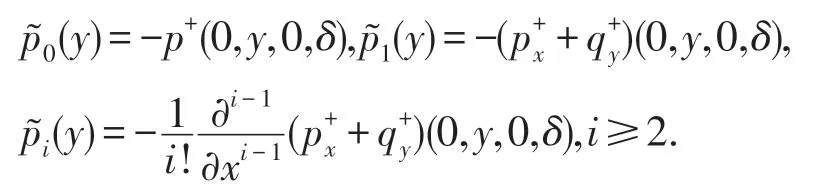
根据引理2.3，可将C∞函数Ψ(y,ω)写为

令

其中

再由引理2.3知，Ψ(y,ω)满足

把（19）式代入上式，我们得到

记

由（17）和（19）可得

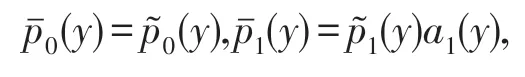
因此，令u=Φ-1(y)（Φ是引理2.1中所定义），由（16）与（21）可得

然后，由（11），（22）和（24）可得

把（24）代入（23）得

其中

引理2.4对任意一对(i,j)，有

其中，当i是偶数时，

引理2.5函数I+1(h,δ)有如下形式的展开式

其中

证明由（26）和引理2.4可得

由引理2.4和2.5知

综合（5），（15）和引理2.5，I+(h,δ)有如下展开式

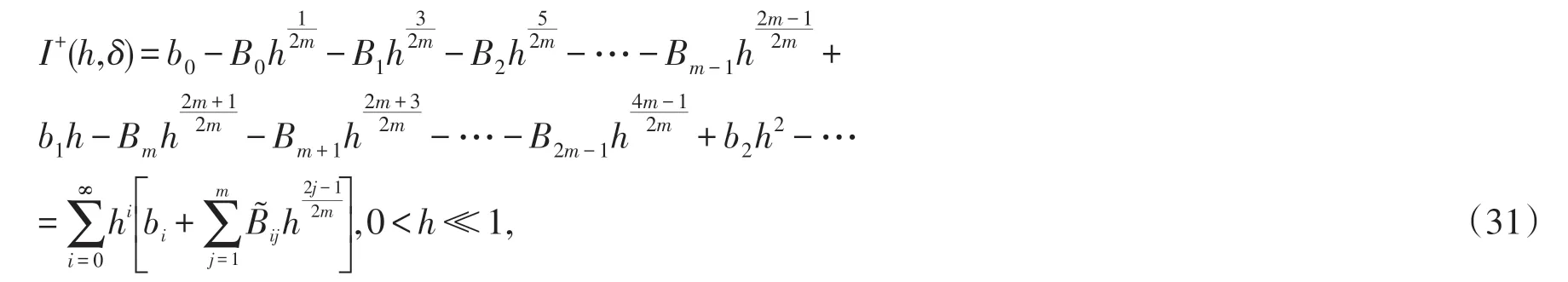
其中Bij=-Bim+j-1.

类似于（29）的推导方法可得

其中

把（12）代入（32）有

定理1.1的证明当 0＜h≪1时，把（14），（31）和（34）代入（10）得

定理1.2的证明不失一般性，设Cl+1(δ0)＞0.

（1）当l=k(m+1)+n,k≥0,0≤n＜m时，根据（7）式，我们可选择C0,C1,C2,…,Cl为自由参数.若l为偶数，取 0＜-C0≪C1≪ -C2≪… ≪Cl-1≪-Cl≪1，由（6）式知，M(h,δ)在h=0 附近有l+1 个正的单根.若l为奇数，取 0＜C0≪ -C1≪C2≪ … ≪Cl-1≪ -Cl≪ 1.同样可使M(h,δ)在h=0 附近有l+1 个正的单根.又由于则当m为奇数时，有 0＜-b0≪ -b1≪ … ≪ -bk≪ 1（l为偶），或 0＜b0≪b1≪…≪bk≪1（l为奇）.再根据（5）式知，M+(h,δ)在h=0 附近可出现个负的单根.然而，当m为偶数时，有 0＜-b0≪b1≪-b2≪ … ≪(-1)k+1bk≪1（l为偶），或 0＜b0≪ -b1≪b2≪…≪(-1)kbk≪1（l为奇）.由此可知，M+(h,δ)在h=0 附近不能出现负根.综上可知，当l=k(m+1)+n,k≥0,0≤n＜m时，系统（1）在擦边闭轨L+0 附近可分支出个极限环.

（2）当l=k(m+1)+m,k≥0 时，根据（7）式，我们可选择C0,C1,C2,…,Cl满足 0＜-C0≪C1≪-C2≪… ≪Cl-1≪ -Cl≪ 1，若l为偶数；0＜C0≪-C1≪C2≪ … ≪Cl-1≪ -Cl≪ 1，若l为奇数，由（6）式知，M(h,δ)在h=0 附近可有l+1 个正的单根.再由于，以及定理1.1，同（1）可证M+(h,δ)可有个负的单根.所以，当l=k(m+1)+m,k≥0 时，系统（1）在擦边闭轨L+0 附近可分支出个极限环.证毕.

3 应用例题

考虑如下分片光滑Liénard系统

易见系统（35）|ε=0有一个由H+(x,y)=y4+x2-x=0 定义的擦边闭轨且m=2.下证系统（35）在附近可分支出5个极限环.实际上，由（5）和简单的计算得

其中

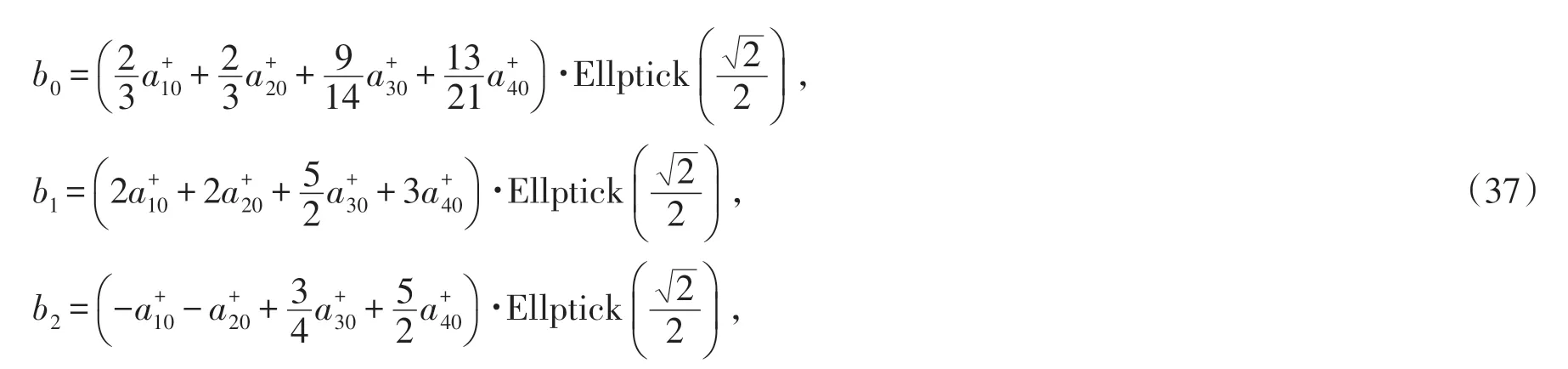
同（18）-（30），关于系统（35）有

和

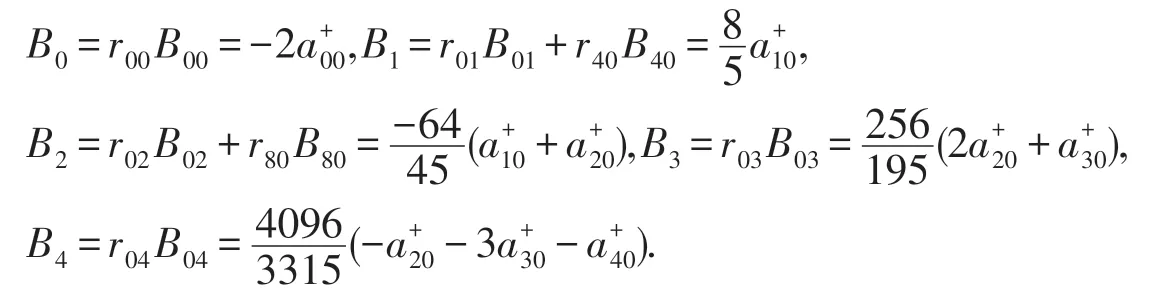
由引理2.5知

再由（36）和（38），

将（39），（40）代入（10），并应用定理1.1可知

其中

由（37）和（42）可得

当C0=C1=C2=C3=C4=0 时，有因此由定理 1.2（1），这里m=2,l=4,k=1,n=1, 当附 近 存 在使得系统（35）在擦边闭轨附近有5个极限环.

［1］COLL B，GASULL A，PROHENS R.Degenerate Hopf bifurcations in discontinuous planar systems［J］.J Math Anal Appl,2001,253：671-690.

［2］CHEN X，DU Z.Limit cycles bifurcate from centers of discontinuous quadratic systems［J］.Comput Math Appl,2010,59：3836-3848.

［3］LIU X，HAN M.Bifurcation of limit cycles by perturbing piecewise Hamiltonian systems［J］.Int J Bifurct Chaos Appl Sci Eng,2010,5：1-12.

［4］LLIBRE J，MAKHLONF A.Bifurcation of limit cycles from a two-dimensional center insideRn［J］.Nonlinear Anal,2010,72：1387-1392.

［5］HAN M.On Hopf cyclicity of planar systems［J］.J Math Anal Appl,2000,245：404-422.

［6］HAN M，CHEN J.On the number of limit cycles in double homoclinic bifurcations［J］.Sci China Ser A，2000：914-928.

［7］HAN M.Cyclicity of planar homoclinic loops and quadratic integrable systems［J］.Sci China Ser A，1997：1247-1258.

［8］LIANG F，HAN M.Limit cycles near generalized homoclinic and double homoclinic loops in piecewisesmooth systems［J］.Chaos Solitons Fract,2012,45：454-464.

［9］HAN M，ZHANG W.On hopf bifurcation in nonsmooth planar systems［J］.J Differ Equat，2010,248：2399-2416.