相容半Scott拓扑
2015-07-04李海龙姜广浩占诗源张鹏垚
李海龙,姜广浩,占诗源,张鹏垚
(淮北师范大学 数学科学学院,安徽 淮北 235000)
1 前言
由于Scott,Lawson,Plotkin等人的工作,连续格理论引起人们的广泛兴趣[1-3].Scott拓扑是domain上最重要的内涵拓扑之一,且在连续domain上又有一些较好性质.1997年,赵东升[4]基于半素理想,将连续格推广到半连续格.2008年,毕含宇等[5]在完备格上引入了半Scott拓扑,并讨论在半连续格上的一些性质.受到以上作者的启发,本文在相容完备格上引入相容半Scott拓扑,讨论它在相容半连续格上的若干性质.
定义1.1[6]设L是格,I⊆L是理想,若对任意x,y,z∈L,当x∧y∈I,x∧z∈I时有x∧ (y∨z)∈I,则称I为L的半素理想.Rd(L)表示L中所有半素理想构成的集合.
2 相容半Scott拓扑
定义2.1设L是格,∀x,y∈L,如果对 ∀S∈Rd(L),若 supS存在,且y≤ supS,有x∈S.则称x弱 ⇐关系y,记为x⇐wy.
定义2.2设L是格,S∈Rd(L)称为L的相容半素理想,如果存在x∈L使得S是L的相容半素理想}.
例1格L如图1所示:
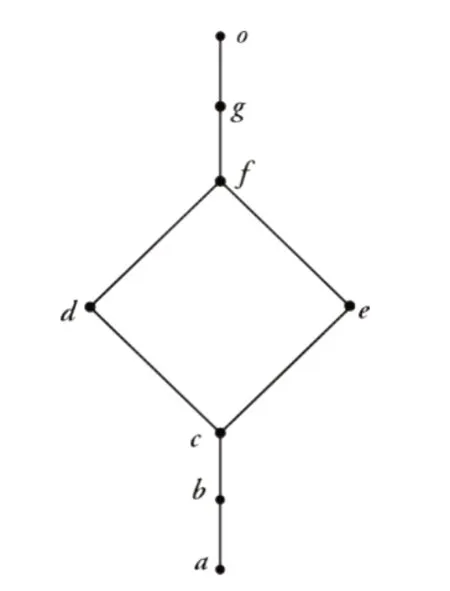
图1 S={a,b,c}是L的相容半素理想
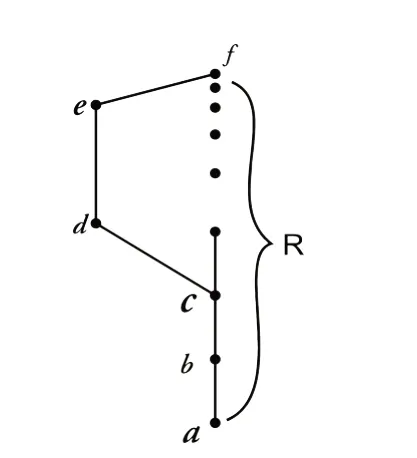
图2 R={a,b,c,d,e}是半素理想,但不是相容半素理想
例2格L如图2所示:
定义2.3若格L中任意相容半素理想都有并和交,则称L是相容完备格.
定义2.4设L是相容完备格,∀x,y∈L,x称为相容⇐关系y,记为x⇐cy,如果对∀S∈Ic(L),若y≤supS有x∈S.记为 ⇓cy={x∈L:x⇐cy}.
定义2.5设L是相容完备格,若对 ∀x∈L有x≤sup ⇓cx,则称L为相容半连续格.
定义2.6设L是相容完备格,U⊆L,若满足(1)U=↑U,(2)若 ∀S∈Ic(L),supS∈U⇒U⋂S≠ ∅,称U为相容半Scott 开集.L中相容半Scott 开集构成的拓扑称为相容半Scott 拓扑,记为σc(L).相容半Scott开集的补集称为相容半Scott闭集.
相容完备格L的子集X称为具有性质(M),若X满足:∀S∈Ic(L),若 supS∈X,则 ∃y∈S,使 ∀x∈S,x≥y⇒x∈X.
定理 2.1设L为相容完备格,A⊆L,若A为相容半Scott 闭集⇔A为下集且对相容半素理想并封闭.
证明设A为相容半Scott闭集⇔LA为相容半Scott开的⇔LA是上集且∀S∈Ic(L), 若 supS∈LA,有LA⋂S≠ ∅ ⇔A为下集且 ∀S∈Ic(L), 若LA⋂S=∅ 有 supS∉LA.⇔A为下集且 ∀S∈Ic(L),若S⊆A有supS∈A.⇔A为下集且对相容半素理想并封闭.
定理2.2设L为相容完备格,A⊆L,若A为相容半Scott开集⇔A为上集且有性质(M).
证明“必要性”A为相容半Scott 开集,则A是上集且∀S∈Ic()L,若 supS∈A,有A⋂S≠ ∅ .从而∃y∈A⋂S,对 ∀x∈S,x≥y,由A是上集知x∈A,故A具有性质(M).
“充分性”由A具有性质(M),则 ∀S∈Ic()L,若 supS∈A,则 ∃y∈S,使∀x∈S,x≥y有x∈A.从而A⋂S≠ ∅,故A为相容半Scott开集.
定理 2.3设L为相容完备格,则L的任一下集都具有性质(M).
证明设A为L的任一下集,∀S∈Ic()L,若 supS∈A,由A为下集,故 ∀x∈S有x∈A.故A有性质(M).
定理2.4设L为相容完备格,若存在相容半Scott开集U使y∈U⊆↑x,则x⇐cy.
证明设存在相容半 Scott 开集U,使y∈U⊆↑x,∀S∈Ic()L,若y≤supS,由U为上集,有supS∈U,又由U为相容半Scott开的,有U⋂S≠ ∅ .即 ∃z∈U⋂S,由U⊆↑x,有x≤z∈S.又S为下集,于是有x∈S,由⇐c的定义知x⇐cy.
定理2.5设L是相容完备格,∀x∈L,⇓cx为L的相容半素理想.
证明首先证 ⇓cx为理想,对 ∀a∈⇓cx,∀b∈L,若b≤a,由定理2.1 知b∈⇓cx,故 ⇓cx为下集,对∀y,z∈ ⇓cx,由 ⇐c的定义知 ∀S∈Ic(L),x≤supS有y,z∈S.由S为理想,故y∨z∈S,从而y∨z∈⇓cx,所以 ⇓cx为理想.再证 ⇓cx为半素理想.设a∧b∈⇓cx,a∧c∈⇓cx,由 ⇐c的定义知,对 ∀S∈Ic(L),若x≤ supS有a∧b∈S,a∧c∈S.由S为半素理想,有a∧ (b∨c)∈S.再由 ⇐c的定义知a∧ (b∨c)∈ ⇓cx,故⇓cx为半素理想.
下证 ⇓cx为相容半素理想.∀a∈⇓cx,由 ⇐c的定义知,∀S∈IU(L),若x≤supS,有a∈S.从而⇓cx⊆S,又S为相容半素理想,从而∃b∈L使得S⊆⇓cb,即 ⇓cx⊆⇓cb,故 ⇓cx为相容半素理想.
定理2.6设L为相容半连续格,则对∀U⊆σc(L)有U⊆⋃{⇑cx:x∈U}.
证明,由L为相容半连续格,则x≤sup ⇓cx,由U为上集知 sup ⇓cx∈U,由定理2.5知 ⇓cx∈Ic(L),又由U为相容半Scott开的,所以有 ⇓cx⋂U≠∅ .设y∈⇓cx⋂U,即y∈⇓cx且y∈U,从而x∈ ⇑cy,y∈U,故U⊆ ⋃{⇑cx:x∈U}.
定理2.7设L为相容半连续格,则对 ∀x∈L,有L↓x∈σc(L).
证明显然L↓x为上集,设 ∀S∈Ic(L),若 supS∈L↓x,假设S⋂(L↓x)=∅ .则有S⊆↓x,从而 supS≤ sup ↓x=x矛盾.所以S⋂ (L↓x)≠∅,从而L↓x为相容半Scott开集.
定义2.7设L是相容半连续格,f:L→Q是保序映射,若对 ∀S∈Ic(L)有f(s upS)=supf(S),且↓f(S)∈Ic(Q),则称f为强相容半连续的.
定义 2.8设L,L′为相容半连续格,映射f:L→L′关于相容半Scott拓扑连续,则称f是相容半Scott连续映射.
定理2.8设L,L′为相容半连续格,若f:L→L′是强相容半连续的保序映射,则f为相容半Scott 拓扑连续.
证明对 ∀U⊆σc(L′),由f保序知,f-1(U)为L的上集.设 ∀S∈Ic(L),若 supS∈f-1(U),由f为强相 容 半 连 续 的,有f(s upS)=supf(S)=sup ↓f(S)∈U,且 ↓f(S)∈Ic(L),由U⊆σc(L′),有↓f(S)⋂U≠∅,从而 ∃x∈↓f(S)⋂U,于是 ∃s∈S,使x≤f(s),即f(s)∈↑x⊆U,从而s∈f-1(U),故S⋂f-1(U)≠∅,由相容半Scott 开集定义知,f-1(U)为L的相容半Scott 的开集,从而f为相容半Scott 拓扑连续.
[1]BARANGA A.Z-continuous posets[J].Discrete Math,1996,152:33-45.
[2]ABRAMSKY S,JUNG A.Domain theory.Handbook of logic in comuter sci(vol.3)[M].Oxford:Clarendon Press,1994.
[3]GIERZ G.A compendium of continuous lattices[M].Cambridge:Cambridge University press,2003.
[4]ZHAO D.Semicotinuous lattice[J].Algebraic Universalis,1997,37(4):458-476.
[5]毕含宇,徐晓泉.半连续格上的半Scott拓扑与半Lawson拓扑[J].模糊系统与数学,2008,22(2):75-81.
[6]李高林,徐罗山,陈昱.半连续格上的半基和局部半基[J].模糊系统与数学,2010,24(1):51-55.
