标准马蹄形断面正常水深的直接近似计算公式

李风玲,文 辉

(惠州学院建筑与土木工程系,广东惠州 516007)

标准马蹄形断面正常水深的直接近似计算公式

李风玲,文 辉

(惠州学院建筑与土木工程系,广东惠州 516007)

针对目前标准马蹄形断面正常水深计算过程烦琐、公式复杂的缺陷,对标准马蹄形断面均匀流基本方程进行数学变换,根据水工隧洞设计规范的要求和工程实际应用情况确定公式的适用范围,应用拟合优化原理得到标准马蹄形断面正常水深的简捷、实用的计算公式。计算结果表明:在工程常用范围内计算的正常水深最大相对误差为0.585%,整个区间内95%以上的计算点相对误差小于0.20%,精度较高,能够满足工程实践的需要。

标准马蹄形断面;正常水深;直接计算公式;无量纲水深;水力计算

目前国内外学者对输水隧洞工程的圆形、蛋形、城门洞形等断面形式的水力计算问题进行了较为深入的分析和研究,也得到了许多简捷计算公式,解决了不少常规算法存在的工程实际问题[1-11]。马蹄形断面隧洞力学条件好、水力学条件优越,特别适合于围岩压力大的地质情况,是水利水电工程最常用的断面形式之一。为了满足工程建设的需要,自20世纪80年代就开始了标准马蹄形断面的水力计算研究,较好地解决了相关工程问题[12-18],但也存在着以下缺陷:①公式应用范围被无限地扩大,最大无量纲水深竟达1.85,远超出规范的上限要求,无法满足无压明流的条件;最小无量纲水深太小,也严重脱离工程实际需要。②公式大多为对应3种水深工况下的分段函数,使用时首先需要进行判别,然后选择对应的公式,最后才能得到结果,计算过程烦琐。③过分追求计算精度也导致公式形式较复杂。郑博等[19]较好地解决了标准马蹄形断面的临界水深计算,但关于正常水深的直接计算未见报道。本文从马蹄形断面均匀流基本方程出发,依据给水排水工程规范及水利工程规范等要求,考虑工程实际情况,合理地确定公式的应用范围,对无量纲水深和无量纲参数之间的关系进行研究分析,应用优化拟合方法,得到马蹄形断面正常水深的直接近似计算公式,为标准马蹄形断面的工程设计和运用提供参考。

1 标准马蹄形断面的构成及其水力要素

1.1 断面构成

马蹄形断面是由1个底弧、2个圆弧侧拱和1个圆弧顶拱构成,如图1所示。图1中h为过水断面对应的水深,m;r为顶拱半径,m;R为两侧拱半径和底拱半径(标准Ⅰ型马蹄形断面R=3r、标准Ⅱ型马蹄形断面R=2r),m;θ为底拱的弦对应的圆心半角或两侧拱对应的圆心角,rad;β为过水断面底拱对应的圆心半角,rad;γ为过水断面侧拱对应的圆心角,rad;φ为过水断面顶拱对应的圆心角,rad; e为标准马蹄形断面的底拱高度,m。

图1 标准马蹄形过水断面

1.2 水力要素

过水断面面积A、湿周χ及水深h分别为

1.3 无量纲水深表达式

设无量纲水深X为水深与断面顶拱半径之比:

3种不同水深条件下的未知圆心角就可用无量纲水深来表示:

式中Xe为标准马蹄形断面的无量纲底拱高度。

1.4 计算公式适用范围

从理论上讲,无量纲正常水深的取值范围应是[0,2]。根据DL/T 5195—2004《水工隧洞设计规范》[20],为了保证无压隧洞能在水位变化或波浪起伏的情况下仍能保持无压流状态,要求通过最大流量时洞内水面以上的空间面积不小于隧洞横断面面积的15%,净空高度大于0.40m,即

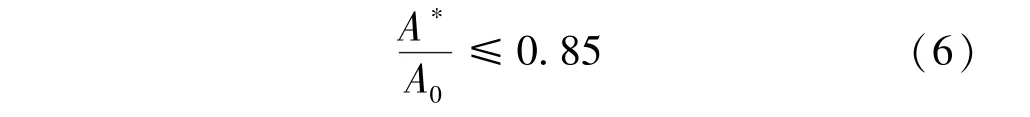
将φ=0代入式(1),得马蹄形全断面面积A0:

计算通过最大流量时洞内过水断面面积A*,有

式中φ*为通过最大流量时洞内过水断面顶拱对应的圆心角,rad。

将式(7)和式(8)代入式(6),可得三角超越方程:

方程(9)无法直接求解,经过试算:当标准Ⅰ型马蹄形断面t=3时,φ*=1.9468,代入式(2)得无量纲水深的上限值X*=1.563;当标准Ⅱ型马蹄形断面t=2时,φ*=1.9310,代入式(2)得无量纲水深的上限值X*=1.569。

考虑到适当外延,马蹄形断面无量纲水深的上限值统一取1.60;根据绝大多数工程实际应用情况,过小水深是没有工程实际意义的,无量纲水深的下限值统一取0.20,故确定的无量纲水深计算公式的工程适用范围为[0.20,1.60]。

2 标准马蹄形断面的简化计算公式

2.1 正常水深的基本方程

根据DL/T5195—2004《水工隧洞设计规范》和工程实际要求,马蹄形过水断面隧洞必须是无压流动,应按恒定均匀流计算,采用以曼宁公式表示的明渠均匀流方程计算其正常水深。

式中:Q为流量,m3/s;i为隧洞底坡比降;n为糙率系数。

2.2 正常水深的隐函数表达式

将式(5)代入式(1)～(3),再代入式(10)并整理,可得标准马蹄形断面无量纲正常水深的隐函数表达式:

2.3 正常水深的简化计算公式

为了方便研究,将式(11)左侧的已知量设为无量纲参数,即

本文以幂函数构造计算公式形式,通过进行大量试算,并采用编程逐步优化拟合的方法,得出标准无量纲正常水深的近似计算公式,定义Ⅰ型、Ⅱ型马蹄形断面无量纲正常水深分别为XnⅠ、XnⅡ。

标准Ⅰ型马蹄形断面无量纲正常水深的简化计算公式为

标准Ⅱ型马蹄形断面无量纲正常水深的简化计算公式为

3 公式评价

给出范围为[0.20,1.60]的无量纲正常水深X,由式(11)和式(12)求得无量纲参数M,由式(13)或

公式(13)和式(14)均为简单的幂函数形式,不是分段函数表示,不需通过判别适用范围来选择公式,因此简捷实用。通过对工程常用范围(0.2≤h/r≤1.6)的10000个计算点进行观察得出:求解正常水深的最大相对误差为0.585%,其中95%以上的计算点相对误差小于0.20%,精度较高,完全满足工程实践的需要。

4 实例应用

某输水隧洞拟采用标准Ⅰ型马蹄形断面,Q= 32m3/s,r=1.5m,i=0.006,n=0.014。由式(12)求得参数M=1.961 669;由式(13)求得无量纲正常水深XnⅠ=1.513 644;由式(4)求得正常水深hnⅠ= 2.270m(试算的精确值为2.271m),相对误差为-0.04%。

图2 计算误差分布

5 结 语

目前对于标准马蹄形断面的正常水深计算仍是十分复杂而烦琐的问题。本文对正常水深均匀流基本方程进行变换,用幂函数构造直接计算公式形式,运用拟合原理,提出了标准马蹄形断面正常水深的直接计算公式,所得公式不是分段函数,不需通过条件判别来选取计算公式,直接计算即可得到结果,简捷、方便、实用。在工程适用范围(0.20≤X≤1.60)内,求解正常水深的最大相对误差为0.585%,其中超过95%的计算点其相对误差绝对值小于0.20%,精度较高,完全满足工程实际需要。

[1]李风玲,文辉,彭波.圆形过水断面临界流的近似水力计算[J].人民长江,2008,39(11):77-78.(LIFengling, WEN Hui,PENG Bo,et al.Approximate hydraulic calculation for critical flow in circular cross-section[J]. Yangtze River,2008,39(11):77-78.(in Chinese))

[2]张宽地,吕宏兴,赵延风.明流条件下圆形隧洞正常水深与临界水深的直接计算[J].农业工程学报,2009,25 (3):1-5.(ZHANG Kuandi,LÜHongxing,ZHAO Yanfeng.Direct calculation for normal depth and critical depth of circular section tunnel under free flow[J]. Transactions of the Chinese Society of Agricultural Engineering:Transactions of the CSAE,2009,25(3):1-5. (in Chinese))

[3]文辉,李风玲.再论圆管明渠均匀流正常水深的直接计算公式[J].水利水电科技进展,2012,32(6):15-17. (WEN Hui,LIFengling.Further study on explicit formula for normal water depth of uniform flows in circular pipes [J].Advances in Science and Technology of Water Resources,2012,32(6):15-17.(in Chinese)).

[4]李风玲,文辉,涂宁宇蛋形断面管道正常水深近似算法[J].人民长江,2008,39(18):77-78.(LI fengling, WEN Hui,TU Ningyu.Approximate calculation approach of normalwater depth in an egg-shape pipe[J].Yangtze River,2008,39(18):77-78.(in Chinese))

[5]文辉,李风玲,李霞,等.蛋形断面管道临界水深的近似算法[J].人民黄河,2008,30(12):111-112.(WEN Hui,LI fengling,LIXia,et al.Approximate calculation of critical depth of oval section pipe[J].Yellow River, 2008,30(12):111-112.(in Chinese))

[6]马吉明,谢省宗,梁元博.城门洞形及马蹄形输入隧洞内的水跃[J].水利学报,2000,31(7):20-24.(MA Jiming,XIE Shengzong,LIANG Yuanbo.Hydraulic jumps in rectangular conduit with circular upper wall and horseshoe tunnel[J].Journal of Hydraulic Engineering, 2000,31(7):20-24.(in Chinese))

[7]王正中,陈涛,张新民,等.城门洞形断面隧洞临界水深度的近似算法[J].清华大学学报:自然科学版,2004, 44(6):812-814.(WANG Zhengzhong,CHEN Tao, ZHANG Xinming,et al.Approximate solution for the critical depth of a arched turnel[J].Journal of Tsinghua University:Science and Technology,2004,44(6):812-814.(in Chinese))

[8]文辉,李风玲,欧军利,等.城门洞形断面隧洞正常水深的近似算法[J].给水排水,2007,33(7):18-21.(WEN Hui,LIFengling,OU Junli,et al.Approximate solution of the normal depth inside tunnel with arch cross-section [J].Water and Wastewater Engineering,2007,33(7): 18-21.(in Chinese))

[9]文辉,李风玲.再论城门洞形断面隧洞正常水深的近似计算[J].给水排水,2008,34(11):42-43.(WEN Hui, LI Fengling.Discussion again of the approximate calculation for the normal water depth of the city-opening Section Tunnel[J].Water and Wastewater Engineering, 2008,34(11):42-43.(in Chinese))

[10]文辉,李风玲再论城门洞形断面隧洞临界水深的近似计算[J].人民长江,2009,40(11):78-79.(WEN Hui, LI Fengling.Discussion on approximate calculation of critical water depth in U-shape cross-section tunnel[J]. angtze River,2009,40(11):78-79.(in Chinese))

[11]赵延风,刘军,梅淑霞,等.普通城门洞形断面正常水深的近似计算方法[J].武汉大学学报:工学版,2009 42 (6)773-775.(ZHAO Yanfeng,LIU Jun,MEI Shuxia,et al.Approximatemethod for calculating normalwater depth in common city-opening shaped cross-section[J]. Engineering Journal of Wuhan University,2009,42(6): 773-775.(in Chinese))[12]王正中,陈涛,芦琴,等.马蹄形过水断面临界水深的直接计算[J].水力发电学报,2005,24(5):95-98. (WANG Zhengzhong,CHEN Tao,LU Qin,et al.The direct solution on critical depth of horseshoe section tunnel [J].Journal of Hydroelectric Engineering,2005,24(5): 95-98.(in Chinese))

[13]张宽地,吕宏兴,陈俊英.马蹄形过水断面临界水深的直接计算法[J].农业工程学报,2009,25(4):15-18. (ZHANG Kuandi,LÜHongxing,CHEN Junying.Direct calculation of critical depth of horseshoe section tunnel [J].Transactions of the Chinese Society of Agricultural Engineering,2009,25(4):15-18.(in Chinese))

[14]刘计良,王正中,赵延风.马蹄形隧洞断面收缩水深的迭代法计算[J].农业工程学报,2010,26(增刊2): 167-171.(LIU Jiliang,WANG Zhengzhong,ZHAO Yanfeng.Iterative calculation for contracted depth of horseshoe tunnel cross-section[J].Transactions of the Chinese Society of Agricultural Engineering,2010,26 (Sup2):167-171.(in Chinese))

[15]文辉,李风玲,李霞.标准Ⅰ型马蹄形断面正常水深的近似算法[J].人民黄河,2008,30(7):89-90.(WEN Hui,LIFengling,LIXia.Approximate solution on normal depth of standard I type horseshoe section tunnel[J]. Yellow River,2008,30(7):89-90.(in Chinese))

[16]赵延风,王正中,芦琴.马蹄形断面正常水深的直接计算公式[J].水力发电学报,2012,31(1):173-178. (ZHAO Yanfeng,WANG Zhengzhong,LU Qin.Direct calculation formulae for normal depth of horseshoe section [J].Journal of Hydroelectric Engineering,2012,31(1): 173-178.(in Chinese))

[17]文辉,李风玲.平底马蹄形断面的水力计算[J].农业工程学报,2013,29(10):130-135.(WEN Hui,LI Fengling.Hydraulic calculation of horseshoe cross-section with flat-bottom[J].Transactions of the Chinese Society of Agricultural Engineering,2013,29(10):130-135.(in Chinese))

[18]文辉,李风玲.平底Ⅰ型马蹄形断面临界水深的直接求解[J].长江科学院院报,2013,30(4):40-43.(WEN Hui,LI fengling,Direct solution to the critical depth of I-type horseshoe cross-section with flat bottom[J].Journal of Yangtze River Scientific Research Institute,2013,30 (4):40-43.(in Chinese))

[19]郑博,滕凯.马蹄形隧洞过水断面临界水深的简化计算方法[J].中国水能及电气化,2012,90(8):7-11. (ZHENG Bo,TENG Kai.Simplified calculation method of criticalwater depth on the U-shaped tunnel water passing cross-section[J].China Water Power&Electrification, 2012,90(8):7-11.(in Chinese))

[20]DL/T 5195—2004 水工隧洞设计规范[S].

The exp licit formula for normal water depth in the standard horseshoe cross-section

LI Fengling,WEN Hui (Department of Architecture and Civil Engineering,Huizhou University,Huizhou 516007,China)

The calculation formula of normalwater depth in the standard type horseshoe cross-section presents shortcomings such as complicated formula and cumbersome process.To overcome this,herewemathematically transform the fundamental equations of uniform flow in the standard type horseshoe cross-section tunnels.By determining the range of the formula according to the hydraulic tunnel design specification and engineering application,we obtained a simple and feasible calculation formula for normal water depth in the standard type horseshoe cross-section tunnels based on the principle of optimization.Results showed that themaximum relative error of normal water depth was 0.585%in the utility range,and the relative error over 95%of the whole range was less than 0.20%.The proposed formula satisfies the needs of engineering practice due to its high accuracy and simple form.

standard horseshoe cross-section,normal water depth,direct calculation formula,dimensionless depth; hydraulic calculation

TV131.4

A

1006-7647(2015)02-0043-04

10.3880/j.issn.1006 7647.2015.02.009

2013-12-02 编辑:周红梅)

惠州学院引进教授、博士科研启动基金(C510.0211);惠州学院重点培育学科项目(ZDPYXK1404)

李风玲(1964—),女,重庆梁平人,副教授,主要从事水力学研究。E-mail:mmlflmm@163.com