定向井破裂压力计算方法及其应用

2015-07-02周林帅

石油地质与工程 2015年1期

关键词：定向井斜角方位角

周林帅，徐超，刘伟，尚睿

(胜软油气勘探开发研究院，山东东营 257000)

定向井破裂压力计算方法及其应用

周林帅，徐超，刘伟，尚睿

(胜软油气勘探开发研究院，山东东营 257000)

针对目前定向井破裂压力计算模型不完善的现状，开展了任意井斜和方位的破裂压力计算研究，依据破裂压力的计算原理及椭圆有关理论，建立了斜井、水平井不同井斜和方位的破裂压力计算公式。利用推导的计算方法对不同井型目的层破裂压力进行了计算，并与现场施工测量的数据进行对比，两者相对误差不超过5%，表明该计算方法具有较高的可靠性。

定向井破裂压力；计算方法；压力模型

近几年，国内外诸多学者对斜井、水平井水力压裂做了一些机理研究[1-4]，并建立了定向井破裂压力的计算模型。目前，针对定向井的破裂压力计算仍多采用传统经典Hubbert-Willis模型、Eaton模型、Stephen模型等[5-9]。然而，定向井涉及的计算参数较多，特别是新加入了井斜角、方位角等影响因素，使得破裂压力计算更加复杂[10]。但从总体看，对任意井斜、方位破裂压力精确求解的研究还不够深入。笔者汲取了有关学者的理论研究模型，结合实际经验，推导出了斜井、水平井任意井斜和方位的破裂压力计算模型。

1 定向井应力分析

定向井应力计算需考虑井眼的轨迹，不同的井斜和方位沿井筒方向的应力发生变化，造成其破裂压力随之而改变。根据直角坐标系与地应力坐标系之间的转换关系[11](图1)，将井筒直角坐标系转化为地应力坐标系(图1中坐标系(σx、σy、σv)分别与水平最大主应力、水平最小主应力、上覆压力一致，直角坐标系(x、y、z)中，oz对应井轴，ox、oy位于与井轴垂直的平面内)。根据椭圆参数理论方程，实现了定向井地应力坐标系下任意方位应力求解。

(1)

式中：σA——任意方位的应力，MPa；σx——水平最大主应力，MPa；σy——水平最小主应力，MPa；θ——井轴线水平面投影与水平最大主应力夹角，度。

2 定向井破裂压力计算模型

地层深部存在三个相互垂直的主应力系统，即上覆地层压力σv、水平最大主应力σx及水平最小主应力σy。从岩石力学角度看，地层压裂是由于井内压力过大使岩石所受的周向应力超过岩石的抗拉强度而造成的[12]。根据应力与应变关系，当有效切应力与岩石抗拉强度之和为零时，地层就发生破裂，此时泥浆柱的压力即为地层破裂压力：

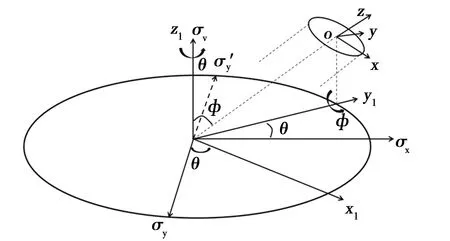
图1 斜井井眼坐标与地应力坐标关系

Pf=3σy-σx-αPp+σT

(2)

式中：Pp——地层孔隙压力，MPa；σT——岩石抗拉强度，MPa；α——Biot系数。

2.1 斜井破裂压力计算

在借鉴有关学者[13]所推导出的破裂压力公式基础上，根据椭圆有关理论的核心算法，再与(2)式相结合得到斜井任意方位、任意井斜的破裂压力计算公式(θ为相对方位角；φ为井斜角 )。

(1)当斜井井筒轴线方向在水平面上的投影与水平最大主应力方向的夹角θ=0°，且0<φ≤90°，此时，与井轴方向垂直的应力除水平最小主应力σy之外，还与垂直且过水平最小主应力面内的应力有关，即与水平最大主应力σx和垂向应力σv有关，因此，破裂压力的计算公式可表示为：

Pf1=3σy-(σxcos2φ+σvsin2φ)-αPp+σT

(3)

(2)当斜井井筒轴线方向在水平面上的投影与水平最大主应力方向的夹角θ=90°，且0<φ≤90°，此时，与井轴方向垂直的应力除水平最大主应力σx之外，还与垂直且过水平最大主应力面内的应力有关，即与水平最小主应力σy和垂直应力σv有关，因此，破裂压力的计算公式可表示为：

Pf2=3σx-(σycos2φ+σvsin2φ)-αPp+σT

(4)

(3)如果斜井井筒轴线方向在水平面上的投影与水平最大主应力方向的夹角不是上述两种情形，依据应力关系及椭圆参数方程，将(3)和(4)式代入(1)式，建立了适合任意井斜和方位的破裂压力计算公式,即为：

(5)

2.2 水平井破裂压力计算

水平井井斜角φ接近或达到90°，其井眼直角坐标与地应力直角坐标关系如图2所示，图中σx、σy分别与水平最大主应力、水平最小主应力方向一致，θ为井眼轨迹方向与水平最大主应力方向的夹角(即为相对方位角)。

根据地应力坐标系与直角坐标系之间的转换关系，由付永强等[14]所建立的水平井破裂压力公式，与式(2)相结合得到：

(1)当水平井井眼轨迹方向与水平最大主应力方向的夹角θ=0°时，即水平井井眼轨迹沿着水平最大主应力方向，此时上覆应力σv和水平最小主应力σy垂直于井轴线，则破裂压力的计算公式表示为：

Pf1=3σy-σv-αPp+σT

(6)

(2)当水平井井眼轨迹方向与水平最大主应力方向的夹角θ=90°时，即水平井井眼轨迹沿着水平最小主应力方向，此时上覆应力σv和水平最大主应力σx垂直于井轴线，则破裂压力的计算公式表示为：

Pf2=3σx-σv-αPp+σT

(7)

(3)但大多数情况下，水平井井眼轨迹方向不一定完全沿着水平最小主应力钻进。因此，导致其与水平最大主应力方向夹角不是90°，而是一个锐角，此情形下井筒的应力状态变得更加复杂。根据椭圆相关理论及应力之间的关系，推导得出垂直于井眼轨迹方向的应力σA(图2)，其表达式为：

(8)

图2 水平井井眼坐标与地应力坐标关系

根据三应力之间的关系，此时垂直于水平井水平段轨迹的应力分别为上覆应力σv和σA。由破裂压力的计算公式可知：

Pf=3σA-σv-αPp+σT

(9)

将(7)式代入(8)式得到水平井水平段任意相对方位角下破裂压力计算公式：

(10)

3 破裂压力变化特征分析

地下岩体受构造运动的影响，造成各地区所受的构造应力有所不同，则形成的正断层、逆断层及走滑断层所控制区域的破裂压力随着井筒井斜角变化而改变。根据上述破裂压力随着井斜和方位的变化关系式，将水平最大主应力、垂向应力及破裂压力对水平最小主应力作归一化处理，分析相对方位角变化时，井筒井斜角与破裂压力之间的变化关系，以有效掌握定向井破裂压力的变化特征。

图3为井筒相对方位角(井轴在水平面上的投影与水平最大主应力夹角)分别为0°、15°、45°、60°、75°、90°时破裂压力随着井斜角变化的关系，由图3表明：逆断层控制的应力区域随着井筒井斜角的增加，破裂压力增加；走滑断层应力控制区域随着井筒井斜角的增加，破裂压力增加(井筒相对方位角小于60°时)，但和逆断层相比，破裂压力增加较慢；当井筒相对方位角大于75°时，随着井筒井斜角增大，破裂压力有减小的趋势；当井筒的相对方位角为90°时，随着井筒井斜角的增大，其破裂压力明显呈减小趋势；正断层控制的应力区域破裂压力随着井筒井斜角的增加，破裂压力减小。对于正断层、逆断层及走滑断层，在井筒井斜角不变时，破裂压力随着垂向应力的增大而减小。

图3 破裂压力与井斜角和方位角的关系

4 实例应用

依据建立的任意井筒井斜角和方位角下的破裂压力计算模型，对胜利等多个油田的若干口井进行试算，将计算结果与实际测量值进行了对比分析。

A井是胜利油田某区块的定向井，为砂泥岩储层。该井现场实施了井底压力计监测，当目的层段地层破裂时，井底压力计数据显示破裂压力为61.5 MPa，如图4(a)所示，其压力计监测值基本可以代表实际地层的破裂压力。

在3 234 m射孔深度处，计算得到的水平最小主应力为49.5 MPa，水平最大主应力为66.0 MPa，泊松比为0.25，杨氏模量为2.16×104MPa，地层破裂压力为60.0 MPa,如图4(b)所示。计算值与井底压力计所测得的数据基本吻合，证明该项技术计算破裂压力的可靠性。

图4 定向井破裂压力计算成果图

通过对多口不同岩性井下压力计的实际监测数据与应用该项技术计算的破裂压力进行比对，两者数据吻合较好，相对误差不超过5%。表1为实际监测与计算的破裂压力对比情况。

5 结论

(1)本文依据椭圆参数方程，建立了定向井地层破裂压力的计算模型，可以适用于任意井斜及任意方位破裂压力计算。

(2)在不同的构造应力下，随着方位角和井斜角的变化，破裂压力也发生变化；对于逆断层，破裂压力随着井筒方位角的增大而增大；对于正断层，破裂压力随着井筒方位角的增大而减小；而对于走滑断层，随着井筒方位角和井斜角的增大，破裂压力先增大后减小。针对水平井，井筒的方位角与水平最大主应力制约着破裂压力的变化，当方向一致时，其破裂压力最小。