PM2.5影响因素的主成分回归分析与预测
2015-07-02王翠云胡学平相旭东
王翠云 ,胡学平,相旭东
(安庆师范学院 数学与计算科学学院,安徽 安庆246133)
PM2.5影响因素的主成分回归分析与预测
王翠云 ,胡学平,相旭东
(安庆师范学院 数学与计算科学学院,安徽 安庆246133)
应用主成分分析和多元回归分析法对空气质量指数(AQI)进行分析,首先对数据进行Alpha可靠性分析、主成分分析得到两个主成分变量,进而对它们和PM2.5浓度进行多元回归分析,并且进行显著性检验,发现PM2.5与这两个主成分变量具有线性回归关系,最终得到一个1-α的置信区间,从而结合实际提出一些降低PM2.5浓度的对策。
PM2.5;Alpha可靠性分析;主成分分析;多元回归分析
近年来,空气质量不断下降,作为最能代表空气质量的PM2.5指数,被人们广泛关注。影响PM2.5指数的因素有很多,要分析这一问题必需降维,而主成分回归模型是一种降维模型,被普遍应用于各行各业的学术分析以及科学研究。降维后的变量线性无关,所代表的信息不会彼此重复,且几乎代表全部原始信息,这也是它在很多研究领域中得到应用的根本原因。如程毛林[1]利用主成分的线性及非线性回归模型对经济增长的边际效应和弹性效应做了具体分析,对经济学的效应分析有一定的参考作用;蒋云波等人[2]对上市公司的绩效评价建立了主成分模型,得到了71家IT行业上市公司的模型结果,即绩效评价,这种绩效评价方法为其他行业公司提供了很好的参考;何畅[3]则通过应用主成分分析法找出影响CPI指数的主要影响因素,这为下一步通过时间序列方法来解析CPI指数与宏观经济走势之间的紧密联系以及进一步为国家或者个人的预判起到了很好的铺垫作用。
本文利用主成份分析和多元回归分析法,对某市2013年1月1日到5月31日的AQI数据进行分析,通过探究O3-1h,O3-8h,CO,PM10,SO2,NO2,T等7项主要指标与PM2.5之间的关系,获得一个多元回归方程。从而根据某一时刻的上述各项数据来预测PM2.5的浓度及其未来变化趋势。先分析Alpha可靠性。
假设I) 模型只考虑PM2.5与O3-1h,O3-8h,CO,PM10,SO2,NO2,T有相关关系。
假设II) 假设O3-1h,O3-8h,CO,PM10,SO2,NO2,T对PM2.5的影响无多重共线性。
所提供的样本并不能直接说明PM2.5浓度只与O3-1h,O3-8h,CO,PM10,SO2,NO2,T这7个变量有相关关系,那么这些数据对于PM2.5的分析是否可靠性,则需要用Alpha可靠性分析进一步度量。由SPSS软件对本文数据进行Alpha可靠性分析结果如表1所示。
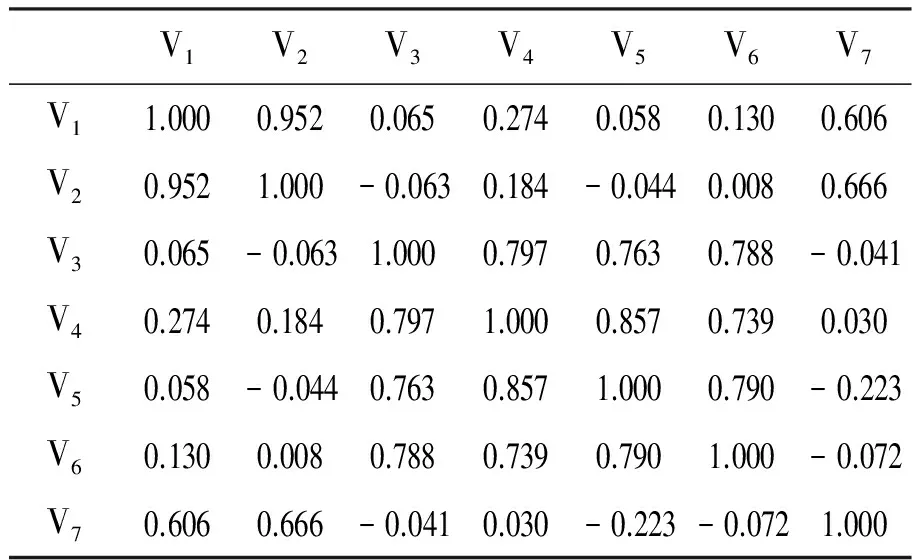
表1 相关矩阵
由表1中各个变量的相关矩阵,可见V1与V2的相关程度最密切(r=0.952)。Cronbachα系数[4]即通过所得数据表取得真分数的概率,它也是对数据以及一切项目的评定成绩的相关系数的平方。由表2可知,在数据的信度检验中,Cronbachα系数为0.757,开方为0.87,可信度很高,此AQI数据可靠,可以用来对PM2.5进行分析以及预测。下面给出具体的过程。
1 主成分分析
主成分分析[5]是确定研究问题、选定变量后,确定几个线性无关且包含极可能多原始变量信息的新变量来替换原始变量。设X1,X2,X3,…,Xp为影响PM2.5的p个随机自变量,记X=(X1,X2,…,Xp),协方差矩为∑=(σji)p×p=E[X-E(X)][X-E(X)]T。记∑的特征值为λ1≥λ2≥…≥λp≥0及其相应的正交单位化特征向量为e1,e2,…,ep,则由文献[6]可知:
X的第i个主成分为
Yi=eiTX=e1iX1+e2iX2+…+epiXp,i=1,2,…,p,且有
由以上分析知PM2.5与O3-1h,O3-8h,CO,PM10,SO2,NO2,T这7指标之间有着相关关系,然而,这些样品的某些观测指标和其所属类型没有必然的逻辑关系,因此通过SPSS软件用主成分分析的方法来分析这7个指标对PM2.5的影响。
令V1:变量O3-1h;V2:变量O3-8h;V3:变量CO;V4:变量PM10;V5:变量SO2;V6:变量NO2;V7:变量T;Y:变量PM2.5

表3 总方差解释

表4 主成分矩阵
表3分析了每个主成分的特征根及其代表原始信息的能力, 特征根大于1的主成分变量一般是SPSS软件保留的,本表中特征根大于1的主成分有2个,它们共代表了原始信息的84.74%,已足够起到对影响PM2.5的因素进行分析及对PM2.5浓度进行预测的作用,因此本文只保留了2个主成分。由表4给出了这两个主成分的各个系数,因此可以得到这两个主成分的表达式如下。
第一主成分变量:
由表3可知,第一主成分含有所有原变量48.6%的信息量。而它与变量O3-1h成正比例,即当O3-1h含量每增加1单位时,第一主成分变量会相应增加0.212单位;同理,当O3-8h含量每变化1单位时,它会相应变化0.089单位;依此类推,当温度T增加1度时,第一主成分变量反而会减少0.051单位。可见,PM10对第一主成分的影响最大,而温度T对它影响最小,且成反比例变化。
第二主成分变量:
同理,由表3可知,第一及第二主成分含有所有原变量84.7%的信息量,且由主成分分析法的根本可知这两个主成分无线性相关性。因而第二主成分变量分别与O3-1h,O3-8h,PM10,T这4个影响因素呈正相关关系,而与CO,SO2,NO2这3个影响因素呈反比例关系,且它受O3-8h影响最大,受NO2的影响最小。
2 多元线性回归分析
前节已将原始7个自变量通过“浓缩”为Y1,Y2这两个主成分变量,降低了分析和解决问题的难度。下面则需要检验Y和Y1,Y2之间是否具有线性关系,然后再通过SPSS对它们做多元线性回归分析。首先,作Y和Y1,Y2的线性图和散点图,分别如图1、图2。
由图1和图2分析可知: Y和Y1,Y2之间具有明显的线性趋势。
因此,接着用SPSS对Y和Y1,Y2进行多元线性回归分析[7],结果如表5。

表5 方差分析

表6 模型总结

表7 回归系数
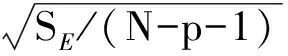
由方差分析表5可知,回归方程的临界显著性水平SignificanceF也小于0.000 1,因而是极高度显著地。由表7给出的回归方程的各回归系数可得线性回归分析结果为
Y1,Y2代入可得下式:
12.428V3*+12.905V4*+12.692V5*+
12.406V6*-0.561V7*
由于所有的多元回归系数,例如3.086,1.395等,都是去除所分析变量和其他自变量对Y的公共影响后,分析变量对Y的边际影响,因此,PM2.5与O3-1h,O3-8h,CO,PM10,SO2,NO2这6个变量都成正相关,显然PM10对PM2.5浓度的相关性最大,其系数为12.905,因此在预防PM2.5对大气的影响之前,首先需要控制对PM10的排放;其次,CO,SO2对PM2.5的相关性次之,则O3-8h最小,最小并不代表可以任其在大气中排放,这4个因素的浓度增加会使PM2.5浓度呈正相关的变大,进而影响空气质量;最后温度T与PM2.5浓度呈负相关关系。因此,湿度、温度、压强、O3-1h,O3-8h等影响因素的浓度不同,它们对大气环境中PM2.5的浓度的影响也不同。因此,为了减少空气中可吸入颗粒物的浓度,首先需要减少石油及煤炭等的燃烧,提高其利用率,严格控制并尽量减少生活中SO2,PM10及CO的排放量,并且能适当的调节城市温度等外界条件,或者在天气寒冷的时候做好对PM2.5浓度升高的准备,从而降低PM2.5对市民的生活、城市的发展可能造成的恶劣影响。
3 显著性检验
通过P值检验法[8],由第2节的多元线性回归分析的SPSS计算结果可得回归方程检验的P值为0.000α,因而回归方程是极高度显著的;再由Y1,Y2的检验结果, P值分别为0.000,0.125,可知两个解释变量Y1,Y2的作用都是显著的,所得回归方程可以用来预测。下面来对其进行预测。
4 PM2.5值的统计学预测
当给定解释变量的一组取值(v01,…,v07)时,根据主成分方程可计算求得y01,y02,进而由回归方程可得Y的一个回归值:
它是对PM2.5:
y0=91.269+13.799y01+0.173y02+ε0
的一个点估计,所以y0的置信度为1-α的预测区间为
注 N为样本数目,p=2,
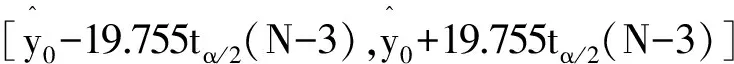
[1]程毛林. 基于主成分回归模型的经济增长因素分析[J]. 运筹与管理, 2012, 21(1): 175-179.
[2]蒋云波, 陈维政. 上市公司绩效评价模型构建研究[J]. 西南石油大学学报(社会科学版), 2010, 3(5): 73-78.
[3]何畅. CPI指数的主成分分析及对经济走势的影响[J]. 山西财经大学学报, 2011, 33(3): 47-53.
[4]郭惠昕, 戴娟, 唐蒲华, 等. 基于随机集的不完整信息可靠性分析方法[J]. 机械科学与技术, 2011, 30(2): 290-296.
[5]杨淑菊. 主成分分析在学生成绩评价中的应用[J]. 数学的实践与认识, 2012, 42(16): 103-112.
[6]梅长林, 周家良. 实用统计方法[M]. 上海: 科学出版社, 2002: 53-60.
[7]张建同, 孙昌言. 以Excel和SPSS为工具的管理统计[M]. 北京: 清华大学出版社, 2005:18-24.
[8]姚菊香, 王盘兴, 鲍学俊, 等. 相关系数显著性检验的几何意义[J]. 南京气象学院学报, 2007, 30(4): 566-570.
Analyzing and Forecasting the Influence Factor of PM2.5 Based on Principal Component Regression
WANG Cui-yun, HU Xue-ping, XIANG Xu-dong
(School of Mathematics and Conputation Science,Anqing Teachers College, Anqing 246133, China )
By investigating the AQI data with Principal component analysis and Multivariate regression analysis, We get two kinds of statistical extrapolate and analysis results regarding the value of PM2.5. First, by means of Alpha reliability analysis and principal component analysis, we get two principal components. Then we analyze them and PM2.5 by multivariate regression analysis and we give it a test of significance. The testing provides strong evidence to suggest that there is indeed a significant linear regression correlation between them. A confidence interval about the value of PM2.5 is obstained. Some methods to reduce the PM2.5 can be put forward.
PM2.5, Alpha reliability analysis, principal component analysis, multivariate regression analysis
2015-04-01
安徽省高校自然科学基金重点项目(KJ2013A179)。
王翠云,女,河南信阳人,安庆师范学院经济与管理学院硕士研究生,研究方向为管理统计与企业发展;胡学平,男,安徽宿松人,博士,安庆师范学院数学与计算科学学院教授,研究方向为随机过程及应用。
时间:2016-1-5 13:01 网络出版地址:http://www.cnki.net/kcms/detail/34.1150.N.20160105.1301.007.html
F126.1
A
1007-4260(2015)04-0024-04
10.13757/j.cnki.cn34-1150/n.2015.04.007
