Fan-Todd不等式在矩阵论中的推广
2015-07-02金乐乐周其生
金乐乐 ,周其生
(安庆师范学院 数学与计算科学学院,安徽 安庆 246133)
Fan-Todd不等式在矩阵论中的推广
金乐乐 ,周其生
(安庆师范学院 数学与计算科学学院,安徽 安庆 246133)
利用矩阵迹的Cauchy-Schwarz不等式及性质,将著名的Fan-Todd不等式和与之相关的实数不等式推广到矩阵论中,得到矩阵迹的相应不等式,一些结论还推广到算子理论中。
矩阵;迹;Fan-Todd不等式;算子
作为矩阵的一个重要数字特征,矩阵的迹在数值计算、量子信息以及随机控制等方面有着广泛的应用。但是矩阵的乘法不具有交换性,许多实数不等式难以推广到矩阵论中。本文利用矩阵迹的Cauchy-Schwarz不等式及相关性质,将Fan-Todd等实数不等式推广到矩阵论中。
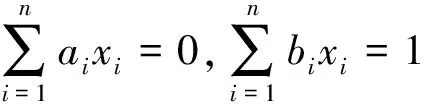
成立的任一实数序列,则

其中等式成立当且仅当
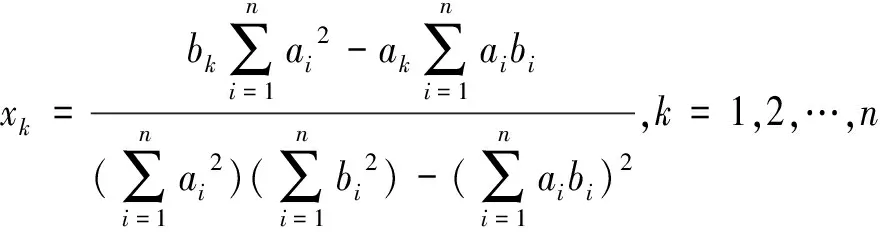
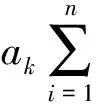
K.Fan等人利用这个定理证明了:
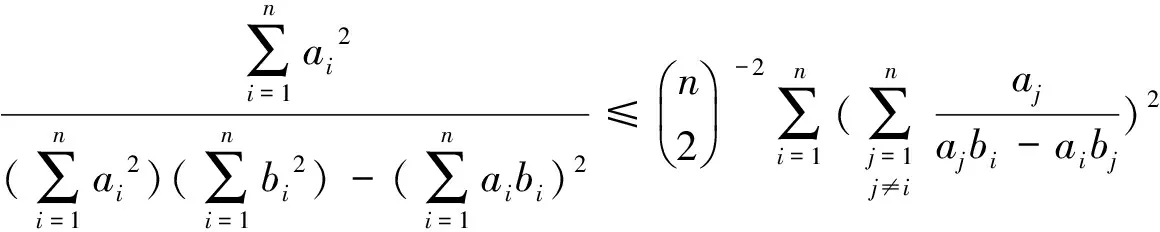
K.Fan等人对定理B作了进一步推广:

本文将以上几个不等式推广到矩阵论中,得到矩阵迹的相应不等式。先给出一个重要引理,即关于矩阵迹的Cauchy-Schwarz不等式:
引理1[5-6]设A,B为m×n复矩阵,则有
|tr(A*B)|2≤tr(A*A)tr(B*B),特别当A和B为同阶实对称阵或Hermite阵时
|trAB|2≤trA2·trB2,
等号成立当且仅当存在常数c,使得A=cB。
下面是本文的主要结论。
定理1 设A,B为n阶非零实对称阵,对于任意常数c,B≠cA,又令X为满足trAX=0,trBX=1的任一同阶实对称阵,则
(1)
(2)
证明 对于任意的y∈R,yA-B为实对称阵,由引理1得
|tr[(yA-B)X]|2≤tr(yA-B)2·trX2
(3)
即|tr(yAX-BX)|2≤tr(yA-B)2·trX2。又tr(yAX-BX)=ytrAX-trBX=-1,所以

这说明对任何实数y,二次不等式恒大于0,因此判别式Δ≤0,即
因为对任意常数c,均有B≠cA,故由引理1知,trA2·trB2>(trAB)2,所以化简后有

上述不等式即证。
下面讨论定理1中等号成立的条件。
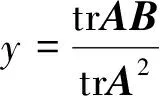
则(3)式等号成立(显然左边也算出等于1),故由引理1知,存在c使得X=c(yA-B)(其中c为实常数),即有
X2=c2(yA-B)2,

从而c2=(trX2)2,c=±trX2,故
X=±trX2(yA-B)。
当X=trX2(yA-B)时,
与定理条件不合,所以
X=-trX2(yA-B)=-trX2·
当(2)式成立时,不难计算(1)式等号成立。
注2 定理1是定理A的推广。为了看到这一点,令
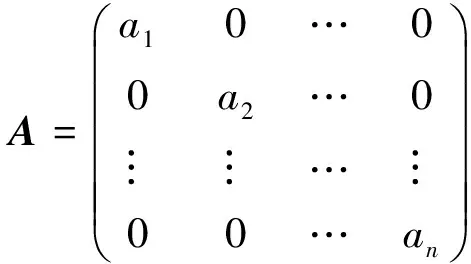


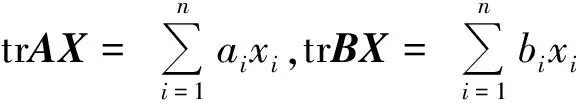
下面讨论A,B为n阶复矩阵时的情况。
定理2 设A,B为n阶非零Hermite阵,且不存在常数c使得B=cA,又设X为满足trAX=0,trBX=1的任一同阶Hermite阵,则

证明 任意y∈R,yA-B也为Hermite阵,由引理1得|tr[(yA-B)X]|2≤tr(yA-B)(yA-B)*·trXX*=tr(yA-B)2·trX2,其证明与定理1的证法类似。
是两个满足aibj≠ajbi(i≠j)的n阶Hermite阵,则


它的n(n-1)项可以按以下成对形式分组:
根据定理1,可以推出


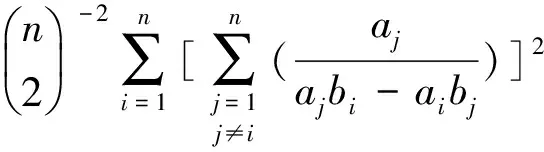
对定理3进行类似定理B到定理C的推广:
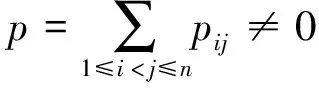
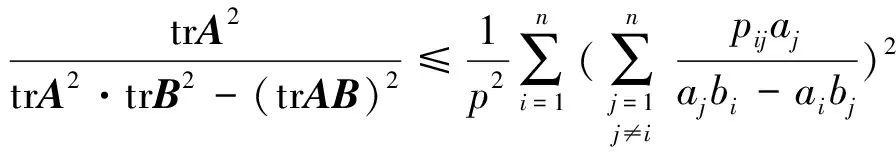
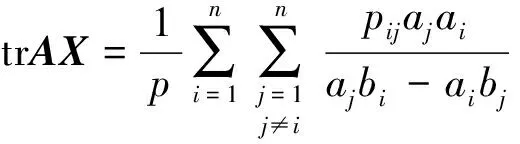
它的n(n-1)项可以按以下成对形式分组:
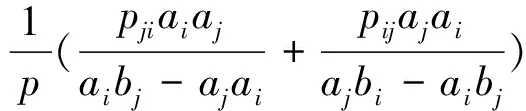
每一对这样的和等于零,即可推出trAX=0。同理可证,
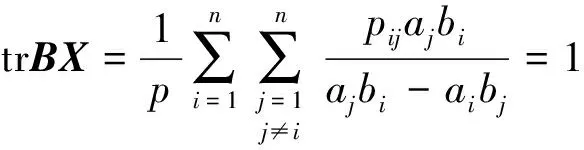
因而由(1)式可得上述定理。

即为定理3的结论,可见,定理4是定理3的推广。
类似于定理1的讨论,可将文献[5]中一个实数不等式推广为下面结论。
定理5 设A,B为n阶非零Hermite阵,且不存在常数c使B=cA,又设任一同阶半正定Hermite阵X,满足trX2=1,trA2>0,trAX=0,则
(4)
其中等号成立当且仅当
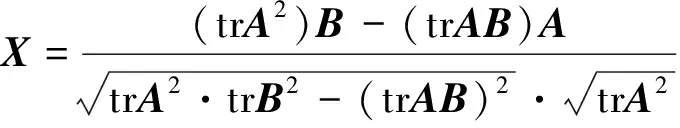
证明 任意y∈R,由引理1,得
|tr[(yA-B)X)]|2≤
tr(yA-B)(yA-B)*·trXX*
(5)
|tr[(yA-B)X)]|2=[ytrAX-trBX]2=
(0-trBX)2=(trBX)2,
tr(yA-B)(yA-B)*·trXX*=
tr(yA-B)2·trX2=y2trA2-2ytrAB+trB2,
所以有(trBX)2≤y2trA2-2ytrAB+trB2,
即对于∀y∈R有(trA2)y2-2(trAB)y+trB2-(trBX)2≥0成立。因此Δ≤0,即Δ=[-2(trAB)]2-4·trA2·[trB2-(trBX)2]≤0
即(trAB)2-trA2·[trB2-(trBX)2]≤0。
因为对任意常数c,均有B≠cA,故由引理1知,trA2·trB2>(trAB)2,所以有

下面讨论定理5中等号成立的条件。
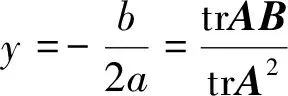
此时,tr(yA-B)2·trX2=tr(yA-B)2=
故(5)式等号成立,由引理1知,存在常数c,使得
X=c(yA-B),
trBX=c(ytrAB-trB2)=

因(trBX)2=tr(yA-B)2=
定理2讨论的是Hermite矩阵,定理2可以进一步推广到算子论中。
定理6 设A,B为非零Hilbert-Schmite类Hermite算子,且不存在常数c,使得B=cA。又设X为满足trAX=0,trBX=1的任一Hilbert-Schmite类Hermite算子,则

证明 记全体Hilbert-Schmite类算子为C2[7],任意y∈R,yA-B也为Hilbert-Schmite类Hermite算子,在C2类算子中定义内积
|
即|trA*B|2≤trAA*·trBB*。
特别地,当A,B为C2中Hermite算子时有|trAB|2≤trA2·trB2,所以|tr[(yA-B)X]|2≤tr(yA-B)(yA-B)*·trXX*=tr(yA-B)2·trX2。
此定理的证明与定理2的证明过程相同,因此可以将定理2推广至算子理论中。
[1]A. Ostrowski. Vorlesungen Über Differential-und Integralrechnung[M]. Basel: Springer, 1952.
[2] K.Fan , J.Todd. A determinatal inequality[J]. Journal of London Mathematics Society, 1955, 30: 58-64.
[3] D.S. Mitrinovic, P.M. Vasic. Analytic Inequalities[M]. New York: Springer-Verlag, 1970: 66-69.
[4] D.S. Mitrinovic. 解析不等式[M]. 张小萍, 王龙, 译. 北京: 科学出版社, 1987: 87-92.
[5] 匡继昌. 常用不等式[M]. 4版. 济南: 山东科技出版社, 2012: 201-202.
[6] 王松桂, 吴密霞. 矩阵不等式[M]. 2版. 北京: 科学出版社, 2006: 185-224.
[7] 孙善利, 王振鹏. 泛函分析[M]. 北京: 北京航空航天大学出版社, 2008: 117-135.
Generalization of Fan-Todd Inequality in the Matrix Theory
JIN Le-le, ZHOU Qi-sheng
(School of Mathematics and Computational Science, Anqing Teachers College, Anqing 246133, China)
In this paper, famous Fan-Todd real inequalities are generalized to the matrix by the Cauchy-Schwarz inequality, and some corresponding matrix trace inequalities are obtained.Some conclusions are given in operator theory.
matrix, trace, Fan-Todd inequality, operator
2014-12-23
金乐乐,女,安徽安庆人,安庆师范学院数学与计算科学学院硕士研究生,研究方向为矩阵与算子理论。
时间:2016-1-5 13:01 网络出版地址:http://www.cnki.net/kcms/detail/34.1150.N.20160105.1301.006.html
O151.21
A
1007-4260(2015)04-0019-05
10.13757/j.cnki.cn34-1150/n.2015.04.006
