基于震荡残差修正的灰色模型在堆场沉降预测中的应用

宋龙超　张光伟　覃晴

【摘 要】 以盐城港射阳港区某码头后方堆场为例，提出灰色模型GM（1，1）的震荡残差修正方法，对比分析双曲线法和原始灰色模型GM（1，1）二种方法。结果表明，经震荡残差修正后的原始灰色模型能够更精确地描述堆场的初期沉降现象，利用此模型可以获得更为可靠的最终沉降量。

【关键词】 码头堆场；沉降预测；灰色模型GM（1，1）；震荡残差修正

0 引 言

地基最终沉降量（尤其是工后沉降）是工程上十分重要的问题。在海港工程中，堆场陆域形成后常需进行地基处理，以避免场地后期大沉降现象的出现。对于地基沉降的计算或预测是判定地基处理成功与否的重要环节，国内外学者就此进行了大量的研究，这些计算方法可大致分为以下3类：

（1）《建筑地基基础规范》推荐的分层总和法；

（2）根据固结理论，结合土体的本构模型，采用数值计算土体最终沉降量的有限元法；

（3）根据前期沉降资料，建立预测模型，得出沉降规律及最终沉降量的模型预测法。

在模型预测法中，一般先要对地基处理后的沉降进行持续半年以上的观测，然后利用有限的前期观测数据建立相应的预测模型，预估地基沉降的发展趋势并推测出最终沉降量；因此，建立能够精确描述初期沉降现象的预测模型十分必要。

本文针对堆场沉降数据采用灰色模型GM 进行预测，观察到相应的预测残差更接近于震荡函数形式，进而引入新的二阶残差白化方程以描述这种震荡残差行为，最终得到更符合实测数据的预测结果。

1 预测模型的建立

本文将沿用灰色模型思想，着力描述GM模型残差的系统性变化规律。在大部分工程实践中，E（0）应该是一个绕0值上下震荡的序列，并保持一定的连续性；因此，可以使用正弦函数级数描述。基于这一思想，前人发展出傅立叶变换方案，以提取残差中反映系统偏差的内禀信息。但是，堆场沉降测量数据点一般偏少，数据周期性并不明显，傅立叶变换方案的直接应用可能使计算过程过于完备而掩盖了系统真实的震荡特性。考虑到沉降数据的有限性，为简化计算，直接假定残差序列对应一个单频的正弦函数

2 实例分析

2.1 样本数据的选取

码头位于盐城港射阳港区，拟建项目位于射阳河入海口左岸，后方场区与鱼塘堤围相接，码头前沿为射阳港出海航道。后方陆域布置有煤炭堆场、钢材堆场、一般件杂货堆场、集装箱堆场，以及生产、生活辅助区，陆域形成采用砂土回填，陆域堆场设计高程为5.4 m。根据设计技术要求，工程场地地基工后固结度要求达到80%以上，工后地基残余沉降值满足规范要求（工后残余沉降设计按小于30 cm控制）。

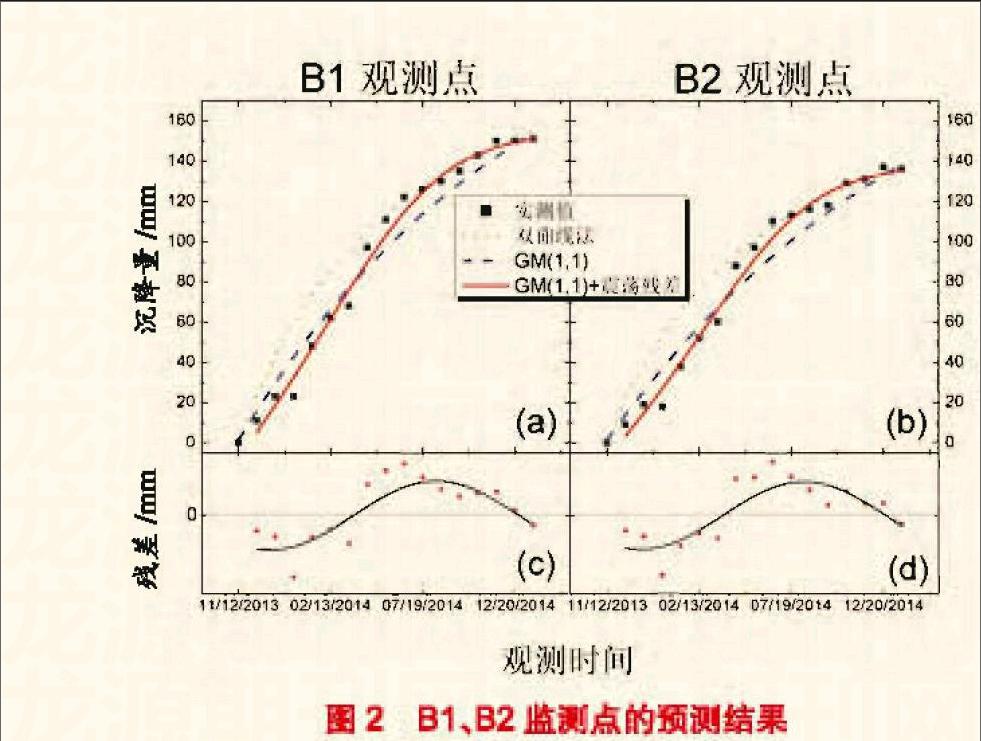
本文以煤炭北堆场工后沉降的实测数据（监测点B1，B2）作为样本进行研究，具体监测点见图1。监测时间为2013年11月12日至2015年1月21日，具体监测数据见表1。

2.2 计算结果及分析

针对沉降数据进行双曲线拟合及GM（1，1）预测，预测结果见表2，预测结果与实测数据对比见图2。双曲线法对后期沉降值有较好的描述，但前期预测值系统性地高于实测值；GM（1，1）预测则平衡了前期与后期沉降的误差分布，得到了适中的预测曲线。

需要注意的是，GM（1，1）的预测曲线并未完全地考虑到沉降现象在沉降监测前期与后期的不同。图2（c）（d）给出了GM（1，1）模型残差随时间的演变。以2014年5月为分界，在监测前期，GM（1，1）给出了较高的估计；而在后期，残差值演变行为完全相反。整个残差值演变出现系统性的震荡，符合本文提出的震荡残差修正方案的适用条件。

针对B1和B2两个监测点GM（1，1）预测的残差值进行震荡残差修正计算，计算得到震荡频率 分别为0.350和0.355（单位为月 1）。图2（c）（d）展示了计算所得震荡残差修正函数，计算震荡残差函数与的残差大致吻合，可以用于对的进一步改进。图2（a）（b）给出了考虑到震荡残差修正后的预测值。图2中多个模型预测的对比结果显示，在经过考虑震荡残差修正后，GM（1，1）可以更有效地避免系统性的误差偏离，得到最为吻合的预测曲线。

3 结 语

本文提出的GM（1，1）震荡性残差修正新方案，可为工程实践得到更高精度的初期沉降预测，有利于远期最终沉降值的验证工作。本方法充分考虑了GM（1，1）残差的震荡性质，避免了傅立叶变换冗繁的算法和复杂的数学理解，利用二阶白化方程，将计算过程线性化、解析化。运用双曲线法、GM（1，1）方法及GM（1，1）残差震荡修正方法，试验性地对盐城港射阳港区某码头后方煤炭北堆场监测点B1、B2进行预测，得到了最吻合实测值的预测曲线，证明该方案的有效性。