模型选择的逼近理想解排序方法

吴 喜

(阜阳师范学院 经济学院，安徽 阜阳 236037)

模型选择的逼近理想解排序方法

吴 喜

(阜阳师范学院 经济学院，安徽 阜阳 236037)

一般在使用模型选择准则下很难区分多个候选模型和在不同准则下会产生不同的组合模型，为了解决这个问题，文章引入一种包括平均绝对误差、均方误差、平均相对误差、一致性指标、相关系数、预测有效度的多准则的模型评价指标体系，在此基础上提出逼近理想解法模型选择方法。实例结果表明该方法合理和可行。

模型选择；逼近理想解；组合预测

模型选择是当今统计学和计量经济学界研究的国际前沿问题，统计学家们提出了许多模型选择的方法和准则，如逐步回归、AIC[1]、AICC[2]、BIC[3]等，根据这些方法和准则，可以从众多候选模型中选出适当的模型。如在建立ARMA模型预测时，常用AIC,AICC,或BIC等准则，比较每个候选模型的准则值，将准则值最小的模型作为最优模型。然而在实际建模中(尤其在小样本或中样本量场景下)，出现若干个候选模型的同一准则值彼此接近，很难以区分[4]。同时由于从不同类型模型(如线性回归、自回归等)及不同的角度(模型残差平方和最小及模型参数节约性等)提出的模型选择准则(AIC、BIC等)选择模型，会得到不同的候选模型。利用以上方法选择会导致模型的不确定性，此方法存在一些缺陷，此方面的论述可参见文献[5]。

目前解决模型选择的不确定性最常用的方法是模型组合，该方法关键在于如何确定组合预测权系数, 使得组合预测模型更有效地提高预测精度。国内学者从不同角度提出不同方法,如学者陈华友[6]给出了基于预测误差指标和基于预测有效度两大类组合权重准则建立组合模型；采用不同的准则会有不同的组合预测模型，其权重数的获取也就存在着一定的差异，得到不同的组合预测模型也不一样。

鉴于以上论述，模型选择遇到问题：第一，在针对单一候选模型，不同准则选出不同的模型，要从这些候选模型选最佳模型；第二，当对单一模型进行组合时，由于采用不同的准则导致对不同候选模型权重不一样, 当得到不同组合预测模型时，要对组合预测模型评价。部分学者对预测模型的评价仅从某个角度研究如王丰效[7]引入了组合预测模型点预测精度的数量指标，从而得到了组合预测模型的点预测精度向量给出了模型预测精度的评价。该方法仅从某一个角度选取单个指标对预测模型局部评价。目前很少有文献利用模型指标评价体系借助系统的思想从整体上对单一的候选模型或不同组合预测模型进行研究。

1 组合预测模型预测评价

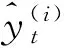
(1)平均绝对误差。由于预测误差有正有负，为避免正负相抵消，取误差的绝对值进行综合并计算平均，它是误差分析的综合评价指标之一。

(1)

(2)均方误差是预测误差的平方数之和的平均数，其表示如下

(2)

(3)平均绝对相对误差

(3)

(4)一致性指标。Theil不等系数是一种度量两个离散序列一致性指标，当两个序列越接近，Theil不等系数越接近于0，其公式如下

(4)

(5)相关系数

当预测值越接近实际值时，二序列的相关程度就越高，因而可以使用相关系数来度量预测的精确程度。其公式如下：

包括汪灏(1658-)，康熙四十二年(1703年)进士，著《知本堂读杜》，其中自序亦不无逢迎谢恩：“灏以书生，献赋行在所，蒙召试宫廷，屡试称旨，因得与科名备史馆，兢兢勤职，业日读书，以仰答主眷。 私衷窃欲于世所共尊众好之书之诗，以次渐读，而读杜为之先。”[24]211 可以理解的是，他们接受儒家事功理念积极入世，在清代学术风气转型中，以细密训诂集注的方式又使得注杜步入新的时期。

(5)

(6)预测有效度。预测有效度公式定义如下：

(6)

当有效度越高，预测效果愈好。

1.2 建立逼近理想解排序方法的组合预测评价模型

由于s个预测模型需要从多个属性指标系统评价，它可归结为多属性决策问题，本文借助多属性决策的一种方法，即逼近理想解排序方法，(Technique for order preference by Similarity to ideal solution)它是解决多属性问题的一种有效方法，简称TOPSIS法[9]。

理想解是一个理想状态最佳模型，它的各个指标都是评价矩阵中在该指标的最好值；而负理想解则是最差方案，它的每个属性值都是评价矩阵中该指标的最差的值。

该法的基本思想是:先找出组合预测模型在各个数量评价指标的理想解和负理想解,然后找出某个预测模型各个指标数值尽可能接近理想解而远离负理想解,它便是所要寻求的满意方案。

其方法步骤如下:

第一步:建立组合预测模型的评价矩阵A=(aij)s×m其中aij表示第i(i=1,2,…s)个组合预测模型在第j(j=1,2,…m)个评价指标取值。

第二步:把决策矩阵规范化,构成规范决策矩阵B=(bij)s×m。

(7)

第三步：求关于组合预测模型的理想解及负理想解。

(8)

其中J是正向目标集，J′是负向目标集。

正向目标集表示此指标越大越好，如相关系数、预测有效度；负向目标集表示此指标越小越好，如平均绝对误差、均方误差、平均相对误差、一致性指标。预测模型的理想解指在s个预测模型分别在平均绝对误差、均方误差、平均相对误差、一致性指标最小值，相关系数、预测有效度的最大值；预测模型的负理想解指在s个预测模型分别在平均绝对误差、均方误差、平均相对误差、一致性指标最大值，相关系数、预测有效度的最小值。

第四步，计算距离，每个解到理想解和负理想解的距离分别是

(9)

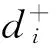
第五步，计算每个组合预测序列对理想解的相对接近程度。

(10)

显然，预测序列的各个指标离理想解越近而离负理想解越远，说明此预测模型越满意。

第六步，排列方案的优先次序。按di从小到大顺序排列，排在最前面的方案为最优方案。

2 应用实例

下面应用文献中说明逼近理想解在预测模型中评价的应用。文献[7]列出河南1980～1992年的数据研究了化工行业人才的组合预测问题，建立了三种单项预测模型，并给出预测结果和原始数据见文献.对于此文献中的数据，本文使用逼近理想解法对以上三种预测模型基于以上评价指标体系得到评价矩阵，然后对评价矩阵标准化得到计算结果如下。

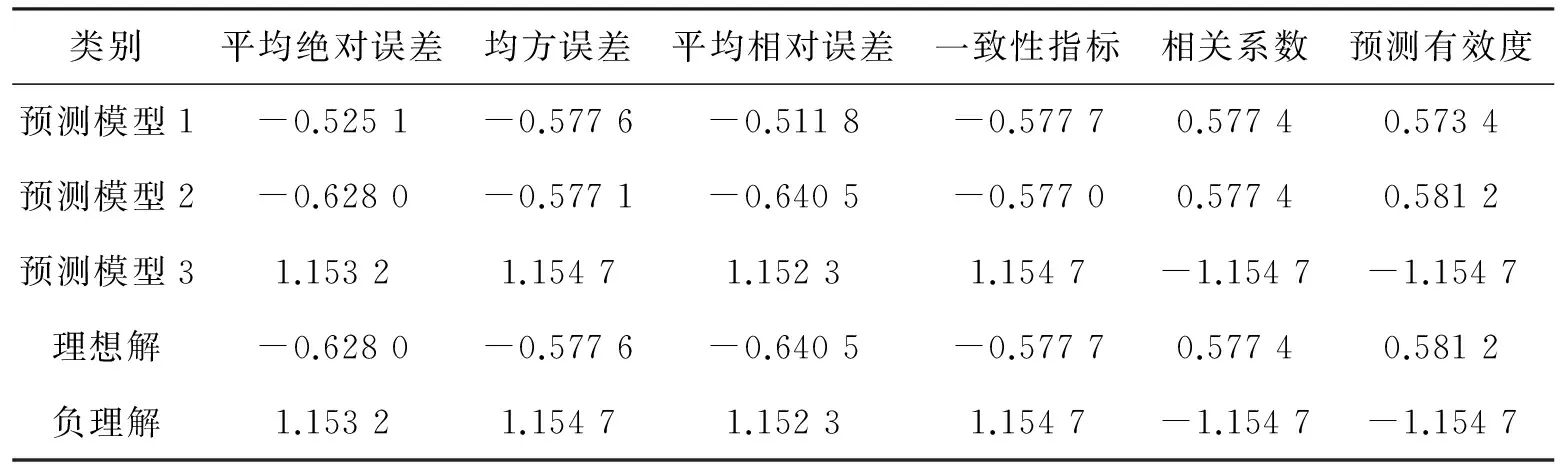
表1 三种单项预测模型的评价矩阵标准化

然后对表1采取上文的计算步骤，对每个预测模型进行排序，得到如下的结果：

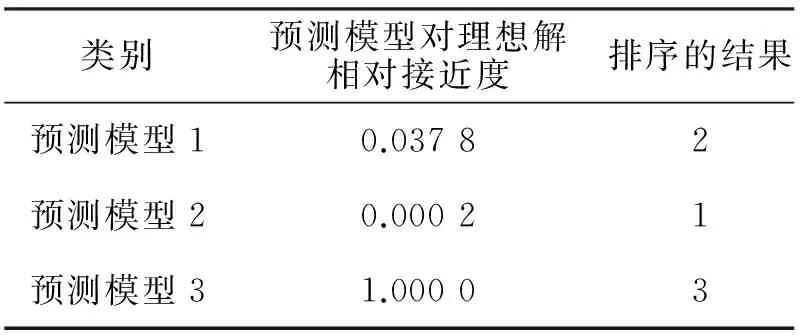
表2 每个预测方法对理想解相对接近程度

通过表2的结果可看出，利用逼近理想解法评价模型，明显预测模型2优于其它两个预测模型，预测模型1次之，预测模型3最差，这与文献[7]仅从预测模型的预测精度一致，但是本文提出是从多个方面考虑选择模型。我们继续使用文献[7]八种组合预测模型的数据进行评价，采用以上计算步骤进行分析，得到结果如表3。从表3可看出八种预测模型优劣排序为：预测模型8优于预测模型4优于预测模型1优于预测模型型3优于预测模型6优于预测模型2优于预测模型5优于预测模型7。该结果与文献[7]结果都认为模型8优于模型4，其他模型评价优先关系就不一致，但文献[7]仅从模型一个角度评价，该文提方法利用系统的思想却从多个角度评价模型。

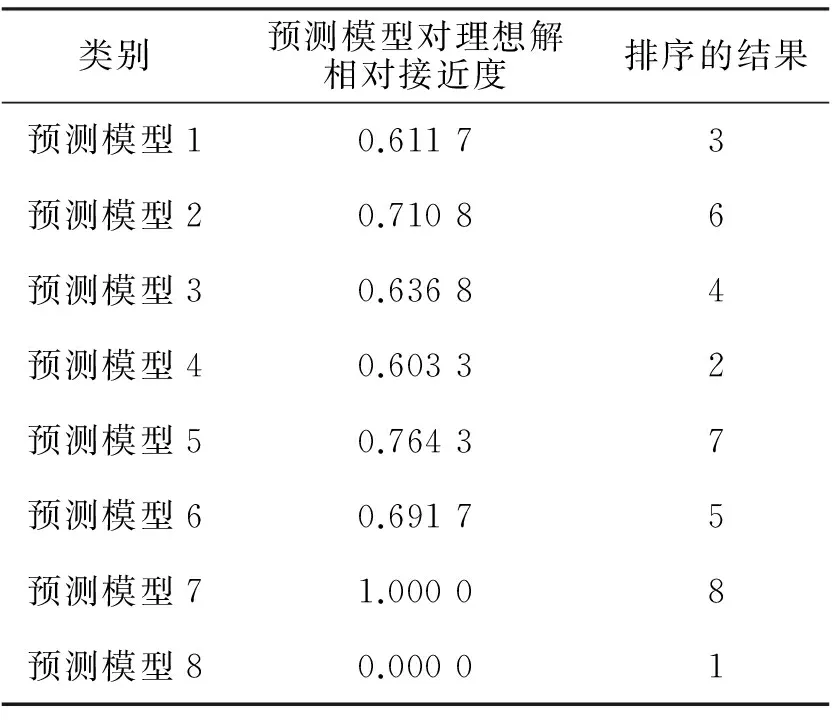
表3 八种组合预测模型对理想解的相对接近度

3 结论

随着学者对预测模型组合的的关注，越来越多组合预测模型权重确定的方法被提出，出现了多个候选模型问题，由于不同的模型选择方法和准则各有其优缺点，本文利用系统的思想提出逼近理想解的模型选择排序的方法，它的实质就是从多准则角度考虑选择不同方法构成的组合预测模型。最后通过应用实例说明本文方法的可效行和可行性。

[1] Akaike H. A new look at the statistical model identicaltion[J]. IEEE Transactions on Automatic control, 1974, 19(6): 717-723.

[2] Sugiura H. Further analysts of the data by Akaike's information criteria and the finite corrections[J]. Communication in Statistics-Theory and Methods, 1978, 7(1): 13-26.

[3] Schwarz G. Estimating the dimensional of a model,Annals of Statistics, 1978, 6(2),461-494.

[4] 吴 喜．时间序列模型选择的灰色关联法及其应用[J]．阜阳师范学院学报(自然科学版)，2012，29(3)：6-10．

[5] 张新雨，邹国华．模型平均方法及其在预测中的应用[J]．统计研究，2011，28(6)：97-102．

[6] 陈华友．组合预测方法有效性理论及其应用[M]．北京：科学出版社，2008：76-102．

[7] 王丰效．组合预测模型预测精度的贴近度评价法[J]．统计与决策，2013，380(8)：70-72．

[8] 周四清，王坚强．基于多准则优化的组合预测方法[J]．系统工程与电子技术，2009，31(7)：1651-1654．

[9] 岳超源．决策理论与方法[M]．北京：科学出版社，2003：212.

Model selection based on TOPSIS method

WU Xi

(SchoolofEconomics,FuyangNormalUninersity,FuyangAnhui236037,China)

It is generally difficult to distinguish candidate models and different combined models built by different criteria. In order to resolve this problem, this paper introduces multi-criteria model evaluation index system including mean absolute error, mean square error, mean relative error, consistency index, correlation coefficient, forecasting effectiveness. A method of model selection based on TOPSIS is proposed. By using the proposed method, the analysis results prove that the method is reasonable and effective.

model selection; TOPSIS; combined forecast

2015-01-21

阜阳师范学院自然科学研究项目(2011FSKJ10)；阜阳师范学院质量工程项目(2014JXTD01)资助。

吴 喜(1975-)，男，博士研究生，讲师,研究方向：决策科学理论。

O213;N949

A

1004-4329(2015)03-008-04

10.14096/j.cnki.cn34-1069/n/1004-4329(2015)03-008-04