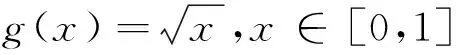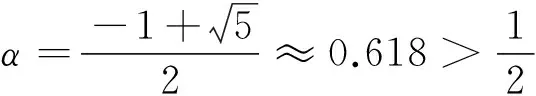Hermite-Hadamard模糊积分不等式的推广
2015-07-01姚云飞
葛 莉 ,姚云飞 ,刘 敏
(阜阳师范学院 数学与统计学院,安徽 阜阳 236037)
Hermite-Hadamard模糊积分不等式的推广
葛 莉 ,姚云飞 ,刘 敏
(阜阳师范学院 数学与统计学院,安徽 阜阳 236037)
研究Hermite-Hadamard模糊积分不等式的又一形式,估计Hermite-Hadamard模糊积分不等式的下界,举例说明下界的有效性。
模糊测度; 模糊积分; Hermite-Hadamard不等式
1 引言
模糊测度和模糊积分最初由学者Sugeno[1]提出,故模糊积分又称Sugeno积分。模糊积分受到了众多学者的关注,与模糊积分有关的一些不等式得到广泛研究。Ralescu和Adams[2]给出了几个模糊积分的等价定义,Wang和Klir[3]对模糊测度和模糊积分理论进行了概述。
近年来,许多学者研究了一些经典不等式在模糊积分下的形式[3-12]。 其中Caballero和Sadarangani[9]给出了模糊积分下的Hermite-Hadamard不等式,对函数在区间[a,b]上的模糊积分的上界进行估值。本文拟对[9]中的积分下界进行估值。
下面介绍一些基本概念和性质,详细内容见 [3]。
设∑为R的子集构成的σ-代数,μ:∑→[0,+∞)为非负的广义实值函数,称μ为模糊测度当且仅当
(1)μ(φ)=0;
(2)E,F∈∑且E⊂F,总有μ(E)≤μ(F);

(4){En} ⊂∑,若E1⊃E2⊃…⊃En⊃…,且μ(E1)<+∞,则

如果f是定义在R上的非负实值函数,对于α>0,Lαf={x∈X|f(x)≥α}={f≥α}表示f的α-水平集,L0f={x∈X|f(x)>0}=supp(f)表示f的支集。特别地,当α≤β时,{f≥β}⊂{f≥α}。
若μ为R上的模糊测度,定义Fμ(R)={f:R→[0,+∞)|f∈μ(R)}。
若μ为(R,∑)上的模糊测度,如果f∈Fμ(R),A∈∑,则定义在A上的关于模糊测度下函数f的模糊积分为
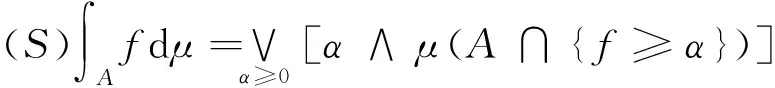
其中,∨,∧分别为在[0,+∞)上的上、下确界。
模糊积分的以下性质可参见文[3]。
性质1 如果μ为(R,∑)上的模糊测度,f,g∈Fμ(R),A∈∑,则
(1)(S) ∫Afdμ=μ(A);
(2)(S) ∫Akdμ=k∧μ(A),k为非负常数;
(3) 若在A上f≤g,则(S)∫Afdμ≤(S)∫Agdμ;
(4) 若A⊂B, 则(S)∫Afdμ≤(S)∫Bfdμ;
(5)μ(A∩{f≥α})≥α⟹(S)∫Afdμ≥α;
(6)μ(A∩{f≥α})≤α⟹(S)∫Afdμ≤α;
(7) (S)∫Afdμ<α⟺∃γ<α, 使得μ(A∩{f≥γ})<α;
(8) (S)∫Afdμ>α⟺∃γ>α, 使得μ(A∩{f≥γ})>α。
注 考虑到A上f的分布函数F,F(α)=μ(A∩{f≥α}),根据性质1(5)和(6),可以得到
F(α)=α⟹(S)∫Afdμ=α。
因而,从数值计算的角度,模糊积分可以通过求解方程F(α)=α计算。
Hermite[13]和Hadamard[14]给出了古典的Hermite-Hadamard不等式:
(1)
其中f:[a,b]→R且为上凹函数。
后来,不等式(1)在文[9]中得到推广和应用, Caballero 和Sadarangani给出了模糊积分下的Hermite-Hadamard不等式的几种形式,并对积分上界进行估计,本文将给出模糊积分下的关于下凹函数的Hermite-Hadamard不等式的另一形式,并对其积分下界进行估计。
2 主要结论
本文的主要结果为如下的三个定理。
定理1 设g:[0,1]→[0,+∞)且为下凹函数,满足g(0) 证明 由于g为下凹函数,则对∀x∈[0,1],有 g(x)=g((1-x)·0+x·1) ≥(1-x)g(0)+xg(1)=h(x)。 由性质1(3)得 由于 从而 注 在定理1中,若g(0)=g(1),其他条件不变,则h(x)=g(0), 从而 定理2 设g:[0,1]→[0,+∞)且为下凹函数,满足g(0)>g(1),g(1)>1,如果μ为R上的勒贝格测度,则 仿照定理1,同理可证。 定理3 设g:[a,b]→[0,+∞)且为下凹函数,μ为R上的勒贝格测度,则 (1) 若g(a) (2) 若g(a)=g(b)且g(a) (3) 若g(a)>g(b)且g(b) 证明 只证(1)。由于g为下凹函数,则对∀x∈[a,b],有 由于 F(α)=μ([a,b]∩{h≥α}) 求解方程F(α)=α,可得 从而 另一方面,由于 =μ([0,1]∩{x≥α2})=1-α2 例2 设g(x)=1-x2,x∈[0,1], 显然g在[0,1]上非负、下凹,由于g(0)=1,g(1)=0,根据定理2,可知 另一方面,由于 [1] Sugeno M. Theory of fuzzy integrals and its applications[D]. Ph.D.Thesis, Tokyo Institute of Technology, 1974. [2] Ralescu D, Adams G. The fuzzy integral[J]. Journal of Mathematical Analysis and Applications, 1980, 75: 562-570. [3] Wang Z, Klir G. Fuzzy measure theory[M]. Plenum, New York. 1992. [6] Mesiar R, Ouyang Y. General Chebyshev type inequality for fuzzy integrals[J]. Fuzzy Sets and Systems, 2009,160: 58-64. [7] Ouyang Y, Fang J. Sugeno interal of monotone functions based on Lebesgue measure[J]. Applied Mathematics and Computation, 2008, 56: 367-374. [8] Román-Flores H, Flores-Franulic A, Chalco-Cano Y. The fuzzy integral for montone function[J]. Applied Mathematics and Computation, 2007, 185: 492-498. [9] Caballero J, Sadarangani K. Hermite-hadamard inequality for fuzzy integrals[J]. Applied Mathematics and Computation, 2009, 215(6): 2134-2138. [10]Ouyang Y, Fang J X, Wang L S. Fuzzy chebyshev type inequality[J]. International Journal of Approximate Reasoning, 2008, 48(3): 829-835. [10]Caballero J, Sadarangani K. Sandor's inequality for Sugeno integrals[J]. Applied Mathematics and Computation, 2011,218(5): 1617-1622. [12]Hong, DH. A Liapunov type inequality for Sugeno integrals[J]. Nonlinear Analysis, 2011,74(18): 7296-7303. [13]Hermite C. Sur deux limites d'une integrale definie[J]. Mathesis 1883, 3:82. [14]Hadmard J. Etude sur les propietés des functions entiéres et en particulies d'une function considerée par Riemann[J]. Journal of Mathematical Analysis and Applications, 1893,58: 175-251. On the generalization of Hermite-Hadamard type fuzzy integral inequality GE Li,YAO Yun-fei,LIU Min (SchoolofMathematicsandStatistics,FuyangNormalUniversity,FuyangAnhui236037,China) In this paper, a new formula associated with Hermite-Hadamard type fuzzy integral inequality is provided, and the lower bound of the fuzzy integral inequality is obtained, and some examples are conducted to show the efficiency of the lower bound. fuzzy measure; fuzzy integral; Hermite-Hadamard inequality 2014-11-25 国家青年科学基金项目(11401104);国家级特色专业(TS11496);阜阳师范学院校级重点学科(2010XK6-03);安徽省高校优秀人才基金(2011SQRL099)资助。 葛 莉(1978-),女,硕士,副教授,研究方向:非线性泛函分析。 O159 A 1004-4329(2015)03-005-03 10.14096/j.cnki.cn34-1069/n/1004-4329(2015)03-005-03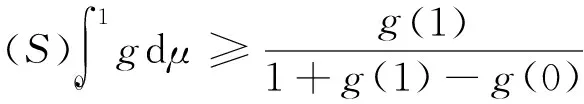
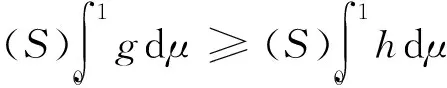
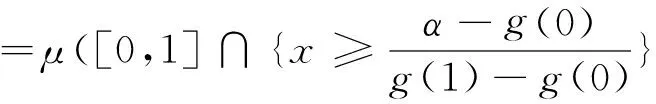
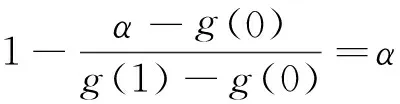

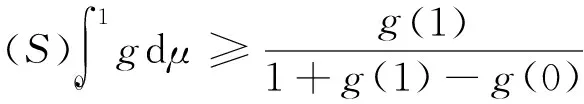

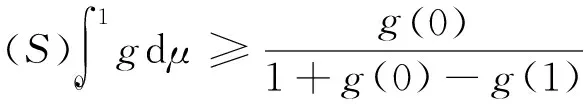

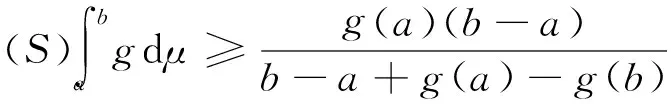

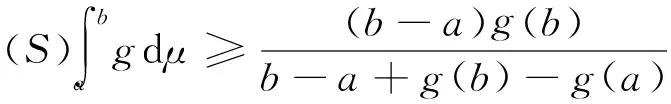
3 实例分析