喷嘴结构对水射流性能影响的分析
2015-07-01李俊张庆周一睁
李俊, 张庆,周一睁
(南京理工大学,江苏 南京 210094)
喷嘴结构对水射流性能影响的分析
李俊, 张庆,周一睁
(南京理工大学,江苏 南京 210094)
介绍了水射流理论及其计算流体力学的数学模型,运用FLUENT软件对不同结构喷嘴的水射流流场进行仿真分析。通过仿真结果比较得出:锥直形喷嘴整流段长度对喷射速度具有一定影响,且有利于喷嘴出口流量的增加;当喷嘴收缩角为14°时,水射流性能最佳。
水射流;喷嘴结构;流场仿真
0 序言
随着计算机和流体数值技术的快速发展以及许多湍流模型的成功建立,应用数值模拟的方法对水射流流动特性和物理量的分布规律进行研究具有更准确、可靠、迅速的优点。从20世纪30年代起,人们就利用理论,实验等多种手段对水射流进行了广泛的研究,而喷嘴是形成水射流的直接元件,其作用是将水的压力能转化为动能,因此喷嘴的结构直接决定着水射流的性能[1]。
1 水射流理论介绍
目前对于水射流已经形成了一套比较完整的分析方法。工程所用的水射流绝大数是湍流流动,其实际整体结构相当复杂,为了便于分析,众多学者将射流过程分为初始段、基本段、和耗散段3个阶段[2]。
初始段是射流的核心段,水流一离开喷嘴就与空气发生剧烈的动量交换和紊动扩散,但中心线附近的水射流在初始段仍保持喷嘴出口初始速度。初始段长度决定了水射流喷射的距离。
基本段是水射流的主体段,在这个阶段绝大部分为充分发展的紊动混掺区,且段内射流的轴向流速和动压力逐渐减少。
消散段也称为水射流的雾化段,此时射流已经变成水滴与空气的混合物或已雾化,轴向速度与动压力相对较低。
2 建立水射流数学模型
由于文中研究的是自由非淹没紊动射流,考虑水的粘性,且认为水射流过程中水流是不可压的。则在空间直角坐标系中,对于不可压流体,水射流连续方程为:
在空间直角坐标系中,对于不可压流体的N-S方程为[3]:
直接求解上述瞬态的控制方程难度很大,则采用时间平均处理的方法,从而引入了雷诺方程,雷诺方程相比N-S方程多了应力项,称为雷诺应力,此时形成的方程组不封闭,必须使用新的湍流模型使方程封闭,因此引入湍动能方程和湍流耗散率方程,便形成了不可压缩流体的标准k-ε模型[4]:
Gk+Gb-ρε-YM+Sk
其中:湍流粘度μt=ρCμk/ε,Gk为由平均速度梯度引起的湍动能的产生项;Gb为由浮力引起的湍动能的产生项;YM代表可压湍流中脉动扩张的贡献;C1ε、C2ε、C3ε为经验公式,σk和σε分别为与湍动能和耗散率对应的Prandtl数;Sk和Sε是用户定义的源项。
水射流基本方程由连续方程,雷诺方程和标准k-ε方程共同组成。
3 喷嘴的选择
喷嘴是形成水射流的核心部件。喷嘴结构主要指喷嘴的长径比、收缩角和流道形状[5]。不同结构的喷嘴所形成的流量系数,射流的扩散角和等速核长度都不相同。喷嘴的流道形状有椭圆形、流线型、圆弧型和锥形等,这些喷嘴的水力特性如表1。综合考虑喷嘴性能和加工,常使用锥形喷嘴,因此文中选择锥形喷嘴进行研究。当锥形喷嘴的收缩角取较大值时,在减小流体在喷嘴入口处的阻力的同时,也会使流动得不到充分发展,最终影响水射流的性能;当收缩角取值小时,又将给流动带来过大阻力。而锥直型喷嘴的整流段可改善流体从喷嘴中喷出前的状态,使喷出后的射流在空气中更稳定。
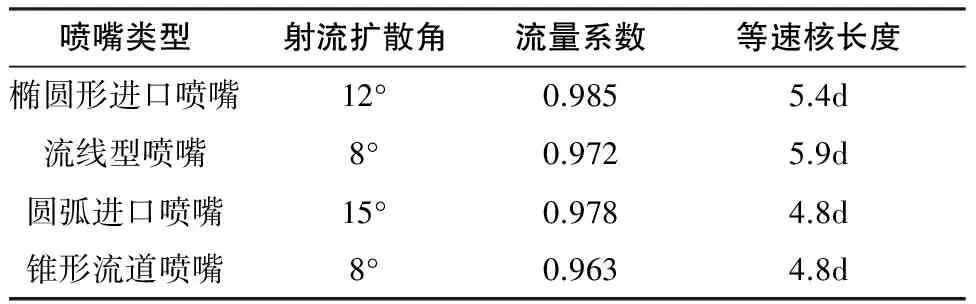
表1 各种喷嘴的水力特性对比
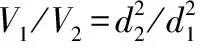
4 喷嘴射流流场仿真
4.1 几何建模与网格划分
直接运用ICEM对二维喷嘴水射流流场建模并进行网格划分。采用结构化网格划分,因为结构化网格比非结构化网格更容易收敛,计算速度更快,也更准确。以d型喷嘴为例,网格划分后的结果如图1所示。

图1 d型喷嘴的网格划分
4.2 模型选择与边界条件确定
文中考虑的属于非淹没自由水射流,喷射出的水在空气中运动并与空气发生剧烈的能量传递和动量交换,因此采用气液两相流模型[8]。根据雷诺数求解公式Re=vdH/υ,可得水射流运动状态为湍流,因此采用标准的k-ε模型。
设置计算域边界条件,取d型喷嘴的射流流场计算域为例,如图2所示,其中边A设置为速度入口,将第二相水的体积分数设置为1,表示入口充满水;边B设置为自由出口;CDEC1D1E1设置为固体壁面,采用FLUENT中默认的无滑移条件,且对近壁处的流体应用近壁函数。二维水射流流场参数尺寸分别为:喷嘴入口长度为20 mm,喷嘴出口长度为10 mm,喷嘴入口速度为1 m/s。
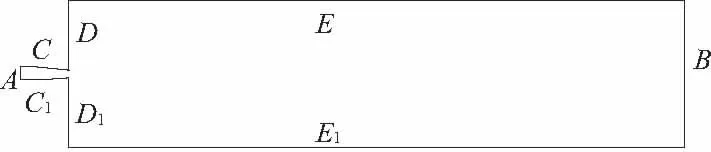
图2 二维喷嘴水射流流场
4.3 仿真结果及其分析
分别对上述4种喷嘴进行水射流流场仿真,结果如图3所示。
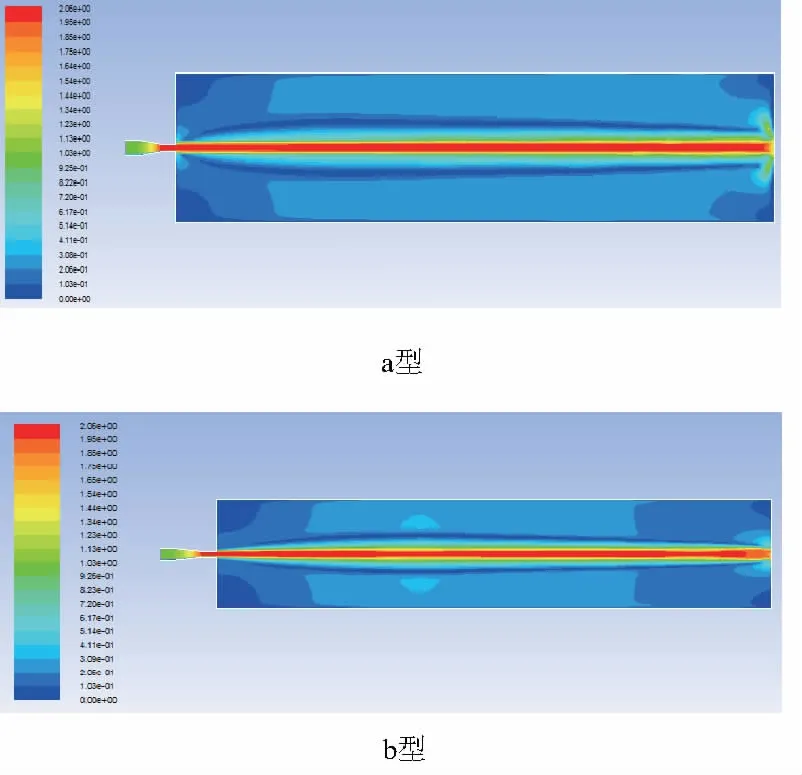
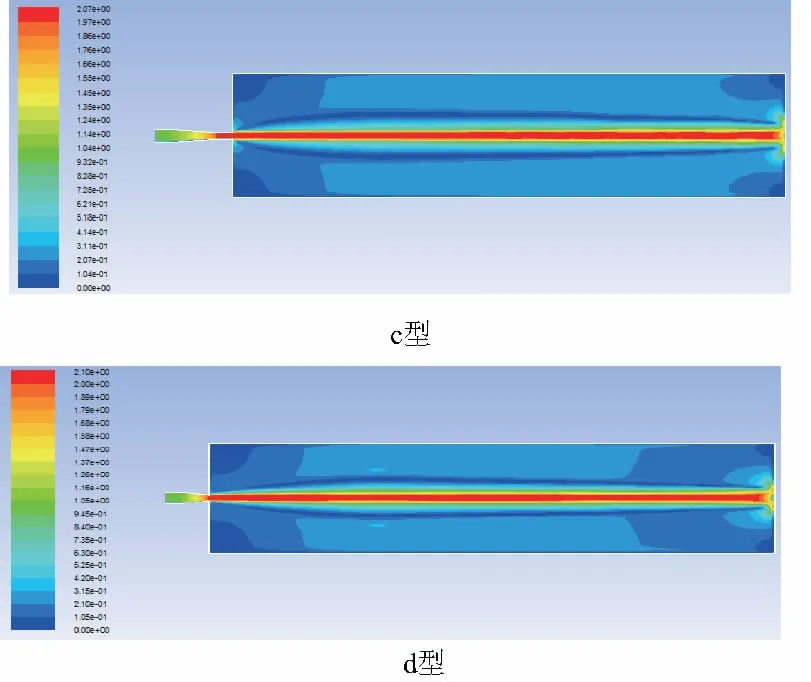
图3 喷嘴水射流流场速度云图
由图3可得水流从喷嘴中喷出后的速度均为2m/s左右,而根据连续性方程可知,喷嘴出口的速度为2m/s,仿真出的结果与理论公式求解出的结果近似相等。
当锥直形喷嘴的收缩角不同时,喷嘴出口速度和喷嘴出口静压会发生变化,其关系分别如图4和图5所示。
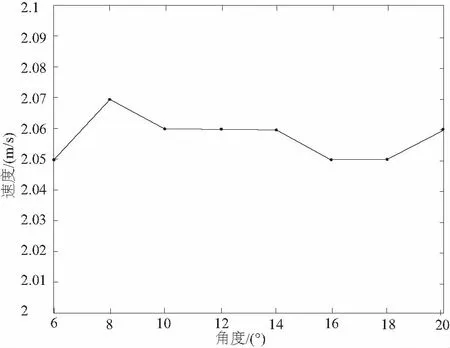
图4 喷嘴收缩角对喷嘴出口速度的影响
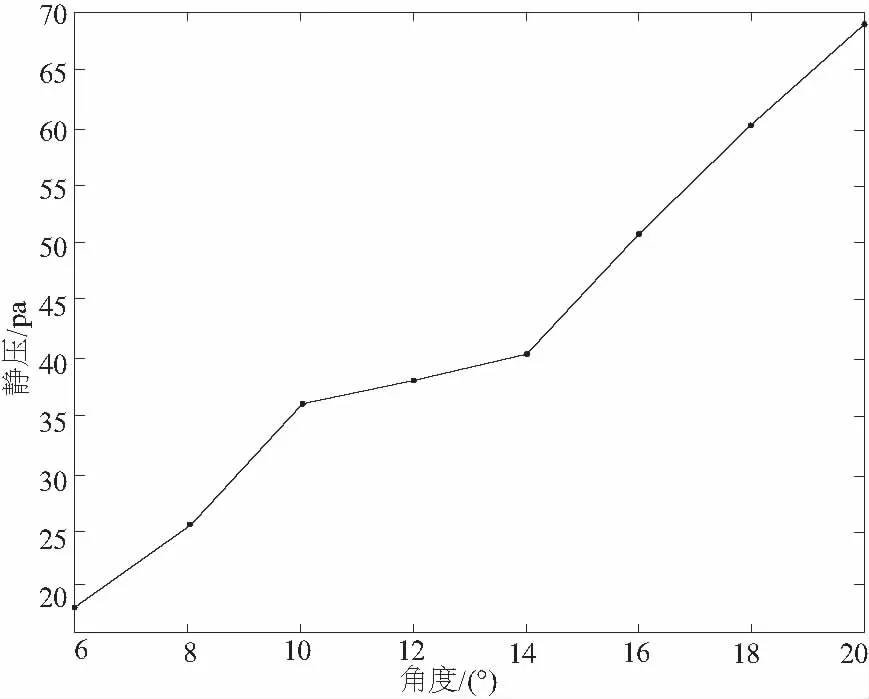
图5 喷嘴收缩角对喷嘴出口静压的影响
比较a型和b型喷嘴水射流流场的仿真结果可得:a型喷嘴内部流场相比b型的更紊乱;b型喷嘴整流段内的流体也比a型喷嘴的平缓。比较c型和b型喷嘴水射流流场的静压,发现收缩角为8°的喷嘴在出口处静压要小于收缩角为14°的喷嘴。这很好地证明了理论,即收缩角越小在收缩断面形成的阻力就越大,从而导致能量耗散的增加,根据能量守恒定律,流体能量的耗散主要体现在静压的变化上。综合考虑喷嘴出口速度与静压的影响,通过图4和图5得到:收缩角为14°的喷嘴对水射流性能提高更有利。
当锥直型喷嘴的长径比不同时,喷嘴出口速度不同,通过仿真得到其关系如图6所示。
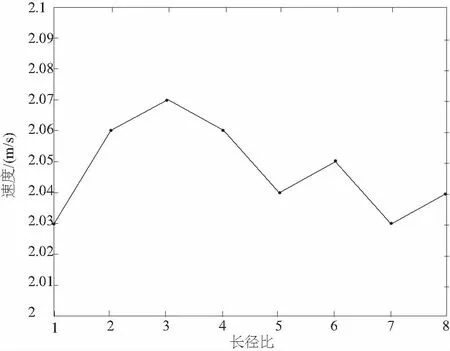
图6 喷嘴长径比对喷嘴出口速度的影响
比较b型和d型喷嘴形成的水射流流场,有整流段的喷嘴出口速度与没有整流段的大致相同,但从b型喷嘴中喷射出的水流更加平稳。经过大量仿真得到图6所示规律,则当长径比为2~4时,喷嘴出口的速度最大。在喷嘴直径变化处,由于水流流线不能够转折,射流会发生收缩,但射流在受到阻力后要发生扩散。当有适当长度的整流段时,扩散的射流就会发生附壁,在离开喷嘴前,液体已充满整个截面,即收缩断面发生在喷嘴的整流段内部,使喷嘴的截面收缩系数ε=1。同时收缩断面处存在一定的真空度,因此对于锥直型喷嘴形成的水射流,不仅有动压的驱动作用,而且还有真空抽吸作用,从而使出口流量有所增加,即具有整流段的喷嘴喷射出的水流流量一定大于没有整流段时的流量。但当收缩断面上的绝对压力低于当地的饱和蒸汽压力时,水流又将会在流过该截面处发生气化,应避免出现这种情况。
5 结语
1) 选用FLUENT中的vof模型和标准的k-ε模型对不同结构喷嘴进行水射流流场仿真,仿真出的结果与理论值相似。
2)不同喷嘴结构对水射流性能具有较大影响。对于锥直形喷嘴而言,当收缩角为14°且喷嘴长径比为2~4时,水射流性能最好。
[1] 魏德军,曹仲文,李萍. 喷嘴形状对喷射能力的影响[J]. 辽宁化工,2006,35(7):416-418.
[2] 薛胜雄. 高压水射流技术工程[M]. 合肥:合肥工业大学出版社,2006.
[3] 杨友胜,张建平,聂松林. 水射流喷嘴能量损失研究[J]. 机械工程学报,2013,49(2):139-144.
[4] 刘沛清. 自由紊动射流理论[M]. 北京:北京航空航天大学出版社,2007.
[5] 裴二荣,柴金城. 喷嘴水力性能分析及设计[J]. 排灌机械,2004,22(5):29-31.
[6] 孙德志,杨周,刘炜丽,等. 基于FLUENT的不同喷嘴轮廓线形对流出系数影响分析[J]. 理论与实验,2007(12):3-6.
[7] 王福军. 计算流体动力学分析—CFD软件原理与应用[M]. 北京:清华大学出版社,2005.
[8] 罗惕乾. 流体力学[M]. 北京:机械工业出版社,2007.
Analysis of Influence of Nozzle Convergence on Water-jet Capacity
LI Jun, ZHANG Qing,ZHOU Yizheng
(Nanjing University of Science and Technology, Nanjing 210094,China)
This paper introduces the theory of water-jet and mathematical model of its computational fluid dynamics and uses FLUENT solfware to simulate and analyae the water-jet flow fields with different nozzles. According to the compared result of the simulation,the rectifying section of nozzle not only has influences on the water-jet velocity, but also prompts the increase of the nozzle outlet flow. When the convergence angle of the nozzles is 14 degree, the performance of the water-jet is the best.
water jet; nozzle configuration; flow field simulation
李俊(1990-),男,江苏扬州人,硕士研究生,研究方向为机械设计。
TP391.9
B
1671-5276(2015)05-0102-03
2014-03-04
