精密光学元件表面中频误差的提取研究

林建兴，高诚辉，b，任志英,b

(福州大学 a. 机械工程及自动化学院，b. 摩擦学研究所，福建 福州 350002)

精密光学元件表面中频误差的提取研究

林建兴a，高诚辉a，b，任志英a,b

(福州大学 a. 机械工程及自动化学院，b. 摩擦学研究所，福建 福州 350002)

能否准确对精密光学元件表面评价势必影响着光学元件研制与生产，其中中频误差的提取逐渐显得重要。提出了利用双树复小波变换(DT-CWT)对精密光学元件表面提取信号进行多尺度分解，以定义的均方根波长确定其双树复小波分解次数，进行中频误差的提取与识别。此方法应用于精磨和镀膜的精密光学元件表面中，实验证实该方法不仅可以应用于一维信号的提取，同样也适合三维表面中频波段面形误差的提取。

双树复小波；精密光学元件表面；中频误差；提取

0 引言

随着光学技术的发展,光学元件在紫外线和X射线光学、超高反射率光学以及半导体工业中有着越来越广泛的应用[1]。由于需求量与应用领域的扩大，对光学元件表面品质和性能的要求更高，制造光学元件的面形误差(包括光学材料的不均匀性造成的误差和在光学加工过程的残余误差)对光束的调制作用会严重影响光束品质[2]。

传统评价光学元件表面的面形精度主要用PV值、均方根以及粗糙度等简单的统计参数来描述，但这些参数仅仅只包含光学元件表面的高频波段和低频波段的面形误差，对于中频波段的面形误差却没有做出相应的评价。然而中频波段的面形误差对光学性能产生很大影响，高志山[3]研究了中频波段波面误差对光学系统象质的影响，得出了中频波段波面误差引起光能小角散射，严重降低光学系统成象分辨率的结论。特别是在高功率激光装置中，中频误差的位相扰动随着波面的传输，会使激光束强度分布出现调制，导致光束的非线性增益，最后将严重影响激光束的聚焦，因此中频波段面形的评价可以完善表面品质的评价体系，对光学元件的研发与生产具有重要的意义。正确评价中频波段面形误差的首要条件是能否真实提取中频面形误差，徐建程等[4]尝试利用Wigner分布函数评价光学元件中频误差，识别局部小尺度波前畸变的空间频率和空间位置，能够有效指导光学元件返修，但局部小尺度并不能完全表征整个光学元件表面中频段误差。郭隐彪等[5]基于经验模态分解有效识别中频误差特征及其方位，但采用经验模态分解时对于采集信号的要求相对较高。

1998年，受到傅里叶变换的启发，Kingsbury[6]首次提出双树复小波变换(DT-CWT)。其滤波器应该要满足有限支撑、完全重构条件即正交或者双正交、近似的半帧移以及对称性等四个条件。双树复小波变换具有良好的局部化的分析能力以及良好的方向检索性能，已在图像去噪、图像纹理提取和图像加强等方面成功的应用[7-9]。由此说明双树复小波可以对复杂的信号进行特征信号分解以及提取。文中提出利用DT-CWT进行多尺度分解，并首次运用均方根波长确定双树复小波分解次数后，最后进行中频误差的提取与识别。将此方法应用于精磨和镀膜的精密光学元件表面中，证实该方法不仅仅可以应用于一维信号的提取，同样也适合三维表面中频波段面形误差的提取。

1 DT-CWT分离光学元件表面中频误差的建模

1.1 中频误差分离数学建模

目前光学元件的面形误差信号由低频分量扰动的面形误差信号，中频分量波纹度面形误差信号以及高频分量粗糙度的面形误差信号构成。所以采集光学元件表面面形误差信号f(xi)可建立以下数学模型：

f(xi)=s(xi)+z(xi)+r(xi)

(1)

式中：s(xi)为低频分量面形误差信号，z(xi)为中频分量面形误差信号，r(xi)为高频分量面形误差信号。

采用传统一维的光学元件表面轮廓信号进行参数评定时，评定参数中均方根波长考虑了区域内所有单峰和单谷的相对幅度和各自空间频率的间距量度，是横向间距特性参数，其基本公式为：

(2)

式中：Sq为长度均方根偏差，Sdq为长度均方根斜率值，其Sq和Sdq离散的公式如下：

(3)

(4)

从式(4)可知，Sdq长度均方根斜率值与波前梯度均方根(GRMS)相对等，然而波前梯度均方根是衡量波前低频相位畸变的重要标准，目前张颖等[10]推导出波前梯度均方根与焦斑尺寸存在定量的关系，间接反映均方根波长与光学特性密切相连。因此参考美国劳伦斯·利弗莫尔实验室在研制NIF过程中对空间波长的划分[11-12]对均方根波长进行面形误差的分组如表1。

表1 均方根波长面形误差分组

1.2 双树复小波分解基本过程

对于任何采集光学元件表面信号f(xi)，对其进行双树复小波变换中高频面形误差的提取基本流程如图1，具体步骤如下：

1) 将原始表面信号f(xi)进行双树复小波的n层分解，得到最底层的低频系数dn(xi)以及各层的高频系数cj(xi),j=1,2,...,n。

2) 对分解得到具有细节信号的高频系数cj(xi)进行重构得到：

(5)

3) 接着将具有细节信号的高频系数cj(xi)全部置零处理，并对低频系数进行信号的重构h2(xi)，记作：

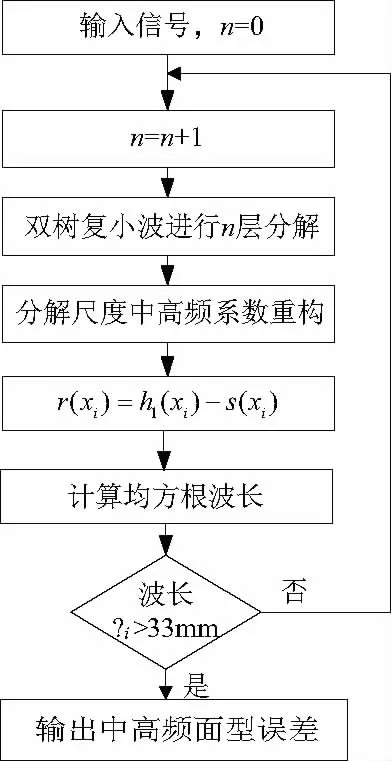
图1 双树复小波提取面形误差流程图

(6)

4)将原始表面信号f(xi)减去低频分量面形误差s(xi)，得到的信号进行均方根波长λi计算，如果λi<33mm重复上面的步骤，直到λi≥33mm结束循环。设定此循环次数为双树复小波的分解尺度，进行中高频面形误差的分离。中频面形误差为：

z(xi)=h2(xi)-s(xi)

(7)

高频面形误差为：

r(xi)=h1(xi)-s(xi)

(8)

2 仿真和实验分析

2.1 抛光光学球面一维数据仿真分析

光学球面常采用子午线来确定光学元件的面形,因为子午线影响着光学的焦斑、像散以及屈光度等性能，现文中选择对球面子午线进行双树复小波各尺度分解，计算各尺度下的均方根波长如表2所示。

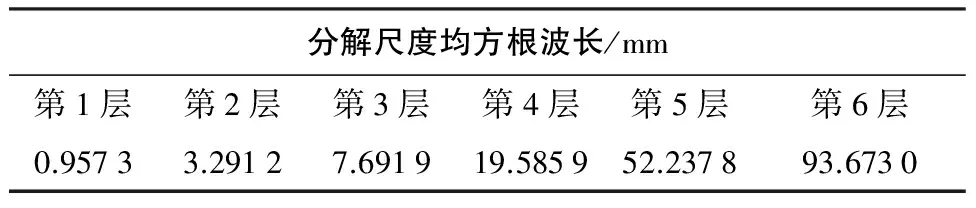
表2 球面分解各分解尺度均方根波长

由表2可知，当分解层数至第4层时，λi≤33mm，则确定双树复小波分解次数为4层。将前4层的低频信号进行重构得到中频面形误差以及高频信号进行重构得到高频面形误差，如图2所示。

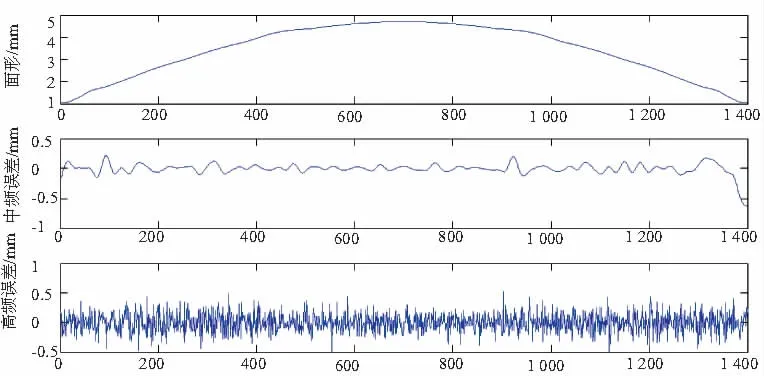
图2 光学球面子午线误差分离结果

由图可得出，经过抛光后光学元件表面的中频面形误差表面比较光滑，且波纹度具有一定的相似性，但在采样点1300～1400中存在较大的波动，因此需对后续抛光的工序进行一定修正；高频面形误差分布呈现无规律的分布，但其幅度相对较为对称，说明该抛光加工工况(抛光液、机床振动等)较为良好。

以上说明了双树复小波可以很好的将抛光光学元件表面一维中频波段的面形误差与高频波段进行分离，并且可以进行缺陷识别与定位。

2.2 实测镀膜光学元件表面三维数据分析

目前大量的国内外文献对于中频误差的提取只进行一维的实验。为了充分体现双树复小波不仅仅能够运用于一维的提取，而且可推广到光学元件表面三维数据中频误差的提取，现采用实际镀氟化镁膜的光学玻璃样品作为中频面形误差提取的研究对象，通过原子力显微镜对其进行扫描，得到表面的三维图见图3。

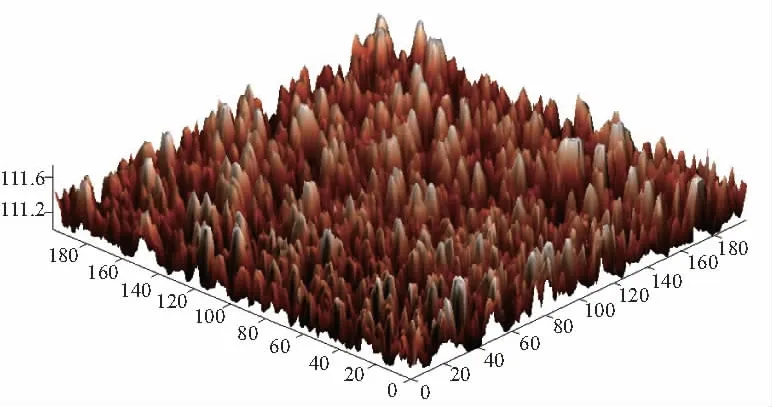
图3 基于AFM的光学镀膜元件表面样品图片三维图

运用双树复小波对其进行多尺度分解与均方根波长的计算，得到各尺度下的均方根波长如表3所示。

表3 镀膜三维表面各分解尺度均方根波长

同理，确定双树复小波分解次数为4层，并将前4层的低频信号进行重构得到中频面形误差以及高频信号进行重构得到高频面形误差，如图4、图5和图6所示。

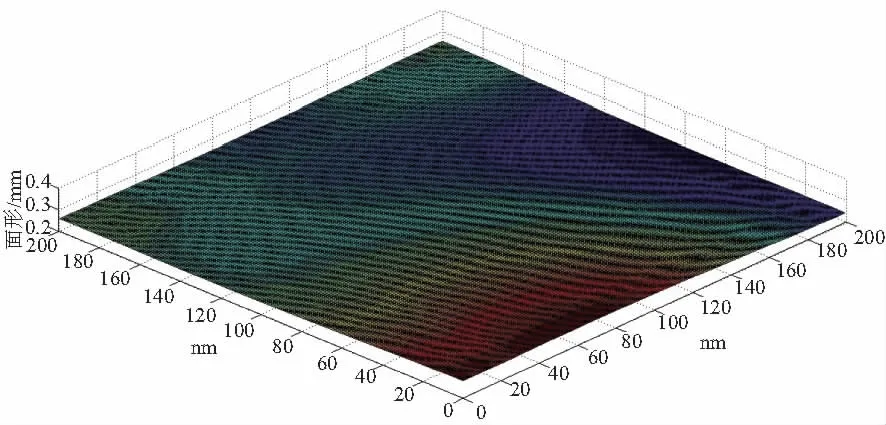
图4 面形三维图

图5 中频面形三维图

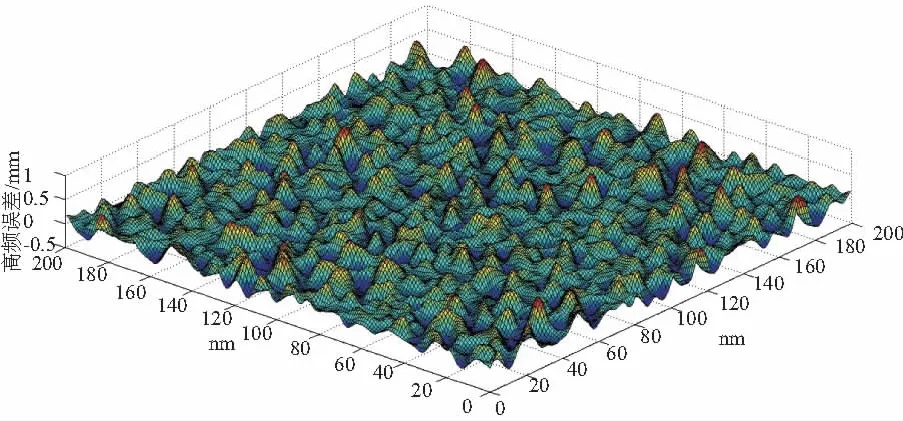
图6 高频面形三维图

由图5可得出，经过镀膜后三维光学元件表面的中频面形误差表面不够规整，局部个别地方较为凹陷与凸出，间接反映镀膜基底存在一定的缺陷；从图6高频面形误差三维图可看出其高频面形误差高度相互对称，反映了镀膜厚度较为均匀，说明该镀膜工艺较为良好。因此双树复小波可以较好分离镀膜的光学元件表面三维中高频面形误差。

3 结论

通过以上理论分析以及实例运用得出以下结论：

1) 运用双树复小波进行数据多尺度分解，提出通过计算各尺度下的均方根波长来确定双树复小波分解尺度，从而来提取光学元件表面的中频误差。

2) 运用双树复小波对抛光光学球面一维数据提取的中频面形误差效果较好，而且可以有效地识别加工工序存在的缺陷，为后续加工工序的改进提供优化的方向。

3) 对于三维光学元件表面中频误差提取，能够更加真实地反映实际加工所包含的空间信息，将双树复小波从一维光学中频误差的提取推广到三维光学元件表面中频误差的提取，得到实际三维中频误差表面。

[1] 沈正祥,王占山,马彬,等. 利用功率谱密度函数表征光学薄膜基底表面粗糙度[J]. 光学仪器，2006,28(4)：141-145.

[2] Yoshihaur.Nmaba，Ult Parereision grinding of optical materials for high power lasers[J]. SPIE，1998，(3244):320-330.

[3] 高志山. 光学表面轮郭功率谱密度对象质的影响及干涉测试研究[D]. 南京：南京理工大学，1999.

[4] 徐建程，李海波，范长江. 基于 Wigner 分布函数的光学元件评价方法[J]. 强激光与粒子束，2010，22(11)：2621-2624.

[5] 毕果，郭隐彪，杨峰. 基于经验模态分解的精密光学表面中频误差识别方法[J]. 机械工程学报，2013，49(1)：164-170.

[6]Selesnick IW, Baraniuk R G, Kingsbury N G.Hilbert transform pairs of wavelets bases [J]. IEEE Signal Process.Le tt.2001, 8(6):170-173.

[7] N G Kingsbury. The dual-tree complex wavelet transform: a new efficient tool for image restoration and enhancement, Proc.European Signal Processing Conference, EUSIPCO 98,Rhodes, 1998:319-322.

[8] J F A Magarey, N G Kingsbury. Motion estimation using a complex-valued wavelet transform,IEEE Trans.on Signal Processing, 1998,46(4):1069-84.

[9] N.Kingsbury.Image processing with complex wavelets, Phil. Tran. R.Soc. Lond. A, 1999, 357: 2543-2560.

[10] 黄晚睛，张颖，刘兰琴，等. 光学元件波前梯度均方根与焦斑尺寸的关系[J]. 光学学报，2012,32(F12)：200-213.

[11] SCHINHAERL M，RASCHER R，STAMP R. Utilization of time-variant influence functions on the computer controller polishing [J]. Precision Engineering，2008，32(1)：47-54.

[12] AIKENS D M， WOLFE C R， LAWSON J K. The use of power spectral density (PSD) functions in specifying optics for the national ignition facility [J]. Proceeding of SPIE，1995,(2576)：281-292.

Precision Optical Surface Intermediate Frequency Error Extraction Research

LIN Jianxinga，GAO Chenghuia,b, REN Zhiyinga,b

(a. Department of Mechanical Engineering;b. The tribology Institute, Fuzhou University, Fuzhou 350002，China)

The ability to evaluate the precision optical component surface accurately is bound to affect the development and production of optical components, more and more attention is paid to researching on the intermediate-frequency surface shape error. This paper uses the dual tree complex wavelet transform (DT - CWT) to proceed a multi-scale decomposition of a signal extracted from the precision optical component surface, applies the defined root-mean-square wavelength to determining the number of dual tree complex wavelet decomposition. It conduct the intermediate-frequency error extraction and recognition. This method is applied to fine-grinding and coating precision optical component surfaces, and the experiment proves this method not only can be applied to one dimensional signal extraction, but also suitable for the extraction of 3-D medium frequency band surface shape error.

dual tree complex wavelet; precision optical component surface; intermediate frequency error; extraction

国家自然科学基金资助项目(50775039 )；清华大学摩擦学国家重点实验室开放基金资助项目(SKLTKF13B02)；福建省教育厅A类资助项目(JA13059)

林建兴(1989-)，男，福建泉州人，硕士研究生，研究方向为光学镜片表征和信号处理。

TG58

B

1671-5276(2015)05-0085-04

2014-03-14