铁磁材料磁滞回线的BP神经网络分析方法设计

王蕴杰

(青海师范大学,青海西宁 810008)

铁磁材料磁滞回线的BP神经网络分析方法设计

王蕴杰

(青海师范大学,青海西宁 810008)

BP神经网络可以通过调整连接权重按预定精确度逼近非线性函数,利用这一特点可对非线性函数关系进行拟合。文章中利用BP神经网络对铁磁材料磁滞回线实验数据进行了拟合与处理,结果显示该方法处理结果精确度高,拟合效果好。

铁磁材料;磁滞回线;BP神经网络

磁滞回线是指在铁磁材料处于外磁场中时,铁磁材料内部的磁感应强度B与外部磁场强度H的关系可用曲线来表示,当外部磁场的磁场强度H作周期性的变化时,铁磁体中的磁感应强度B与外部磁场强度H的关系构成一条闭合线,这条闭合线便是磁滞回线。

1 铁磁材料的磁滞洄线

1.1 铁磁物质的磁滞现象

铁磁性物质的磁化过程一般都是通过测量外磁场的磁场强度H和铁磁材料的磁感应强度B之间的关系来研究其磁化规律的。

图1 铁磁材料的磁滞回线

当铁磁物质中不存在外部磁场时,H和B均应为零,在B-H图中则相当于坐标原点O(如图1所示)。随着外部磁场H的增加,B也随之增加,但两者之间不是线性关系。当H增加到一定值时,B不再增加(或增加十分缓慢),这说明该物质的磁化已达到饱和状。Hm和Bm分别为饱和时的磁场强度和磁感应强度(对应于图中的A点)。如果再使H逐步退到零,则与此同时B也同时减小。然而,其轨迹并不沿原曲线AO,而是沿着另一曲线AR下降,这说明当H下降为零时铁磁物质中仍保留一定的磁性。将磁化场反向,再逐渐增加其强度,直到H=-Hm这时曲线达到A′(即反向饱和点)。然而,先使磁化场退回到H=0;再使正向磁化场逐渐增大,直到饱和值Hm为止。如此就得到一条与ARA′,对称的曲线A′R′A,而且自A点出发又回到A点轨迹为一闭曲线,称为铁磁物质的磁滞回线,在此属于饱和磁滞回线。其中回线和H轴的交点Hr和H′r,称为矫顽力,回线与B轴的交点Br和B′r,称为剩磁[1]。

1.2 磁滞回线的测量

实验采用的测量方法是在待测的铁磁材料样品上绕上一组磁化线圈,外部磁场强度可以用下式来表示,其中N为线圈匝数、I为励磁电流,L为平均磁路长度。

在环形铁磁材料样品的磁路中开一极窄均匀气隙。在磁化线圈最大值磁化电流磁锻炼基础上,用特斯拉计测量气隙均匀磁场区中间部位的磁感应强度B,即能得到该磁性材料的磁滞回线。

2 铁磁材料磁滞回线测量的数据处理

2.1 测量数据

按照上述的方法,利用HM-1型磁滞回线测试仪对Cr-12模具钢的磁滞回线进行测量,数据如表1所示:

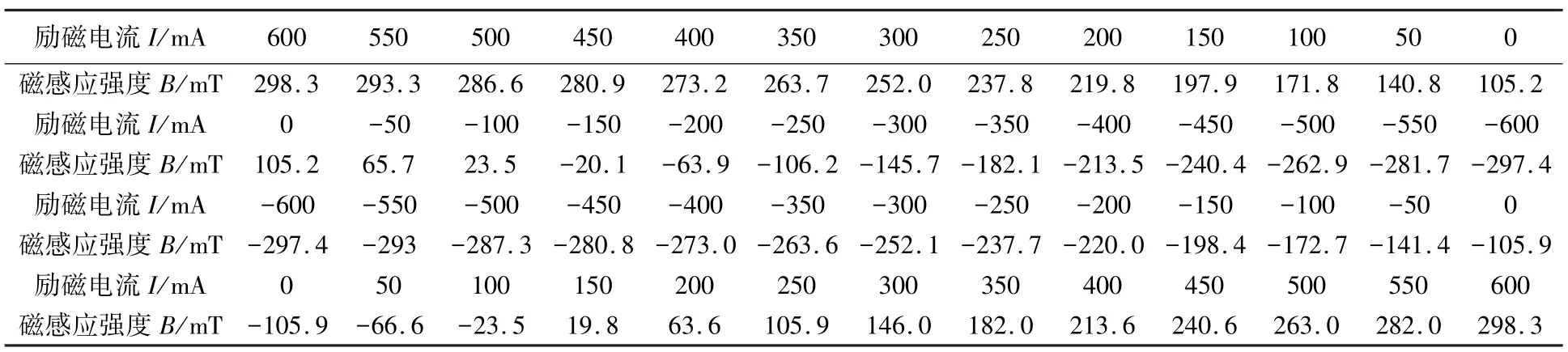
表1 磁滞回线测量数据

2.2 BP神经网络对测量数据的处理

如图2所示,BP神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络之一。BP网络学习规则采用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层、隐层和输出层。BP神经网络通过调整连接权重便可按预定精确度逼近非线性函数,利用这一特点可对非线性函数关系进行拟合[2]。

图2 BP神经网络

BP(Back Propagation)算法本质上是利用实际输出与期望输出之间的误差,对网络的各层连接权值和各结点的阈值由后向前逐层进行调整的一种有监督的学习算法。BP算法根据最小二乘原理和梯度搜索技术,将学习过程分为输入样本信息的正向传播和误差的反向传播两个过程。输入样本从输入层传递给隐藏层各结点,经过各隐藏层用传递函数逐层处理后传递给输出层,若输出层的实际输出与期望输出的误差达不到预定的要求,则转入误差的反向传播过程,即将误差沿原来的连接通路返回,通过调整各层的连接权值及阈值,使实际输出与期望输出的误差逐渐减小。这种输入样本正向传播与误差反向传播的过程反复进行,直到误差达到预定的要求为止[3-4]。

利用Matlab的神经网络工具箱设计BP神经网络,该神经网络输入层、输出层神经元采用线性传输函数(purelin),神经网络含有一层隐含层(含20个神经元),隐含层的神经元采用S型激活函数(双曲正切函数 tansig),程序在 Matlab 2013b环境运行通过。其主要的程序段如下:

在处理程序中,为了加快神经网络的收敛速度,训练前对输入、输出样本进行了归一化处理,利用BP神经网络对磁滞回线进行了分段的拟合,分别对图1中的ARA′及对称曲线A′R′A设置训练参数(lr=0.03、goal=1.0×10-11与lr=0.5、goal=7.5×10-12)。运行程序,如图3~4所示,曲线各经训练161、74次后,神经网络误差平方和达到了数据处理预先所要求的训练目标goal值以内,可见其训练过程是收敛的。对神经网络的仿真值进行还原后,可作出铁磁材料磁滞回线如图5所示。

图3 ARA′曲线BP神经网络训练收敛曲线

图4 A′R′A曲线BP神经网络训练收敛曲线

图5 磁滞回线

2.3 矫顽力、剩磁的确定

由铁磁学知识可知:磁滞回线上外磁场H为0处是该材料对应的剩磁Br、B′r;回线上B为0处为该材料的矫顽力Hr、Hr′[5-7]。依据上述原理,设计处理程序在Matlab 2013b环境运行通过,主要程序段如下:

利用上述程序对表1数据进行处理,得到的矫顽力相对应电流分别为127.2 mA和-127.04 mA,通过实际测量可以得出其矫顽力对应励磁电流分别为127.6mA与-126.8mA,可见其符合程度是相当高的。其运行结果如图6所示。

图6 处理程序运行结果

3 结 论

文章中利用BP神经网络对铁磁材料磁滞回线数据进行了处理,可以看出利用BP神经网络对非线性数据拟合精度是比较高的,并可以方便的利用训练收敛后的BP神经网络求得未测量点的数据值,并进行处理。文章中所给出的用BP神经网络处理铁磁材料磁滞洄线数据的方法,不仅能根据建立的数学模型计算出材料的特征参量,而且可以精确绘制出材料的磁滞洄线图像,并与实际的测具有很好的符合度。

[1] 戴道生.铁磁学[M].北京:科学出版社,1998.

[2] 李国勇.智能控制及其MATLAB实现[M].2版.电子工业出版社,2005.

[3] 朱大奇.人工神经网络原理及应用[M].北京:科学出版社,2006.

[4] 王蕴杰.铁磁材料居里温度测量的BP神经网络分析[J].微型电脑应用,2014,30(5):32-34.

[5] 王蕴杰.铁磁材料磁滞洄线的Matlab分析方法设计[J].电脑开发与应用,2012,25(7):51-53.

[6] 魏奶萍,张相武,朱君凡.Mathematic软件在铁磁材料磁滞目线中的应用[J].大学物理实验,2014(6): 96-99.

[7] 王连加.多项式拟合铁磁材料的磁滞目线曲线[J].大学物理实验,2006(3):58-61.

Analysis of Ferromagnetic M aterials Hysteresis Loop by BP Neural Network

WANG Yun-jie
(Qinghai Normal University,Qinghai Xining 810008)

It uses BP neural network to process the data in ferromagnetic materials hysteresis loop.The result shows thismethod has the high precision of processing result,good effect of fitting.

ferromagneticmaterials;hysteresis loop;BP neural network

O 4-39

A

10.14139/j.cnki.cn22-1228.2015.006.002

1007-2934(2015)06-0004-04

2015-07-03

青海师范大学2014校级科研项目资助