高考中一道“裂项求和”问题课本探源
2015-07-01广东省兴宁市第一中学赖海波
☉广东省兴宁市第一中学 赖海波
高考中一道“裂项求和”问题课本探源
☉广东省兴宁市第一中学 赖海波
“裂项求和法”是数列求和问题中重要的一种方法,多次出现在全国各省市的高考命题中,其本质是“裂项相消”,即把数列的每一项裂分成两项之差求和,正负相消之后剩下首尾若干项.本文以2014年高考山东卷中数列解答题为例,就裂项法在数列求和中的应用进行探究.
题目(2014年山东卷)已知等差数列{an}的公差为2,前n项和为Sn,且S1,S2,S4成等比数列.
(1)求数列{an}的通项公式;
由题意得(2a1+2)2=a1(4a1+12),解得a1=1,所以an= 2n-1.
所以Tn=
例1(2012年高考全国)已知等差数列{an}的前n项和为Sn,a5=5,S5=15,则数列的前100项和为().
解析:设数列{an}的公差为d.
a5=a1+4d=5,S5=5,解得a1=1,d=1,则an=
S100=
变式1:根式型
例2已知数列{an}满足N*),则数列{an}的前n项和Sn=____________.
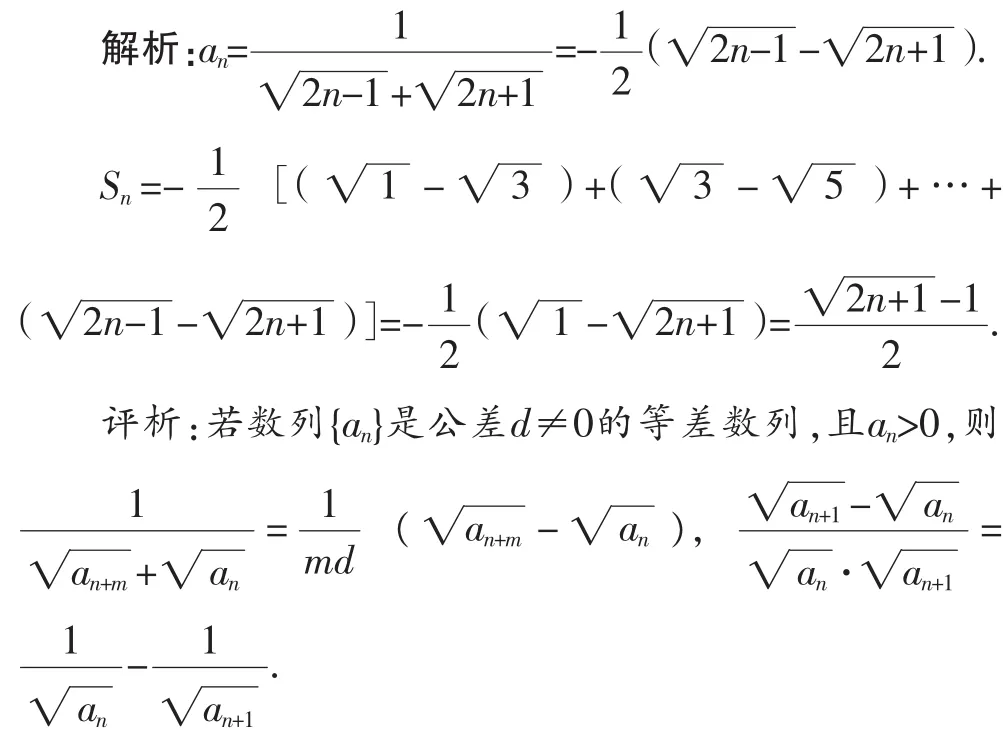
变式2:对数型
例3已知数列{an}满足则数列{an} 的前n项和Sn=______________.
Sn=(ln2-ln1)+(ln3-ln2)+…+[ln(n+1)-lnn]=ln(n+ 1)-ln1=ln(n+1).
变式3:指数型
例4已知数列{an}的前n项和为Sn,a1=3,数列{Sn+1}是公比为4的等比数列.
(1)求数列{an}的通项公式an;
解析:(1)Sn+1=(S1+1)·4n-1=4n,则Sn=4n-1.
当n≥2时,an=Sn-Sn-1=3·4n-1.又a1=3满足an=3·4n-1,故数列{an}的通项公式为an=3·4n-1.
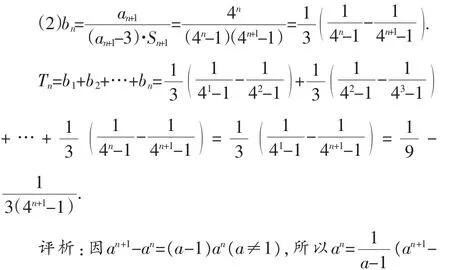
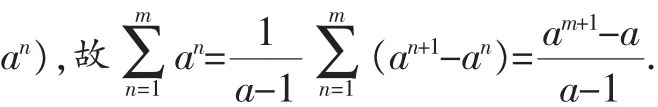
变式4:放缩后裂项
例5(2013年高考广东)设数列{an}的前n项和为Sn.
(1)求a2的值;
(2)求数列{an}的通项公式;

总之,裂项相消法是数列求和中应用最广泛的一种方法,一些常见数列(包括等差和等比数列),都可以采用裂项相消法求和.对于不能直接裂项求和的数列,则可通过放缩变形,使其成为可裂项求和类型.
