复杂信息化装备故障分析对比研究
2015-07-01陈小虎杨翊方
任 鑫,陈小虎,杨翊方,张 凯
(1.国防大学 a.研究生院; b.军事后勤与科技装备教研部,北京 100091;2.海军医学研究所,上海 200433)
伴随社会快速发展和战争形态的转变,以信息化为代表的高新技术不断涌现,使得装备信息化程度不断提高,体系构成也越来越复杂,装备故障分析对象多元且难度加大,导致采用传统的故障分析手段或模型有时已不能有效满足现实需要[1]。这就要求创新或改进已有的传统手段或方法,更加准确地分析复杂信息化装备故障,提高装备维修和保障效能,为打赢信息化条件下局部战争提供保证。本研究进行复杂装备2 种故障分析方法对比研究,首先将传统故障分析模型与改进模型进行理论上比较,然后进行实例分析,探讨依托传统方法进行改进后在现代装备故障分析的应用可行性。
1 传统分析模型及改进模型之理论对比
综合信息化装备非常复杂,一般由若干个子系统构成,并且各子系统结构和相应功能各不相同,通过局域网相连构成体系,其综合化和一体化性质使得复杂信息化装备功能强大,作战能力或保障效能通常远远高于一般装备,但复杂装备尤其是信息化高技术装备由于构成要素和链接点众多,不可避免地存在某种程度上的“一损俱损”或“牵一发而动全身”体系脆弱性[2-5]。为打赢未来信息化条件下的高技术战争,充分发挥信息化装备效能,对战损或故障的复杂装备或子系统进行准备的故障预测或分析就显得十分必要,有力保障装备的持续稳定性能。本文选择以下故障分析模型,并首先将传统和改进后模型在理论上进行对比分析。
1)传统灰色关联分析模型。信息化多数复杂装备系统为灰色系统,根据其故障和征兆之间通常并无确定的映射关系,故一般采用灰色关联模型进行故障分析[6],以故障和征兆两者之间发展趋势的异同来分析判断两者之间关系的故障。分析复杂系统内部各因子之间的关联系数及关联度,并通过后者大小来有效确定对故障影响大小的主次因素,此种分析方法对样本量要求不是十分苛刻,一般不需要样本服从某种分布规律,且只需要较少的计算量即可获得分析结果。建立传统一般灰色关联模型,首先需设定如下的状态数据为参考序列为X0=[x0(1),x0(2),…,x0(n)],设定如下标准故障样本集作为分析比较序列为Xi=[x1(1),x1(2),…,xi(n)](i=1,2,…,m),并设定εik为各参考序列与比较序列的灰色关联系数,用来表示各个时间段内各比较序列与参考序列的相吻合的程度。εik定义如下

式中:ρ∈(0,1)为分辨系数,为了计算方便,在一般灰色关联模型分析中常取0.5;εik为k 点的灰色关联系数;γi为参考序列和比较序列之间的对应元素的灰色关联度,计算时传统灰色关联分析中取各点出灰色关联系的算术平均值。
2)优化改进后分析模型。由于系统在运行的过程当中会受到多种不确定性因素的扰动,并且参考序列和比较系列在每个计算点的关联系数对整个灰色关联度计算时的影响是各异的[7],根据传统的灰色关联模型通常均将各个点的灰关联系数进行简单算术平均后就作为计算灰色关联度的取值,往往不能准确地反映系统参考序列和比较序列之间的关系,有时会因此产生信息损失而导致无法充分考虑系统特征波动对结果的影响和基于不同时点关联系数对复杂系统重要性的不同反映,产生复杂装备系统故障分析时其结果与系统本身现实情况严重不符,即系统故障诊断分析精确性较低的现象[8]。所以需要对传统的灰色关联分析模型进行优化改进,在计算参考序列和比较序列之间的灰色关联度时,采用添加权重的灰色关联度理论计算模型。主要在以下3 个方面对传统的模型进行优化为
第一步:首先改进通过计算各序列在各点关联系数平均值的方法,在传统关联度计算模型基础上引入权重并重新定义为

式中:εik(X0,Xi)为X0与Xi加权灰色关联度;wk为第k 点的权重,其值反映了各点对整体灰色关联度的影响,且满足
第二步:由式(3)可以看出,计算改进后加权灰色关联度数值,首先需要确定权重值wk。在利用灰色关联度模型进行故障分析时,灰色系统中比较序列对参考序列的影响应该维持稳定,并且这种影响期望是均衡客观的[9],所以本文采用熵权法来对引入权重进行赋值,通过建立相应拉格朗日函数并进行矩阵行列式运算,最终计算得出在最大化约束条件下的权重向量如下

第三步:在式(1)中分辨系数ρ 在传统灰色关联模型中取固定值0.5 降低了模型的抗干扰性,为了增加计算模型反映系统关联性的灵活性和真实程度,对分辨系数ρ 进行优化,采取根据系统参考序列和比较序列的具体情况进行动态调节取值,提高系统分辨能力。ρ 的动态取值如下

以上对传统灰色关联度模型进行改进后,可计算加权灰色关联度值,并对其进行大小排序,系统中关联度最大值对应故障则被认为诊断故障,从而完成复杂装备的故障分析。
2 传统模型和改进模型应用案例对比分析
1)故障分析系统的建立。复杂信息化装备系统集成,多功能一体,各部件故障机理复杂、种类多样且相互之间依存度大,进行精确故障诊断分析时需尽可能多地获取更多变量,无形中导致系统分析的不确定性增大,增加了“误诊”风险[10],所以为促进装备故障快速精准的分析,提高装备系统的可维修性和保障性,必须要建立适应复杂信息化装备系统故障特征的故障诊断系统,为操纵者提供及时准确的监测变量和可靠信息。下面本文根据上文优化改进模型建立复杂信息化装备系统故障分析系统,其结构如图1 所示。

图1 故障分析结构框图
由图1 可以看出此故障诊断系统主要由4 个部分组成,且之间利用串口通信协议进行完成各部分之间的数据传输任务[11],第一阶段部分获取被分析系统的运行参数;第二阶段部分主要对获取的数据进行科学预先处理;第三阶段部分引入改进优化加权关联度分析模型进行计算;第四阶段部分主要是分析得出系统故障诊断结果等。
2)实例分析。现在以某复杂信息化装备系统为例,基于优化改进灰色关联度模型来分析此装备系统,实现方法如下,以此装备系统状态表征参数为基础建立标准状态模式向量,并将各待测状态模式向量与此之间的关联度进行比较进而判断其所处状态,最终分析出此装备故障模式。首先建立某装备系统状态模式向量为
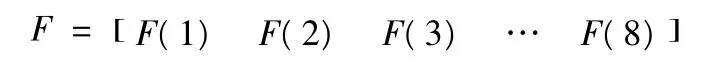
系统有8 个征兆集,其中F1,F2,F3,F4,F5代表5 种故障模式。


在故障诊断分析过程中,将采集到的系统状态数据:0.5,0.75,0.25,0.75,0.5,0.5,0.5,0.5,计算得到改进灰色关联度数据分别为ε(x0,x1)=0. 727 3,ε(x0,x2)=0.571 4,ε(x0,x3)=0.989 9,ε(x0,x4)=0.666 7,ε(x0,x5)=0.615 4,通过计算结果可以看出,x0,x3的加权关联度值最大,并且故障F3对应征兆集与采集系统状态数据相同,由此判断系统故障为F3。另外,关联系数和权重计算结果见表1所示。

表1 关联系数与权重向量
1)2 种模型系统敏感性对比分析
对复杂装备系统进行故障分析时,不可避免地会产生测量噪声,为了对比传统模型和改进优化灰色关联度模型参数和变量的改变对分析结果的影响,即分析结果对测量噪声的敏感性以测量系统稳定性程度。分别基于传统分析模型和改进优化模型对系统添加5%、10%的噪声,敏感性分析结果如图2 和3 所示。
由图2、图3 可以看出,2 种模型中系统均对第二和第四个征兆状态参数的敏感度最高,敏感性指数伴随噪声的增加而提高,而且传统模型敏感性数值比改进优化灰色关联度模型变化较快,所以改进模型对系统测量噪声的敏感度较低,即抗噪声干扰性能更强,具有较好的自稳自调性,更能真实地反映系统故障所在。

图2 传统模型添加5%、10%、15%噪声时系统敏感性分析

图3 改进优化模型添加5%、10%、15%噪声时系统敏感性分析
2)2 种模型系统分辨率对比分析
为了验证系统对故障的分辨能力,离线输入此状态数据:0.50、0.75、0.50、0.25、0.75、0.25、0.45、0.5,分别利用传统和改进优化灰色关联模型对此复杂装备系统进行故障分析。将2 种模型计算得到的关联度进行了归一化处理,得出如图4 所示关联度散点连线图,总体上2 种模型系统的故障关联度排序基本一致,因基于改进优化加权关联度模型2 种故障之间相距更远,改进优化模型具有更高的分辨能力。
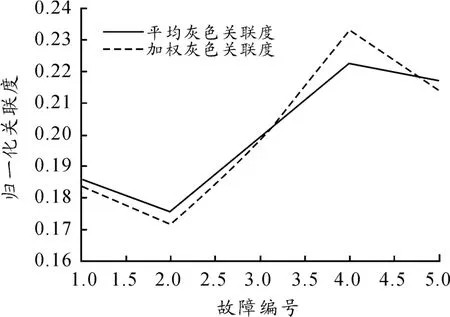
图4 2 种模型散点连线图的比较
另外,对传统和改进的灰色关联模型对故障的分辨率进行定量计算,得到各个故障模式之间分辨率,见表2 所示。可以看出改进优化模型系统分辨率均大于等于传统模型系统分辨率,改进模型对各种系统故障的区分度更大,故障诊断可靠性更高,故障分析结果更加准确可信。
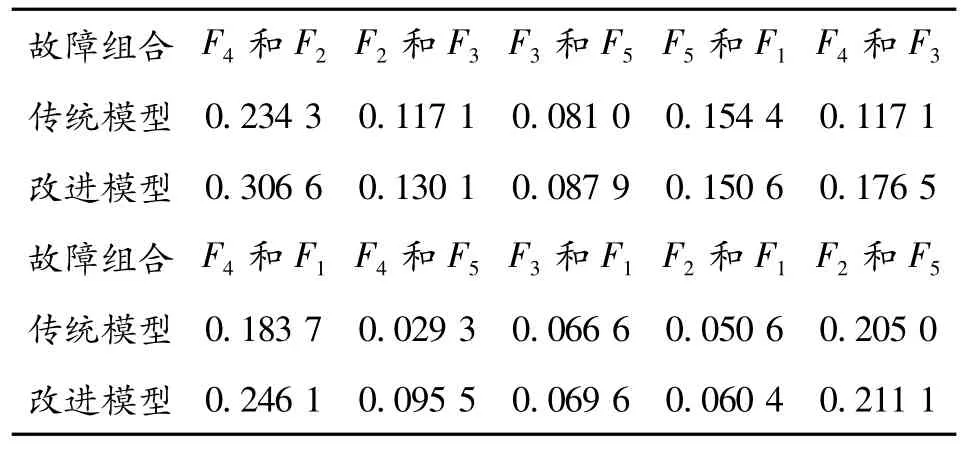
表2 2 种模型的故障分辨率比较
3 结束语
现代信息和网络技术在军事领域的广泛使用,信息化装备建设的步伐日益加快,其在信息化局部战争中将发挥越来越重要的作用,而由于信息化装备起步相对,投入使用时间也相对较短,故障样本数据较少,对其故障分析时可采用灰色关联模型进行分析,克服样本容量不足问题。但传统模型存在很多局限性,将传统模型和改进优化模型在理论对比分析的基础上,通过案例得出改进模型具有较好的稳定性和分辨率,获得了很好的使用效果,可有效应用于复杂信息化装备系统的故障分析。
[1]张炜,梁魏.复杂电磁环境下装备保障对策研究[J].装备指挥技术学院学报,2008,19(4):1-4.
[2]战晓苏.信息化战争与武器装备信息化的若干问题探讨[J].国防技术基础,2010(12):44-47.
[3]贾秀权,李鑫,胡斌.大型复杂信息化装备军民一体化保障的研究[J].现代电子技术,2013,36(11):25-27.
[4]李阳,武昌,雷志雄.装备维修保障信息化建设的若干问题[J].四川兵工学报,2013(4):113-115.
[5]李世英,曲长征,薛文力.信息化装备体系的RMS 参数体系框架研究[J].2008,22(6):39-42.
[6]周宇阳,陈汉平,王炜哲,等. 故障诊断灰色数学模型[J].中国电机工程学报,2002(6):146-151.
[7]MARKS R J. Intelligence:Computaional versus artificial[J]. IEEE Trans on Neural Networks,1993,4(5):737-739.
[8]徐小涛,田铖,朱学维.IETM 在信息化装备保障中的应用研究[J].国防技术基础,2008(9):22-29.
[9]程晋,严承华,樊攀星.基于CBR 的信息化装备故障案例推理复用技术研究[J].计算机与数字工程,2013,41(8):1308-1311.
[10]Friend A D,Scuhgart H H,Running S W. A physiologybased gap model offorest dynamics[J]. Ecology,1993,74(3):792-797.
[11]Daisuke Y,Li G D,Kozo M. On the generalization of grey relation-al analysis[J]. Journal of Grey System,2006,9(1):23-34.
