高速履带车辆悬挂装置仿真与耗能分析
2015-07-01于魁龙贾小平樊石光
于魁龙,贾小平,李 炯,樊石光
(装甲兵工程学院机械工程系,北京 100072)
传统的装甲车辆采用被动悬挂:一方面悬挂刚度和阻尼系数不可调,只能设计在特定工况下使其减振特性较好,很难适应不同道路及车速工况;另一方面阻尼元件以摩擦的形式将振动的机械能转化为热能耗散掉,从车辆减振器的使用寿命就可以看出,减振器承受较大的热负荷。另外随着履带式装甲车辆技术的发展,悬挂系统成为制约车辆越野速度提高的瓶颈。馈能型主动悬挂[1]在对振动能量回收的同时,通过对作动器参数的实时或是分级调节可以改变悬挂阻尼特性以适应不同工况,具有较大的应用价值。为此,首先对悬挂阻尼耗能功率进行分析。
1 联合仿真模型建立
1.1 履带车模型
本文基于RecurDyn 的高速履带专用工具包Trank -HM建立了图1 参数化的履带车模型[2-4]。模型包括车体子系统及两侧履带子系统;单侧履带子系统又包括:负重轮、平衡肘、张紧装置、诱导轮、托带轮、主动轮和履带板。

图1 履带车虚拟样机模型
根据履带车辆弹性元件和阻尼元件的工作特性,分别将其简化为线性扭转弹簧和扭转减振器[3],并设各负重轮扭杆刚度相同,在第1,6 负重轮处添加扭转减振器。第2,3,4,5负重轮没有添加减振器,但考虑各旋转副间的摩擦作用,在各旋转副上添加一定的阻尼,这样还能改善仿真的数值稳定性。
扭转刚度及扭转阻尼系数采用等效线性法[5]设定。由图2 可知,负重轮垂向位移h 与平衡肘转角α 的关系为
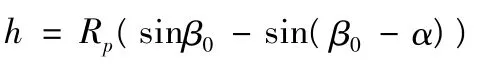
其中:Rp为平衡肘长度;β0为平衡肘静倾角;αj为静扭角。

图2 悬挂结构示意图
由扭杆和扭转减振器在垂向产生的力Fk、Fc分别为:

其中:KT,CT分别为扭杆刚度和扭转减振器阻尼系数;dh/dt 为垂向速度。且有

以上Fk,Fc均可利用Recurdyn 拟合成关于h 的幂级数形式,方便后面求解。
下面根据等效线性化方法设定KT,CT。先选择垂向刚度和阻尼系数Ke,Ce,垂向线性振动方程为
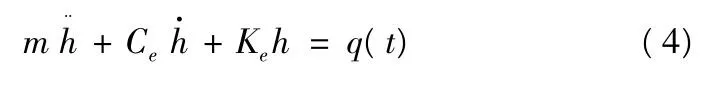
根据车辆垂向振动固有频率和相对阻尼系数计算垂向刚度和阻尼系数Ke,Ce选取车辆典型行驶路面不平度系数Gq(n0)及车速u,得到路面的功率谱密度,通过计算悬挂动挠度的方差及垂向加速度的方差Ke,Ce进行优化。

用等效线性化方法根据垂向刚度和阻尼系数Ke,Ce计算扭杆刚度和扭转减振器阻尼系数KT,CT。
车辆的非线性振动方程为


通常在进行非线性振动的等效线性化分析时,根据将已经确定的固有刚度阻尼进行线性化求出Ke,Ce再进行分析。具体方法是选择Ke,Ce使e(x,x)的均方值最小。同时,可以根据上述得到的方程先确定Ke,Ce,再设定系统的刚度阻尼。

也即



由此可求得:

结合式(1)、式(2)、式(3)、式(5)和式(6)求得扭杆刚度和扭转阻尼系数KT,CT。
1.2 发动机模型
在Matlab/Simulink 中建立了履带车的发动机模型,用以提供履带车模型的驱动。其中:目标车速模块根据仿真需要设定履带车模型的车速变化过程,为减少初始计算时长,本例中设为定值,同时在RecurDyn 中对所有惯性部件设定相应初速度;节气门子模块简化为二阶环节和滞后环节的串联模块,节气门开度采用PID 控制器; 发动机扭矩通过节气门和转速二维表获得;逆变速箱模块则根据车速求出挡位和发动机转速;履带车多体动力学模块通过ReucurDyn 建立Recurdyn_sub 子函数文件来表示。
运用Recurdyn/Control 接口技术[2]将整车多体动力学模型和基于Matlab/Sim-Link 的发动机扭矩控制系统模型结合,进行联合仿真,模型如图3 所示。在RecurDyn/Control 里定义输入变量两侧主动轮驱动扭矩torque1、torque2,输出变量车速velocity,同时设定执行的M 文件和仿真参数,最后在Matlab/Simulink 中运行求解。

图3 联合仿真模型
2 路面模型构造
本文采用随机路面作为验证悬挂性能的外部输入,随机路面的时域模型有:谐波叠加法(三角级数叠加法)、线性滤波法(伪白噪声法)、基于频率功率谱采样的数值模拟方法(傅里叶逆变换法)、时间序列分析模型法(AR 法、ARMA法)、分形分析模型法和小波分析模型法等[2,6],考虑到仿真时间等因素采用谐波叠加法。
根据ISO 标准,路面功率谱密度Gq(n)与参照路面的关系为

式中:n 为空间频率(m-1);Gq(n0)为参考空间频率n0下的路面不平度系数;w 为频率指数,决定路面功率谱密度的结构。选取有限个离散空间频率ni的三角级数来拟合随车辆纵向变化的路面不平度,以E 级路面为例,选择其路面激励曲线如图4 所示。
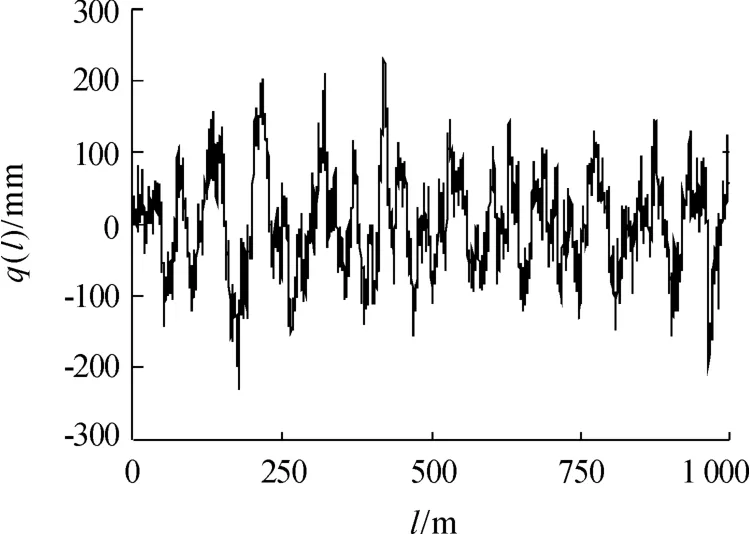
图4 E 级路面仿真模型的路面激励
按照RecurDyn 中路面节点单元生成的规则在Matlab 中构造基于三角形单元的二维随机路面,分别生成了D、E、F级随机路面。为简化计算选择坚实地面,取路面静摩擦因数u0=0.8,动摩擦摩擦因数u1=0.73。
3 模型仿真
分别对履带车辆车速为20 km/h、40 km/h 以及路面等级为D、E、F 的工况进行计算,其结果如图5 ~图8 所示。

图5 F 级路面40 km/h 车体质心加速度(1/g)

图6 E 级路面40 km/h 车体质心加速度功率谱
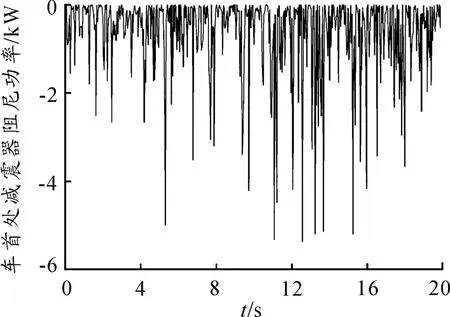
图7 D 级路面20 km/h 车首处减振器阻尼功率
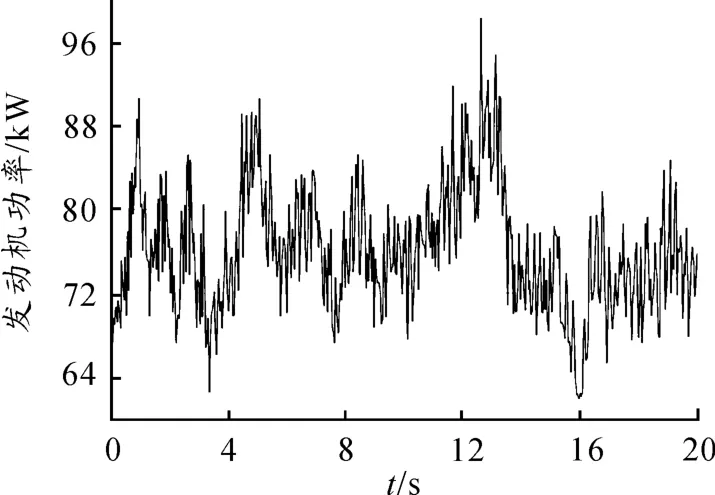
图8 E 级路面40 km/h 单侧履带发动机输出功率
从图5、图6 看出车体质心加速度峰值约为1.5 g(其中g 为重力加速度); 车体质心加速度功率谱曲线中峰值对应的频率为1.6 Hz,应该为车体质心垂直振动的固有频率,表明所建模型能够反映车辆行驶状态。
从图7 可以看出减振器阻尼功率的波动较大,以E 级路面车速为20 km/h 工况为例,虽然减振器阻尼功率峰值接近60 kW,但其平均值只有1.9 kW,给实际回收带来很大困难。
图8 为E 级路面40 km/h 时单侧履带发动机输出功率(计算到主动轮处所需的平均驱动功率)曲线,可以看出随路面不平度变化其波动较大。表1 中,减振器阻尼功率分别为单侧第1、6 减振器阻尼功率的平均值。作为外部激励中的2个重要因素,提高车速和增大路面不平度系数均会使所需发动机功率和减振器消耗的阻尼功率增加,但车速对阻尼功率占比影响很小,路面不平度系数对阻尼功率所占发动机所需功率的百分比影响很大。
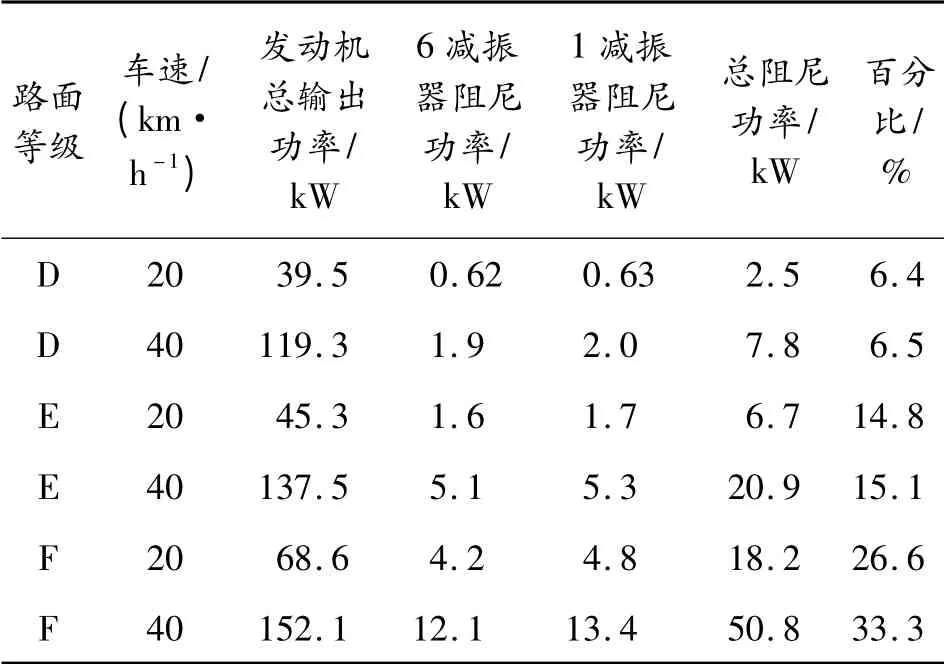
表1 减振器阻尼消耗功率
当履带车以20 km/h 行驶在F 级路面上时,减振器消耗的功率占发动机功率的26.6%,即使动力传动系的总效率η=0.8,也需消耗发动机功率的21.3%,随着车速提高这一比例还会增加,由此可见减振器消耗的阻尼功率比较大,有必要对其进行回收。
另外根据估算[4]减振器在有效工作条件下的散热功率在4 kW 左右,而车辆在E 级路面以40 km/h 行驶时,减振器阻尼功率已经超过散热功率,随着车速的提高将使减振器温度过高[7],还影响减振性能,同时制约车速的提高。
4 结论
通过Matlab/Simulink 和RecurDyn 的联合仿真分析了不同工况下悬挂阻尼的能耗、所占发动机功率的比值及其随车速、路面不平度系数的变化趋势。结果表明:悬挂阻尼耗散的能量有很大的回收价值,使用馈能型主动悬挂不但是为了回收悬挂阻尼耗散的能量,还是一种提高履带式装甲车辆越野车速的技术途径。
[1]喻凡,张勇超.馈能型车辆主动悬架技术[J].农业机械学报,2010(1):1-6.
[2]焦晓娟,张湝渭,彭斌彬.RecurDyn 多体系统优化仿真技术[M].北京:清华大学出版社,2010.
[3]丁法乾.履带履带式装甲车辆悬挂系统动力学[M].北京:国防工业出版社,2003.
[4]闫清东,张连第,赵毓芹,等. 坦克构造与设计[M]. 北京:北京理工大学出版社,2007.
[5]李惠彬.振动理论与工程应用[M].北京:北京理工大学出版社,2006.
[6]张永林.车辆道路数值模拟与仿真研究[D].武汉:华中科技大学,2010.
[7]蔡兆忠,李慧梅,安钢,等.履带车辆悬挂系统振动仿真与减振器能耗分析[J].装甲兵工程学院学报,2012,26(3):39-41.
