一种双尺度海面模型及其仿真

侯建国，祝明波，邹建武，黄佳琦，赵 骏

(海军航空工程学院电子与信息工程系，山东烟台 264001)

海洋面积占全球面积的3/4 左右，为了充分利用这个丰富的天然资源，需要对海洋进行遥感。在国防建设方面，需要利用星载雷达和机载雷达等在海洋背景下检测和识别目标。早在19 世纪，人类就开始了对海浪的研究［1］。随着计算机技术的发展，数值模拟显示了更大的灵活性和可控性，更由于它的低成本使得数值模拟海面得到了广泛的应用。国内外许多实验室都已建立模拟池来模拟实际海面进行实验测量或者外场测量，提出了各种各样的海谱模型和经验公式。海浪是空域和时域上高度不规则和不重复的物理现象，其变化形式是无法预知的。从定性的角度来讲，海面是大尺度、近似周期性的波浪叠加着波纹、泡沫和飞溅浪花。通常把大尺度波浪成为海面的大尺度结构，小尺度的波纹称为海面的微细结构［2］。对于海面建模，目前多以Fung 的半经验完全海谱模型为基础。而实际上，DV 海谱与Fung 完全海谱具有类似的特性，都是由大尺度波谱和小尺度波谱组合而成，但Fung 完全海谱大尺度波谱取值过小，DV 海谱可以看成对Fung 海谱的进一步完善。因此，本文为了丰富双尺度海面的多样性，同时更加真实地描述海面，介绍了一种基于DV 海谱模型［3］的双尺度海面的模拟方法。

1 DV 海谱模型理论

海浪在风作用下不会无限制的继续产生下去，当波浪的能量聚集达到临界状态时，风对波浪的能量输入与波浪的能量耗散相平衡，这是推导DV 海谱模型的基本依据。该模型假定海面由大尺度波浪以及叠加在其上的小尺度波浪组成，将海面波谱根据不同波数尺度分为两个区域。分段波数谱中SDV1(k)模拟大尺度海谱，SDV2(k)模拟小尺度海谱:

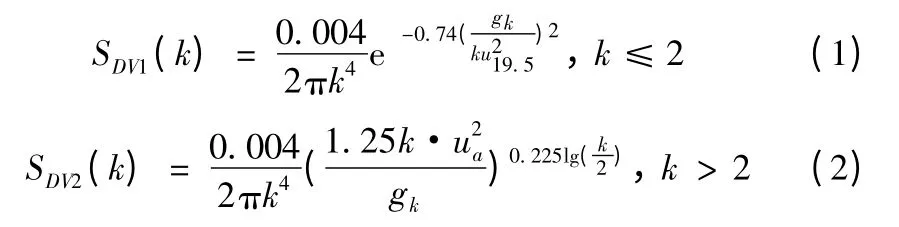
式(1)中:gk=9.81 +7.25 ×10-5k2;u19.5为19.5 m 上空风速;ua为摩擦风速;利用余弦函数来描述二维海谱［4］，体现海面在风作用下的各向异性，φ 为风向角，f(Φ)=cos2(Φ-φ)。

2 海面生成方法

海面生成方法主要分为蒙特卡罗法和线性叠加法两种方法。本文采用线性叠加法生成海面。根据随机海浪理论，海浪可看做是一平稳随机过程，其海面上任意一点的波动可多个看做无限振幅、频率和初相均不相同，不同角度方向传播简单余弦波的叠加［5-7］。二维海面可表示为

式(3)中，aij、ωi、ki、Φj、φij分别为第i 个余弦波的振幅、角速度、波数、方向角和初始相位，波数ki与频率ωi之间满足ω2=gk 的色散关系，φij为［0，2π］之间均匀分布的随机变量;(x，y)为波点位置;t 为时间矢量。

振幅aij满足瑞利分布，且有通常由下式确定

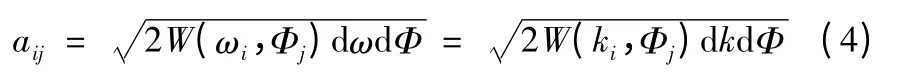
式(4)中:W(k，Φ)为二维海面的方向频率谱。

假设本文采用的海谱大尺度波与小尺度波波数分界线为k1，小尺度波数最大值为k2，把波数范围划分为M 个等波数间隔的区间，则大尺度波数间间隔为

小尺度波数间间隔为

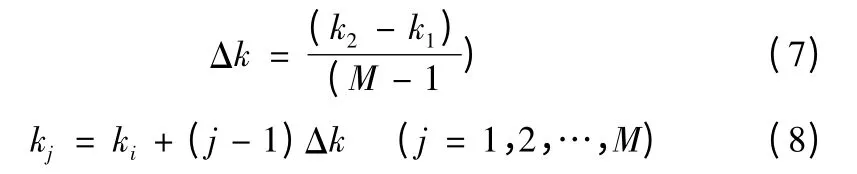
一般也可以用等分法划分方向。实际的海洋能量多分布在方向两侧的范围内，若分成N 个方位区间，则方向间隔为

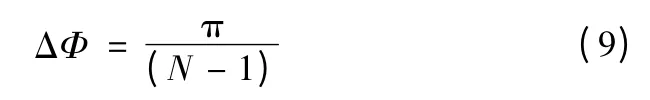
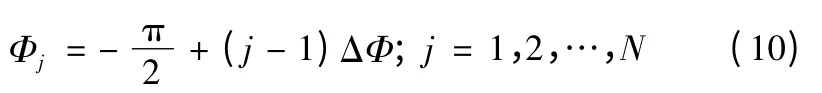
这样，式(3)可以截断为

从而，海面生成可以通过数值仿真来实现。

3 仿真分析

根据上述方法，本文用Matlab 模拟了某时刻不同风速以及不同风向的海面，模拟的海面面积为200 m×200 m。仿真结果如图1 ～图6 所示。

图1 风速为3 m/s，风向角为0°

图2 风速为3 m/s，风向角为90°

图3 风速为10 m/s，风向角为0°

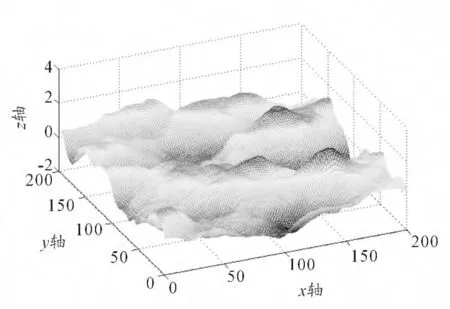
图4 风速为10 m/s，风向角为90°

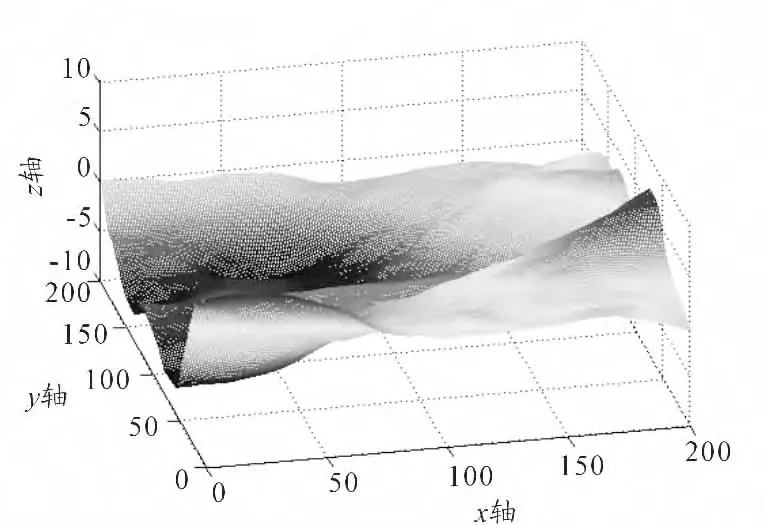
图5 风速为20 m/s，风向角为0°

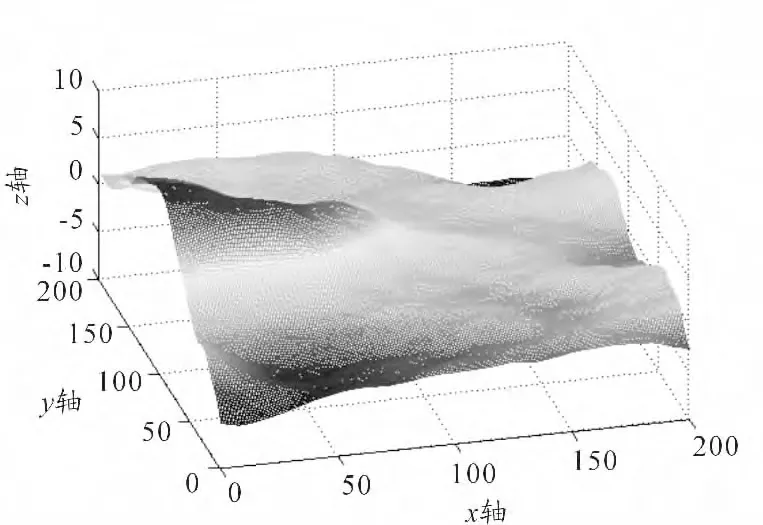
图6 风速为20 m/s，风向角为90°

仿真结果如图所示，图1 ～图6 的波高分别为0.197 6 m、0.162 9 m、3.781 0 m、4.507 5 m、14.157 2 m、13.133 3 m。综合分析图1 ～图6 可见:随着风速的增加，海面的起伏变大，粗糙度增加，海面所呈现的主波浪尺寸符合实际海况。从海面的纹理特征可以看出风向角的变化对生成海面产生的影响。由此可见，海谱的方向分布函数对于描述海面随风向变换特征是至关重要的。通过与“国际标准海况等级同浪高范围与海面特征的相互对应关系”对比，可以得出模拟出的海面符合实际海况。因此，采用DV 海谱模型仿真出的海面是有效的。

4 结束语

海面建模与仿真是海面成像模拟的关键步骤。本文采用了一种DV 海谱模型进行海面建模与仿真，对重力波与张力波的波数取值相同，采样均匀，可以看成对Fung 海谱的进一步完善。从仿真的结果分析，模拟出的海面符合实际海况。

［1］徐德伦，于定勇.随机海浪理论［M］.北京:高等教育出版社，2001.

［2］郭立新，王蕊，吴振森.随机粗糙面散射的基本理论与方法［M］.北京:科学出版社，2009.

［3］Durden S，Vesecky J.A physical radar cross-section model for a wind-driven sea with swell［J］.IEEE Journal of Oceanic Engineering，1985，10(4):445-451。

［4］Johnson J T，Chuang C W.Quantitative valuation of ocean surface spectral model influence on sea surface backscattering［R］.Tech.Report 738927-1.The Ohio State University ElectroScience Lab，2000.

［5］林亚，海面后向散射计算及其在PD 雷达导引头仿真中的应用［D］.北京:北京航空航天大学，2007.

［6］马杰，田金文，柳健，等.三维海浪场的数值模拟及其动态仿真［J］.系统仿真学报，2001，13(增刊):39-44.

［7］聂卫东，康凤举，褚彦军，等.基于线性海浪理论的海浪数值模拟［J］. 系统仿真学报，2005，17(5):1037 -1039，1044.