基于EOQ 下我国航材存储模型的实例研究
2015-07-01曹文静
苏 涛,曹文静,赵 敏
(海军航空工程学院 a.控制工程系; b.研究生管理大队,山东烟台 264001)
人们在生产和日常生活中往往将所需的物资、用品和事物暂时的储存起来,以备将来使用或消费。这种储存物品的现象是为了解决供应(生产)与需求(消费)之间的不协调的一种措施,若是航材需求与供应、消耗与存储之间存在着不协调性,其结果会产生2 种情况:一是供过于求,由于航材的积压,造成航材保障经费的大幅增加和过期航材的报废;二是供不应求,航空装备完好率得不到有效保证,以此为研究对象,利用运筹学方法去解决最合理、最经济的储存问题。
1 传统EOQ 模型的单一性与局限性
目前各航空公司多使用简单EOQ 模型(如图1 所示)来制订采购计划。此模型的运用基于下面的假设:
1)需求量是常量,反复出现并且是已知的;
2)准备时间是常量,也是已知的;
3)不允许缺货。因为需求和准备时间是常量,人们可以准确地确定订货时间来避免缺货;
4)订货或生产都是批量进行的,并且整个批量同时到达仓库进行存储;
5)使用的成本结构如下所示:货物成本是固定的,对大批量的购买也没有折扣。仓储成本是由存储平均水平线性地决定的。每批的订货成本是固定的,它与每批货物的数量无关;
6)货物是单一产品,和其他产品不发生相互作用。
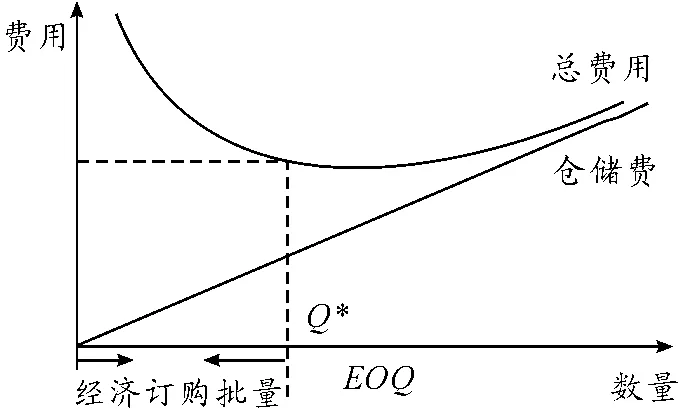
图1 航材年仓储费、订购费和总费用曲线
Q*为在以上各条假设的基础上,订货成本、仓储成本之和最低时的订货批量。考虑到航材本身的实际特点,无法满足以上各条假设,因此需要对简单EOQ 模型进行修正。
在上述假设条件下,存货的相关成本包括以下2 项:
1)订货成本。订货成本是指为组织进货所发生的各种费用,包括采购人员的差旅费、通讯费、运输费、检查费等、这些费用一般与订货的次数有关。在存货的全年需求量一定的情况下,一次订货量最多,全年的订货次数越少,订货费用越低。
2)存储成本。存储成本是指企业为持有存货而发生的费用,包括存货资金占用费用或机会成本、仓储费用、存贷保险费用等。这些费用一般与平均存货水平的高低成正比。在存货的全年需求量一定的情况下,一次订货量越多,全年的平均存货水平越高,存储费用越高。
2 存储数学模型的建立与求解
2.1 不允许缺货的成批供应模型(EOQ 模型)
不允许缺货,即设定缺货损失费为无穷大。设存储系统的输出是连续均匀的,需求量为常数(单位时间的需求量为λ、年需求量为D);当存储降到零时可以在提前订货时间T内得到补充,不会产生缺货现象;提前订货时间T 固定不变,所订购器材可以一次成批到达,存储量变化如图2 所示。
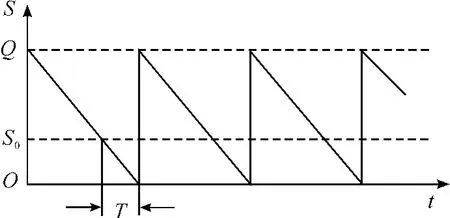
图2 不允许缺货的成批供应模型存储量变化曲线
图2中S0为订货点,即存储量下降至S0时提前订货,S0=λT。
全年的存储管理费为订货费与存储费之和,即

式中:Q 为订货量;D/Q 为全年订货次数;C1为每次订货费;Q/2 为平均存储量;C2为单位器材的平均存储量。
计算得,使全年存储管理费最少的最佳订货量为

全年最少存储管理费为

全年最佳订货次数为
2.2 不允许缺货的分批供应模型
不允许缺货的成批供应模型适用于所订购器材可以一次成批到达。由于生产或运输等多方面原因,所订购器材多数是逐次分批到达的,其存储是边补充边陆续消耗的,存储量变化如图3 所示。
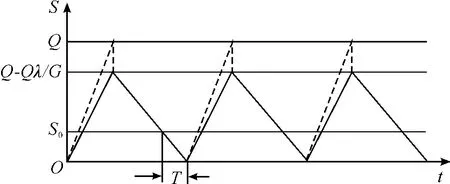
图3 不允许缺货的分批供应模型
图3中,G 为到货率,即单位时间内的到货量;Q -Qλ/G为量大存储量。
由于存储量上升率与下降率均为线性,得平均存储量为
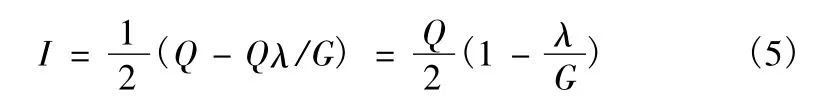
全年存储费为

全年存储管理费为

计算得使全年存储管理费最少的最佳订货量为

全年最少存储管理费为

全年最佳订货次数为

3 扩展的允许缺货供应模型
3.1 允许缺货的成批供应模型
允许缺货的成批供应模型是不允许缺货的成批供应模型的基础上,在存储管理总费用中加入了缺货损失费,其存储量变化如图4 所示。
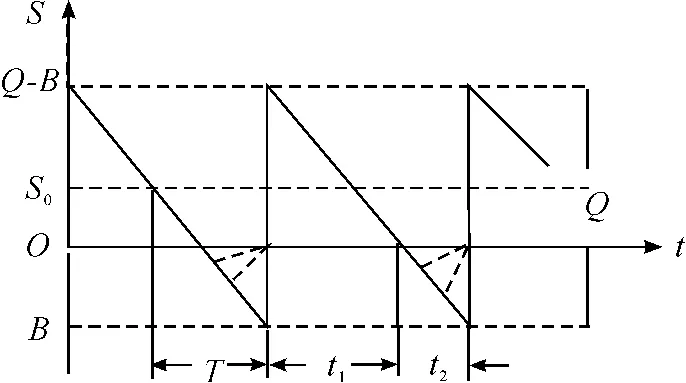
图4 允许缺货的成批供应模型存储量变化曲线
图4中:t1为存储有货时间;t2为允许供应缺货时间;B为允许缺货量;Q-B 为最大存储量。全年存储管理费为

计算得,使全年存储管理费最少的最佳订货量为
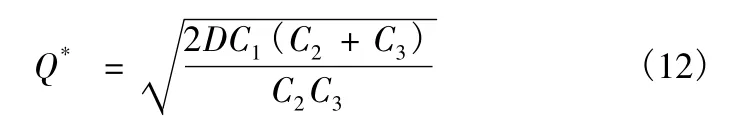
全年最少存储管理费为
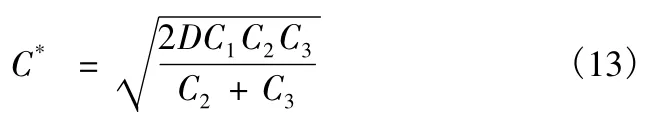
全年最佳订货次数为
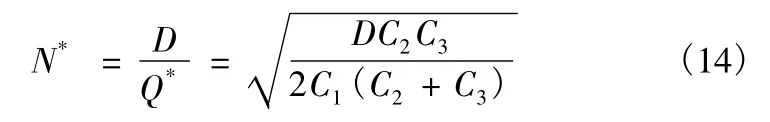
比较允许缺货的成批供应模型和不允许缺货的成批供应模型,允许缺货的成批供应比不允许缺货的成批供应的最佳订货量增加了倍,全年最佳订货次数和最少存储管理费均下降了倍。
3.2 允许缺货的分批供应模型
允许缺货的分批供应模型,其存储量变化如图5 所示。

图5 允许缺货的分批供应模型存储量变化曲线
图5中:t1为存储量从0 增加到全部到货(存储量最大)所需时间;t2为存储量从最大值下降到0 所需时间;t3为存储量为0 到订货开始到达所需时间;t4为从订货开始到达至补够缺货所需的时间;Q-B 无实际物理意义;Q-B-(t1+t4)λ为最大存储量。
建立模型,解得使全年存储管理费最少的最佳订货量为
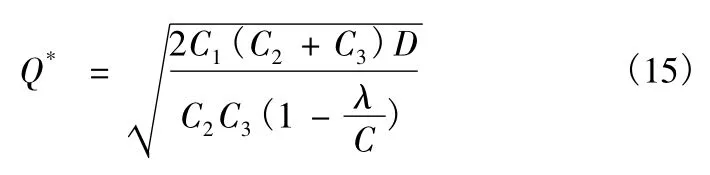
全年最少存储管理费为

全年最佳订货次数为
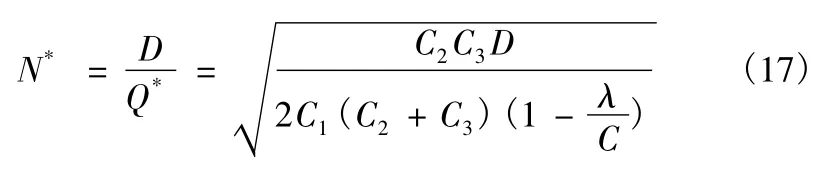
比较允许缺货的分批供应模型和不允许缺货的分批供应模型,允许缺货的分批供应比不允许缺货的分批供应的最佳订货量增加了倍,全年最佳订货次数和最少存储管理费均下降了倍。
4 实例求解
1)例1 设某部每天所需要的某型航材量是相同的,每年需要1 000 kg,每年该型器材的存储费为5 元/kg,每次外出订货需要订货费100 元,若每次订货数量不限,订货后能够在存储量为零时一次成批到货,怎样组织订货才能使该型航材的存储管理费最少。
根据题意,已知D=1 000,C1=100,C2=5,计算得,最佳订货量为
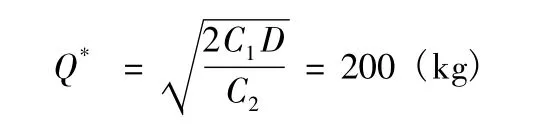
全年最佳订货次数为
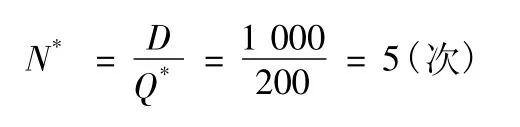
全年最少存储管理费为

2)例2 承例1,若订购航材为陆续到达,每天到货量为30 kg,试求最佳订货量Q*。
根据题意,已知D =1 000,C1=100,C2=5,λ =1 000/365≈2.74(每年按365 天计算),G =30,计算得,最佳订货量为


全年最佳订货次数为全年最少存储管理费为

3)承例1,若订购航材允许缺货,可在下批货到时补上,但缺货损失为每年每件损失费为100。根据式(12)、式(13)、式(14)可以得到:

4)承例2,若订购航材允许缺货,可在生产需要一定时间情况下,缺货损失费为每年每件损失费为100。根据式(15)、式(16)、式(17)可以得到:
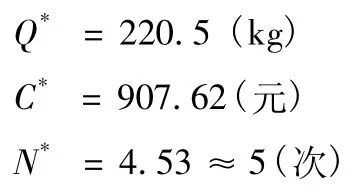
5 结果分析
1)通过以上对比研究可以得出,分批供应要比成批供应节省存储管理费,但是分批供应一般会增加库存管理工作量。允许缺货条件下的模型比不允许缺货条件下的模型的最佳订货量增加了倍,全年最佳订货次数和最少存储管理费均下降了倍。
2)建立的模型是确定性的,即一个周期内的需求量是已知的。如果不是这样的话,更合适的模型将是随机的(或概率的),也就是一个周期内的需求量是一个已知分布的随机变量。
3)本文不仅考察了基本经济批量模型的确定型库存问题的研究,对EOQ 模型的进一步扩展也有所展开,比如允许缺货条件下的分批供应模型和允许缺货条件下的成批供应模型等,对有效降低总的存储费用有较好的研究价值。
[1]韩伯棠.管理运筹学[M].北京:高等教育出版社,2003.
[2]魏国华,傅家良,周仲良.实用运筹学[M].北京:清华大学出版社,2000.
[3]胡运权,郭耀煌.运筹学教程[M].北京:清华大学出版社,2002.
[4]邓成梁.运筹学的原理和方法[M].2 版.武汉:华中科技大学出版社,2002.
[5]余兴无,李旭东.确定性存储基本模型的几个推广[J].甘肃科学学报,2002(02):76- 79.
[6]陈晓芳,岳才保.动态存储模型研究[J].武汉理工大学学报,2003(01):88- 91.
[7]胡运权,郭耀煌.运筹学教程[M].北京:清华大学出版社,2003.
[8]姜启源,谢金星,叶俊.数学模型[M].北京:高等教育出版社,2003.
[9]杜廷松.订货问题的一个最优存储模型[J].商场现代化,2007.
[10]赵经成,祝华远,王文秀.航空装备技术保障运筹分析[M].北京:国防工业出版社,2010.
[11]左洪福,蔡景,吴昊,等.航空维修工程学[M].北京:科学出版社,2011.
[12]李晓阳.从航材仓储看成本管理[J].民航经济与技术,2001(1):28-30.
[13]何爱云.浅谈美联航材库存管理[J].民航经济与技术,2000(11):11-14.
[14]周洁敏.民用航空特色专业系统教材[M].北京:科学出版社,2010.
[15]王晓迪. 高等学校教育装备管理决策支持研究[EB/OL].[2011 -12 -01]. http://cdmd. cnki. com. cn/Article/CDMD-10217-1012518514.htm.
