基于距离高分辨反舰微波导引头的目标检测方法

李如刚，张 林，马 良

(1.中国人民解放军91278 部队，辽宁大连 116041;2.海军大连舰艇学院 a.导弹系; b.导弹舰船指挥系，辽宁大连 116018)

反舰导弹微波导引头采用FMICW 等新体制，既可保证良好的收发隔离度，又能实现较好的距离高分辨，提高导弹的干扰识别和抑制能力，是未来的重要发展方向。由于导弹末端突防通常采用掠海飞行，海杂波环境存在较明显的海浪尖峰效应，且距离高分辨微波导引头的距离分辨单元长度远小于舰船的几何尺寸，捕捉目标时目标的回波将会被展布在导引头不同距离分辨单元内，出现一维距离像的“距离扩展目标”现象，因此，这种低掠海角、距离高分辨条件下的目标检测与低分辨力条件下有着十分明显的区别，需要进行深入分析和研究。

1 微波导引头检测模型与最优检测器分析

传统微波导引头具有较高的杂噪比下，海杂波相比于接收机内部噪声对目标检测的影响更大，因此进行目标检测时，可暂时不考虑接收机内部噪声的影响。假设非相参积累的调频周期数为P，接收距离波门的宽度为R 个距离分辨单元，且每个距离单元仅包含一个回波复采样数据，扩展目标的回波分布于其中某段长度为L 的数据段中。由此可见，用于检测的回波数据长度为H=RP，目标检测的假设检验模型描述如下

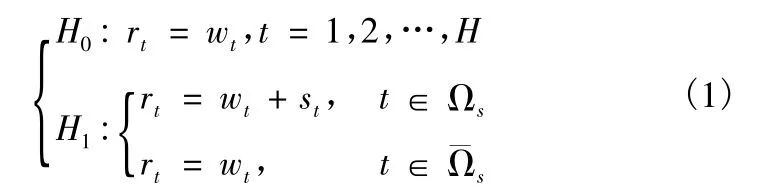
式中:Ωs为包含目标回波的数据集合={1，2，…，H} -Ωs;st，wt分别表示扩展目标的回波和高分辨海杂波，且两者相互独立。假定回波信号st的幅度服从参数为A2的Rayleigh 快起伏模型，相位在［0，2π］内均匀分布;假定高分辨海杂波wt的幅度服从复合高斯分布，{wt}相互统计独立［1］，且wt=τtgt。其中，gt为海杂波的斑点分量，服从零均值复高斯分布，它的方差为1;τt为海杂波的纹理分量，服从广义χ2分布。

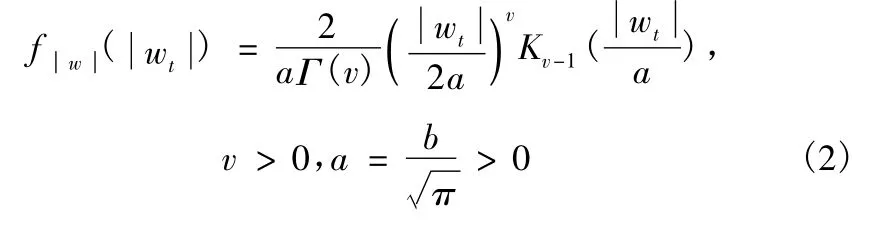
式中:a 为海杂波强度的尺度参数;v 为形状参数，它决定了K分布的形状，其值越小，K 分布的峰态越陡峭，拖尾越长，尖峰特性越明显。测量结果表明:0.1≤v ＜∞，且当v→∞时，K分布退化为Rayleigh 分布。

K 分布的各阶原点矩为

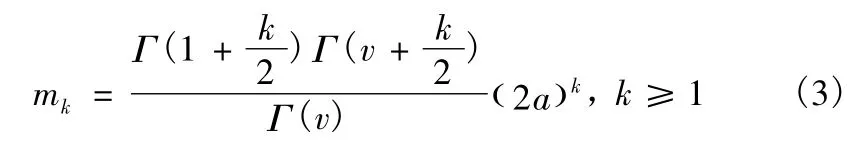
为了便于分析，假定海杂波的分布参数已知或者可以利用杂波数据精确估计。此外，对于微波导引头而言，虽然末端突防过程中导弹与舰船的高速相对运动会导致目标距离像的跨距离单元走动，但由于舰船的速度相对很低，利用高精度弹载惯导装置的速度信息进行运动补偿后，距离像散射中心的跨距离单元走动问题可以有效地解决。因此，在下面的分析过程中，可不考虑目标距离像跨距离单元走动的问题。

在纽曼-皮尔逊准则下，式(1)描述的假设检验的最优检测器为似然比检测器(likelihood ratio test，LRT)，它的表达式为

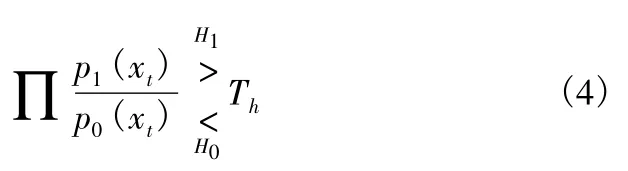
其中:p1(xt)是xt在H1假设下的概率密度分布函数;p0(xt)是xt在H0假设下的概率密度分布函数;Th为相应的门限值。

令f(rt)=lnp1(rt)-lnp0(rt)，则式(4)可以表示为

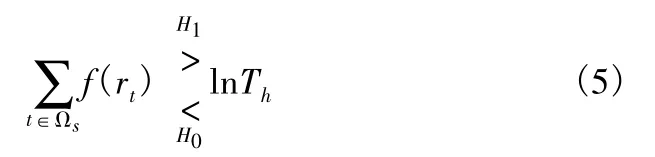
即为微波导引头二进制检测的理论最优标准。

2 基于多周期积累最优二级二进制检测的设计与优化

基于多周期积累最优二级二进制检测的思想是:首先通过幅值检测器检测将高分辨距离像二值化，然后利用滑窗搜索的方式进行周期内的M/N 积累检测(空域二进制检测)，最后再进行周期间的M/N 积累检测(时域二进制检测)。

2.1 检测器设计

由于海浪尖峰回波是稀疏分布的且瞬态能量很强，基于多周期积累的最优二级二进制检测正好利用了海杂波尖峰效应的这一特点。首先，幅值检测对回波进行二值化处理大大地削弱海浪尖峰回波瞬态能量的影响，有效地抑制了海浪尖峰的干扰;其次，海浪尖峰在时间、空间上的分布是稀疏的，其回波通过幅值检测器门限的概率很低，经过时域和空域积累后，稀疏分布的海浪尖峰很难超过检测门限，而舰船目标是人造物体，具有稳定的外形结构，其回波在时间、空间上是连续出现的，经过时域、空域积累后很容易达到门限要求。因此，基于多周期积累的最优二级二进制检测器可大幅度降低海尖峰引起的虚警概率。另外，由于采用了非相参积累的检测方法，检测器不需要多普勒导向矢量(Steer Vector)信息，简化了检测器实现的难度。由此可见，利用多周期积累的最优二级二进制检测器进行K 分布海杂波环境下的目标检测是一条可行的技术途径。

步骤1:幅值检测

若zp，l＞T，则，否则。通过幅值检测，可以有效地削弱海浪尖峰回波瞬态能量的影响。

步骤2:调频周期内滑窗积累检测。由于无法确定Ωs在全部数据中所处的位置，因此，周期内的积累检测采用滑窗搜索的方式进行，令lw∈{0，1，…，R -N +1}。检测器可以表示为

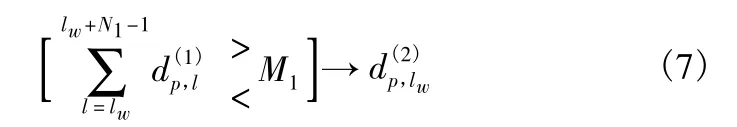
步骤3:令N2=P，进行周期间的积累检测

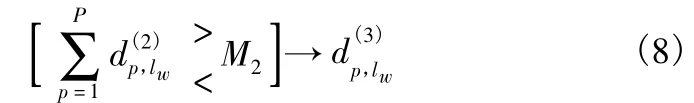
2.2 虚警概率分析

由于各个距离分辨单元内的海杂波是相互独立的，故幅值检测的虚警概率Pf1和周期内积累检测的虚警概率Pf，2的关系可以表示为

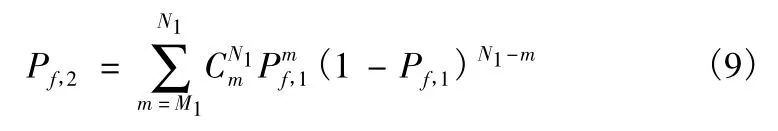
其中，Pf，1和第一门限T 的关系为

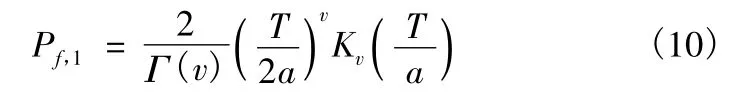
二级二进制检测器的总虚警概率Pf可以表示为

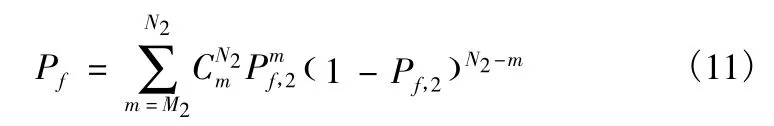
经过周期内的M/N 积累检测后，检测器的检测概率为

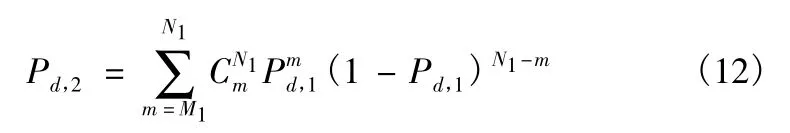
其中，Pd，1为幅值检测器单次检测的概率，可表示为

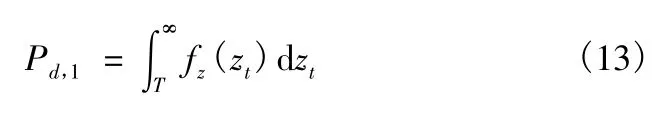
式中，zt的概率密度函数可以表示为［3］

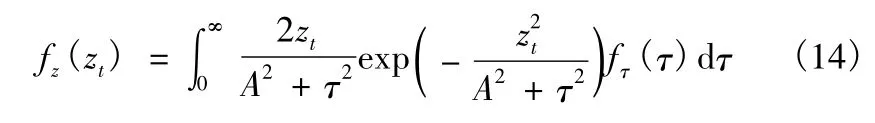
由此，可以得到检测器的总检测概率Pd为

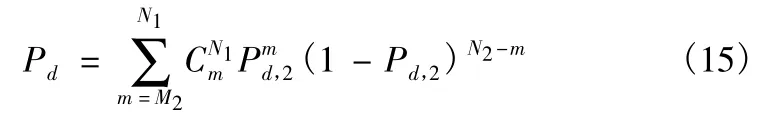
由上述推导过程可知，检测器的检测概率Pd、虚警概率Pf与检测门限T、参数M1，M2之间的数学关系比较复杂，只能通过数值计算的方法进行分析求解。利用式(9)、式(10)和式(11)进行数值仿真得到的海杂波形状参数v、第一检测门限T 与M1，M2的关系如图1 所示，其中a =1，Pf=10-6，N1=N2=30，M1=M2。由图1 可知，当参数M1，M2确定时，检测门限T 随着v 的增大而增大;当形状参数v 确定时，检测门限T 随着M1，M2的增加而显著降低。同时，由于检测器采用了多周期的非相参积累，检测门限值T 相对较低，一般不超过23.0 dB，有利于低信杂比条件下目标信号的检测。

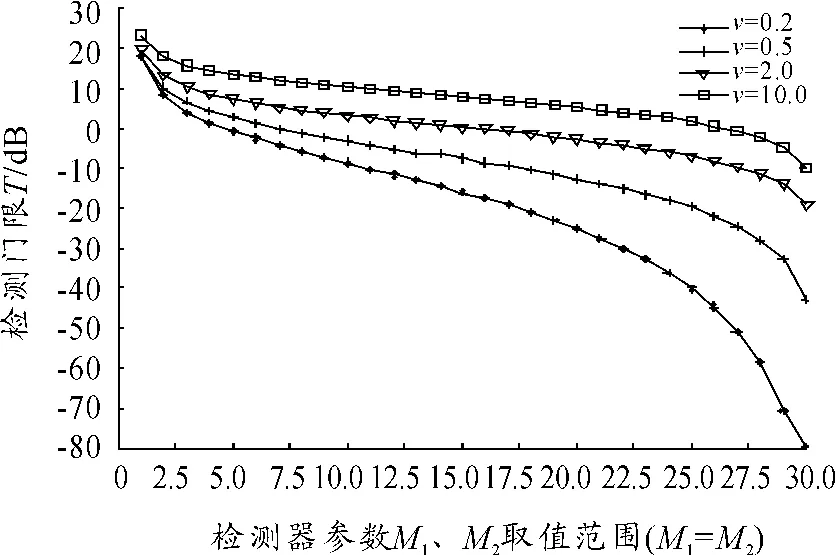
图1 检测器的检测门限T 与参数M1、M2 的关系

2.3 检测器参数优化

对于距离高分辨反舰微波导引头而言，其最优检测器的结构由海杂波的统计特性和扩展目标的散射特性共同决定，这两者是影响检测器检测性能的最主要的因素。同样地，基于多周期积累的最优二级二进制检测器也不例外。为了使海杂波环境下检测器的检测性能达到最优，需要根据纽曼-皮尔逊准则，对检测器的参数进行合理的设计，实现基于多周期积累的二级二进制检测器的参数最优选择。

这里的“最优”，指的是在给定虚警概率Pf和发现概率Pd的条件下，所需要的输入信杂比最小。另一方面，考虑到多周期积累二级二进制检测待求解的最优参数比较多，若不对参数进行一定的限制，求解过程将变得复杂甚至导致无解，因此，对检测器的参数进行如下的约束［2］

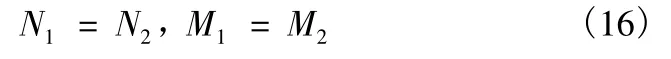
式中:N1，N2分别受目标长度和积累周期数的限制;M1，M2与目标的散射特性有关。基于多周期积累的二级二进制扩展目标检测最优参数选择参照点目标二进制检测的最优门限的确定办法［4］，其基本思路为:首先由式(10)、式(13)得到Pf1、Pd1和输入信杂比之间的关系曲线，然后再利用式(11)、式(15)求解检测器的第二、三门限和所需输入信杂比之间的关系曲线，从中得到“最优”的检测器参数。

扩展目标回波与海浪尖峰在径向展布上有着不同的特点，这一不同正是海杂波环境下扩展目标二进制检测的基本依据。具体而言，当采用K 分布来模拟海杂波幅度统计特性时，形状参数v 决定了雷达回波中海浪尖峰的显著程度;当目标幅度服从Rayleigh 快起伏模型时，目标的径向长度L 也是一个重要的参量。由此可见，参数v 和L 共同决定了检测器的最优参数。本节采取数值分析的方式研究v、L 与检测器最优参数之间的关系，归纳总结最优参数设计的经验公式和基本原则。

2.3.1 影响基于多周期积累的最优二级二进制检测性能的因素分析

根据式(9)～式(15)，分析参数v、L 对多周期积累的最优二级二进制检测器的检测性能的影响。定义单元平均信杂比(SCR)为其中为杂波的单元平均功率。假设检测器的虚假概率Pf=2. 5 ×10-6，检测概率Pd=0.9。

1)扩展目标径向长度L 与检测器性能的关系

从图2 可以看出，目标的径向长度L 越小，检测所需的SCR 就越高，检测器的检测性能也就越差，并且当目标径向长度L ＜M 时，检测器将无法实现正常的目标检测。由此可见，检测器的检测次数N1，N2应该根据目径向标长度L 来确定，通常选择N1=N2=L，同时检测门限M1，M2的大小也应满足M1=M2＜L。

2)M1，M2与海杂波形状参数v 的关系

不同海杂波形状参数v 条件下的检测器性能如图3 所示。从图3 可以看出，当选择N1=N2=L =30 时，对于每个形状参数v，都存在一个最优的Mopt∈{1，2，…，N}，使得检测器的性能达到最优状态，即在给定虚假概率Pf和检测概率Pd的情况下，M1=M2≜Mopt时所需的信杂比最小。同时，图3 反映了海杂波形状参数v 越小，即海浪尖峰越明显的时候，检测器的Mopt越大。

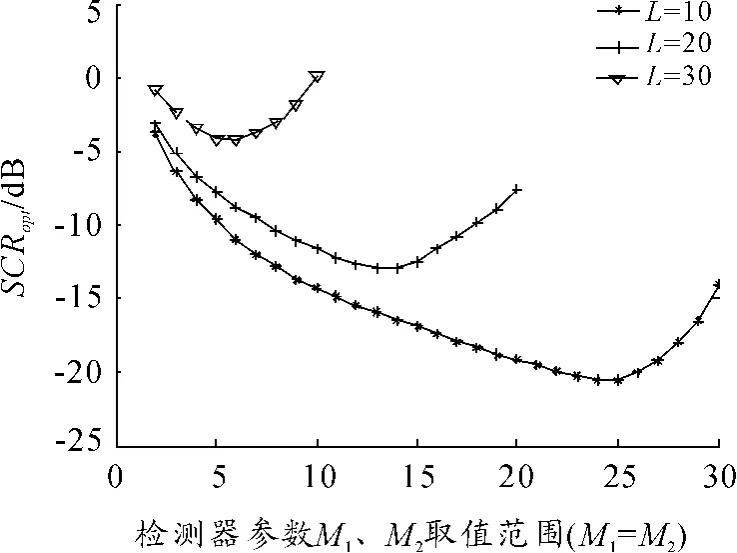
图2 N=30，v=0.2 时不同目标长度条件下检测器检测性能对比

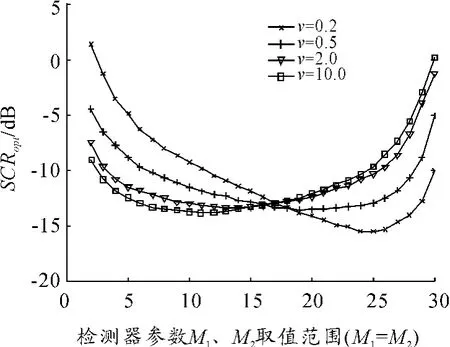
图3 不同海杂波形状参数下的检测器性能对比

在工程实现过程中，Mopt的选择区间可以进一步扩大，与SCRopt相比输入信噪比的变化不超过0.2 dB 时的M 都可以认为是“Mopt”。通过仿真计算得到了Mopt与海杂波形状参数v 的关系，如图4 所示。由图4 可知，随着形状参数v 的增大，Mopt逐步地减小，且对于较小的v，Mopt的取值范围也比较小，而对于较大的v，Mopt的取值范围也相对较大，特别地当v→∞时，Mopt将保持在一定范围内基本不变。这是因为:当形状参数v 较小时，海杂波存在明显的海浪尖峰效应，尖峰的数量相对较多，此时选择大的M1，M2可有效降低虚警概率;随着v 的增大，海杂波的尖峰效应逐渐减弱，此时不需要选择太大的M1，M2就可满足检测需求，维持较低的虚警概率，所以Mopt随v 而降低;特别地，当v→∞时，K 分布逐渐地退化为Rayleigh 分布，此时Mopt已不再随形状参数v 的变化而变化了。

3)检测器最优参数下的检测性能与海杂波形状参数ν的关系

图5 中给出了N1=N2=L=30 时，在给定虚假概率和发现概率的条件下所需的SCR 与形状参数v 之间的关系。从图5 中可以看出，随参数v 的增加，SCRopt基本上也随之增加。此外，当参数v 较小时，SCRopt随参数v 增加的趋势比较明显;而当参数v 较大时，SCRopt就基本上保持不变了。这种情况正说明:当v 较小时，海浪尖峰占据了海杂波的大部分能量，而基于多周期积累的最优二级二进制检测可以较好地抑制海浪尖峰，使得低SCR 的扩展目标检测成为可能。因此，本文提出的检测方法特别适应于低入射角、高海情条件下的扩展目标检测。

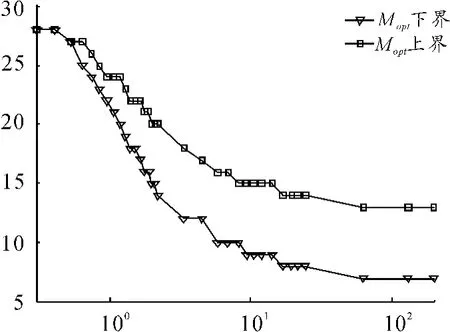
图4 N1 =N2 =L=30 时Mopt与v 的关系

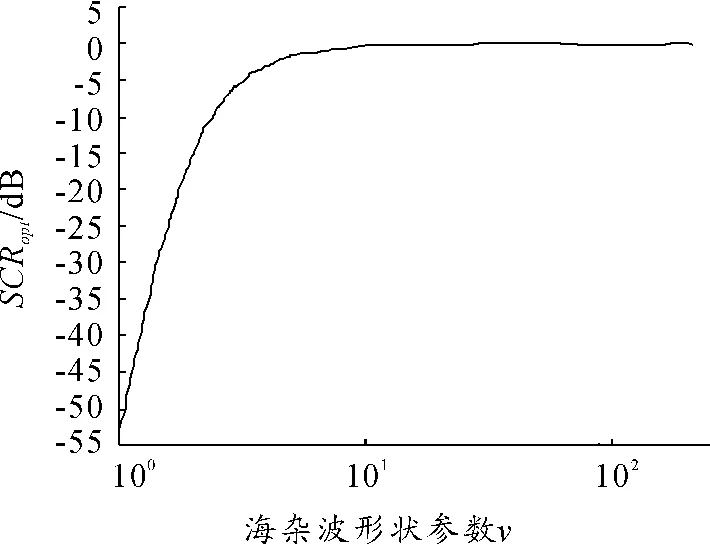
图5 各Mopt下满足检测性能指标需要的SCR 与v 的关系

2.3.2 基于多周期积累的二级二进制检测最优参数的经验公式

为了充分反映舰船目标特性，选取不同的目标径向长度值(取值范围为5≤L≤30)，经过类似的数值计算求得不同海杂波形状参数v 所对应的Mopt，在通过曲线拟合的方式获得了检测器最优参数的经验拟合公式为

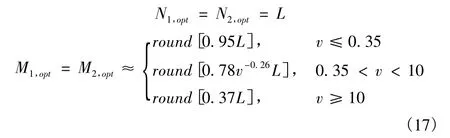
式中，round［·］表示四舍五入的取整运算。

对于经验公式(17)，需要明确的是:

1)在检测性能差异不超过0.2 dB 的约束条件下，对于不同的N 值，式(17)都可近似成立。

2)进一步的仿真分析表明，式(17)表示的经验公式的适应范围可推广至10-10≤Pf≤10-4，0.5≤Pd≤0.95。

3)信噪比变化不超过0.2 dB 的约束条件下，M1，opt=M2，opt=Mopt有一定的取值范围。因此，式(17)并不是唯一的经验公式，但它为海杂波环境下的扩展目标最优二进制检测器设计提供了重要的依据。

2.3.3 基于多周期积累的最优二级二进制检测的最优参数设计原则

由以上分析，多周期积累的最优二级二进制检测的最优参数的基本设计原则如下:

1)首先选定N1，opt，N2，opt，一般N1，opt，N2，opt=L。若小尺寸目标和大尺寸目标同时存在于导引头的探测范围内，N1，opt，N2，opt的选择需要根据实际背景的需求确定。这是因为，如果N1，opt，N2，opt的选择过大，则导引头对小尺寸目标的检测将受到影响;同样，N1，opt，N2，opt的选择过小会影响导引头对大尺寸目标的检测。实际应用中，若导引头对大目标感兴趣，N1，opt，N2，opt的选择应以大尺寸目标的长度为基准;同理，若对小目标感兴趣，则N1，opt，N2，opt的选择应以小尺寸目标的长度为基准。

2)选择M1，opt=M2，opt=Mopt＜L，且M1，opt，M2，opt的选择与海杂波形状参数v 有关。v 越小，M1，opt，M2，opt应越大;v 越大，M1，opt，M2，opt应越小。实际应用中可根据目标的散射特性的不同，合理地选择经验公式;但如果目标散射中心的能量是非均匀分布的，则检测概率计算将变得异常复杂，数值计算的方法很难得到确切的数值，此时只能采用蒙特卡洛仿真的方法进行具体问题具体分析。

此外，对于检测器扩展目标长度获取问题，可以通过其他途径来解决。具体地，对于反舰导弹而言，目标长度的先验信息可以从作战体系的其他探测设备获取。此外，由于舰艇目标的机动性远差于反舰导弹，所以在导弹高速接近目标的过程中，目标径向长度可以认为是不变的。

3 试验参数设定与数据分析

由于提出的扩展目标检测方法立足于工程实际应用，利用数值仿真的分析方法不能完全反映检测器的真实性能，因此作者结合实测的海杂波数据和目标数据综合验证基于多周期积累的最优二级二进制检测器的实际性能，并通过与最佳检测器(LRT)的对比分析来验证其在实测海杂波背景下的性能优越性。

3.1 目标检测参数设定

设定检测器的虚警概率为Pf=6.67 ×10-5，检测概率Pd=0.9，舰船目标的径向投影长度为30 m，即目标占据的距离单元个数L =20。同时，根据经验公式设定检测器的参数为:N1=N2=20，M1，opt=M2，opt=［0.37 ×20］=7。

3.2 检测器检测性能数据分析

对包含典型舰船回波的数据段，分别利用最优参数检测器和2 个非最优参数检测器进行目标检测，对比分析它们的检测性能。其中，2 个非最优检测器的参数分别设定为:M1=M2=3，N1=N2=20;M1=M2=13，N1=N2=20。利用这3 个检测器分别对截取的数据段进行目标检测，得到的检测结果如图6 所示。

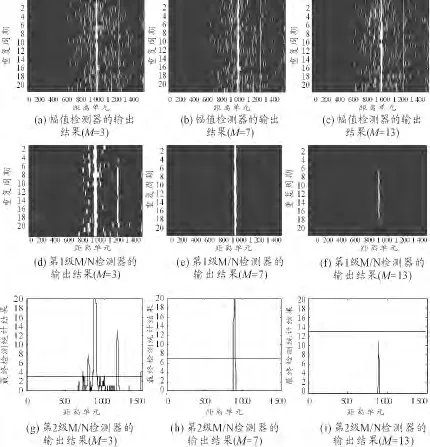
图6 不同参数的多周期积累二级二进制检测器性能对比

由图6 可知，最优参数检测器的检测性能明显优于其他2 种非最优参数检测器。当参数M1、M2设置过低时，检测器会引起较高的虚警;而参数M1、M2设置过高时则会导致检测器无法正常检测到目标。因此可以推断利用经验公式计算得到的检测器参数在实测数据下也是最优的。

4 结束语

本文的研究与分析表明，在实测海杂波条件下基于多周期积累的最优二级二进制检测器能够准确地检测出目标，且检测性能明显优于LRT 检测器，为距离高分辨反舰微波导引头的目标检测提供了一种新的技术思路。

［1］Ernesto Conte，Antonio De Maio，Ricci G. GLRT-based adaptive detection algorithms for range-spread targets［J］.Signal Processing，IEEE Transactions on，2001，49(7):28-31.

［2］Blunt S D，Gerlach K，Heyer J. HRR Detector for Slow-Moving Targets in Sea Clutter ［J］. Aerospace And Electronic Systems，IEEE Transactions On，2007，43(3):45-48.

［3］Griffiths H.Sea Clutter:Scattering，the K Distribution and Radar Performance (Ward，K. D.，et al.; 2006)(Book Review)［J］.Aerospace and Electronic Systems Magazine，IEEE，2007，22(1):33-37.

［4］丁鹭飞，张平.雷达系统［M］.西安:西北电讯工程学院出版社，1984.