某小口径凸轮炮开锁力矩有限元分析
2015-07-01戴劲松王茂森开亚骏
戴劲松,易 智,王茂森,开亚骏
(南京理工大学机械工程学院,南京 210094)
火炮的开锁过程即炮弹击发后膛内火药气体压力降到一定值时,处于闭锁状态的闩体在相应机构的驱动下完成解锁的动作,此过程是自动机射击循环动作中十分重要的一个环节,其动态特性直接决定了火炮的整体性能,设计良好的开锁过程可以确保零件的寿命和工作可靠性,而发生故障将导致自动武器工作停止,因此开锁过程的合理设计和开锁力矩的精确计算是自动武器设计中十分重要的一环[1]。
开锁过程是一个包含弹塑性变形、接触、摩擦等复杂因素的瞬态动力学过程,传统的理论计算仅用数学模型很难准确的描述开锁过程,本文应用瞬态动力学有限元软件ANSYS Workbench 对某小口径凸轮炮的击发及开锁过程进行了仿真,给出了开锁力矩的计算方法和开锁力矩随时间的变化曲线,对影响开锁力矩的因素如药筒和身管初始间隙、摩擦系数作出了定性关系的分析。
1 基于动态弹塑性理论开锁力矩分析
计算涉及弹塑性材料和动态问题,应用非线性有限元软件ANSYS Workbench 分析求解,该软件非线性求解器使用牛顿—拉斐逊方法解非线性方程,它迫使在每一个载荷增量的末端解达到平衡收敛(在某个容限范围内)[2]。
牛顿—拉斐逊求解非线性结构的平衡方程式为

或

用牛顿—拉斐逊迭代方法,开始时按线性理论求解位移δ1作为第一次近似解,之后按式:

可以看出,δ2就是位移第二次近似解,依此不断重复,直至获得收敛解为止[3-4]。
收敛准则按米塞斯屈服条件:

其中:σ1、σ2、σ3为主应力;σs为屈服极限。
本文有限元计算模型包括药筒、身管、身管支撑体和闩体4 个零部件,金属药筒是一个薄壁厚底的圆筒形容器,且药筒前端厚1.1 mm,后端厚1.5 mm,由闩体夹持底缘输送到身管中,药筒与身管初始间隙为0.3 mm,身管固连在身管支撑体中,身管支撑体的后端有7 个闭锁齿,用来与闩体的闭锁齿配合,即闭锁后用来承受火炮射击产生的膛底合力,闩体与药筒底部及闩体与身管支撑体闭锁齿初始间隙均为0.02 mm,具体模型如图1 所示。

图1 有限元模型
零部件之间按实际运动情况添加摩擦接触关系,摩擦系数为0.2,身管和身管支撑体之间添加绑定接触关系,可视为一个零件。
火药气体膛压作用以压力载荷形式施加在药筒内壁,据实验数据得最大膛压为305.73 MPa,膛压曲线如图2 所示。
身管、身管支撑体和闩体材料为炮钢,药筒材料为S20材料,均为线弹性材料,屈服模型采用双折线(Bilinear Isotropic Hardening)模型,不考虑材料的热变形,材料具体属性见表1 所示。

图2 膛压曲线

表1 材料属性
开锁过程如下:火炮击发后,火药气体迅速膨胀,药筒在气体压力下开始变形,开始压力较低,药筒的变形反力能与之相平衡,此时药筒的变形符合胡克定律发生弹性变形,由于药筒的弹性变形很小,因此药筒很快就进入塑性变形,且由于药筒口部较薄,径向运动率先贴膛,带动身管一起膨胀,身管屈服应力很大,在该膛压下只发生弹性变形,由于火药气体作用于药筒底部,药筒轴线运动使得药筒底部贴向闩体,挤压闩体并使闩体向后运动贴紧身管支撑体,在膛压逐渐增大至最大膛压时,药筒由前往后逐步贴膛,但由于靠近药筒靠底部位置比较厚,会形成一段不贴膛段,并在此位置处药筒发生最大变形。膛压逐渐降低时,身管和药筒弹性变形部分随膛压下降而恢复,因药筒发生了塑性变形,而不能完全恢复,身管反向压缩药筒,身管支撑体和闩体也逐渐恢复,压紧药筒底部。膛压降至一定值后,开锁机构开始运动,带动闩体旋转25.7°开锁,药筒贴膛力远大于药筒底部和闩体接触力,因此开锁过程中药筒不旋转,闩体旋转过程中主要受到药筒底部与闩体的挤压力和闩体与身管支撑体闭锁齿的挤压力,开锁力矩即这两个接触区域的摩擦力矩。
2 开锁力矩仿真结果及分析
药筒在膛压作用下0.4 ms 时发生了塑性变形,在0.9 ms 时膨胀至贴膛,药筒受到最大应力为361.9 MPa,膛压下降至最小时,由于药筒发生塑性变形内部仍有残余应力,药筒与身管接触应力为107.48 MPa,药筒底部与闩体接触应力为240.37 MPa。开锁机构带动闩体旋转开锁时,药筒与身管接触应力产生的摩擦力矩可由下列公式推导得到
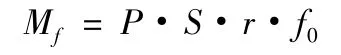
其中:P 为药筒与身管接触应力,S 为接触面积,r 为药筒外壁平均半径,f0为当量摩擦系数。
药筒底部与闩体接触应力产生的摩擦力矩由下列公式可推导得到

其中:Q 为药筒底部与闩体接触正压力,其大小为接触应力与接触面积之积,f 为摩擦系数,r 为当量摩擦半径[5]。
假设药筒侧面和底面各自完全贴合,由以上两个公式得到药筒与身管接触应力产生的摩擦力矩为4.1 ×105N·m,药筒底部与闩体接触应力产生的摩擦力矩为6.26 ×103N·m,因此闩体旋转开锁时药筒不随闩体旋转,仅药筒底部与闩体产生滑动摩擦。
由以上分析可知:开锁力矩即药筒底部与闩体产生的摩擦力矩和闩体与身管支撑体闭锁齿产生的摩擦力矩之和,经仿真得到两部分摩擦力矩,开锁力矩随时间变化曲线如图3所示。
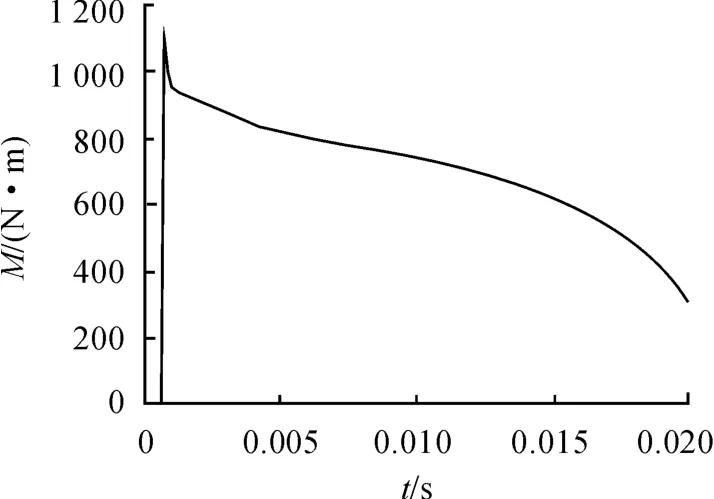
图3 开锁力矩—时间曲线
由图3 可以看出,开锁力矩在闩体旋转开锁的瞬间由0增大到最大值1 164.6 N·m,然后又急剧下降至963.9 N·m,此过程仅用时0.3 ms,在此之后,15 ms 之前,开锁力矩以近乎负线性关系缓慢减小到615.8 N·m,15ms 之后,开锁力矩又以很快的速度下降到304.9 N·m[6]。
开锁力矩从0 瞬间上升到最大值,是因为开锁机构驱动闩体旋转运动,摩擦阻力从0 达到最大静摩擦力,之后闩体便进入滑动摩擦的范畴。开锁力矩急剧下降的过程是因为闩体由静止到开始旋转,闩体与药筒底部、身管支撑体闭锁齿接触区域会出现些许松动,导致接触面上正压力下降。之后逐渐下降的过程,主要是因为闩体闭锁齿与身管支撑体闭锁齿之间由完全啮合到慢慢分离,接触面积的减少引起了正压力的变化,开锁结束前一段快速下降的曲线是因为身管支撑体闭锁齿是梯形的缘故,接触面积的急速减少使得开锁力矩下降较快。有限元仿真结果与理论预想情况基本符合,仿真数据对开锁过程中主要零部件的优化设计提供了参考价值。
3 开锁力矩影响因素分析
影响开锁力矩的因素方方面面,且多因素综合改变着开锁力矩的大小,本文仅分析对比主要的两个影响因素: 开锁力矩随药筒与身管初始间隙、摩擦系数。在原有模型上进行有限元参数化仿真分析,通过控制变量法进行多次仿真,得到开锁力矩随药筒与身管初始间隙、摩擦系数两个主要因素的变化情况。
图4 是不同初始间隙下开锁力矩的对比,由图看出,开锁力矩在初始间隙的影响因素下变化幅度不大,但是在初始间隙0.3 mm 时开锁力矩出现最小值。由图5 更加清楚地看出,0.3 mm 左右出现极小值,之后随着初始间隙的增大,开锁力矩随之逐渐增大,但初始间隙达到0.5 mm 左右,开锁力矩基本不再变化,趋于一个定值,而且综合考虑初始间隙对火炮发射其他方面的影响,如抽壳力、发射威力等,因此通过改变初始间隙值而减小开锁力矩是很有限的。
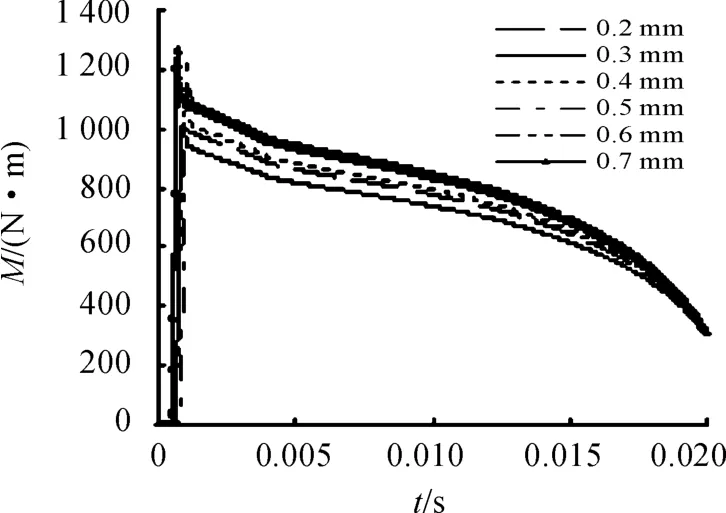
图4 不同初始间隙下开锁力矩对比
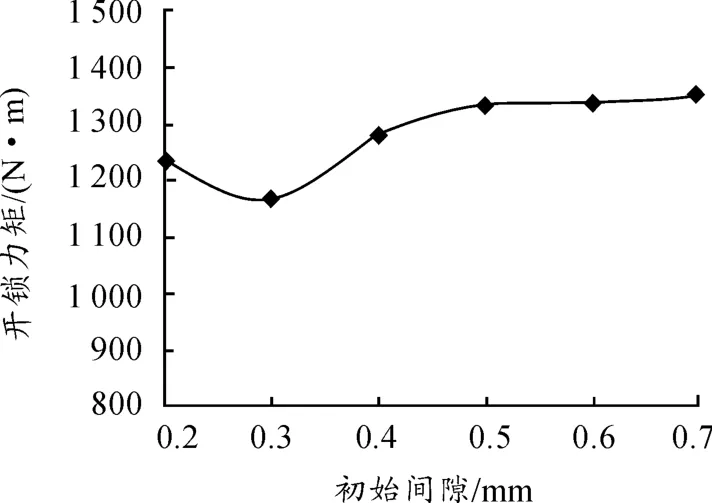
图5 开锁力矩随初始间隙变化趋势
图6是不同摩擦系数下开锁力矩的对比图,可以看出,开锁力矩随摩擦系数的增大而增大。图7 是开锁力矩随摩擦系数变化趋势图,摩擦系数对开锁力的灵敏度约为550 N·m/0.1,因此通过改变零件接触情况而减小开锁力矩是可行的。

图6 不同摩擦系数下开锁力矩对比

图7 开锁力矩随摩擦系数变化趋势
4 结论
通过有限元仿真结果可知:开锁力矩在整个开锁过程中是随时间不断变化的,开锁力矩最大值出现在开锁机构开始开锁时刻,开锁力矩随时间的变化先急剧上升到最大值1 164.6 N·m,然后又急剧下降到963.9 N·m,此过程仅用时0.3 ms,开锁零部件受损大都也发生在这个时候,此峰值对于开锁过程相关零部件寿命分析、工作可靠性分析提供了理论依据。
由仿真对比曲线可以看出:开锁力矩影响因素中,药筒与身管初始间隙对开锁力矩影响幅度比较小,虽然初始间隙在0.3 mm 左右,开锁力矩达到最小值,但综合考虑火炮发射其他方面性能,通过改变初始间隙优化开锁力矩是很有限的。摩擦系数与开锁力矩成线性正相关关系,灵敏度约为550 N·m/0.1,因此通过改善零件接触情况,如给零件镀铬、保持接触面润滑和洁净等方法是可行的[7]。
本文的研究结果可为开锁机构的优化设计、相关零件的寿命计算和工作可靠性分析提供参考。
[1]谭波,侯建.舰炮抽壳机构抽壳过程仿真分析[J].火炮发射与控制学报,2014,35(4):49-52.
[2]陆爽,孙明礼.ANSYS workbench 13.0 有限元分析从入门到精通[M].北京:机械工业出版社,2012:249-253.
[3]卓卫东.应用弹塑性力学[M].2 版.北京:科学出版社,2013:124-130.
[4]刘巨保,罗敏.有限单元法及应用[M].北京:中国电力出版社,2013:142-179.
[5]郑文玮,吴克坚.机械原理[M].7 版.北京:高等教育出版社,2009:357-362.
[6]卓晓琪.火炮抽壳系统的动态弹塑性分析[D].南京:南京理工大学,2002.
[7]卫丰,张光.药筒发射应力和抽壳力的有限元分析[J].爆炸与冲击,2001,21(1):72-75.
