精彩源于“体验”
2015-06-29汪秋莲
汪秋莲
摘要:鉴于初中学生面对数学问题不会思考、无从下手,并且时有产生畏难情绪等现状,通过还原思维初始状态,借助数学典例,师生共同体验思考过程,在操作、观察、方法、情感等深切的体验中,揭开数学神秘的面纱,发展自身思维的能力。
关键词:操作体验;观察体验;方法体验;情感体验;思维发展
时常遇到这样一些情形:这道题目曾经做过、讲过不止一遍,学生再次遇到,依然不会;一道陌生的中等难度的题目学生无从下手;有的学生成绩犹如过山车,一下很高,一下很低……这些现象的背后蕴含着一个相同的本质:学生不会思考问题。对于熟悉的问题,他能够采用正确的解题方法独立地完成,老师不讲他也会;对于陌生的问题,由于思维障碍,无从下手,老师讲了他也不会。如何来改变这一现状呢?如何有效实现《数学课程标准》提出的“数学思考”这一方面的目标呢?下面结合常见的几类数学问题,回顾笔者与学生之间的几段体验。
一、操作体验—将小小纸片动起来
用运动的观点来探究几何图形变化规律的试题已经成为近几年中考及课程改革的热点试题。这类题以运动为载体,集代数与几何的知识于一体,并渗透了分类讨论、转化化归、数形结合、函数方程等重要数学思想,具有开放性、操作性和探究性,因为持续运动将会引发系列变化,所以学生怕做这类问题,觉得难以把握动中之静。有的学生遇到动态问题便会卡住,有的学生遇到动态问题往往漏解,这群孩子有个共性:面对这类问题仅凭想象解题,常常面对试题苦思冥想缺乏动手操作。每逢遇到这类问题,笔者会事先制作一个教具,与学生一起感受、一起体验运动的全过程,以此抓住特殊位置进行分类、抓住不同形状解决问题。
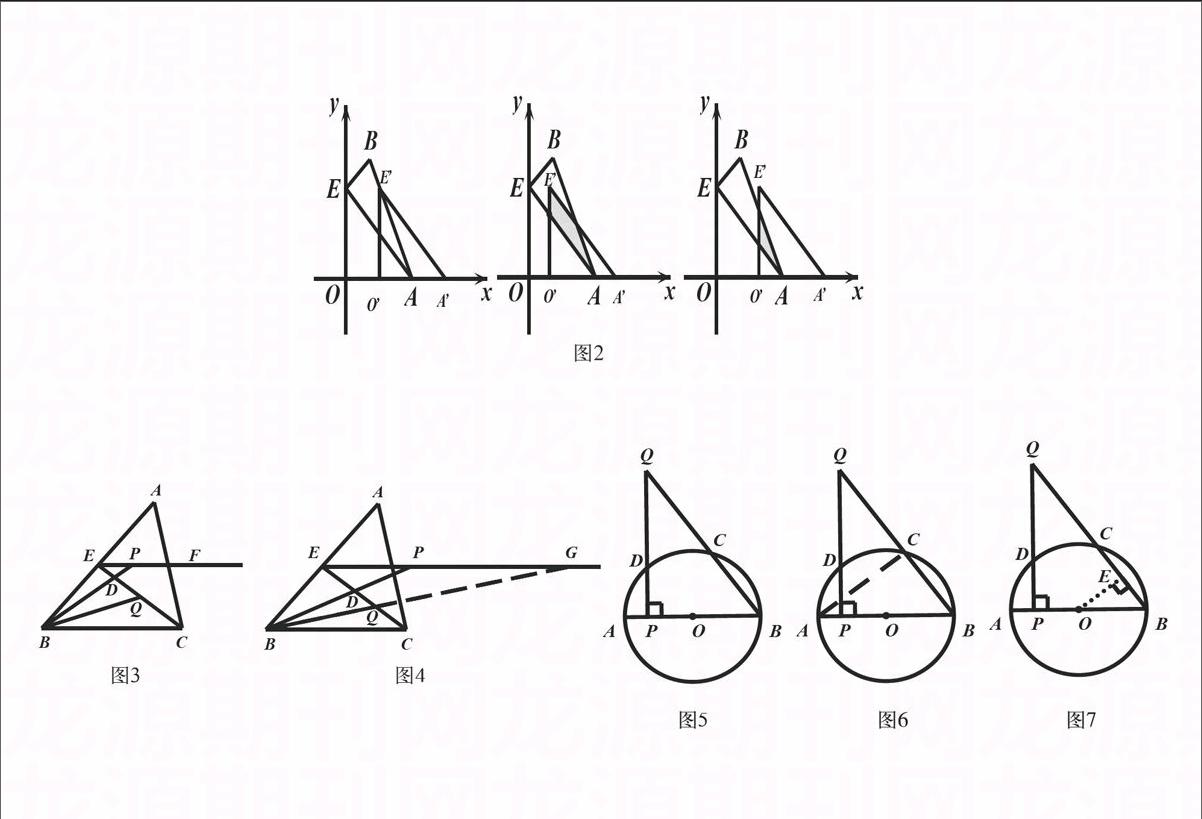
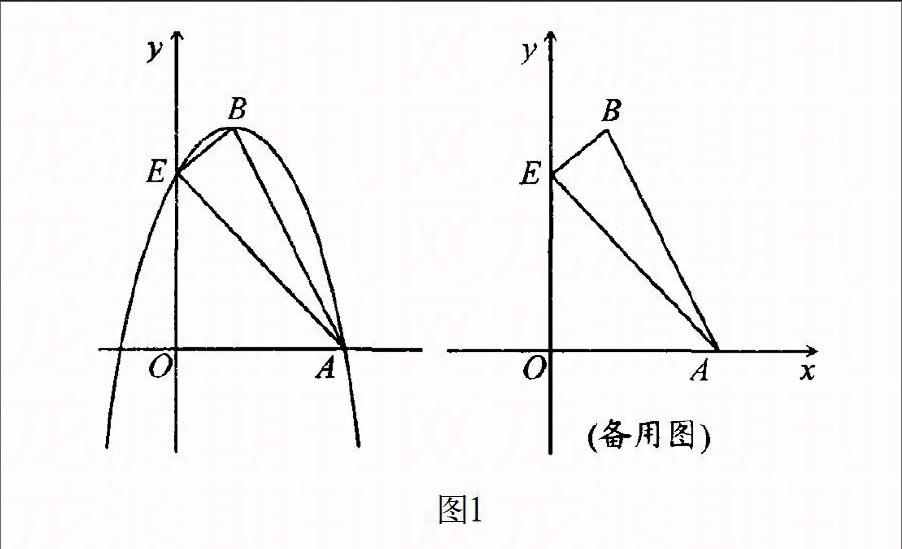
【案例1】如图1,抛物线y=-(x-1)2+4交x正半轴于点A,交y轴于点E,B为抛物线的顶点,连接AB、AE、BE。①求四边形ABEO的面积;②设△AOE沿x轴正方向平移t个单位长度(0 分析:如何准确理解这类问题呢?通过想象获知变化之中的形状并非易事;通过讲评之后获取答案无法有效发展学生能力。于是笔者把拿到这类问题以后的原始思维呈现出来:制作一个与试卷上大小相同的纸片,沿着x轴正方向进行平移,并注意观察重叠部分形状的变化。通过动态演示,学生不难发现:重叠部分的形状有四边形、三角形;然后出示“慢镜头”,提醒学生观察越过哪个地方形状发生改变?(寻找特殊位置),学生亦能发现:当点E,落在AB上;接着,动中求静,画出下列各图(如下页图2),结合图像运用相似三角形的判定与性质等数学知识、运用割补法或面积公式等数学方法、运用数形结合、方程等数学思想解决问题。 【反思】通过经历一个操作的过程,把握行进之中的整个状态,体验问题解决的思维方式,这样,学生在千变万化的动态问题中,能够抓住基本的解题思路:即借助手边的工具(纸片等),通过动态的演练,体验运动的整个过程,抓住运动过程中特殊位置进行讨论并加以解答。通过上述初始思维形态的呈现,意在教给学生以不变(基本的解题思路)应万变(变化的图形、变化的背景、变化的问题)的解题策略。这样,学生通过多次反复的思考和长时间的积累,对于动态问题就能抓住关键,把握要领,学会解题,享受成功,激发学习数学的内驱力和学好数学的自信心。 二、观察体验—将基本模型找出来 意大利科学家伽利略曾说:“大自然用数学的语言讲话,这个语言的字母是:圆、三角形以及其他各种数学形体。”我们的生活中蕴含着丰富的图形,研究数学,我们的学习中充斥着大量的图形,在形态各异的几何图形中,存在着许多基本的图形。在求解几何问题时,往往需要抓住“基本图形”,在复杂的几何图形中辨认、分解出基本图形,或通过添加辅助线补全、构造基本图形;或运用图形变换的思想,将分散的条件集中起来产生基本图形。这是一类几何问题解决的初始想法或基本思路。 【案例2】如图3,在△ABC中,E、F分别是AB、AC的中点,BC=6,CE=5,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q。当EP+BP=18时,则CQ的值为 。 分析:遇到这一问题,不少学生被难倒了,面对多条线,多个点,无法获取有用的信息并加以解决。讲评时,我把自己的思考过程呈现出来:由E、F分别是AB、AC的中点,你能得出什么结论?(中位线及中位线的性质);由EE//BC,BQ平分∠CBP,你又能得出什么结论?(基本图形:平行线+角平分线→等腰三角形);如何构造基本图形呢?(延长BQ交射线EF于点G,如图4所示),这样,不难得到BP=GP,∵EP+BP=18,∴EP+GP=18,即EG=18,要求CQ的值,利用△BCQ~△GEQ的性质即可。学生解答不出的原因主要是,无法将题目已知条件整合推出新的结论,再将结论与其他条件整合获取新的信息;难以从复杂的图形中找出“基本图形”,由陌生的情境转向熟悉的对象。 【反思】通过这题的分析与思考,意在告诉学生首先熟悉数学中的基本图形,不断发展自己的眼力和提高自身的观察能力,这样,面对初次遇见的几何问题,能够快速抽象基本模型,运用已有知识加以解决。 三、方法体验—将基本方法用上来 数学在其漫长的的发展过程中,不仅建立了严密的知识体系,而且形成了一整套行之有效的数学方法和数学思想。美国著名数学教育家波利亚说过:掌握数学意味着要善于解题。所谓“善于解题”,并非陷入“就题论题”的困境,而是进入“以题论法”的境界。只有将数学思想、数学方法理解透彻并会融会贯通时,新看法、新点子自然喷涌而出。所以,在数学教学中,教师应该注重基本方法的传授与基本思想的渗透,发展学生“由已知想可知”、“由未知想需知”的思维方式和思维能力。圆中的计算是作业中错题率较高的一类问题,究其原因,学生解决问题的方向不清晰,解决问题的方法不准确。
【案例3】如图5,AB是⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A、B重合),过点P作AB的垂线交BC的延长线于点Q。若cosB= ,BP=6,AP=1,求QC的长。
分析:引导学生由已知想可知,如见直径想直角,在Rt△BPQ中,cosB= = ,AB=BP+AP=6+1=7等,再由未知想需知,从图形可以看出,CQ=BQ-BC,只要求出BQ与BC的值即可。BQ放置在Rt△BPQ中,BP=6,cosB= ,便可求出BQ的值;BC呢?不妨连接AC,如图6,将BC放置在Rt△ABC中,AB=7,cosB= ,亦能求出BC的值。当然,BC是⊙O的弦,要求弦长,可以先求弦长的一半,因此,过点O作OE⊥BC于点E,如图7,在Rt△BOE中,OB= ,cosB= ,便可求出BE的长,由垂径定理,得出BC=2BE,这样,问题就能得以解决。
【反思】通过这一问题的分析,意在培养学生“由已知想可知”及“由未知想需知”的思考方式和思维能力,并且能够掌握数学问题中常见的解题方法,如求线段的长、求角的度数等都有自身常用的解题思路和解决方法,学生能够在“做”的过程与“思考”的过程中不断积淀,逐步积累运用数学解决问题的经验。
四、情感体验—感受挫败与成功带来的韧性与动力
1.尽管失败,依然呈现碰壁折回
在教学中我们常会有这样的经历:遇到一个陌生的数学问题,第一时间在脑海里浮现的解题思路不一定是正确的,有时需要换个角度、换种思路才能正确地解答出来。数学老师在讲评这一问题时,仅仅展示正确的解题思路,往往回避思维碰壁、如何折回这一过程的呈现。事实上,我们的学生在解题中常常会有碰壁的情形,卡住了,不知所措,思维停滞,最终无法正确解答。所以,笔者觉得在解决问题的过程中碰壁折回这一历程的回溯,对学生而言是弥足珍贵的。教学中,我们无法回避,不能忽略。因此,在数学教学的过程中,我尽量呈现自身初始的思维状态,通过让学生体验完整的思维过程,提高学生的思维能力与解题能力。
2.因为成功,所以说出自我想法
课堂上,我们不仅需要呈现教师原始的思维状态,也有必要提供机会让学生说出自己的想法。有的时候,谈谈自己的想法往往比汇报一个答案更能掀起课堂的高潮。学生智慧的匣子在霎那间打开,猛然发现“我们的孩子非常优秀”。著名教育家陶行知先生曾经提出“六大解放思想”,在我们的数学课堂上,同样需要陶老先生“六大解放思想”的引领,让我们的孩子动起手来,通过眼睛观察,动脑思考,以及由挫败或成功带来的韧性与动力的体验,促使学生掌握基础知识与基本技能,发展抽象思维与推理能力,培养创新意识与实践能力,促进学生在情感、态度与价值观等方面得到发展。
