水深对沙波紊流特性影响的数值分析

董伟良，诸裕良，马殿光，徐俊锋

（1.河海大学港口海岸与近海工程学院，南京210098；2.交通运输部天津水运工程科学研究所工程泥沙交通行业重点实验室，天津300456）

水深对沙波紊流特性影响的数值分析

董伟良1，诸裕良1，马殿光2，徐俊锋2

（1.河海大学港口海岸与近海工程学院，南京210098；2.交通运输部天津水运工程科学研究所工程泥沙交通行业重点实验室，天津300456）

运用FLUENT软件雷诺应力紊流模型（RSM）及SIMPLEC算法，对不同水深下沙波紊流特性进行数值模拟分析，模拟结果与实测结果吻合良好。在此基础上对4种不同相对水深下纵、垂向流速、压强及雷诺切应力分布规律进行研究。研究结果表明∶相对水深较大时紊流特性受沙波地形影响较小，只有近底水体受沙波作用；相对水深较小时整个水体都会受到影响。在沙波尺度不变的条件下，紊流强度一般随水深的增加而减小,不同位置处的沙波紊流特性受水深影响程度及变化规律均不同。最大压强水平位置受水深影响的变化规律与再附点基本一致,可将最大压强作为再附点位置的判断依据。

水深；沙波；紊流特性；数值模拟；水平位置

天然河流和海岸中，沙波运动是冲积河床中泥沙颗粒集体运动的一种主要形式，是阻力计算、河床演变等问题的重要研究内容。然而在河流的不同区域、不同时间，因水深变化，沙波上的水流特性也不尽相同。因此，水深对沙波紊流特性的影响研究是十分有必要的，不仅可以加深对沙波特性及运动规律的认识，同样也有着非常重要的学术意义和工程价值。

近60年内，已有众多国内外学者［1-6］通过水槽实验对沙波上的水流特性进行了研究。Mendoza［7］、Yoon［8］等利用RANS模型研究了沙波上的紊流结构；Stoesser［9］等人利用LES模型模拟了沙波上的水流特性，着重探讨了涡流结构的发展演变过程。然而，以上研究及所得出的结论都仅限于一个或者几个相对水深，没有涉及水深对紊流特性的影响分析。Balachandar［10］在水槽中进行了4组不同水深下的沙波实验，讨论了流速、紊动动能等水力参数的变化规律，但该水槽实验最小水深为3h（h为沙波波高），还没有低于Balachandar［10］在该实验中相对水深d/h=8的条件下沙波作用高度2.5 h，且该水槽实验在沙波尺度不变的条件下，随着水深递增，边壁对水流的影响递增。

基于实际工程问题的需要，本文采用RSM模型对沙波上不同相对水深下的水流特性进行数值模拟，探讨纵、垂向流速、压强和雷诺应力等随水深的变化规律，为研究沙波上水流结构及泥沙运动提供了参考。

1 模型建立

1.1 基本方程

紊流模型采用多方程的雷诺应力（RSM）模型［11］，采用采用一阶迎风格式对方程进行离散，为节省计算时间成本，采用SIMPLEC算法及基于压力的隐式求解器，求解离散方程。

1.2 边界条件

为减少模型网格数及计算时间，同时也能够保证计算的准确性，在进出口选取周期性边界条件，认为水流在一系列沙波上已充分发展，此时流场的边界形状及流场结构存在周期性变化特征，进出口水流特性基本相同。因壁面附近流场梯度较大，对整个紊流场的计算影响显著，因此需要在模型底部边界进行特殊处理。本文采用壁面函数法，即用半经验公式将自由流中的紊流与壁面附件的流动链接起来。计算域的上边界采用对称边界条件∶∂/∂z=0和V=0。

1.3 网格划分

沿水流方向，沙波截面和水流特性具有周期性，本文取一个沙波周期进行数值研究。由于采用壁面函数法，在划分网格时，不需要在壁面区加密，只需要把距壁面第1个内节点布置在对数律成立的区域。对数区的y+＞30～60，流场计算完成后查看y+的值，再进行调整。垂向网格渐变率R=1.1，上疏下密；纵向网格均匀布置，R=1。

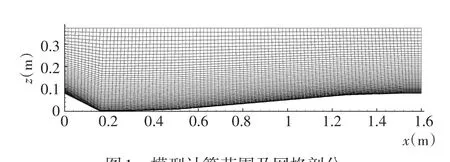
图1 模型计算范围及网格剖分Fig.1Calculation scope and computational grid

2 模型验证

为验证模型的准确性，选取Mielo和Ruiter［2］的实验数据进行验证。沙波波长1.6 m，波高0.08 m，如图1所示，沙波表面泥沙中值粒径D50=1.6 mm。本文选取T6组次实验数据来对模型进行验证，其中流量Q= 0.257 m3/s，水深d=0.334 m，弗汝德数Fr=0.29。

计算模型与实验模型尺寸相同，选取距前一个波峰位置为0.13 m、0.48 m、0.82 m和1.27 m典型断面的计算值与实测值进行比较（见图2）。结果表明，计算值与实测值基本吻合，其中纵向流速不管是分布规律还是数值大小吻合度最高，体现了很好的一致性，但垂向流速、紊动动能和雷诺切应力在波谷附近与实测值存在差异，吻合度越靠近波峰越高。根据Best［4］的实测结果可知，上述差别主要是由于沙波背流面存在较强的漩涡，而RANS模型不能够有效地模拟涡流结构所致，这与Yoon［8］的模拟结果基本一致。整体而言，模型有效地模拟出紊流变化规律，准确地刻画峰值出现的位置和范围，可用于模拟整个沙波上的紊流特性。

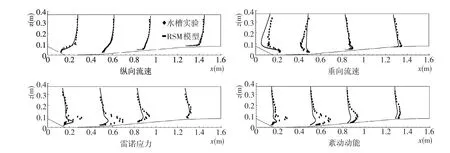
图2 各位置处计算值与实测值的比较Fig.2Comparison of calculated and measured values along the four measurement vertical

3 计算结果和分析

为了方便比较，突出水深对沙波紊流特性的影响，本文在不同水深下所选取的沙波尺度相同，采用Mielo和Ruiter［2］实验时的沙波尺度，沙波波陡h λ=1/20。取平均流速基本相同，共进行4组数值实验，具体参数见表1。选取距前一个波峰位置为0.13 m、0.48 m、0.82 m及1.27 m典型断面进行分析。

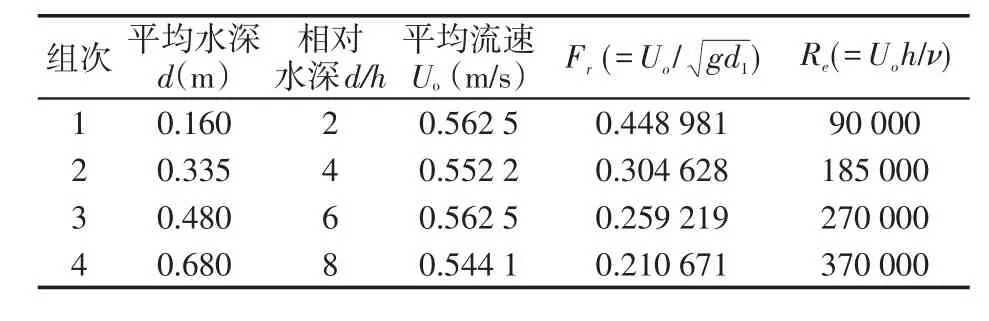
表1 数值模拟实验工况Tab.1Test conditions

3.1纵向流速

图3表明沙波各位置处纵向相对流速受水深影响程度不同：波谷附近0.13和0.48测点受水深影响大于离波谷较远的0.82和1.27测点。研究认为：当水流流经波谷时，因沙波地形作用形成回流区，造成近底流速减小、上部流速增加的特性。根据Stoesser［9］数值模拟结果可知，波谷附近的漩涡结构使得纵向流速分布差别较大；当水流流向波峰时，因远离回流区，且受加速次生流作用，纵向流速分布较为一致，与水深关系并不明显，只有近底存在着细微差别。从图3中还可以看出，不同位置处纵向相对流速受水深影响的变化规律也不同。0.13和0.48测点处，相对水深越小，纵向流速分布越不均匀，呈现近底流速越小、上部流速越大的特性，当相对水深d/h=2时，分布曲线已偏离指数分布规律较多。而在1.27测点处，相对水深越小，纵向流速分布越均匀，上部分布规律基本相同，近底流速随相对水深的减小而增加。

值得注意的是，在所有位置处，相对水深d/h=2的纵向流速分布曲线偏离其他水深较多；而相对水深d/ h=6、8的分布曲线近乎重叠，此时沙波作用范围仅局限于近底部分，上部相对纵向流速分布规律受水深影响较小，与明渠均匀流的水流条件基本一致。

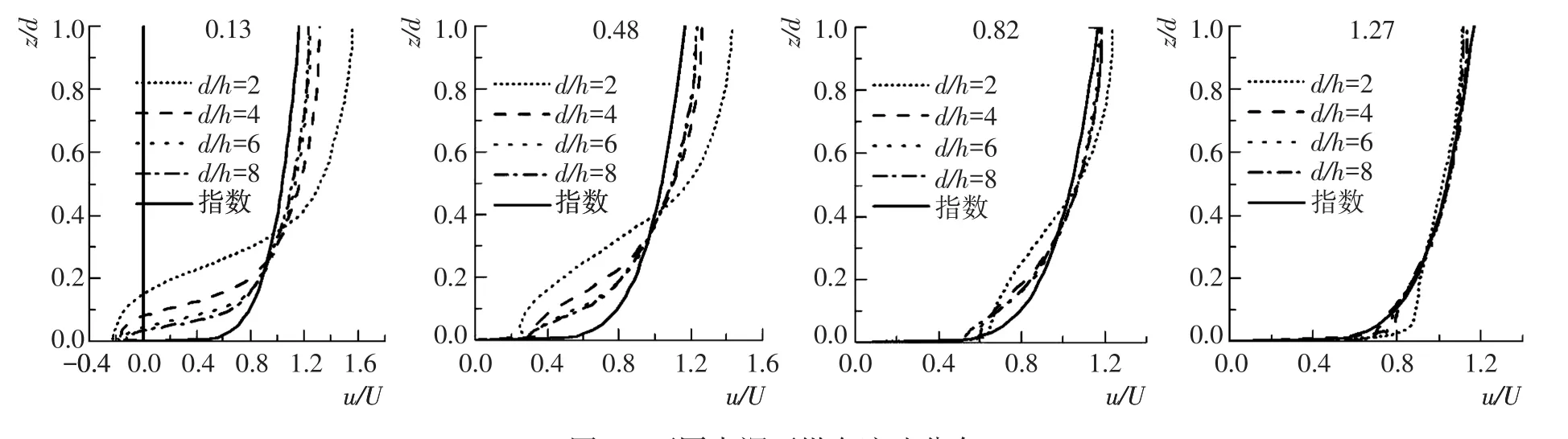
图3 不同水深下纵向流速分布Fig.3Mean streamwise velocity profiles for different depths

3.2 垂向流速

不同水深下相对垂向流速分布如图4所示，正值代表流速向上，负值代表向下。由计算结果可知，相对垂向流速分布存在2种典型断面，不同位置处受水深影响的变化规律也不同：在0.13和0.48测点处，垂向流速从下到上先正后负，整体分布呈“C”型，0.13测点的峰值随着相对水深的增加而增加，当相对水深d/h=2时反而变小；而0.48测点的峰值随着相对水深的增加而增加，相对水深d/h=2的峰值是其他水深的300%左右。0.82和1.27测点的垂向分布曲线基本符合三角形分布，上部呈直线分布，而下部很小，基本可以忽略，峰值的大小和位置随相对水深的增加而增加，且每次增加的量值基本相等。

在平均流速接近的情况下，令

式中：U为平均流速；Q为流量；f（x）为过水断面面积与水平距离的函数。对式（6）微分得

在本文中，式（7）中的f'(x)因沙波尺度不变而在不同水深下相等，U也是如此。所以水深越小，过水断面面积就f(x)越小，∂U/∂x也就越大。

根据质量守恒方程

可知，∂U/∂x增大，-∂V/∂z也增大，即水深越小，-∂V/∂z越大，这与图4中0.82和1.27测点处不同水深下垂向流速分布规律基本一致，同时也说明了模型的正确性。值得注意的是，以上结论均是在平均流速基本接近的情况下得到的，若不等则可以通过上述方法进行计算比较。

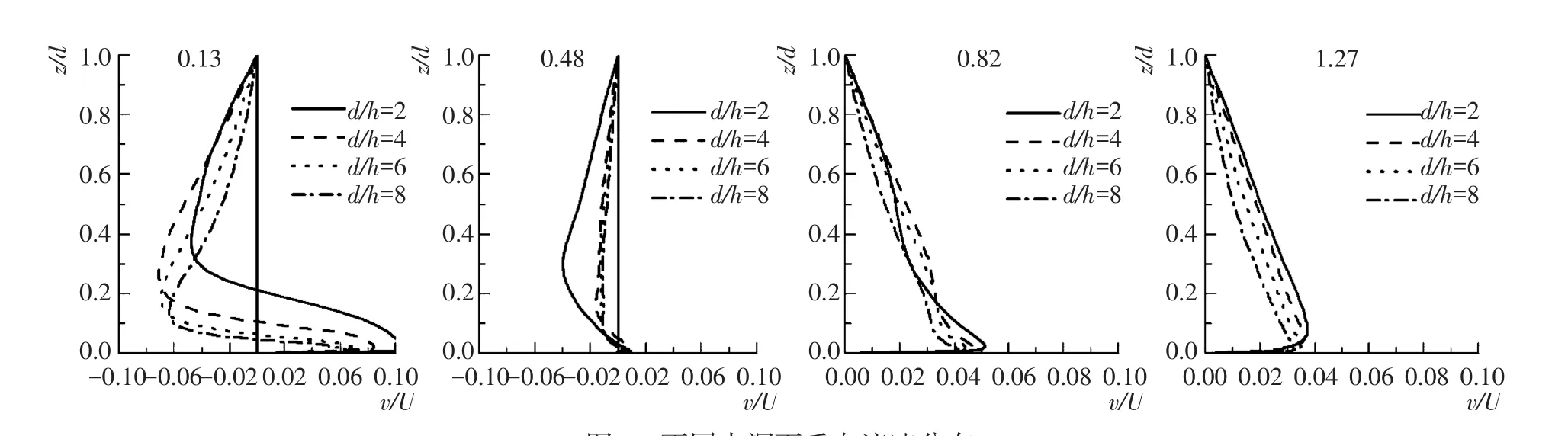
图4 不同水深下垂向流速分布Fig.4Mean vertical velocity profiles for different depths

3.3 压强

压强在迎流面中部存在最大值，并向两侧波峰递减，在波峰处达到最小值。研究认为：水流从波峰俯冲下来，会在迎流面形成较为强烈的冲击，根据牛顿第三运动定律可知，迎流面势必会给水体一个作用力，使得局部压强增大。根据图5实验数据可知，最大压强值随相对水深的增加而减小，即水深越大，水体对沙波的冲击力越小，同样沙波对水体的作用力也越小，这与水深越大沙波阻力越小的结论是一致的。

从图5、6可以看出，最大压强水平位置随着相对水深而变化。在相对水深d/h=2时，xL/h=6.2；当d/h=2～4，最大压强位置xL/h随相对水深的增加而减小；而当相对水深d/h＞4时，xL/h基本保持不变。图6显示，最大值压强位置及变化规律与前人研究的再附点基本一致：d/h=2～4时,计算值介于前人水槽实验数据之间，变化斜率与Nakagawa［12］结果基本一致；虽然当d/h＞4时,本文位置大于Balachandar［10］的实验结果，但两者随水深均基本保持不变。

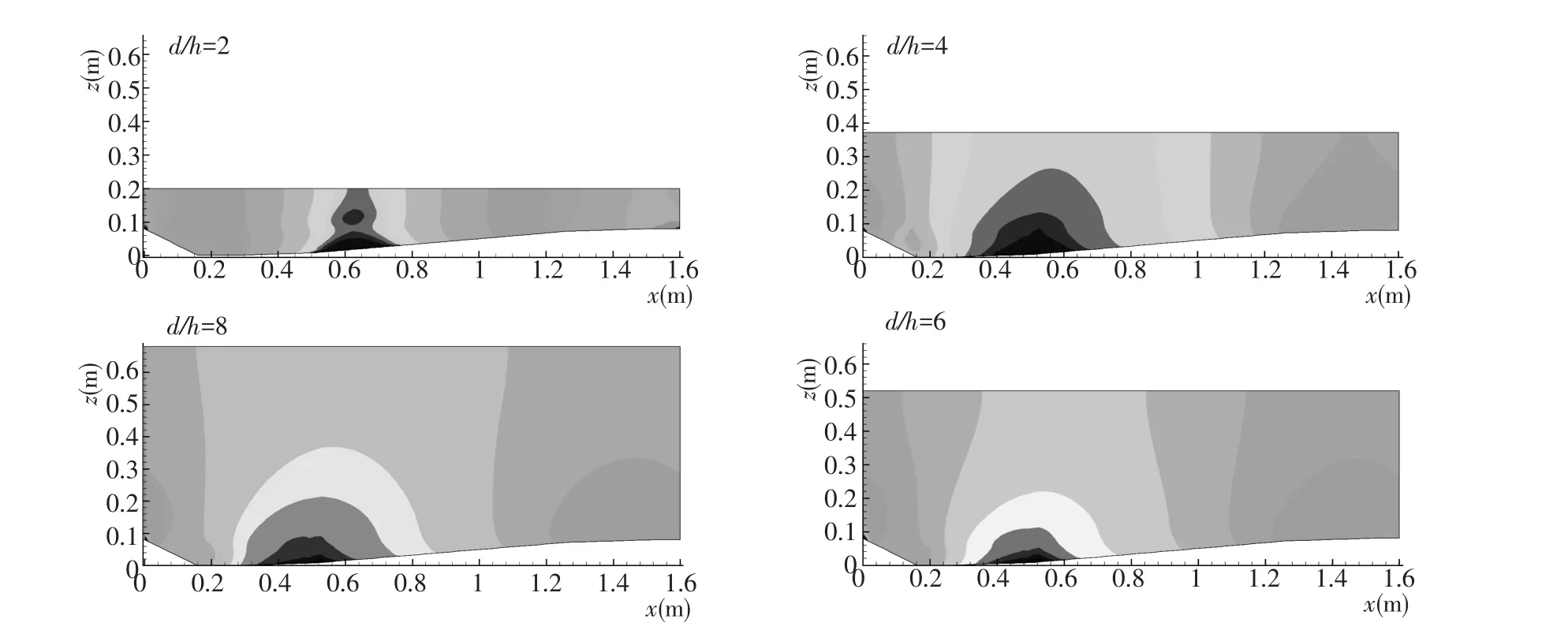
图5 一个沙波周期纵剖面压力分布图Fig.5 Contour plots of pressure distribution of one dune section

3.4 雷诺切应力

图7是不同水深下雷诺应力分布图。0.13、0.48及0.82测点的相对雷诺切应力分布曲线受水深影响较大，峰值的大小和位置随着水深的减小而增大；1.27测点处不同水深下的分布曲线差别不大，峰值位置随相对水深的增加而增加，峰值大小反而减小。研究认为：前3个测点位于波谷附近，因沙波作用高度有限，上部呈直线分布规律，直线段随着相对水深的减小而减小，底部受回流区紊动影响，垂向分布曲线底部存在突出的峰值，越靠近波峰，紊动越小，峰值逐渐消失，分布曲线也更为平滑；1.27测点远离回流区，且迎流面上的加速次生流对水体紊动有抑制作用，水深越小，次生流作用越明显，水体紊动强度也就越低。

从图7中还可以看出：当相对水深d/h=2时，0.13测点的直线段较短，基本可以忽略，此时雷诺切应力的分布规律背离其他水深较多，曲线上部已不再满足直线变化规律，且峰值的大小及范围，均远大于其他情况，此时可认为沙波作用高度已大于水体高度。和相对纵向流速分布规律一样，不同测点处相对水深d/h=6、8的雷诺切应力分布曲线同样几乎重叠，尤其是曲线上部，吻合度更高。通过研究分析可知，水深对相对紊动动能分布规律的影响与相对雷诺切应力基本相同。

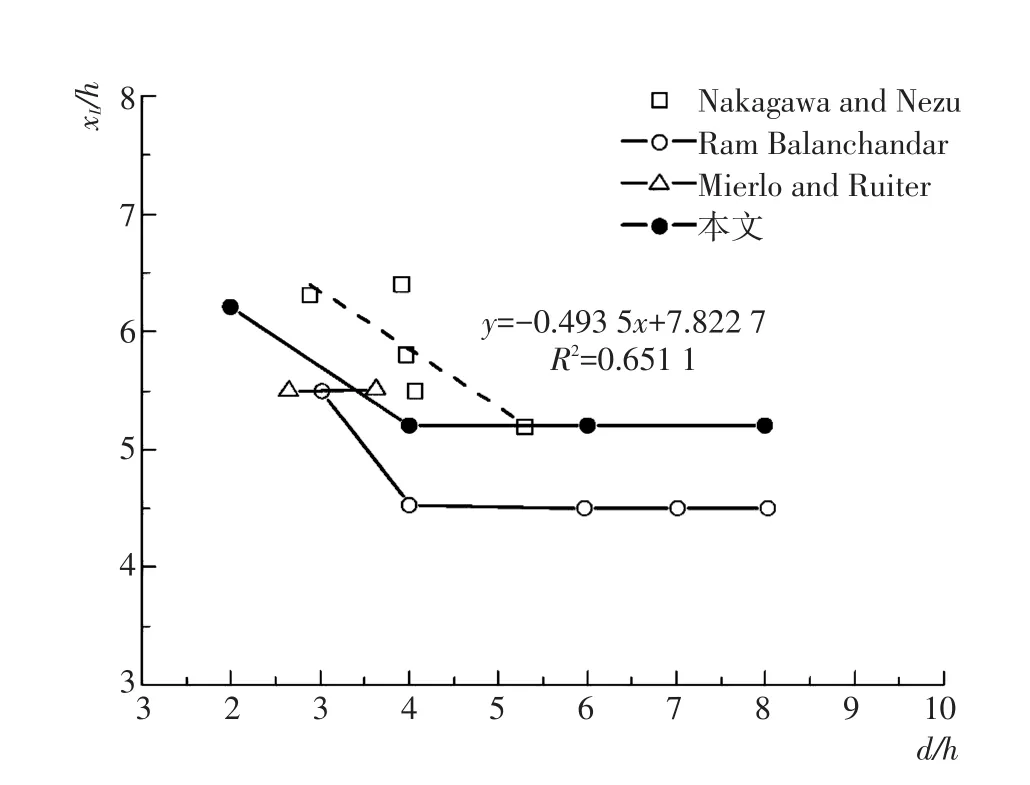
图6 最大压强点位置随水深变化关系图Fig.6Variation of maximum pressure position with depth

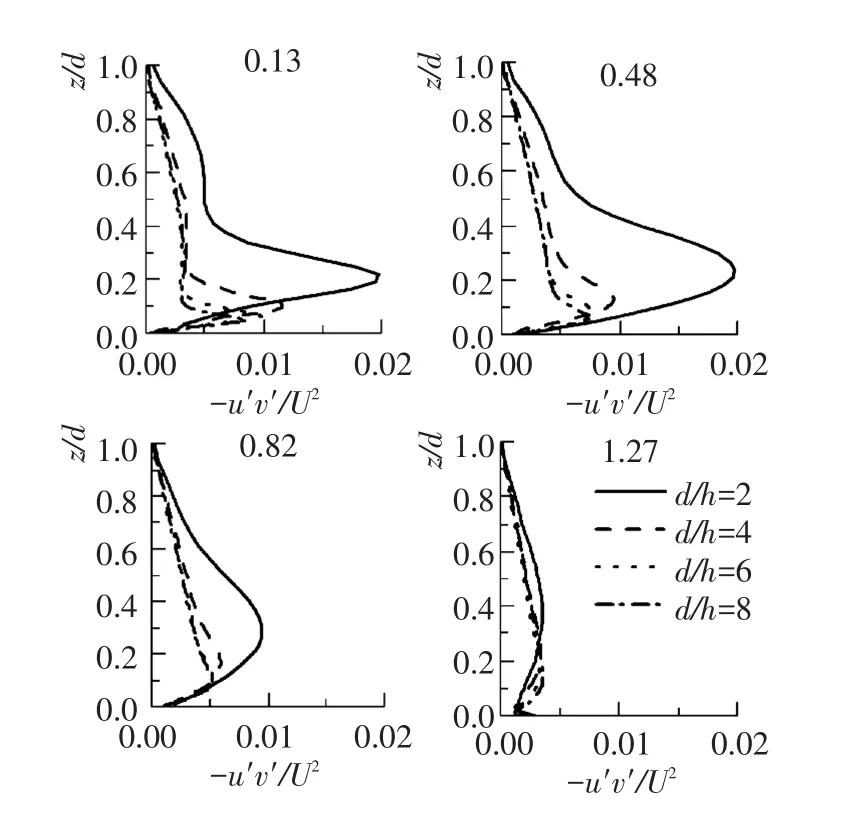
图7 不同水深下雷诺应力分布Fig.7Mean Reynolds shear stress profiles for different depths

4 结论

（1）沙波不同位置处的紊流特性受水深影响程度和变化规律不同。波谷附近的紊流特性主要受回流区紊流和涡流结构影响，相对水深越小紊动强度越高，流速分布越不均匀；波峰附近主要受加速次生流影响，紊流特性则与之相反。

（2）在相对水深较大的条件下，各项水力参数的垂向分布曲线在上部区域基本重合，流态与均匀流接近，水深影响几乎可以忽略，沙波只作用在近底水体，水深越大沙波作用范围也逐渐减小。本文研究认为当相对水深大于6～8时，水力参数垂向分布差别已不是很大。

（3）在相对水深较小（d/h＜4）的条件下，其各项水力参数偏离其他水深较多，这主要是由于沙波作用高度已大于水体，此时紊流特性有别于其他情况，应专门进行研究。

（4）最大压强位置受水深影响的变化规律与再附点基本一致，随着相对水深的减小而增大，当相对水深大于4时其值基本保持不变，可将最大压强作为再附点位置的判断依据，通过研究压强变化来研究再附点。

［1］Bennett S J,Best J L.Mean flow and turbulence structure over fixed,two⁃dimensional dunes∶implications for sediment transport and bedform stability［J］.Sedimentology,1995,42（3）∶491-513.

［2］Mierlo M,De Ruiter J C C.Turbulence measurements above artificial dunes［R］.Delft∶Delft Hydraulics Lab,1988.

［3］Nelson J M,McLean S R,Wolfe S R.Mean flow and turbulence fields over two⁃dimensional bed forms［J］.Water Resources Re⁃search,1993,29（12）∶3 935-3 953.

［4］Best J L.Kinematics,topology and significance of dune⁃related macroturbulence∶some observations from the laboratory and field［J］.Fluvial sedimentology VII,2005（35）∶41-60.

［5］Polatel C.Large⁃scale roughness effect on free⁃surface and bulk flow characteristics in open⁃channel flows［D］.Iowa City∶The Uni⁃versity of Iowa,2006.

［6］唐小南，窦国仁.沙波河床的明渠水流试验研究［J］.水利水运科学研究，1993（1）∶25-31. TANG X N,DOU G R.Experimental study of open channel flow over dunes［J］.Journal of Nanjing Hydraulic Reaearch Institute, 1993（1）∶25-31.

［7］Mendoza C,Wen S H.Investigation of turbulent flow over dunes［J］.Journal of Hydraulic Engineering,1990,116（4）∶459-477.

［8］Yoon J Y,Patel V C.Numerical model of turbulent flow over sand dune［J］.Journal of Hydraulic Engineering,1996,122（1）∶10-18.

［9］Stoesser T,Braun C,Garcia⁃Villalba M,et al.Turbulence structures in flow over two⁃dimensional dunes［J］.Journal of Hydraulic Engineering,2008,134（1）∶42-55.

［10］Balachandar R,Hyun B S,Patel V C.Effect of depth on flow over a fixed dune［J］.Canadian Journal of Civil Engineering,2007, 34（12）∶1 587-1 599.

［11］王福军.CFD软件原理与应用［M］.北京：清华大学出版社，2004.

［12］Nakagawa H,Nezu I.Experimental investigation on turbulent structure of backward facing step flow in an open channel［J］.Jour⁃nal of Hydraulic Research,1997,25（1）∶67-88.

Numerical analysis of water depth effect on turbulence over dunes

DONG Wei⁃liang1,ZHU Yu⁃liang1,MA Dian⁃guang2,XU Jun⁃feng2
（1.College of Harbour,Coastal and Offshore Engineering,Hohai University,Nanjing 210098，China;2.Tianjin Research Institute for Water Transport Engineering，Key Laboratory of Engineering Sediment,Ministry of Transport, Tianjin 300456,China）

The objective of this paper is to study the effect of water depth on the flow over a train of two⁃dimen⁃sional dunes,focused on vertical velocity,Reynolds stress and turbulent kinetic energy distribution.A mathematical model based on the Reynolds⁃Averaged Navier⁃Stokes(RANS)equations,Reynolds stress turbulence(RSM)closure and SIMPLEC algorithm is adopted to describe this complex phenomenon,with simulated results agreed well with measured ones.The numerical results show that turbulence parameters are affected by the relative depth∶the pro⁃files of turbulence parameters collapse onto a single curve in the outer region,with the near⁃bed affected by the dunes at larger depths;dune topography governs the entire water at a shallower depth.It is obvious that the turbu⁃lence intensity decreases with increasing water depth and flow characteristics affected by water depth are different due to positions.Location of maximum pressure affected by depth is consistent with the reattachment point,indicat⁃ing that maximum pressure can be treated as the criterion of reattachment length.

depth;dunes;turbulence;numerical simulation;horizontal position

TV 147；U 617

A

1005-8443（2015）05-0404-05

2015-01-28；

2015-04-08

中央级公益性科研院所基本科研业务费专项资金项目（TKS130105）

董伟良(1990-)，男，江苏省人，硕士研究生，主要从事河流水力学、港口航道等研究。

Biography：DONG Wei⁃liang（1990-）,male,master student.