供应链风险测度的研究进展

刘鹏飞，谢梦洁

（长沙理工大学 交通运输工程学院，湖南 长沙 410004）

供应链管理中存在大量诸如需求不确定、供应不稳定及信息不对称随机因素的影响，可能导致巨大风险，带来利润损失。现实中鉴于风险的广泛性和重要性，供应链的决策目标已不仅仅考虑期望利润最大化，而是建立具有风险度量机制的权衡决策多目标。Hendricks实证表明风险干扰可达到其行业基准33%－40%的利润损失［1］。对供应链中的风险进行准确的测度能更好的支持决策者进行决策。笔者借鉴金融工程中风险测度方法梳理供应链的风险测度研究进展。

金融风险测度工具主要有：均值方差（Mean－Variance，MV）、风险价值（Value at Risk，VaR）、条件风险价值（Conditional Value at Risk，CVaR）。均值方差把期望收益率的波动率定义为风险，应用方差描述收益风险。风险价值允许决策者具体地给定获得一定利润的置信水平。条件风险价值指在给定的时间段内损失的概率超过风险规避水平的损失的条件期望值。

一、均值方差测度供应链的风险研究进展

1.均值方差模型

Markowitz提出均值方差模型，以期望来衡量收益，以方差来衡量风险［2］。假设供应链订货量为q时的期望收益为E P（q［］），收益方差为V P（q［］），给定的方差水平为k2，给定的期望收益水平为ξ，均值方差模型为：

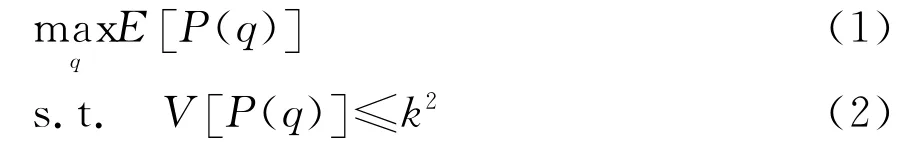
式（1）和式（2）表示在已知给定风险条件下达到期望收益最大。

均值方差模型也可为：

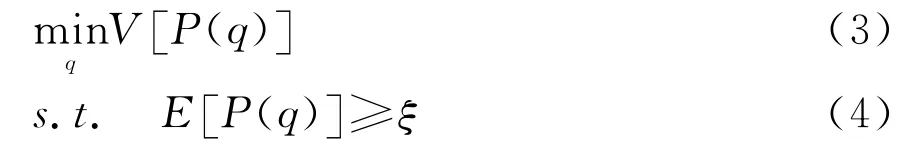
式（3）和式（4）表示在已知给定预期收益条件下使风险最小。

2.运用均值方差研究供应链决策

Lau最早应用均值方差分析报童库存问题［3］。Chen构建均值方差研究单阶段报童问题，未考虑缺货成本，认为风险规避报童的订购量小于风险中性报童的订购量［4］。Wu采用均值方差研究带有缺货成本的风险厌恶报童订购策略，认为缺货成本对报童的订购有显著影响，考虑缺货成本的风险规避报童的订购量不一定比风险中性报童的订购量小，并与不考虑缺货成本的报童模型进行比较研究［5］。Choi采用均值方差研究不同需求分布的报童模型中风险厌恶、风险中性和风险追求行为［6］。Choi采用均值方差研究零售价格外生与内生情形时的报童问题［7］。Ashkan考虑不确定需求受价格、广告支出和服务水平的影响，运用均值方差研究单个风险厌恶供应商与多个竞争风险厌恶零售商组成的供应链决策［8］。梁祺运用均值方差方法研究供应链管理中的组合风险决策问题，实现不同期望收益率水平下多供货源企业的优化组合［9］。季晓芬借鉴均值方差方法刻画供应商的期望成本和组合风险，构建以选择供应商成本和风险最小化为目标的优化决策模型［10］。

3.运用均值方差研究供应链协调策略

叶飞运用均值方差研究具有风险规避特性零售商加盟的供应链回购策略，发现供应商激励风险规避零售商的单位回购价格比激励风险中性零售商的单位回购价格高，单位回购价格随零售商风险规避系数增加而增加［11］。Choi运用均值方差研究供应链合作模型中单一零售商退货给单一供应商策略［12］。Chiu运用均值方差研究风险规避零售商供应链的目标销售回扣策略。回购、退货、回购策略均能完美协调供应链，但决策变量的结果与风险中性下有较大差异［13］。杨渭兰零售商的有效前沿是运用均值方差方法得出，合适的期权通过风险和收益选择［14］。

均值方差通过测量风险较为准确地计算出收益和成本遭受损失的可能性大小。但没有考虑风险发生的概率，对正离差和负离差的平处理，即对期望的向上的影响和不希望的向下的结果同地予以惩罚，对称地处理收益与损失，有违决策者真实的心理感受，并不适合于小概率事件的限制，不能很好地刻画风险。

二、风险价值测度供应链的风险研究进展

1.VaR模型

VaR是在给定的置信度内，所面临风险的大小和可能遭受的最大潜在损失（Smithson，1996）［15］。即

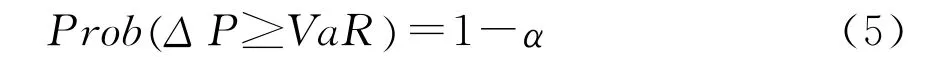
其中，α为给定的概率，即置信水平；ΔP为供应链在特定持有期内的价值损失额；VaR为置信水平α下供应链的风险价值，即可能的损失上限。

2.运用VaR研究供应链决策

Tapiero将VaR引入到库存管理研究中，并指出VaR量化库存风险的方法效果显著［16］。肖辉以最小化损失函数的期望值为目标函数，以规避风险为约束条件，以VaR和CVaR为风险度量，建立具有规避风险的多阶段库存凸随机规划模型［17］。Chiu探讨VaR标准下报童模型的最优决策，并与传统的最优决策进行比较［18］。Özler运用VaR度量方法研究多产品风险规避的报童问题［19］。朱传波针对供应风险，在VaR度量准则下构建具有风险规避特性的零售商的决策目标函数，分析零售商风险规避系数和保留利润构成的风险因子组合对订货策略的影响，分析零售商订货策略对供应链收益与风险的影响［20］。

3.运用VaR研究供应链协调策略

Gan运用VaR研究风险厌恶零售商供应链回购策略的协调性，认为零售商风险与供应商分享，有限的回购量可协调供应链［21］。姚忠运用VaR讨论回购策略对零售商下游风险约束下的供应链协调性，认为回购策略不能获得完美协调，甚至不能获得Pareto改进［22］。史成东采用VaR设计补偿与收益共享、回购组合策略协调制造商是风险中性、分销商和销售商具有下行风险特性的三层供应链［23］；黄松运用收入分享策略协调供应商和零售商具有不同风险态度的供应链［24］。

VaR将预期的风险损失与该损失发生的概率相结合，可使决策者更好地了解不同概率下的风险损失额。但不具备次可加性、凸性，只能衡量置信水平与目标水平之间预期的最大损失，而这种损失不具有代表性。

三、条件风险价值测度供应链的风险研究

1.CVaR模型

CVaR是指在给定的条件和置信水平下，利润低于某个给定VaR水平的平均值（Rockafellar，2000）［25］，即：

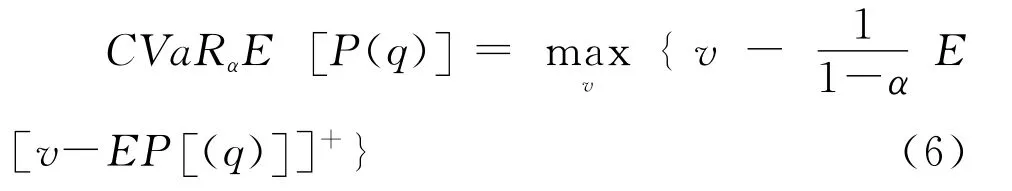
其中，α为风险厌恶因子，即置信水平；v为以VaR为风险度量的决策者期望最大化为订货量q时的期望收益。

2.运用CVaR研究供应链决策

周艳菊运用CVaR研究多产品订货决策，将模型转换为线性规划问题求解［26］。Choi运用CVaR风险度量讨论多产品风险规避的报童问题［27］。Chen仅考虑零售商存在残值处理而不考虑缺货惩罚时CVaR度量准则下报童的最优订购量［28］。许明辉以CVaR研究缺货惩罚和零售商风险厌恶对订购量的影响，认为零售商最优订购量与缺货惩罚单调递增，与零售商风险厌恶程度却不一定具有单调性［29］。Cheng以CVaR作为零售商的风险度量研究双层报童模型［30］。程露将双层规划模型转换成单层规划模型求解研究双层报童模型［31］。安智宇研究供应商具有随机违约与需求下的订货决策［32］。李建斌考虑单个供应商和两个零售商的供应链系统，采用CVaR刻画决策者的风险特性［33］。Chen运用CVaR研究需求依赖价格的报童问题，分析风险厌恶对最优价格和订货批量决策的影响［34］。马利军考虑随机需求依赖价格的供应链合作博弈问题，风险厌恶零售商以CVaR衡量，发现加法需求模式下Nash博弈问题存在均衡的最优批发价格、零售价格和订货量［35］。叶飞研究随机需求对价格和时间敏感的两个风险规避零售商，以CVaR度量风险探讨Bertrand及Stackelberg双寡头博弈下，风险规避对自身和对方的定价、承诺交货期及期望效用的影响［36］。禹海波运用CVaR研究随机需求依赖销售努力时风险厌恶程度对系统决策和利润的影响，认为风险厌恶降低系统利润水平，但不一定导致努力水平和订货批量的减小［37］。李绩才以CVaR作为风险度量准则建立风险厌恶型零售商广告投入与订货量联合决策的随机模型，揭示风险厌恶程度、需求不确定性以及商品本身特性对零售商最优广告投入和订货量的影响［38］。罗春林运用CVaR度量零售商风险厌恶，研究风险厌恶不确定情形下供应链的定价与订货策略［39］。于辉引入CVaR刻画突发事件下的应急目标，建立供应链应急援助的决策模型［40］。Gotoh考虑决策者在少订货赢利不够与多订货滞销之间的平衡，以期望利润与CVaR的加权平均为准则研究给定外部环境下的订货策略［41］。柳键考虑决策者风险厌恶对外部环境决策者的影响，以利润－CVaR准则研究风险厌恶零售商的订货策略及风险中性供应商的定价策略［42］。钟昌宝构建以CVaR、利润、客户满意度为目标的分销网络设计多目标优化模型，实现分销网络风险损失、利润和客户满意度目标之间的均衡［43］。

3.运用CVaR研究供应链协调策略

Yang运用CVaR研究风险中性供应商和风险厌恶分销商组成的供应链回购、收益共享策略，证明回购、收益共享策略可以达到协调［44］。罗春林以CVaR度量零售商风险厌恶，供应商提出回购策略以减轻零售商风险顾虑，结果表明当零售商风险厌恶超过一定程度，回购策略不能实现供应链协调，当回购策略可以实现协调供应链时，供应链的协调利益可以在供应商和零售商之间进行任意的分配［45］。邱若臻运用CVaR给出能够完全协调风险偏好零售商和风险中性供应商的供应链回购策略［46］。闻卉运CVaR研究风险规避零售商与供应商的供应链回购协调策略［47］。于春云运用CVaR研究风险规避零售商与供应商供应链回购策略的协调性，认为供应商与零售商的风险规避水平越接近，越有利于长期稳定合作；供应商与零售商的风险规避水平差距越大，合作越不稳定，甚至不能实现完美协调［48］。Hsieh利用CVaR度量零售商风险，研究单一制造商及两个风险规避零售商组成的供应链回购策略［49］。Demirag运用CVaR研究随机需求依赖价格的回扣策略［50］。林强认为风险规避零售商与供应商存在随机弹性需求［51］。叶飞在Stackelberg博弈情形下研究收益共享协调策略［52］。张新鑫构建顾客策略行为下基于CVaR风险度量准则及收益共享契约的供应链决策模型，探讨收益共享契约的协调机制和利润的分配机制［53］。

CVaR是一致性的风险度量工具，但只关注利润低于某个给定水平的利润平均值，忽略利润高于该水平的情况，显得过于保守。

四、研究展望

（1）利润－CVaR既反映追求高利润的愿望，又反映潜在风险的控制，利润－CVaR综合度量供应链的风险是研究趋势。

（2）多成员、多阶段、多周期的供应链风险决策运用利润－CVaR综合度量是研究趋势。

（3）风险供应链协调策略运用利润－CVaR综合度量是研究趋势。

［1］Hendricks K B，Singhal V R.An empirical analysis of the effect of supply chain disruptions on long－run stock price performance and equity risk of the firm［J］.Production and Operations Management，2005，14（1）：35－52.

［2］Markowitz H M.Portfolio selection：efficient diversification of investment［M］.Yale University Press，New Haven，CT，1959.

［3］Lau H S.The newsboy problem under alternative optimization objectives［J］.Journal of the Operational Research Society，1980，31：525–535.

［4］Chen F，Federgruen A.Mean－variance analysis of basic inventory models［M］.New York：Columbia University，2000.

［5］Wu J，Li J，Wang S Y，et al.Mean–variance analysis of the newsvendor model with stock out cost［J］.Omega，2009，37（2）：724－730.

［6］Choi T M，Li D，Yan H.Mean－variance analysis for the newsvendor problem［J］.IEEE Transactions on Systems，Man and Cybernetics：Part A，2007.

［7］Choi T M，Chiu C H.Mean－downside－risk and mean－variance newsvendor models：Implications for sus－tainable fashion retailing ［J］.International Journal of Production Economics，2012，135（2）：552－560.

［8］Ashkan H，Ahmad M，Seyed J.Strategic and tactical design of competing decentralized supply chain networks with risk－averse participants for markets with uncertain Demand［J］.Mathematical Problems in Engineering，2011，35（4）：1－27.

［9］梁祺，叶孝明，王影.供应链管理中的组合风险决策［J］.统计与决策，2006（1）：151－153.

［10］季晓芬，陈炜，蔡丽玲.基于 Markowitz风险和效用理论的服装供应商决策模型［J］.纺织学报，2011，32（11）：137－142.

［11］叶飞，李怡娜.具有风险规避者加盟的供应链协作回购契约机制研究［J］.工业工程与管理，2006，11（2）：1－4.

［12］Choi T M，Li D，Yan H.Mean－variance of a single supplier and retailer supply chain under a return policy［J］.European J of Operational Research，2008，184（1）：356－376.

［13］Chiu C H，Choi T M，Li X.Supply chain coordination with risk sensitive retailer under target sales rebate［J］.Automatic，2011，47（6）：1617－1625.

［14］杨渭兰，王军.基于期权的供应链协调契约风险收益研究［J］.物流技术，2015（3）：104－107.

［15］Smithson C，Minton L.Value at Risk［J］.Risk，1996，9（1）：25－27.

［16］Tapiero C S.Value at risk and inventory control［J］.European Journal of Operational Research，2005，163（2）：769－775.

［17］肖辉.规避风险的多阶段最优库存研究［J］.经济数学，2012，29（3）：27－31.

［18］Chiu C H，Choi T M.Optimal pricing and stocking decisions for newsvendor problem with value－at－risk consideration［J］.Transactions on System，2010，40（5）：1116－1119.

［19］Özler A，Tan B，Karaesmen F.Multi－product newsvendor problem with value－at－risk considerations［J］.International Journal of Production Economics，2009，117（2）：244－255.

［20］朱传波，季建华，包兴.供应风险规避下基于VaR的零售商订货策略［J］.系统管理学报，2014，23（6）：861－866.

［21］Gan X H，Sethi S P，Yan H M.Channel coordination with a risk－neutral supplier and a downside－risk－averse retailer［J］.Production and Operations Manage－ment，2005，14（1）：80 －89.

［22］姚忠.风险约束下退货合同对供应链的协调性分析［J］.管理科学学报，2008，11（3）：96－105.

［23］史成东，陈菊红.Downside－Risk测度下三层供应链协调契约研究［J］.中国管理科学，2010，18（1）：90－94.

［24］黄松，杨超，杨珺考虑成员风险态度和VaR约束时的供应链协调模型［J］.管理工程学报，2011，25（2）：136－141.

［25］Rockafellar R T，Uryasev S.Optimization of conditional value－at－risk［J］.Journal of Risk，2000，2：21－41.

［26］周艳菊，邱菀华，王宗润.基于CVaR约束的多产品订货风险决策模型［J］.中国管理科学，2006，14（）5：62－67.

［27］Choi S Y，Ruszczynski A，Zhao Y.A multiproduct risk－averse newsvendor with law－invariant coherent measures of risk ［J］.Operations Research，2011，59（2）：346－364.

［28］Chen X，Sim M，Levi D S，et al.Risk aversion in inventory management［J］.Operations Research，2007，55（5）：828－842.

［29］许明辉，于刚，张汉勤.带有缺货惩罚的报童模型中的CVaR研究［J］.系统工程理论与实践，2006，26（10）：1－8.

［30］Cheng L，Wan Z，Wang G.Bilevel newsvendor models considering retailer with CVaR objective［J］.Computers and Industrial Engineering，2009，57（1）：310－318.

［31］程露，万仲平，侯阔林.CVaR准则下的双层报童问题模型研究［J］.运筹学学报，2008，12（4）：83－93.

［32］安智宇，周晶.考虑供应商违约风险的CVaR最优订货模型［J］.中国管理科学，2009，17（2）：66－70.

［33］李建斌，张汉勤，于刚.带有市场搜索的供应链最优策略的分析与比较［J］.系统工程理论与实践，2009，29（10）：53－62.

［34］Chen Y，Xu M，Zhang Z.Technical note－A risk－averse newsvendor model under the CVaR criterion［J］.Operations Research，2009，57（4）：1040－1044.

［35］马利军，刘芳梅，林旭东.加法需求模式下具有风险厌恶零售商的供应链合作博弈分析［J］.系统管理学报，2011，20（4）：398－405.

［36］叶飞，李彦平，李怡娜.风险规避的零售商定价与交货期竞争决策模型［J］.工业工程与管理，2012，17（3）：1－8.

［37］禹海波，杨传平.在供应链角度下风险厌恶对需求依赖销售努力报童问题的影响［J］.中国市场，2011，（6）：7－9.

［38］李绩才，周永务，钟远光.基于CVaR准则的Newsboy型商品最优广告费用与订货策略［J］.系统工程理论实践，2012，32（4）：776－783.

［39］罗春林，柳键，李杰.风险厌恶因子不确定的二阶供应链定价与订货策略［J］.控制与决策，2011，26（1）：141－144.

［40］于辉，邓亮，孙彩虹.供应链应急援助的CVaR模型［J］.管理科学学报，2011，14（6）：68－75.

［41］Gotoh J Y，Seshadri S.Hedging inventory risk through market instruments［J］.Manufacturing ＆Service Operations Management，2005，7（2）：103－120.

［42］柳键，罗春林.利润－CVaR准则下的二级供应链定价与订货策略研究［J］.控制与决策，2010，25（1）：130－133.

［43］钟昌宝，魏晓平，聂茂林.考虑DNCVaR－利润－客户满意度的分销网络设计多目标优化模型［J］.系统工程理论实践，2012，32（10）：2154－2162.

［44］Yang L，Xu M H，Yu G.Supply chain coordination with CVaR criterion［J］.Asia－Pacific Journal of Operational Research，2009，26 （1）：135－160.

［45］罗春林.基于回购契约的风险厌恶零售商的供应链协调［J］.经济数学，2010，27（4）：8－16.

［46］邱若臻，黄小原.基于条件风险值准则的供应链回购契约协调策略［J］.运筹与管理，2011，20（4）：10－17.

［47］闻卉，曹晓刚，黎继子.基于CVaR的供应链回购策略优化与协调研究［J］.系统工程学报，2013，28（2）：211－217.

［48］于春云，赵希男，彭艳东，等.基于条件风险值理论的供应链优化与协调模型研究［J］.中国管理科学，2007，15（3）：31－39.

［49］Hsieh C，Lu Y.Manufacturer’s return policy in a two－stage supply chain with two risk－averse retailers and random ［J］.European Journal of Operational Research，2010，207（1）：514－523.

［50］Demirag C O，Chen Y H，Li J B.Customer and retailer rebates under risk aversion ［J］.International Journal of Production Economics，2011，133（2）：736－750.

［51］林强，叶飞，陈晓明.随机弹性需求条件下基于CVaR与收益共享契约的供应链决策模型［J］.系统工程理论实践，2011，31（12）：2296－2307.

［52］叶飞，林强.风险规避型供应链的收益共享机制研究［J］.管理工程学报，2012，26（1）：113－118.

［53］张新鑫，申成霖，侯文华.考虑顾客行为和成员风险规避性的供应链收益共享契约的设计与协调［J］.预测，2015，34（1）：70－76.