一个新的下丘脑-胰岛轴血糖调解系统激素分泌的非线性动力学模型

王 颖，刘 雯，佟 倜

（1.吉林大学数学学院，吉林长春130012；

2.吉林大学第二医院胸外科，吉林长春130041）

一个新的下丘脑-胰岛轴血糖调解系统激素分泌的非线性动力学模型

王 颖1，刘 雯1，佟 倜2

（1.吉林大学数学学院，吉林长春130012；

2.吉林大学第二医院胸外科，吉林长春130041）

提出了一个新的下丘脑-胰岛轴血糖调节系统激素分泌的非线性动力学模型.该模型能够合理地描述健康人群胰岛素、胰升糖素对血糖的调节作用以及这些激素随时间演化的动力学规律.仿真模拟口服葡萄糖耐量实验（OGTT）结果表明，该模型是一个更加符合人体生理实际的血糖调节模型.

下丘脑-胰岛轴；血糖调节；胰岛素；胰升糖素；OGTT；非线性动力学模型

文献［1］首次建立了健康人下丘脑-胰岛轴（Hypothalamus-pancreatic island axis，HPA）内分泌激素对血糖调节的非线性动力学模型.该模型详细描述了系统内胰岛素（Insulin，INS）的分泌以及胰岛素调控血糖（blood glucose，GLU）的动力学行为，仿真模拟糖负荷状态表明，该模型输出的数据与健康人实际口服葡萄糖耐量实验（Oral glucose tolerance test，OGTT）结果相符合，说明这是一个有效的模型.但上述模型是在简化系统参与因子，只选取主要影响因素而没有全面考虑其他激素对系统影响的前提下建立的.因此，有必要对原有模型进行改进，建立更符合人体生理实际分泌代谢的新模型.由生理学可知，胰岛素是调节血糖和维持血糖稳定最重要的激素，此外，血糖的调节过程还受其他激素的作用，例如胰升糖素（Glucagon，GC）、肾上腺激素等也都实际参与了对血糖的调节.人体血糖的调节是在下丘脑-胰岛轴系统内完成的，这是一个及其复杂的过程［2］，除了有脑神经递质和胰岛素参与外还有与胰岛素相拮抗的激素——胰升糖素以及其他激素的参与.糖负荷状态下胰岛在血糖和下丘脑神经递质乙酰胆碱（Acetylcholine，ACh）的双重刺激下，使胰岛B细胞分泌大量胰岛素来加速血糖代谢和储存，使血糖水平降低，同时高浓度的胰岛素又通过外周血通路下调胰岛A细胞的分泌，使胰升糖素分泌减少，而低血糖时又会上调胰岛A细胞分泌胰升糖素，并通过外周血液循环进入肝脏刺激肝糖原向血液释放葡萄糖使血糖升高，防止低血糖发生，从而保持人体血糖平稳［3］.因此，建立了新的加入胰升糖素影响的下丘脑-胰岛轴内分泌激素对血糖调节的非线性动力学模型.

1 新模型

根据下丘脑-胰岛轴血糖调节规律建立的新模型各参量关系框图如图1所示.框图中表示了各调节激素之间的相互作用和物质流向，并加进了胰腺组织中的胰岛A细胞分泌胰升糖素对血糖影响的通路.其中：⊕和⊖分别表示激活和抑制作用，是复杂的酶促反应过程，遵从Michaelis-Menten酶促反应定律的推广形式；双箭头⇒表示代谢清除；实线框内的是血液中可测到的激素或葡萄糖含量；虚线框中是细胞或组织器官.

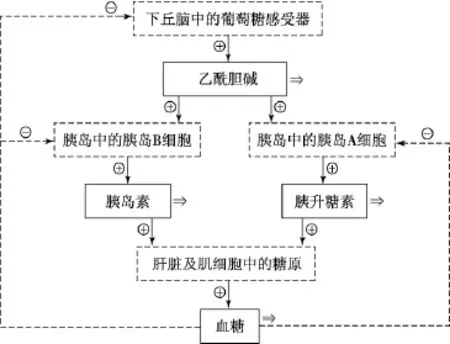
图1 新模型下丘脑-胰岛轴血糖调节框图

考虑到激素分泌都具有饱和性、不能无限制增大的特点，因此把激素分泌的产生项用分数形式表示，并把分子和分母都写成了多项式的形式，根据血糖调节框图新建立的非线性动力学方程如下：

其中：x1，x2，x3，x4分别为血液中乙酰胆碱浓度、胰岛素浓度、胰升糖素浓度和葡萄糖浓度，单位分别是nmol／L，μIU／mL，pg／mL，mg／dL；xi（0）＝x0i（i＝1，2，3，4）表示x1，x2，x3，x4糖负荷开始的初始浓度值；t为时间，单位是min；ai（i＝0，1，…，20）是常系数；bj（j＝1，2，3，4）为激素或血糖x1，x2，x3，x4的代谢清除系数（或降解系数），均为正数.方程中各正项为各激素产生项，负项为代谢清除项.新增加的方程（1c）表示了胰升糖素和其他激素相互作用的动力学关系，方程（1d）为修改后的方程，增加了a20x3项，表示胰升糖素对血糖的影响.

上述方程中待定系数ai（i＝0，1，…，20），bj（j＝1，2，3，4）共24个，且不存在一组完整的实验数据或曲线，因此不能用一般方法（如阻尼二乘法和线性回归法等）来求解这些系数，只能用试验法，经过上千次的反复试验确定出了一组较理想且符合要求的数据，最后得到了具有确定系数的动力学方程：

2 方程的解

依据现有数学理论分析可知方程2没有解析解，只能利用计算机求出方程的数值解，因此采用四阶Runge-Kutta变步长数值积分法并用Maple软件编程求解，即对满足初始条件的微分方程组（2a）—（2d）的一组数据进行求解计算，得到了方程的数值解（见图2）.

图2 模型输出的健康人血浆葡萄糖、胰岛素、胰高血糖素浓度随时间的变化曲线（动态数值解）

3 结果分析

由图2可以看出健康人糖负荷后，人体血糖浓度开始快速升高，在40min后达到最大值，随后开始下降，180min后血糖水平恢复到接近初始状态值，与此同时胰岛素浓度也随血糖浓度平行变化也在40min左右达到最大值，随后开始逐渐下降，180min后恢复到接近初始状态值.而胰升糖素浓度从糖负荷开始缓慢下降但降幅较小，50min达到最小值，随后开始逐渐上升，180min回到初始值附近.这一结果与文献［4-5］报道的正常人口服葡萄糖耐量实验（OGTT）给出的数据相符合（见表1）.

表1 正常人口服葡萄糖耐量（OGTT）实验值与模型计算值

总体来看，上述模型较全面地考虑了各激素之间的相互调节作用，并以实验为依据，求得模型方程的解与实验值符合得较好并符合生理学解释，能够较好地反映健康人胰岛素、胰升糖素激素分泌和对血糖的调节规律，说明这个新模型是合理的.

4 结语及展望

早在20世纪80年代就有人尝试用非线性动力学模型来研究人体复杂生理系统，特别是对内分泌系统中激素的周期性节律变化做了深入地研究［6－7］，这种通过建立人体内分泌激素调节的数学模型将非线性动力学理论应用于人体生理调节系统，并通过计算机仿真来模拟人体激素释放的动态过程的研究又成为近期关注的热点［8－9］.需要说明的是我们在研究该模型方程的过程中发现模型的解具有相当大的不稳定性，在特定条件下会出现振荡，这预示该模型可能还存在周期振荡解，也就是说在血糖调节过程中激素应该是以脉冲方式分泌释放的，近期有关对胰岛素分泌方式的研究［10］也支持我们的这一观点，尽管我们对胰岛素这种脉冲式分泌调节的生理学意义还不十分清楚，但胰岛素的这种脉冲分泌方式有可能会成为今后预测和诊断2型糖尿病的一个重要因子.这提示我们从非线性动力学模型出发探究血糖调节过程中胰岛素脉冲分泌机制的规律应是今后研究的重点.

［1］ 王颖，孙迎春，佟倜.下丘脑-胰岛轴血糖调节的非线性动力学模型［J］.东北师大学报：自然科学版，2010，42（1）：133-136.

［2］ 施密特，特夫斯.人体生理学［M］.北京：科学出版社，1991：759-760.

［3］ 姚泰.生理学［M］.北京：人民卫生出版社，2002：401-405.

［4］ 胡绍文，郭瑞林，童光焕.实用糖尿病学［M］.北京：人民军医出版社，2003：82-83.

［5］ 陈超凤，沈洁，陈志，等.不同糖代谢状态人群OGTT条件下血浆GIP及GC水平变化［J］.中国现代医学杂志，2012，22（36）：30-34.

［6］ BERGMAN RN，IDER YZ，BOWDEN CR，et al.Quantitalive estimation of insulin sensitivity［J］.Am J Physiol，1979，236：667-677.

［7］ LIU BINGZHENG，ZHAO ZHENYE，CHEN LIANSONG.A mathemarieal model of reulition system of the seererion of glueoeortleo：ds［J］.J Biol Phys，1990，17：221-233.

［8］ 赵泓扬，刘立生，韩庆邦.一种基于HHT和神经网络的智能轴承状态监控系统［J］.东北师大学报：自然科学版，2013，45（2）：73-78.

［9］ 付军，吴喆，朱宏.一类非线性周期种群系统的最优收获控制［J］.东北师大学报：自然科学版，2013，45（2）：5-9.

［10］ 于浩泳，吴海娅，贾伟平.胰岛素脉冲样分泌的机制及临床意义［J］.中华内分泌代谢杂志，2005，21（3）：285-287.

A new non-linear dynamics model of the pulsatile secretion of blood glucose regulation by hypothalamus-pancreatic island axis

WANG Ying1，LIU Wen1，TONG Ti2
（1.School of Mathematics，Jilin University，Changchun 130012，China；2.Department of Thoracic Surgery，No.2Hospital of Jilin University，Changchun 130041，China）

The investigation put forward a new hormone secretion nonlinear dynamic model of hypothalamus-islet blood glucose regulation system.The result of the model can reasonably describe the regulating effect of blood glucose of healthy population's insulin and glucagon.It can also obtain the kinetics law of endocrine hormone evolving with time.The simulated oral glucose tolerance test（OGTT）results show that the blood glucose accommodation model is a better one which is more conformed to physiological facts of human.

hypothalamus-pancreatic island axis；blood glucose regulation；insulin；glucagon；OGTT；non-linear dynamics model

O 175.14；Q 45 ［学科代码］ 110·5110

A

（责任编辑：石绍庆）

1000-1832（2015）03-0064-04

10.16163／j.cnki.22-1123／n.2015.03.014

2014-09-09

吉林省科技发展计划项目（20030543-3，20080734）.

王颖（1962—），女，教授，博士研究生导师，主要从事医学非线性动力学系统研究；佟倜（1962—），男，教授，博士研究生导师，主要从事胸外科临床及基础医学研究.