Gierer-Meinhardt模型的稳定分析和时空分歧

李海侠

（宝鸡文理学院数学与信息科学学院，陕西宝鸡721013）

Gierer-Meinhardt模型的稳定分析和时空分歧

李海侠

（宝鸡文理学院数学与信息科学学院，陕西宝鸡721013）

在齐次Neumann边界条件下，讨论了Gierer-Meinhardt模型的稳态分歧和Hopf分歧.给出了正常数解的稳定性.利用分歧理论、空间分解和隐函数定理研究了系统的单重和二重分歧，并且以d2为分歧参数考察了系统的Hopf分歧，得到了非齐次周期解存在的条件.

Gierer-Meinhardt模型；分歧；双重特征值；Hopf分歧

0 引言

反应扩散系统的模式形成于包括化学和生物系统的各种机理中，是非线性物理学中最有趣的现象之一.因此，近几十年来很多工作致力于模式的研究，比如文献［1-3］研究了化学模型，文献［4-7］研究了生物模型.

本文讨论Gierer-Meinhardt模型

其中：Ω是RN中带有光滑边界∂Ω的有界区域；ν是外单位法向量；u和v分别表示活化剂和抑制剂的浓度；b和m分别表示u和v的衰减率；d1和d2是扩散系数；参数d1，d2，b和m都是正常数；常数p，q， r，s满足关系p＞1，q＞0，r＞0，s≥0，且；初值u0（x）和v0（x）是连续函数.

近年来，许多学者从数值模拟和理论分析上对系统（1）进行了广泛的研究［8－12］.文献［8］给出了系统正解的先验估计和唯一性.文献［9］研究了Gierer-Meinhardt模型内部峰值的动力学行为.文献［12］在二维情况下讨论了系统（1）的K-峰值不对称模式的存在性和稳定性.

本文主要研究一维情况Ω＝（0，2π）下系统（1）的平衡态系统.为了方便起见，我们取p＝2，q＝1，r＝2，s＝0，则系统（1）的平衡态系统为

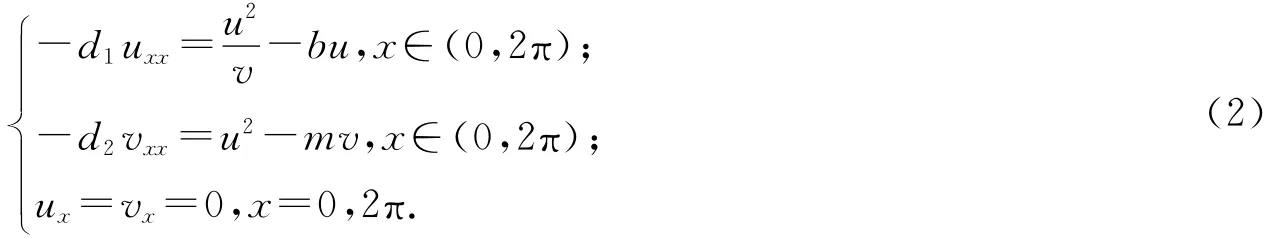
目前，关于系统（2）的稳态分歧和Hopf分歧的理论分析很少见，尤其是二重特征值的分歧.因此本文集中讨论系统（2）的稳态分歧和Hopf分歧.

1 正常数解的稳定性

显然，系统（2）有唯一正常数解U＊＝（u＊，v＊），这里.在此给出系统（2）的常数解U＊的稳定性.众所周知，特征值问题

系统（2）在U＊处的线性化算子为

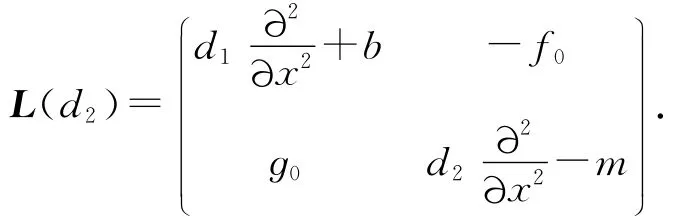
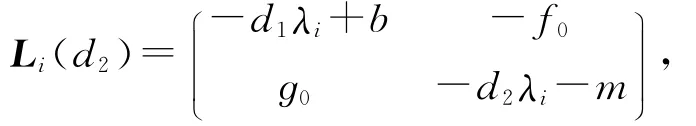
它的特征方程为

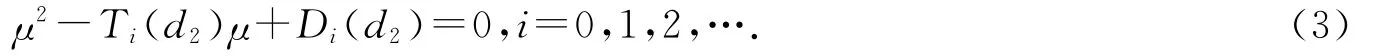
其中

定理1 下面的稳定性结果成立：

（ⅰ）如果b＜min｛d1λ1，m｝，则U＊渐近稳定.

（ⅱ）如果m＜b＜d1λ1，则U＊不稳定.

（ⅳ）记d2，i，¯d2和I0如（ⅲ）所示.若m＜b＜m＋d1λ1，则对于0＜d2＜¯d2，U＊不稳定.

证明 （ⅰ）因为b＜min｛d1λ1，m｝，所以b－m＜0.于是，对所有的d2＞0和i≥0，可知Ti（d2）＜0.由于b＜d1λ1，因此b＜d1λi，i≥1.于是当d2＞0和i≥1时，Di（d2）＝d2λi（d1λi－b）＋md1λi＋bm＞0.当d2＞0和i＝0时，D0（d2）＝bm＞0.因此，L（d2）的所有特征值有负实部.故对所有的d2＞0，U＊是渐近稳定的.

（ⅱ）由于b＜d1λ1，因此对所有的d2＞0，i≥1，Ti（d2）＜0.显然在假设条件下，T0（d2）＝b－m＞0.另一方面，由（ⅰ）可知对所有的d2＞0，i≥0，Di（d2）＞0.所以，L（d2）有正实部的特征值.因此，对所有的d2＞0，U＊是不稳定的.

（ⅲ）首先，由b＜m可知对任意的i≥0，d2＞0，都有Ti（d2）＝－（d1＋d2）λi＋b－m＜0.当d2＞0和i＝0时，D0（d2）＝bm＞0.当1≤i≤I0时，D′i（d2，i）＝λi（d1λi－b）＜0.显然，对任意的1≤i≤I0，Di（d2，i）＝0.所以当1≤i≤I0，d2＜¯d2时，Di（d2）＝d1d2λ2i＋［md1－bd2］λi＋bm＞d1d2，iλ2i＋［md1－bd2，i］λi＋bm＝0.另一方面，当i＞I0时，结合I0的定义可得Di（d2）＝d2λi（d1λi－b）＋md1λi＋bm＞0.于是，对任意的i≥0，d2＜¯d2，都有Di（d2）＞0.这就说明Li（d2）的所有特征值有负实部.因此，对所有的d2＞0，U＊是渐近稳定的.

（ⅳ）类似于（ⅲ）的证明方法可得，对任意的i≥0，0＜d2＜¯d2，都有Di（d2）＞0.当d2＞0和i＝0时，由b＞m可知T0（d2）＝b－m＞0.另一方面，对任意的d2＜¯d2，当1≤i≤I0时，由于T′i（d2，i）＝－λi＜0，且Ti（0）＝－d1λi＋b－m＜－d1λ1＋b－m＜0.所以Ti（d2）＜Ti（0）＜0.当i＞I0时，b－d1λi＜0.因此，Ti（d2）＝－（d2λi＋m）＋b－d1λi＜0.这就说明L（d2）有正实部的特征值.因此，对所有的d2＞0，U＊是不稳定的.

2 分歧解的存在性

我们利用分歧理论来研究系统（2）正常数解U＊处的分歧解.固定b，m，d1，将d2＞0作为分歧参数，利用局部分歧理论、空间分解和隐函数定理给出非常数正解的存在性.

令Y＝Lδ（0，2π）×Lδ（0，2π），内积为（U1，U2）Y＝（u1，u2）L2（0，2π）＋（v1，v2）L2（0，2π），其中U1＝（u1，v1），U2＝（u2，v2）∈Y.记X＝｛（u，v）∈W2，δ（0，2π）×W2，δ（0，2π）：ux＝vx＝0，x＝0，2π｝.定义映射F：R＋×X→Y为

易知系统（2）的解等价于F的零点.显然，F（d2，U＊）＝0.下面假定b＞d1，于是存在正整数Id2使得b－d1λi＞0，1≤i≤Id2.令（3）式中的μ＝0，可得

定理2 假定b＞d1.取

（ⅰ）若存在正整数j，1≤j≤Id2，使得任意的整数i≠j，1≤i≤Id2都有dS2，i≠dS2，j成立，则（dS2，j，U＊）是F＝0的一个分歧点.当0＜｜s｜≪1时，系统（2）存在非常数解曲线Γ2（s）＝（d2（s），u（s），v（s）），其中d2（s），u（s），v（s）是连续函数，且满足d2（0）＝dS2，j，u（s）＝u＊＋sφj＋o（s），v（s）＝v＊＋sbjφj＋o（s），bj＝另外，在分歧点，U＊）的小邻域内，F的零点集由两条曲线｛（d2，U＊）｜d2＞0｝和Γ2（s）构成.

（ⅱ）若存在正整数i≠j，1≤i，j≤Id2，使得＝＝.令

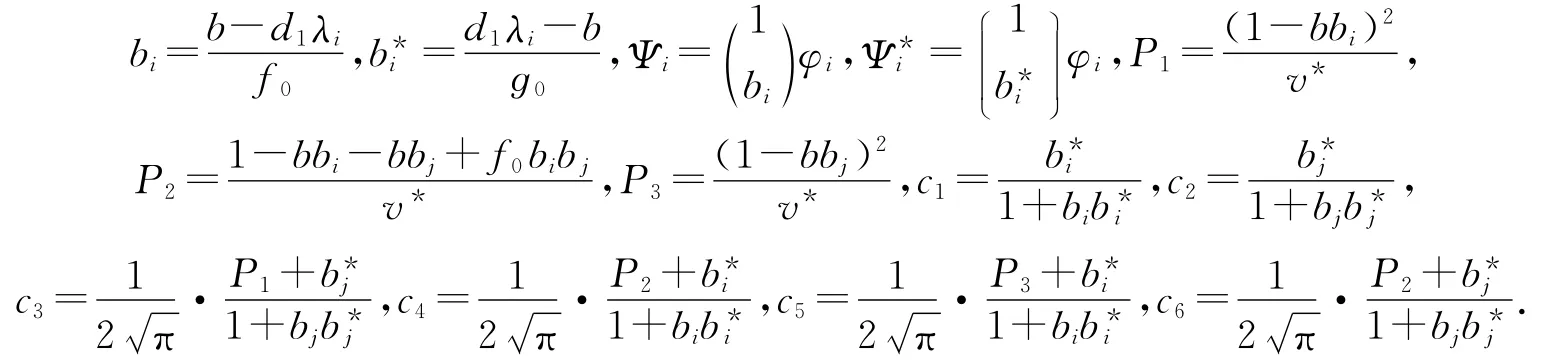
如果1＋bib＊i≠0，1＋bjb＊j≠0，P1＋b＊j≠0，P2＋b＊i≠0，P3＋b＊i≠0，P2＋b＊j≠0，且j＝2i（或i＝2j），则（~d2，U＊）是F＝0的一个分歧点，且当0＜｜α－α0｜≪1时，存在系统（2）的非常数解曲线（d2（α），U＊＋s（α）（cosαΨi＋sinαΨj＋W（α））），其中d2（α），s（α），W（α）是连续函数，且满足d2（α0）＝~d2，s（α0）＝W（α0）＝0，这里α0是满足如下条件的任意常数：

或

证明 （ⅰ）用类似于文献［12］定理3的方法可证得.

（ⅱ）如果存在正整数i≠j，使得dS2，i＝dS2，j＝~d2，则此时

所以，dim kerL（~d2）＝codimR（L（~d2））＝2.显然，局部分歧定理失效.现在，我们求助于空间分解和隐函数定理来讨论二重分歧解的存在性.首先，做变换＾u＝u－u＊，＾v＝v－v＊.定义新的映射¯F：R＋×X→Y为

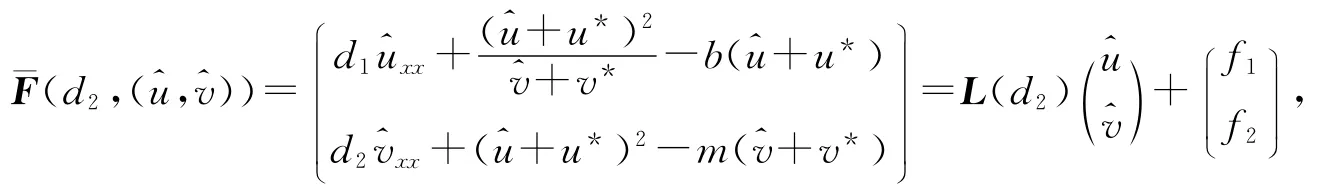
接着，我们分解空间X为X＝X1⊕X2，其中

寻找¯F＝0的形式为

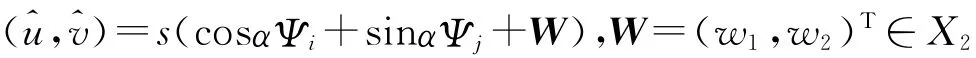
的解，这里s，α∈R是参数.为了后面的需要，定义算子P：Y→X1为

根据投影的定义可验证P是投影.于是，我们分解空间Y为Y＝Y1⊕Y2，其中Y1＝R（P）＝X1，Y2＝kerP＝R（L（~d2））.

我们应用隐函数定理证明非常数对（＾u，＾v）的存在性.固定α0∈R，定义非线性映射

为

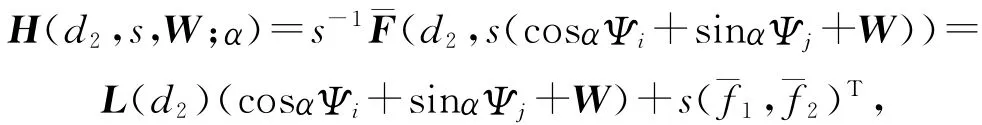
其中

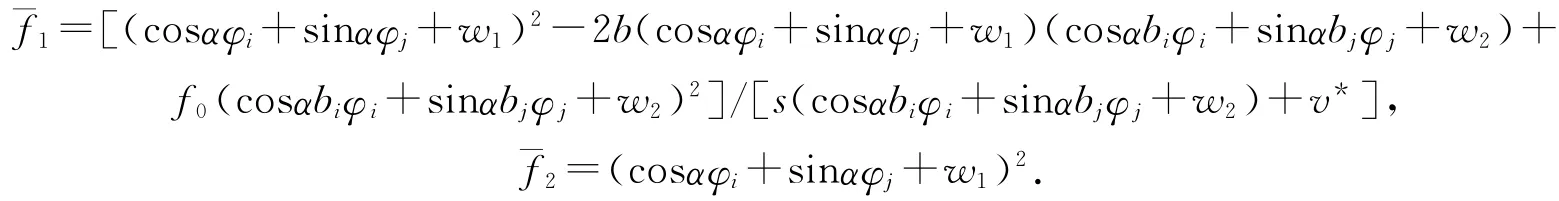
显然，H（~d2，0，0；α0）＝0.而且，H（d2，s，W；α）关于（d2，s，W）在（~d2，0，0；α0）处的Fréchet导数

为

为了应用隐函数定理，我们需要证明线性映射H（d2，s，W）（~d2，0，0；α0）：R×R×X2→Y是双射.为此，重记H（d2，s，W）（~d2，0，0；α0）（d2，s，W）＝y1＋y2，这里y1∈Y1，y2∈Y2.简单计算可知

再分解

其中

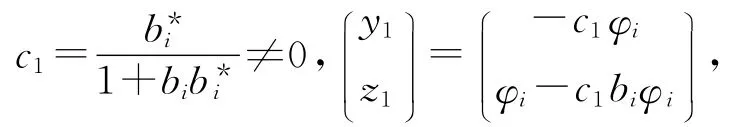
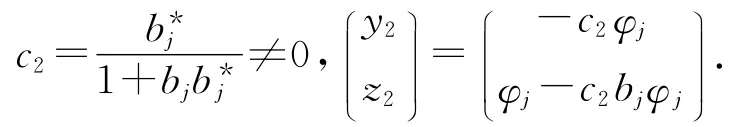
接下来，分两种情况讨论：

分解

其中：

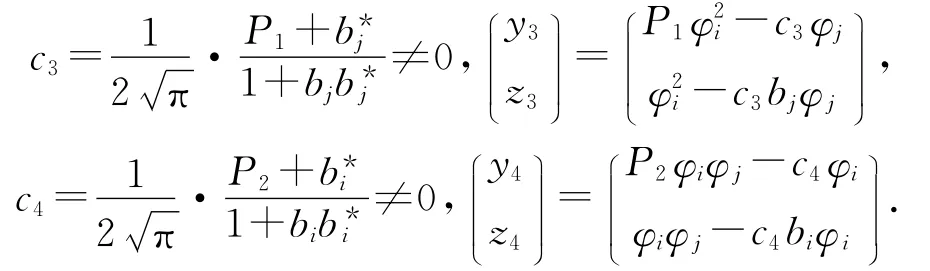
易知L（~d2）：X2→Y2是双射.假设：

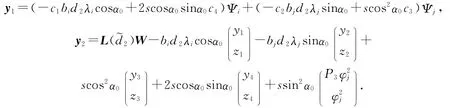
首先，我们证明L＝H（d2，s，W）（~d2，0，0；α0）是单射.令L（d2，s，W）＝0，则y1＝0，y2＝0.由于cosα0≠0，（c1c3biλi＋2c2c4bjλj）sin2α0≠c1c3biλi.所以由y1＝0易知d2＝0，s＝0.将d2＝0，s＝0，带入y2＝0中可得W＝0.于是，L是单射.

其次，证明L是满射.需要证明对任意的（y，z）∈Y，存在（d2，s，W）∈R×R×X2，使得

由Y的分解可知存在β，γ∈R和（y0，z0）∈Y2，使得

将上式带入（7）式可得

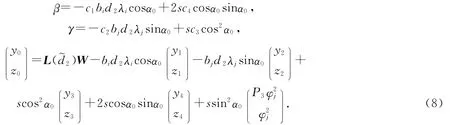
由（8）式的前两个式子可得

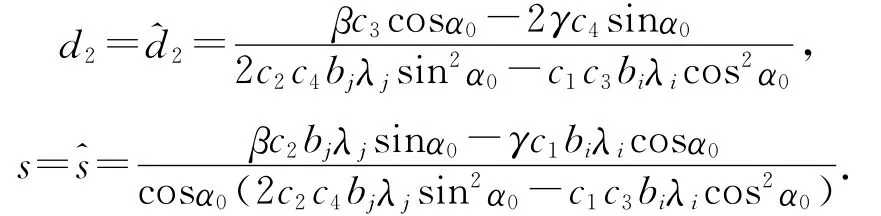
由于当j＝2i时α0满足（4）式，所以上式有意义.再将＾d2，＾s带入到（8）式的第三个式子中得

这里

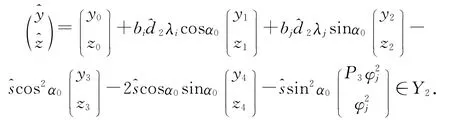
于是，（d2，s，W）＝（＾d2，＾s，L－1（~d2）（＾y，＾z）T）.因此，L是满射，即L是双射.由隐函数定理可知H（d2，s，W；α）＝0，在α0的小邻域内有非常数解（d2（α），s（α），W（α）），满足d2（α0）＝~d2，s（α0）＝W（α0）＝0，这里α0满足（4）式.而且，d2（α），s（α），W（α）是连续可微函数且W∈X2.因此，（d2（α），U＊＋s（α）（cosαΨi＋sinαΨj＋W（α）））是F＝0的非常数正解.

（B）i＝2j.类似于（A）的证明过程可得，如果α0满足（5）式，则应用隐函数定理可知这种情况的结论也成立.

最后，用类似于文献［13］定理4的方法将定理2（ⅰ）中的局部分歧延拓为全局分歧.

3 Hopf分歧

我们讨论系统（2）的常数解U＊的Hopf分歧周期解的存在性.令α（d2）＋iβ（d2）是L（d2）的复特征值，即方程（3）的复根，则.由文献［14］可知如果存在整数i0≥0和dH2＞0使得

证明 显然，T1（dH2，1）＝0，对于所有的i≥2都有Ti（）≠0.而且，对所有的d2＞0，在假设条件下T0（d2）＝b－m＞0.由于对于所有的d2＞0，D0（d2）＝bm＞0.因此，我们只需要验证D1（）＞0和对所有的i≥2，Di（dH2，1）≠0即可.将带入到D1）中，经过简单计算可知D1（）＞0等价于

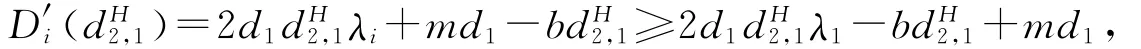
I＝2d11－b＋md1.将带入到I＝0中，整理可得

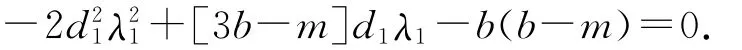
最后证明α′（dH2，1）≠0.对于i＝1，系统（3）在d2＝dH2，1附近的共轭复根为.因此，系统（2）在点（dH2，1，U＊）处产生Hopf分歧，即在常数解U＊附近系统（2）产生非齐次周期解.

［1］ BROWN K J，DAVIDSON F A.Global bifurcation in the Brusselator system［J］.Nonlinear Analysis：Theory，Methods and Applications，1995，24（12）：1713-1725.

［2］ WANG M X.Non-constant positive steady states of the Sel'kov model［J］.J Differential Equations，2003，190（2）：600-620.

［3］ KOLOKONIKOV T，MICHAEL J，WEI J.The existence and stability of spike equilibria in the one-dimensional Gray-Scott model on a finite domain［J］.Applied Mathematics Letters，2005，18（8）：951-956.

［4］ LOU Y，NI W M.Diffusion，self-diffusion and cross-diffusion［J］.J Differential Equations，1996，131：79-131.

［5］ DU Y H，LOU Y.Qualitative behavior of positive solutions of a predator-prey model：effects of saturation［J］.Proc Roy Soc Edinburgh A，2001，131；321-349.

［6］ PENG R，WANG M X.Positive steady-states of the Holling-Tanner predator-prey model with diffusion［J］.Proc Roy Soc Edinburgh A，2005，135：149-164.

［7］ 高芳，王文爽，王静.带有食饵避难的Leslie-Gower捕食者-食饵扩散系统的稳定性及最优税收［J］.东北师大学报：自然科学版，2014，46（2）：1-8.

［8］ TAKAGI I.A priori estimates for stationary solutions of an activator-inhibitor model due to gierer and meinhardt［J］.Tôhoku Math Journ，1982，34：113-132.

［9］ CHEN X F，KOWALCZYK M.Dynamics of an interior spike in the Gierer-Meinhardt system［J］.Siam J Math Anal，2001，33（1）：172-193.

［10］ WEI J，WINTER M.Spikes for the Gierer-Meinhardt system in two dimensions：the strong coupling case［J］.J Differential Equations，2002，178（2）：478-518.

［11］ CHOI Y S，MCKENNA P J.A singular Gierer-Meinhardt system of elliptic equations：the classical case［J］.Nonlinear Anal，2003，55（5）：521-541.

［12］ WEI J，WINTER M.Existence and stability analysis of asymmetric patterns for the Gierer-Meinhardt system［J］.J Math Pures Appl，2004，83：433-476.

［13］ JANG J，NI W M，TANG M X.Global bifurcation and structure of turing patterns in the 1-D Lengyel-Epstein model［J］.Journal of Dynamics and Differential Equation，2004，16：297-309.

［14］ YI F Q，WEI J，SHI J P.Bifurcation and spatiotemporal patterns in a homogeous diffusive predator-prey system［J］.J Differential Equations，2009，246：1944-1977.

Stability analysis and spatially bifurcation for a Gierer-Meinhardt model

LI Hai-xia
（Institute of Mathematics and Information Sciences，Baoji University of Arts and Sciences，Baoji 721013，China）

The steady-states bifurcations and Hopf bifurcation for a Gierer-Meinhardt model with homogeneous Neumann boundary conditions are considered.The stability of the positive constant solution is discussed.Furthermore，the bifurcations from simple and double eigenvalues are investigated by means of the combination of the simple bifurcation theory，space decomposition and implicit function theorem.Finally，by regarding d2as a bifurcation parameter，we study the Hopf bifurcation and obtain the conditions of the existence of inhomogeneous periodic solution.

Gierer-Meinhardt model；bifurcation；double eigenvalue；Hopf bifurcation

O 175.26 ［学科代码］ 110·4730

A

（责任编辑：陶 理）

1000-1832（2015）03-0026-07

10.16163／j.cnki.22-1123／n.2015.03.006

2014-09-23

中央高校基本科研业务费专项资金资助项目（GK2013 02025）；陕西省教育厅专项科研计划项目（14JK1035）；宝鸡文理学院重点科研项目（ZK15039）.

李海侠（1977—），女，博士，讲师，主要从事偏微分方程计算及其可视化研究.