分子动力学模拟计算超临界CO2的溶解度参数

罗 辉，王 睿，范维玉，李兆敏，马 涛，南国枝

(1. 中国石油大学 重质油国家重点实验室， 山东 青岛 266580； 2. 中国石油大学 石油工程学院， 山东 青岛 266580；3.拜耳材料科技(中国)有限公司， 上海 200120)

分子动力学模拟计算超临界CO2的溶解度参数

罗 辉1,2，王 睿1，范维玉1，李兆敏2，马 涛3，南国枝1

(1. 中国石油大学 重质油国家重点实验室， 山东 青岛 266580； 2. 中国石油大学 石油工程学院， 山东 青岛 266580；3.拜耳材料科技(中国)有限公司， 上海 200120)

采用分子动力学模拟方法，计算了超临界CO2和超临界CO2-乙醇体系的溶解度参数，并分析了体系内粒子间距离的径向分布函数。结果表明，超临界CO2的溶解度参数随温度的升高而减小，随压力的增大而增大，且随密度的增大而线性增大；添加乙醇可明显提高超临界CO2的溶解度参数，且随着乙醇浓度的增加，在相同条件下的溶解度参数也增大。乙醇分子可与CO2分子形成分子间氢键而提高CO2的极性，从而提高体系的溶解度参数；超临界CO2-乙醇体系中，分子间，特别是乙醇分子间存在聚集现象。当体系压力较低时，增大压力，可大幅度减弱乙醇分子间的聚集程度，使体系的溶解度参数迅速增大；但继续增大压力到一定程度时，乙醇分子间的聚集程度达到定值，即乙醇已均匀分散在CO2中，溶解度参数随压力的变化趋于平缓。

超临界CO2；溶解度参数；分子动力学模拟；乙醇

超临界流体作为安全、高效的绿色溶剂，得到了广泛的关注和应用[1-2]。CO2具有较为温和的临界条件，同时还具有无毒、无污染、不燃烧、容易回收和循环利用的优点。目前，超临界CO2已成为应用最为广泛的超临界流体，并成功地应用在萃取分离、化学反应以及石油开采等领域[3-6]。溶解性能是超临界CO2的重要性质之一，研究其在各种操作条件下的溶解能力，可为它的工业化应用提供必要的理论指导，同时对萃取等操作过程的机理研究也有着重要的意义。

可以采用溶解度参数对溶剂的溶解能力进行定量评价。溶解度参数为液体内聚能密度的平方根[7]，可采用量热法等实验方法[8]测定，也可采用基团贡献法等理论估算方法[9]得到。常见的有机溶剂已经有比较完整的溶解度参数数据，但对于超临界流体来说，它的溶解度参数会随温度和压力的变化而改变，即不同各操作条件下的溶解度参数值不同，需进行大量的实验来确定。因此，有必要开发一种可以简单并准确计算超临界CO2溶解度参数的方法[10]。

分子动力学(MD)模拟方法可以从分子水平上有效地理解化学物理过程，能在给定的温度、压力条件下准确地预测体系的各种热力学性质[11-13]。Vimon等[14]采用MD模拟和量子化学半经验分子轨道AM1方法，夏庆等[15]采用MD模拟方法，计算了常见化合物的溶解度参数，结果表明，在常温、常压条件下，计算值与实验值吻合良好。但当溶剂达到超临界状态时，MD模拟方法是否还可适用，需进一步的研究与验证。因此，笔者尝试采用MD模拟方法对超临界CO2在不同温度、压力下的溶解度参数进行模拟计算，并考察乙醇作为夹带剂对超临界CO2溶解度参数的影响。

1 溶解度参数的计算方法

利用Material studio 6.0软件包中的Amorphous Cell模块构建包含300个分子的周期性立方盒子，如图1所示。纯CO2体系时，该立方盒子含300个CO2分子；含5%的乙醇时，该立方盒子含285个CO2分子和15个乙醇分子，以此类推。构建好模型后即可采用Forcite模块进行MD模拟计算。使用的力场为出自量子力学从头计算的Compass力场[16]。MD模拟采用NPT系综，采用Anderson方法对体系的温度和压力进行控制。模拟时间为500 ps，步长为1.0 fs，每1000步输出1帧。采用Group方法计算范德华力和库仑相互作用力，截断半径为1.55 nm。

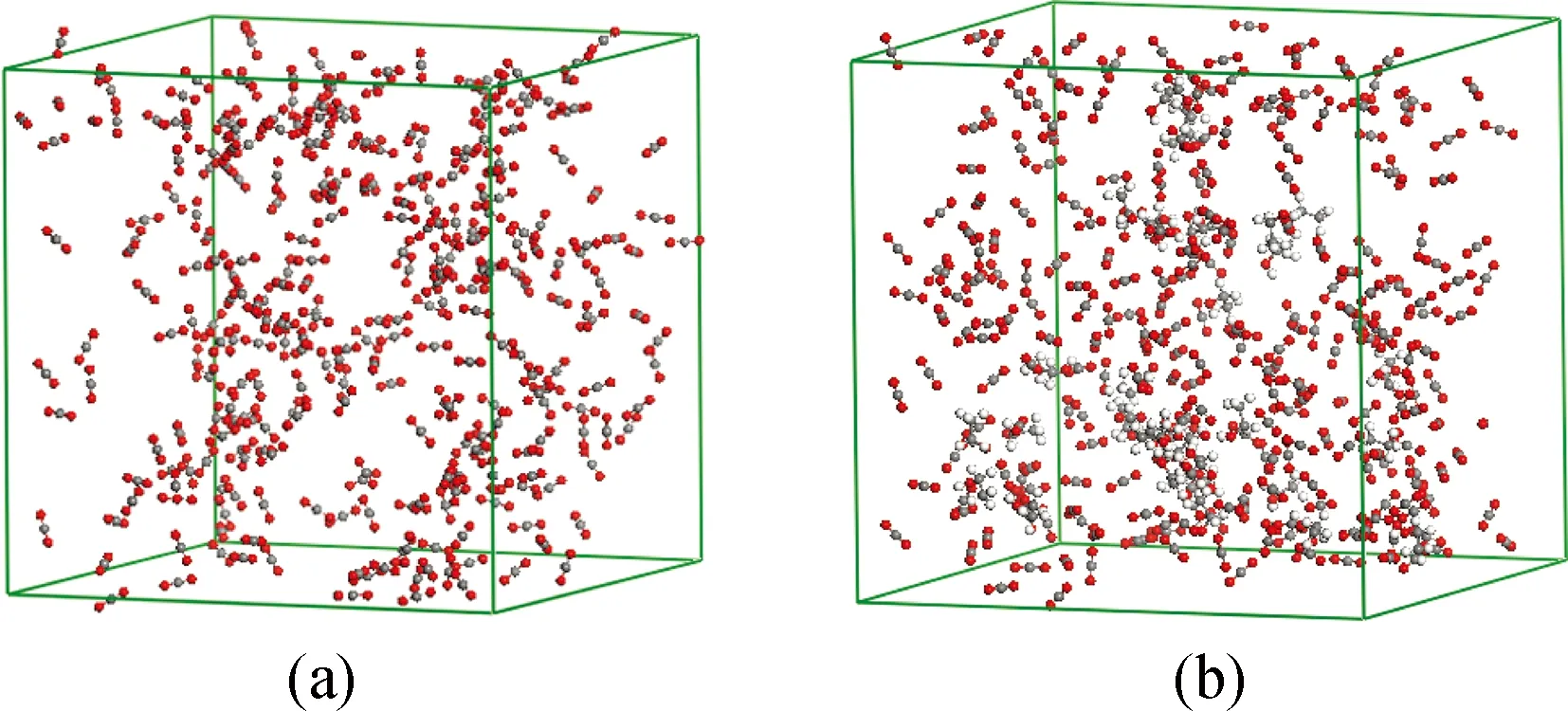
图1 超临界CO2体系的初始模型

当体系的温度变化和密度变化趋于平稳时，则认为体系达到平衡。通过分析平衡体系的内聚能密度，便可计算溶解度参数。为了验证计算的准确性，模拟计算了超临界CO2在不同温度、压力条件下的密度，并与实验值[17]进行对比，结果列于表1。由表1可以看出，模拟得到的密度与实验值吻合，相对误差均在6%以内，说明MD模拟计算方法及结果可靠。

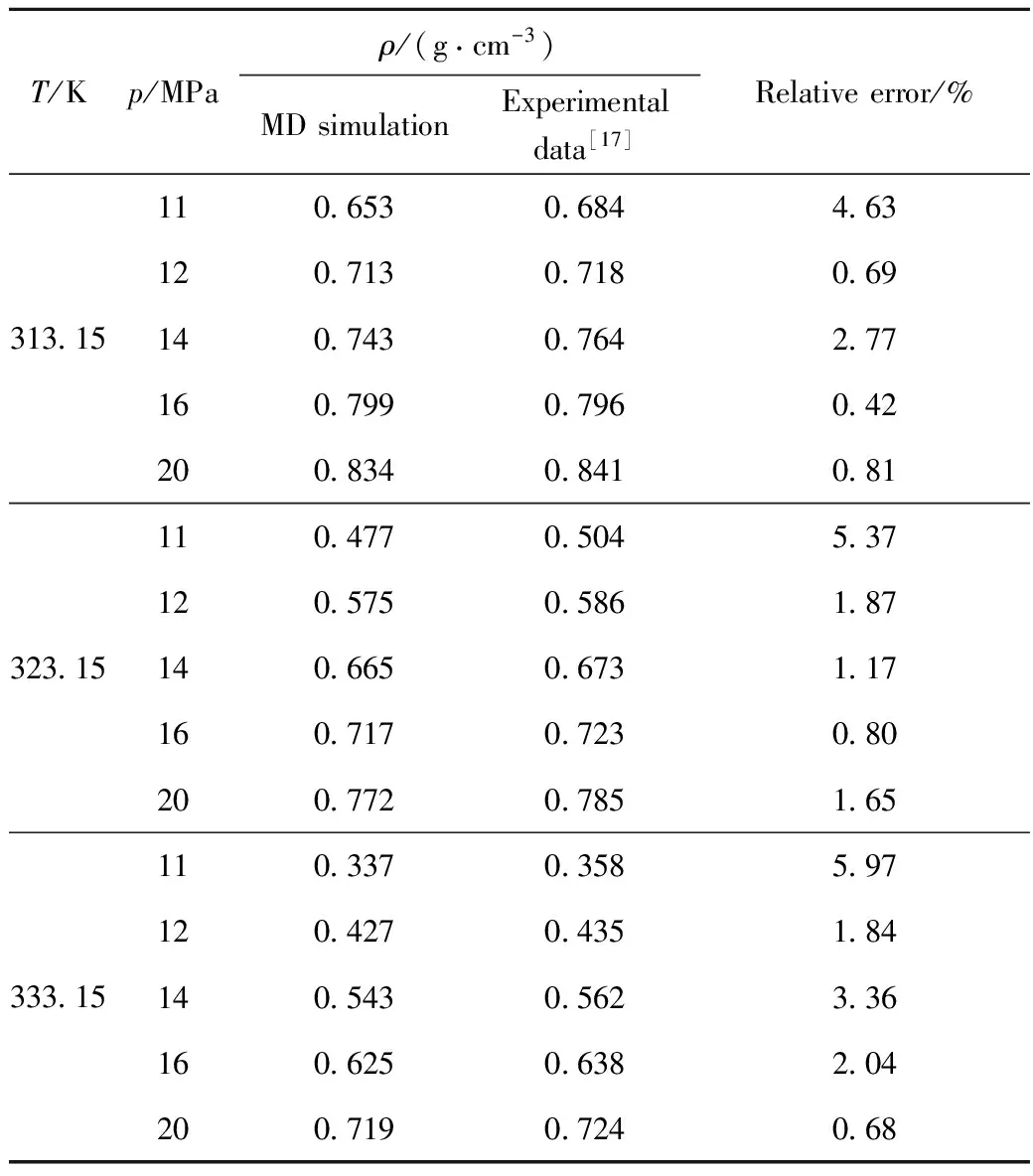
表1 超临界CO2密度的MD模拟值与实验值[17]

2 结果与讨论

2.1 温度、压力对超临界CO2溶解度参数的影响

超临界CO2的溶解能力与温度和压力密切相关，即可通过改变温度和压力来调节其溶解度参数，选择性地溶解某些物质从而达到萃取分离的目的。图2为不同温度、压力条件下超临界CO2的溶解度参数。由图2可知，超临界CO2的溶解度参数随温度的升高而减小，随压力的增大而增大。温度的升高会加剧分子的热运动，减弱分子间的相互作用力而使溶解能力变弱；增大体系的压力会使分子间的距离减小而增强分子间的相互作用力，导致溶解度参数增大。

通常认为，操作温度、压力对超临界流体溶解能力的调控主要是通过改变体系的密度来实现。图3为密度对超临界CO2溶解度参数的影响。由图3可见，超临界CO2的溶解度参数随密度的增大而线性增大。

图2 不同温度、压力条件下超临界CO2的溶解度参数(δ)

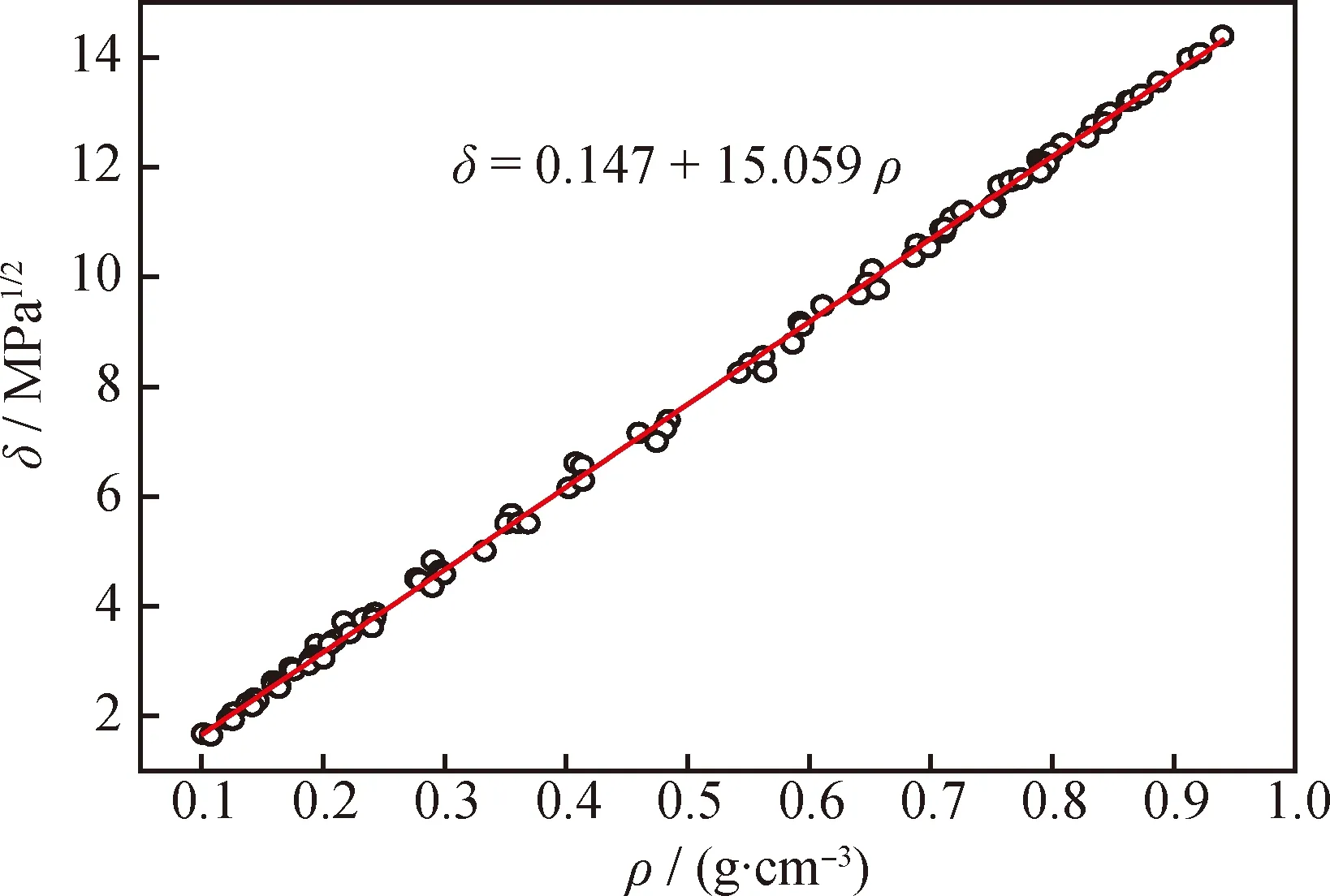
图3 密度(ρ)对超临界CO2溶解度参数(δ)的影响

2.2 夹带剂乙醇对超临界CO2溶解度参数的影响

从图2可以看出，当压力较高时，再进一步增大压力，溶解度参数的增加幅度趋于平缓，此时单纯靠提高压力或降低温度并不能显著提高CO2的溶解能力。但对于一些极性溶质来说，如脂肪酸、稠油等，它们的溶解度参数较大，需要较大幅度地提高超临界CO2的溶解度参数才能将它们溶解。向超临界CO2中添加少量的极性夹带剂，如甲醇、乙醇、丙酮等，可以明显改善CO2对极性溶质的溶解性能[18]。因此，考察了体系温度为320K时乙醇摩尔分数对超临界CO2溶解度参数的影响，结果如图4所示。

图4 320 K时乙醇摩尔分数对超临界CO2溶解度参数(δ)的影响

由图4可知，添加乙醇可明显地提高超临界CO2的溶解度参数，且随着乙醇摩尔分数的增加，在相同条件下的溶解度参数也增大。另外，在各乙醇摩尔分数下，体系溶解度参数随压力的变化均存在一个明显的拐点。在拐点处，体系的溶解度参数会大幅度增加，当压力高于拐点值时，继续增加体系压力，溶解度参数开始平缓增加。而且，随着体系中乙醇摩尔分数的提高，拐点压力越低。乙醇摩尔分数为5%、10%和20%时的拐点压力分别为9、8和5 MPa。

同样，考察了320 K时超临界CO2-乙醇体系的溶解度参数与密度的关系，结果如图5所示。由图5可知，当乙醇摩尔分数一定时，体系的溶解度参数随密度的增大呈线性增大，且乙醇摩尔分数越大，直线的斜率和截距越大。

2.3 超临界CO2-乙醇体系中粒子间距离径向分布函数

径向分布函数g(r)的定义如式(1)所示。

(1)

图5 320 K时超临界CO2-乙醇体系的密度(ρ)与溶解度参数(δ)的关系

式(1)中，ρ为体系的密度，N为体系中粒子的数目，dN为半径r、厚度dr的球壳内粒子数目。径向分布函数可以解释为体系在r处的区域密度与体系平均密度的比值，可反映出体系中分子聚集的特性；在径向分布函数曲线中，最高峰的位置说明此处的区域密度最大，即出现其他粒子的概率最大[19]。

为了解释夹带剂乙醇对超临界CO2溶解度参数的影响规律，计算了温度为320 K、乙醇摩尔分数为10%时，超临界CO2-乙醇体系中CO2分子-CO2分子、乙醇分子-乙醇分子、CO2分子-乙醇分子、乙醇羟基的H原子-乙醇羟基的O原子、以及乙醇羟基的H原子-CO2的O原子间的径向分布函数g(r)，分析压力对分子间聚集状态的影响，结果如图6所示。

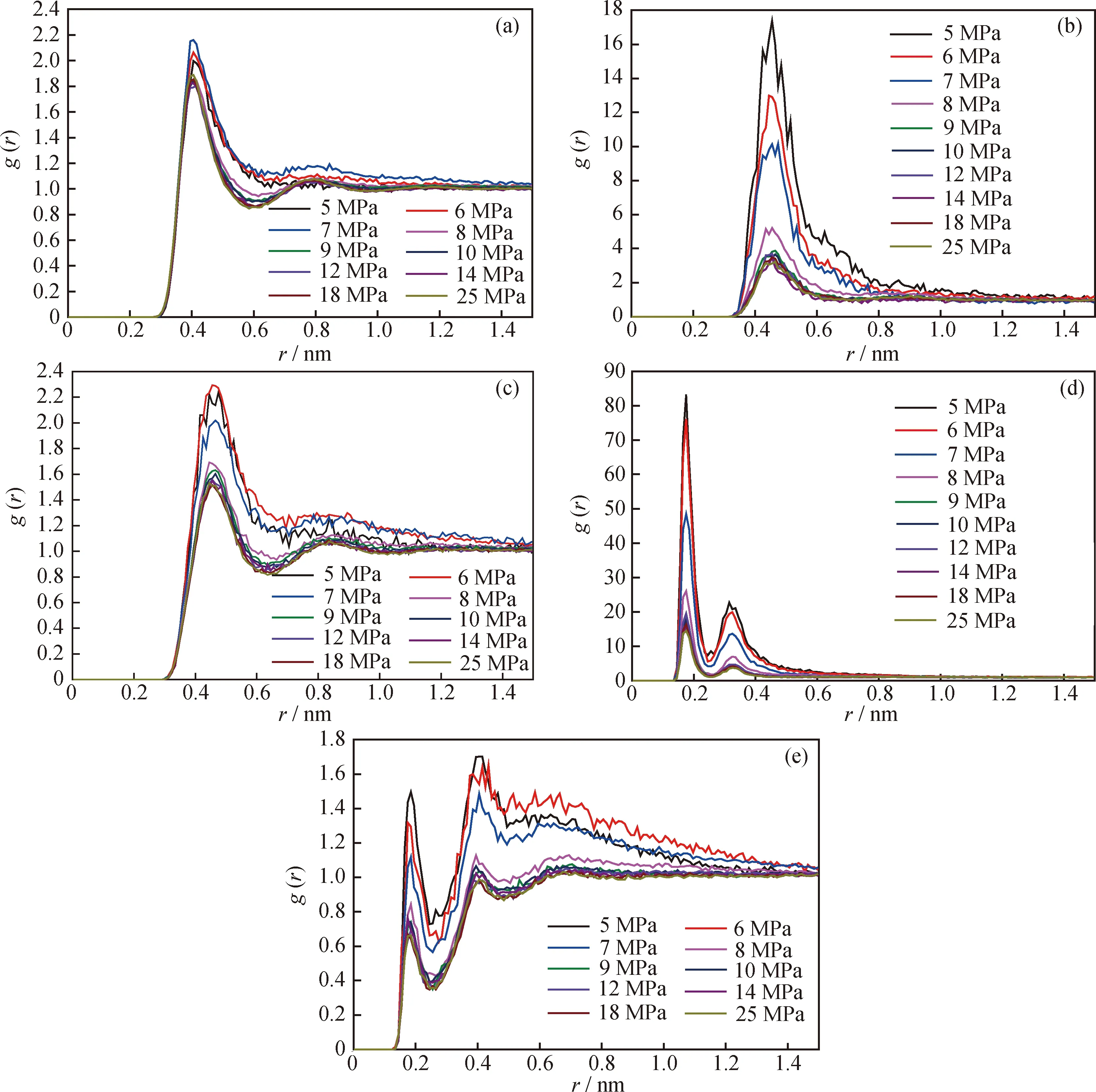
图6 超临界CO2-乙醇体系中粒子间距离径向分布函数(g(r))

从图6(a)、(b)、(c)可知，不同的压力条件下，CO2分子-CO2分子、乙醇分子-乙醇分子、CO2分子-乙醇分子的g(r)均在r为0.405、0.455、0.455nm处分别出现了1个明显的峰。说明在夹带乙醇的超临界CO2体系中，CO2及乙醇分子间均发生了聚集现象[20]。且随着压力的增大，g(r)的峰值降低，说明分子间的聚集现象随着压力的增大而减弱。特别是乙醇分子-乙醇分子间的g(r)，在压力较低时的峰值较大，如在5、6、7和8 MPa时的峰值分别为17.4、12.9、10.1和5.2，而当压力大于8 MPa时，峰值基本保持不变。说明在低压条件下，由于超临界CO2的可压缩性高，分子间的自由空间非常大，导致乙醇在分子间引力的作用下形成了非常紧密的聚集结构；而随着压力的增大，CO2的可压缩性减小，分子的自由空间减小，使乙醇分子间的聚集程度减弱。

从图6(d)和6(e)来看，乙醇羟基的H原子-乙醇羟基的O原子间及乙醇羟基的H原子-CO2的O原子间的g(r)分别在r为0.175、0.185 nm附近出现了尖峰，说明乙醇分子间、以及乙醇分子与CO2分子间均形成了明显的氢键。乙醇分子与CO2分子间的氢键可提高CO2分子的极性，从而提高超临界CO2体系的溶解度参数。另外，氢键原子间的g(r)的峰值大小随压力的变化规律与分子间的g(r)一致，因此，分子间的氢键是体系中形成聚集体的主要原因之一。

图7 320 K时不同压力下乙醇分子-乙醇分子间径向分布函数的峰值(g(r)max)

由图7可知，在不同乙醇浓度的体系中，随着压力的增加，g(r)max均表现出类似的变化规律；当压力较低时，随着压力的增大，g(r)max急剧下降；但当压力高于某一值时，g(r)max趋于平稳，与图4溶解度参数随压力变化曲线中所出现的拐点对应。因此，增大体系的压力，减弱乙醇分子间的聚集程度，即提高乙醇分子在CO2中的分散程度，可使体系的溶解度参数迅速增大；但当压力增大到一定程度时，乙醇分子间的聚集程度达到定值，即乙醇已均匀分散在CO2中，此时，再继续增大压力，不会再显著提高体系的溶解度参数。

3 结 论

(1)分子动力学模拟计算结果表明，超临界CO2的溶解度参数随温度的升高而减小，随压力的增大而增大，随密度的增大而线性增大。

(2)添加乙醇可明显地提高超临界CO2的溶解度参数，且乙醇浓度越高，在相同条件下的溶解度参数也越大。

(3)超临界CO2-乙醇体系中，分子间，特别是乙醇分子间存在聚集现象。当体系压力较低时，增大压力可大幅度减弱乙醇分子间的聚集程度，使体系的溶解度参数迅速增大；但压力增大到一定程度时，乙醇分子间的聚集程度达到定值，再继续提高压力，溶解度参数不再明显增大。

[1] 韩布兴. 超临界流体科学与技术[M]. 北京：中国石化出版社，2005.

[2] SKERGET M, KNEZ Z, KNEZ-HRNCIC M. Solubility of solids in sub- and supercritical fluids：A review [J]. Journal of Chemical Engineering Data, 2011, 56(4)：694-719.

[3] DAVARNEJAD R, KASSIM K M, ZAINAL A, et al. Supercritical fluid extraction ofβ-carotene from crude palm oil using CO2[J]. Journal of Food Engineering, 2008, 89(4)：472-478.

[4] PERAKIS C, LOULI V, VOUTSAS E, et al. Supercritical CO2extraction of dittany oil：Experiments and modeling [J]. The Journal of Supercritical Fluids, 2010, 55 (2)：573-578.

[5] BAIKER A. Supercritical fluids in heterogeneous catalysis [J]. Chemical Reviews, 1999, 99(2)：453-473.

[6] DONG Z, LI Y, LIN M, et al. A study of the mechanism of enhancing oil recovery using supercritical carbon dioxide microemulsions [J]. Petroleum Science, 2013, 10(1)：91-96.

[7] HILDEBRAND J H, SCOTT R L. The Solubility of Non-electrolytes [M]. New York：Dover, 1964.

[8] MAJER V, SVOBODA V, PICK J. Heats of Vaporization of Fluids [M]. Amsterdam：Elsevier, 1989:53-60.

[9] 黄向红. 重结晶的溶剂选择与溶解度参数之间的关系[J]. 化学通报，1999, 1(1)：35-38. (HUANG Xianghong. Relationship between the choice of recrystallization solvents and their solubility parameters [J]. Chemistry, 1999, 1(1)：35-38.)

[10] SAMBASLVA R A. Solubility parameters of supercritical fluids [J]. Industrial Engineering Chemistry Process Design and Development, 1984, 23 (2)：344-348.

[11] HEADEN T F, BOEK E S. Molecular dynamics simulations of asphaltene aggregation in supercritical carbon dioxide with and without limonene [J]. Energy Fuels, 2011, 25(2)：503-508.

[12] LI X, ROSS D A, TRUSLER J P M, et al. Molecular dynamics simulations of CO2and brine interfacial tension at high temperatures and pressures [J]. Journal Physical Chemistry B, 2013, 117(18)：5647-5652.

[13] 罗辉，范维玉， 李阳，等. 生物柴油组分在铁表面吸附的分子动力学模拟[J]. 石油学报(石油加工)，2013, 29(3)：416-421. (LUO Hui, FAN Weiyun, LI Yang, et al. Molecular dynamics simulation on the adsorption behaviors of biodiesel components on iron surface [J]. Acta Petrolei Sinica (Petroleum Processing Section), 2013, 29(3)：416-421.)

[14] VIMON T, NIMIT W, WIBUL W. Prediction of solubility parameters using partial least square regression [J]. International Journal of Pharmaceutics, 2006, 325(1-2)：8-14.

[15] 夏庆，殷开梁. 分子动力学模拟计算有机溶剂的溶解度参数[J]. 江苏工业学院学报，2004, 16(1)：40-42. (XIA Qing, YIN Kailiang. Calculation of solubility parameters of organic solvents by molecular dynamics simulation [J]. Journal of Jiangsu Polytechnic University, 2004, 16(1)：40-42.)

[16] SUM H. Compass： An ab initio force-field optimized for condensed-phase applications-overview with details on alkane and benzene compounds[J]. Journal Physical Chemistry B, 1998, 102(38)：7338-7364.

[17] KHIMECHE K, ALESSI P, KIKIC I, et al. Solubility of diamines in supercritical carbon dioxide experimental determination and correlation [J]. The Journal of Supercritical Fluids, 2007, 41(1)：10-19.

[18] DOBBS J M, WONG J M. Modification of supercritical fluid phase behavior using polar cosolvents [J]. Industrial Engineering Chemistry Research, 1987, 26(1)：56-65.

[19] 陈正隆，徐为人， 汤立达. 分子模拟的理论与实践[M]. 化学工业出版社，2007.

[20] TUCKER S C, MADDOX M W. The effect of solvent density inhomogeneities on solute dynamics in supercritical fluids：a theoretical perspective [J]. Journal Physical Chemistry B, 1998, 102(14)：2437-2453.

Calculation of Solubility Parameters of Supercritical CO2by Molecular Dynamics Simulation

LUO Hui1, 2, WANG Rui1, FAN Weiyu1, LI Zhaomin2, MA Tao3, NAN Guozhi1

(1.StateKeyLaboratoryofHeavyOilProcessing,ChinaUniversityofPetroleum,Qingdao266580,China;2.SchoolofPetroleumEngineering,ChinaUniversityofPetroleum,Qingdao266580,China;3.BayerMaterialScience(China)Co.Ltd.,Shanghai200120,China)

The solubility parameters of supercritical CO2and supercritical CO2-ethanol system were calculated by molecular dynamics simulation. The radial distribution function of the systems was analyzed. The results indicated that the solubility parameter of supercritical CO2decreased with the increase of temperature, increased with the increase of pressure, and increased linearly with the density of the system. Addition of ethanol could significantly improve the solubility parameter of supercritical CO2, and the solubility parameter increased with the increase of ethanol concentration under the same condition. It was found that the intermolecular hydrogen bonds were formed between ethanol and CO2, thereby the polarity and the solubility parameter of supercritical CO2increased. There was intermolecular aggregation in supercritical CO2-ethanol system, especially, in ethanol molecules. When the pressure was lower, aggregation of the ethanol molecules would be significantly weakened with the increase of pressure. However, when the pressure increased to a certain extent, aggregation of the ethanol molecules tended to be smooth, meaning that the ethanol molecules were evenly dispersed in CO2, and the solubility parameter gently increased with the increase of pressure.

supercritical CO2; solubility parameter; molecular dynamics simulation; ethanol

2013-12-24

中国博士后科学基金项目( 2014M551987)资助 第一作者： 罗辉，男，讲师，博士，从事石油化学方面的研究；Tel：0532-86983032; E-mail：luohuidcnh@163.com

范维玉，男，教授，博士，从事石油化学与胶体界面化学方面的研究；Tel：0532-86981863; E-mail：fanwyu@upc.edu.cn

1001-8719(2015)01-0078-06

TE626.24

A

10.3969/j.issn.1001-8719.2015.01.013