时域平面近场散射测量研究

吴 洋薛正辉任 武李伟明徐晓文

时域平面近场散射测量研究

吴 洋1，2薛正辉2任 武2李伟明2徐晓文2

（1.电磁散射重点实验室，北京100854；2.北京理工大学信息与电子学院，北京100081）

时域平面近场散射测量是一种在近场区域进行散射测量的技术，可以有效地进行宽带的散射测量，具有超宽带测试、可以获得时域散射场、空间利用率高等特点.针对时域平面近场散射测量技术体系，在时域近场测量的理论基础上，提出了系统组建方案，论证了系统的可行性，开展了针对典型目标的验证测试，并对测量结果进行了初步的误差分析.证明了时域平面近场散射测量的有效性.

时域；近场；雷达散射截面；多角度

引 言

随着对散射问题研究的深入，针对复杂散射目标的宽带散射特性和雷达散射截面积（Radar Cross Section，RCS）的有效测量是检验理论分析结果和掌握实际数据的必要手段，也具有强烈的工程需求.目前散射测量方式主要分为传统远场测量与室内等效远场测量（紧缩场测量）两种［1－3］.这两种测量技术在发展成熟、应用广泛的同时，也都有一定的局限性.

近场测量技术［4］中的频域近场散射测量技术是近二十年基于频域近场辐射测量技术发展而来的.它在待测目标散射场的近场区域内作采样测试，消除了远场中的距离效应；一次测试过程就可以得到一个较大立体角域的三维远场散射像；可利用频域技术有效地减少测量时间［5－9］；测量过程在室内进行，安全保密，排除了天气的因素的影响；利用现代数据分析和计算手段进行近远场外推，可以同时获得近场和远场的散射数据.但是它还存在着一些局限性：一次测试只能测试较少频点；由于采样面截断造成的测试误差难于消除和抑制等.

时域近场测量技术是20世纪90年代末期出现的新兴技术［10－11］.本文阐述的时域平面近场散射测量是基于时域平面近场辐射测量技术［12－15］发展而来的.它具有以下特点：属于超宽带测试，可以得到目标宽带散射像；可以采用各种有效的时域信号处理技术，减少误差；可以获得时域散射远场，掌握散射远场的建立过程；与室内等效远场测量不同，测量目标大小只受到采样架运动范围的影响，不受到接收天线尺寸的影响.随着对于宽带、超宽带散射测量需求的增加，我们相信在可预见的未来，时域近场散射测量是具有广阔的工程应用前景的.

文中提出了一种完整的时域平面近场散射测量系统组成方案，系统介绍了时域平面近场散射测量的理论基础，提出了系统硬件和软件子系统的构建方案；通过组建时域平面近场散射测量实验系统并开展初步的验证实验，对测试结果进行误差分析，证明了所提出设计方案的有效性.

1 时域平面近场散射测量系统组成

时域平面近场测量系统组成包括硬件子系统、软件子系统以及采样方案三个部分.系统在一次完整的测量过程中可以得到待测目标在测量频段内近场采样面范围内时域散射场数据和测量频段内全部频域近场散射场数据、远场一定立体角域内时域散射场和测量频段内全部频域远场散射场.

硬件子系统包括微波暗室、采样架、测量信号发射接收设备、控制装置、接收探头和发射天线等.其中微波暗室与采样架设备与其他近场测量系统的不同之处在于，测量用信号源为满足时域测量需要有产生脉冲信号的能力，所以一般选用任意信号发生器、突波发生器等设备作为信号源.同时接收设备也需要有相应的时域信号接收能力，如采样示波器.

在时域平面近场散射系统中，将发射天线架设在远场区，以发射天线的辐射远场模拟平面波照射待测目标，利用测试探头在目标散射近场区域内进行信号采集，考虑到多角度下的散射测量对易实现性和易搬运性的要求，以标准增益喇叭天线作为发射天线.实际测量时测量系统的搭载情况如图1所示.

软件子系统包括近场数据采集控制和数据处理、结果显示三个部分.采集控制软件主要是控制采样架移动，实现近场数据采集；数据处理软件是将近场采样得到数据进行处理，以得到远场的散射信息；结果显示软件是将数据处理软件计算的结果可视化.

采样方案如图2所示，通过改变采样面与入射波的相对位置，可以实现多角度下的散射测量.

图1 时域平面近场散射测量系统硬件子系统

图2 采样方式示意图

在一个完整的数据采集过程中，需要经过四次扫描采样.在图2中所示坐标系中，不失一般性地以极化方向与x轴平行的入射波为例.在放置待测目标的情况下，探头极化以平行于x轴方向进行扫描采样，获得主极化方向下的近场总场Exx（t）；将探头旋转，使其极化方向垂直于x轴再次进行扫描采样，获得交叉极化方向下的近场总场Exy（t）；将待测目标移出测量区域，重复上述两次扫描采样分别获得主极化方向下的入射场Eixx（t）和交叉极化方向下的入射场Eixy（t）.再经由公式

可以获得近场主极化方向的散射场Esxx（t）和交叉极化方向的散射场Esxy（t）.至此整个测量的近场数据采集部分结束.近场区获得的Esxx（t）和Esxy（t）两个极化方向上的近场散射场不是传统意义上所定义的垂直－垂直极化（VV极化）下的远场散射场EsVV和垂直——水平极化（VH极化）下的远场散射场EsVH.Esxx（t），Esxy（t）时近场区两个切向方向的散射场，远场散射场EsVV和EsVH都是由这两个近场散射共同决定的.

将获得散射场数据以及入射场数据带入到数据处理部分进行近远场外推从而获得远场散射场信息.远场散射场信息中的远场散射电场包括Esθ，Esφ两个方向的散射电场.一般远场和紧缩场散射测量中VV极化和VH极化下的远场散射场是Esθ，Esφ的线性组合.

入射场信息，由于属于辐射近场测量，背景噪声相对入射场来说很小，影响不大，可以直接由空载时主极化方向采样获得的Eixx（t）直接确定.

2 时域平面近场散射测量的理论基础

在时域平面近场测量框架下，RCS可以经由两种途径得到.其一，时频域平面近场散射测量.将时域近场散射数据进行傅里叶变换得到频域近场散射数据，再经过频域平面波谱展开理论得到频域远场散射数据，进而得到RCS.其二，纯时域平面近场散射测量.直接由时域平面波谱展开理论得到时域远场散射数据，再经过傅里叶变换得到频域远场散射数据，进而得到RCS.在此，首先系统介绍时频域平面近场散射测量的基本理论，再以频域结果为基础推导出纯时域近场散射测量理论公式.

根据文献［10－11，15］可以得到变换对

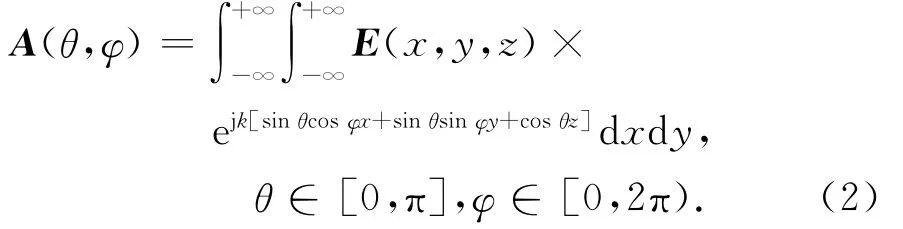
通过公式（1）建立了谱函数A（θ，φ）与近场电场分量E（x，y，z）之间的关系.

其中

公式（3）建立了远场电场分量E（r0）与谱函数A（θ，φ）之间的关系.

根据驻相法，可以得到方程（3）的近似表达式为

根据雷达散射截面积的定义式

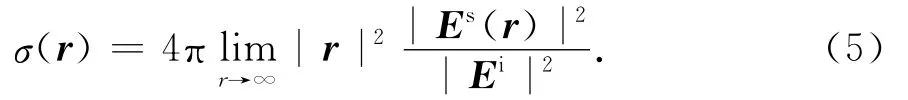
式中：Es（r）是远场散射电场；Ei为入射电场.

将公式（4）中计算得到的远场散射电场分量Es（r）带入公式（5）得到最终的RCS计算公式为

在时频域公式的基础上，介绍纯时域平面近场散射测量的公式推导.

根据傅里叶变换，时域远场电场可以表示为

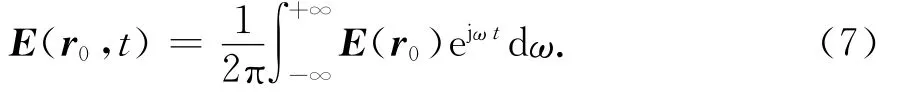
式中r0为场点坐标.将式（4）带入式（7），可以变换为

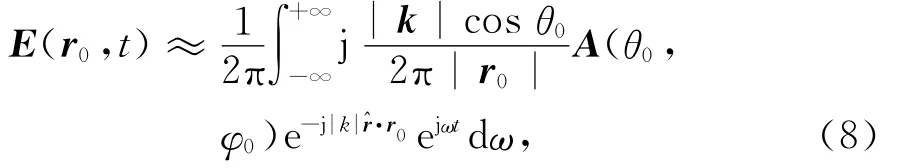
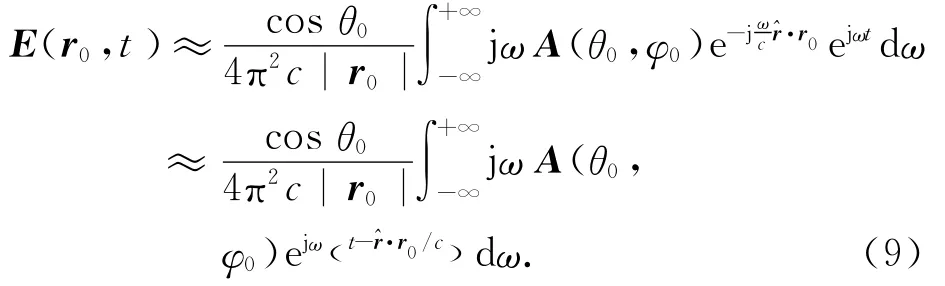
式中c为光速.根据式（9），与频域波谱函数对照，可定义时域波谱为

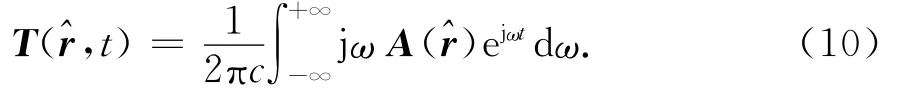
从而电场远场表达式为

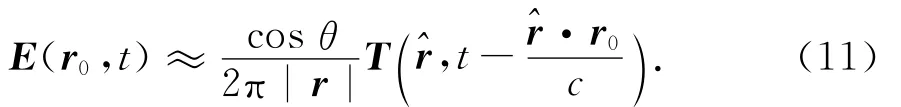
这是电场远场E（r0，t）与时域波谱T（＾r，t）之间的关系式.其中θ的取值范围由于是平面近场测试的缘故，只取［0，π／2）.

将式（2）带入式（10）可以得到时域波谱T（＾r，t）和频域近场电场E（r0）之间的关系式为

式中E（r0）是在近场直角坐标系下表示的.

根据傅里叶变换的基本性质，最终时域波谱与时域近场电场之间的关系式可以表示为

将由公式（14）得到的远场散射电场Es（r0，t）经过傅里叶变换到频域后带入方程（5）既可得到RCS.

3 测量结果与误差分析

以天线时域近场测试系统［15］为基础，构建了时域平面近场散射测量实验系统，实际测量中，由于突波发生器的信号不够稳定，将通过信号耦合的方式获得入射场信息，用来对探头接收到的信号做时基修正［15］.在实测结果中，金属球的实测结果都向半径（πa2）进行了归一.

为了验证时域平面近场散射实验系统在不同角度下的正确性，又对0.1m半径和0.2m半径的金属球在9～11GHz的前向散射和135°进行了两组测量.并对直接测量与对比测量进行结果对比.对比测量法主要是应用于无法得到准确入射场下计算远场RCS的一种测量手段，可以在不计算入射场值的情况下，得到待测目标的远场RCS.

在前向RCS（θ＝180°）测试中，测量参数为：待测目标为0.2m半径金属球；发射天线与接收天线分别为8～12GHz标准增益喇叭和开口波导探头；采样面尺寸2m×2m；采样点间隔0.012 5m；0.1 m半径金属球作为定标体.

比较图3中的时域信号，可以发现，相较于突波发生器发出的入射场信号，由探头接收到的总场信号存在一定的色散，这符合开口波导探头接收的特点.

图4中前向RCS测量的误差在全测量频段内控制在2dB以内.由于实际测量中0.2m半径金属球摆放位置有所偏差，造成采样面中心未完全对准球心，所以0.2m球的实测误差要大于0.1m球的误差.

初步分析误差产生的原因：

1）测试用信号源功率低，导致采样数据幅值过低.一般都在－65dB至－35dB之间，在幅值较小处受杂波影响比较大，虽然利用对消技术减小了部分影响，但是还是不能消除这种误差.

图3 参考信道的时域入射场信号与有目标时的采样面中心点的采样信号

图4 9～11GHz金属球前向RCS对比

2）由于场地条件限制发射天线与待测目标距离过近，入射场不满足准平面波要求.由于发射天线方向图的影响，导致RCS计算偏小.通过采样面中心点附近多点求平均确定入射场值的方法，减小了这种误差.最后结果与理论结果的误差控制在了3 dB以内.

3）采样面截断造成的误差.

4）缺少探头修正.由于散射测试需要绝对修正而不是天线测试的相对修正，对于其中的常数的确定还有待摸索.

在图5中，为前向RCS水平方向结果.在测量中，采样面边缘与待测目标中心所形成的张角约为±55°.如图5所示，直接测量法的可信角域约为± 35°～±40°.可信角域估算约为采样面边缘与待测目标中心所形成的张角－15°.实际测量结果与理论解之间除个别点外，误差在3dB以内.

图5中对比测量法得到的0.2m金属球的前向RCS水平方向结果与直接测量法基本一致，两种测量方法互为对照.并且对比测量法的可信角域范围较直接测量法结果要大一些，基本达到了±40°～± 45°.图5中，RCS振荡区域，由于采样点间隔问题，造成空间分辨率不足，实际测量结果与理论解在振荡区域并不十分吻合.

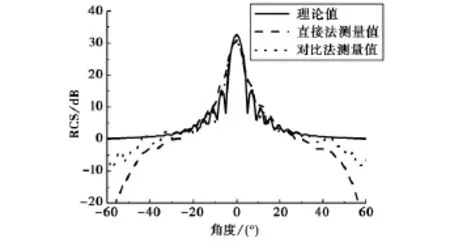
图5 10GHz时0.2m半径金属球前向区域水平切面RCS对比

对于测量结果的评判采用了以dB为单位的均方差进行评判.以此为标准计算得到：直接测量法0.2m球前向RCS测量结果中±40°内的81个角度计算点dB差的均方差为3.063 5；直接测量法0.1 m球前向RCS测量结果中±40°内的81个角度计算点dB差的均方差为1.987（中间结果未给出图示）.在相同的测试条件下，两个球的均方差误差相差1dB，可以说明摆放精度对于金属球前向散射测量准确度有很大影响.对比测量法0.2m球修正后前向RCS测量结果中±40°内的81个角度计算点的均方差为2.278.在±30°范围内这三个均方差分别为3.028、1.891、2.494.对比法测量结果和直接法测量结果误差相当.

图6所示，θ＝135°，φ＝90°方向RCS测量中，采用对比测量法进行测量.实际测量中，采样面边长设置为1.5m，其他设置与前向RCS测量中的设置相同.

图6 0.2m半径金属球θ＝135°，φ＝90°方向水平切面RCS对比

由于采样面的减小，相应的可信角域也有所降低.实际测量结果的均方差为：±40°内的81个角度计算点dB差的均方差为1.847；±30°内的61个角度计算点dB差的均方差为1.575.

4 结 论

时域平面近场散射测量可以有效地进行宽带散射测量，相较其他测试手段，具有超宽带测试，可以获得时域散射场、空间利用率高等特点.本文对时域平面近场测量系统从系统设计到测量过程进行了详细的阐述.系统介绍了其理论基础，设计了一个较为实用的测量系统并进行实际测量验证.对于测量结果中的误差给出了初步分析.在分析误差产生原因的基础上，给出了相应的可行的修正手段.通过实验仿真与实际测量的结果，证明了平面近场散射测量的有效性.

作为一种直接测量手段，时域平面近场散射测量系统亦可以通过对比测量减少环境设备等的固有误差，但是测量时间成本和计算成本要有相应的增加.系统中部分误差修正还有待研究，在测试过程中的绝对探头修正系数以及可信角域的量化估算还需要进一步探究，这是后续开展这方面研究的主要方向.

［1］ 庄钊文，袁乃昌.雷达散射截面测量——紧凑场理论与技术［M］.长沙：国防科技大学出版社，2000.

［2］ 陈伯孝，胡铁军，朱 伟，等.VHF频段隐身目标缩比模型的雷达散射截面测量［J］.电波科学学报，2011，26（3）：480－485.

CHEN Baixiao，HU Tiejun，ZHU Wei，et al.RCS measurement for scale model of stealth targets in VHF band［J］.Chinese Journal of Radio Science，2011，26（3）：480－485.（in Chinese）

［3］ 金 旺，吴 健，吴振森，等.930MHz雷达测空间碎片散射截面［J］.电波科学学报，2012，27（6）：1076－1080.

JIN Wang，WU Jian，WU Zhensen，et al.Space debris cross section observations with 930MHz radar［J］.Chinese Journal of Radio Science 2012，27（6）：1076－1080.

［4］ KERNS D M.Plane－wave scattering－matrix theory of antennas and antenna－antenna interactions［J］.NASA STI／Recon Technical Report N，1981，82：15358.

［5］ DINALLO M A.Extension of Plane－Wave Scattering－Matrix Theory of Antenna－Antenna Interactions to Three Antennas：A Near－Field Radar Cross Section Concept［R］.Bdm Corp Albuquerque Nm，1985.

［6］ COWN B J，RYAN Jr C.Near－field scattering meas－urements for determining complex target RCS［J］.IEEE Transactions on Antennas and Propagation，1989，37（5）：576－585.

［7］ LAHAIE I J，LEBARON E I，BURNS J W.Far field radar cross－section（RCS）predictions from planar near field measurements［C］／／IEEE Antennas and Propagation Society International Symposium.Chicago：IEEE，1992：1542－1545.

［8］ BUCCI O M.Effective evaluation of monostatic RCS from nearfield data［C］／／Proc AMTA，1999.

［9］ BUCCI O M，MIGLIORE D.Effective estimation of 2－D monostatic radar cross sections from near－field measurements［J］.IEEE Transactions on Antennas and Propagation，2006，54（2）：750－752.

［10］ HANSEN T B，YAGHJIAN A D.Planar near－field scanning in the time domain.1.Formulation［J］.IEEE Transactions on Antennas and Propagation，1994，42（9）：1280－1291.

［11］ HANSEN T B，YAGHJIAN A D.Planar near－field scanning in the time domain.2.Sampling theorems and computation schemes［J］.IEEE Transactions on Antennas and Propagation，1994，42（9）：1292－1300.

［12］ 陈国华.天线平面时域近场测试误差仿真分析研究［D］.北京：北京理工大学，2004：45－51.

CHEN Guohua.Error Analysis by Simulation in Time Domain Planar Near Field Antenna Measurement［D］.Beijing：Beijing Institute of Technology，2004：45－51（in Chinese）

［13］ 刘 超，薛正辉，高本庆，等.时域近场测量采样平面选择分析［J］.电波科学学报，2000，15（4）：512－516.

LIU Chao，XUE Zhenghui，GAO Benqing，et al.The analysis and selection of sampling plane in time－domain near－field measurement［J］.Chinese Journal of Radio Science，2000，15（4）：512－516.（in Chinese）

［14］ 刘 超，薛正辉，高本庆，等.时域近场测试中的采样面截断误差分析与修正［J］.微波学报，2000，17（2）：81－84.

LIU Chao，XUE Zhenghui，GAO Benqing，et al.Samplingplane truncation errors analysis and correction in timedomain nearfield measurement［J］.Journal of Microwaves，2000，17（2）：81－84.（in Chinese）

［15］ WANG N，XUE Z H，YANG S M，et al.Antenna time domain planar near field measurement system［J］.International Journal on Wireless ＆Optical Communications，2006，3（2）：127－133.

Time domain planar near field scattering measurement

WU Yang1，2XUE Zhenghui2REN Wu2LI Weiming2XU Xiaowen2
（1.Science and Technology on Electromagnetic Scattering Laboratory，Beijing100854，China；2.School of Information and Electronics Beijing Institute of Technology，Beijing100081，China）

Time domain planar near field scattering measurement is a direct and effective method.It has some advantages，such as wide frequency band，holonomic time domain scattering data，high space utilization and so on.In this paper，the technical architecture of time domain planar near field scattering measurement is illustrated.Based on the principle of time domain planar near field scattering measurement，the construction scheme of this measurement system is designed，and the feasibility is proved.The effectiveness of this system is proved by analyzing the actual measurement data and corresponding errors.

time domain；near field；RCS；multi－angle

O441.5

A

1005－0388（2015）02－0351－06

吴 洋（1984－），男，北京人，电磁散射重点实验室工程师，北京理工大学信息与电子学院，电磁场与微波技术专业博士生，主要从事时域近场辐射与散射测量方面研究.

薛正辉（1970－），男，上海人，北京理工大学信息与电子学院副教授.1992年毕业于北京理工大学电子工程系，1995年在同校电磁场与微波技术专业获得工学硕士学位并留校任教，2002年获得北京理工大学电磁场与微波技术专业博士学位.主要从事电磁场与微波技术方面的教学和计算电磁学、电磁兼容及天线测量技术、微波毫米波技术方面的有关研究.

任 武（1976－），男，山西人，副教授，中国电子学会高级会员，“三遥”分会委员，2003年在北京理工大学电磁场与微波技术专业获得博士学位，在北京理工大学信息与电子学院任教，主要从事计算电磁学、仿真技术研究.

吴 洋，薛正辉，任 武，等.时域平面近场散射测量研究［J］.电波科学学报，2015，30（2）：351－356.

10.13443／j.cjors.2014051505

WU Yang，XUE Zhenghui，REN Wu，et al.Time domain planar near field scattering measurement［J］.Chinese Journal of Radio Science，2015，30（2）：351－356.（in Chinese）.doi：10.13443／j.cjors.2014051505

2014－05－15

联系人：薛正辉E－mail：zhxue＠bit.edu.cn