基于LMI的一类混沌系统同步控制及仿真

高子林 熊 江 罗卫敏 鄢 沛

（重庆三峡学院计算机科学与工程学院，重庆万州 404100）

基于LMI的一类混沌系统同步控制及仿真

高子林 熊 江 罗卫敏 鄢 沛

（重庆三峡学院计算机科学与工程学院，重庆万州 404100）

针对一类混沌系统，进行了基于线性矩阵不等式(LMI)的同步控制器的设计，使混沌系统的各个状态均能较快地达到同步状态．该方法只需求解矩阵K，运算量非常小，满足了工业中实时性的要求，具有一定的有效性和可行性．

混沌系统；同步控制器；LMI

1 引 言

混沌系统控制分为混沌系统同步控制和混沌系统稳定控制．1990年，Pecora和Carrol[1]提出了驱动响应同步控制方法并用电路实现，同年，Ott，Grebogy和Yorke提出参数微扰动方法OGY方法[2]，完成了混沌系统的稳定控制，此后，混沌系统理论和应用研究渗入到各个领域，如物理、生物系统和保密通信系统等[3-5]．在过去的二十年里，混沌系统控制得到了迅猛发展，研究人员提出各种控制方法，如模糊自适应方法，滑模变结构控制方法，反馈方法及神经网络方法等[6-9]．这些控制算法为了解决混沌系统中存在的未知非线性，算法比较复杂，导致运算量特别大，从而产生较大的时滞，这有悖于实际应用中实时性的要求．

由于混沌系统在实际应用时通常其动态方程是给定的[10-11]，为了减小运算量，实现在保密通信等实际应用中实时性的要求，本文提出基于LMI的一类混沌系统同步控制设计，并利用Lyapunov稳定性理论证明了该方法的正确性．该方法设计简单，运算量小，在混沌系统同步控制的应用中具有实际的工程意义．

2 模型描述及基本假设

考虑如下标准的混沌动态驱动系统[12]

其中，未知参数α∈[0，1]．当α∈[0，0.8）时，系统（1）为Lorenz混沌系统；当α=0.8时，系统（1）为Lü混沌系统；当α∈（0.8，1]时，系统(1)为Chen混沌系统．

为了控制设计的方便，可以将系统（1）改写为如下形式：

系统（1）的响应系统如下[12]:

同样地，可以将系统（3）改写成如下形式：

其中，控制输入u=（u2u3）T∈Rm；g是一个未知的常数增益系数，且g≠0．

设状态误差为e=y-x，由（2）和（4）式可得如下误差动态方程

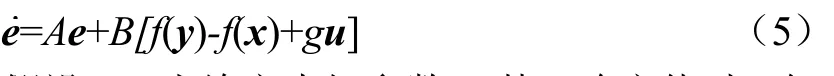
假设1．当给定未知参数α某一确定值时，矩阵对（A，B）是完全可控的，即对于一个给定的正定矩阵Q，存在一个m×n的矩阵K使如下Lyapunov方程有且只有一个正定对称矩阵解P

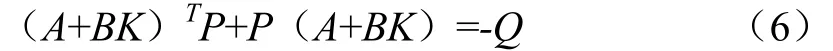
注1．在Lyapunov方程（6）中，矩阵K可以通过求解线性矩阵不等式XAT+AX+BY+YTBT＜0获得，其中X＞0，且X=P-1，Y=KX．

3 同步控制器设计及分析

控制目标：设计控制器（7）和矩阵K，使状态向量eT有界并且使驱动系统（1）和响应系统（2）渐近同步，即

针对上述控制目标，对响应系统（4）提出如下控制方案：其中K是根据（6）式求得的．

定理1．考虑驱动系统（1）和响应系统（2），如果假设1成立，那么通过控制器（7）的作用，可以达到控制目标的要求．

证明：考虑正定函数V（t）=eTPe．如果假设1成立，那么正定函数V（t）关于时间t的导数如下：

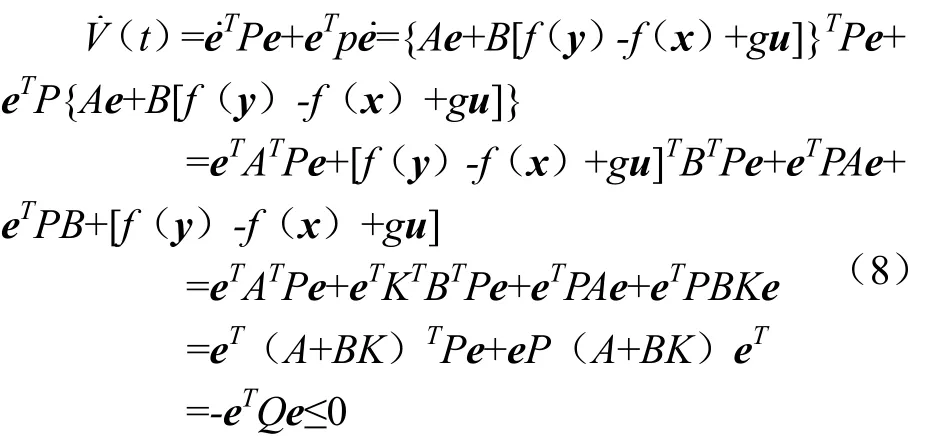
不等式（8）表明误差动态方程（5）的状态向量是有界的；根据Barbalat[13]引理可知从而完成了定理1的证明．

4 仿真算例

假设2：在系统仿真的过程中，给定的正定矩

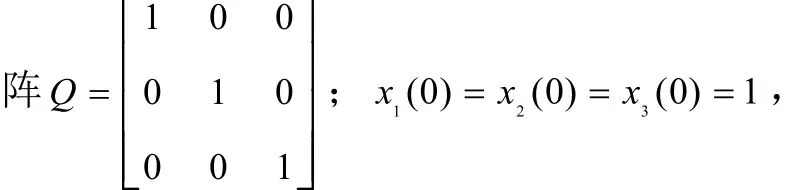
y1（0）=y2（0）=y3（0）=10．

（1）当α=1时，系统（1）为Chen混沌系统，

由（2）式知根

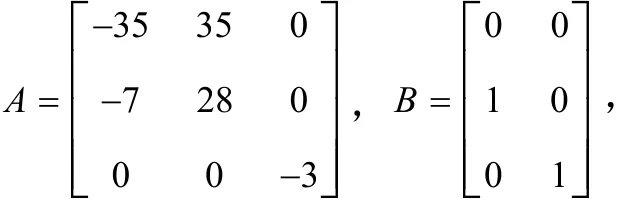
应用于响应系统（3）中，仿真结果如图1所示：

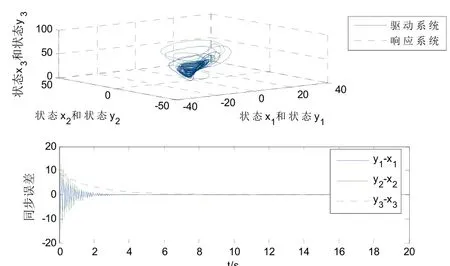
图1 三维同步相位图及同步误差图

（2）当α=0.8时，系统（1）为Lü混沌系统，

应用于响应系统（3）中，仿真结果如图2所示：

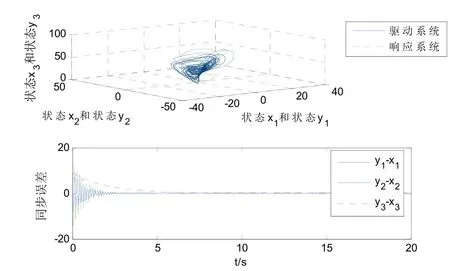
图2 三维同步相位图及同步误差图

（3）当α=0.25时，系统（1）为Lorenz混沌系统，由（2）式知根据（6）式可求解得将控制器（7）

应用于响应系统（3）中，仿真结果如图3所示：

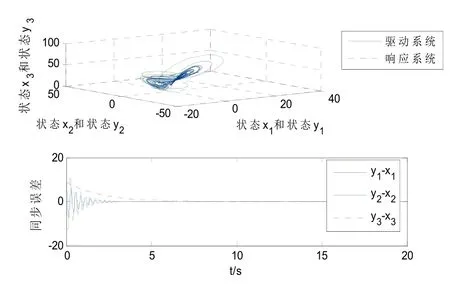
图3 三维同步相位图及同步误差图

从图1、图2和图3的仿真结果可以看出，本文提出的同步控制方法均可在较短的时间内使驱动-响应混沌系统达到同步状态，验证了该控制算法的有效性．

5 结 论

本文通过求解线性矩阵不等式，将求解得到的矩阵K应用于同步控制器中，利用Lyapunov稳定性理论证明了该方法的正确性，最后的数值仿真证明了该方法的有效性．该方法与其他的同步控制算法相比，设计的控制器简单易于操作，运算量小，可以满足实时性的需求，特别在保密通信中具有一定的使用价值．同时，该方法也适用于任何可以被改写成矩阵形式的混沌系统同步，具有较好的应用前景．

[1]Pecora L M, Carrol T L, Synchronization in chaotic systems[J]. Physical Review Letters, 1990. 821–824.

[2]Ott E, Grebogi C, Yorke J. A.. Controlling chaos[J]. Physic Review Letter, 1990. 1196-1199.

[3]Tanaka K, Ikeda T, Wang H O. A unified approach to controlling chaos via an LMI-based fuzzy control systems[J]. IEEE Trans. On Circuits and Systems, 1998. 1021-1040.

[4]Laoye J A, Vincent U E, Kareem S O. Chaos control of 4D chaotic systems using recursive backstepping nonlinear controller[J]. Chaos, Solitons and Fractals, 2009. 356-362.

[5]Aghababa M P. Robust stabilization and synchronization of a class of fractional-order chaotic systems via a novel fractional sliding mode controller[J]. Communications in Nonlinear Science and Numerical Simulation, 2012. 2670-2681.

[6]王银河，等.基于自适应模糊逻辑系统的一类混沌系统同步控制[J].控制与决策，2013（9）.

[7]刘超，王俊年，唐婷婷.Chen混沌系统的滑模同步控制方法[J].计算机工程，2011（22）.

[8]Alasty A, Salarieh H. Nonlinear feedback control of chaotic pendulum in presence of saturation effect[J]. Chaos, Solitons and Fractals, 2007. 292-304.

[9]Qi D, Liu M, Qiu M, Zhang S. Exponential H(infinity) synchronization of general discrete-time chaotic neural networks with or without time delays[J]. IEEE Trans on Neural Networks, 2010. 1358-1365.

[10]张付臣，杨洪亮.线性反馈控制在保密通信中的应用[J].计算机工程，2011（14）.

[11]李国华.基于混沌导频信号同步控制的混沌保密通信[J].计算机应用研究，2011（1）.

[12]Chen B, Liu X P, Tong S C. Adaptive fuzzy approach to control unified chaotic systems[J]. Chaos, Solitons and Fractals, 2007. 1180-1187.

[13]Slotine J E. Applied Nonlinear Control[M]. Englewood Cliffs, America New Jersey: Prentice Hall, 1991.

（责任编辑：于开红）

Synchronization Control and Simulation for a Type of Chaotic System Based on LMI Technique

GAO Zilin XIONG Jiang LUO Weimin YAN Pei
(School of Computer Science and Engineering, Chongqing Three Gorges University, Wanzhou Chongqing 404100)

For a type of chaotic system, synchronous controller is designed based on linear matrix inequality (LMI), and can make each state of chaotic systems to reach synchronization status quickly. With this method, only matrix K needs to be solved, so computation amount is very small, and can meet the requirements of real-time property in industry, and has some feasibility and validity.

chaotic systems; synchronous controller; LMI

G812.78

A

1009-8135（2015）03-0053-03

收·稿日期：2015-03-02

高子林（1986-），男，重庆万州人，助教，硕士，主要研究领域为复杂系统控制．熊 江（1969-），男，重庆万州人，教授，硕士研究生导师，主要研究领域为信息安全．罗卫敏（1977-），男，重庆万州人，高级实验师，硕士，主要研究领域为网络与信息安全．鄢 沛（1976-），男，四川营山人，高级实验师，硕士，主要研究领域为网络设计．

重庆市教委科学技术研究项目（KJ131108）；重庆三峡学院科学研究项目资助（14QN30）阶段性成果