孤子脉冲在光子晶体光纤中的传播特性研究

余先伦 高微冬 屈 勇

（重庆三峡学院信息与信号处理重点实验室，重庆万州 404100）

孤子脉冲在光子晶体光纤中的传播特性研究

余先伦 高微冬 屈 勇

（重庆三峡学院信息与信号处理重点实验室，重庆万州 404100）

根据光脉冲在光子晶体光纤中传播的非线性薛定谔方程，分析了孤子传播基本原理，给出了光脉冲在光子晶体光纤中色散和非线性效应的表达式，对非线性薛定谔方程进行归一化处理并求解，获得光子晶体光纤中基态孤子解．在远大于光纤零色散波长区域，使色散和非线性效应达到平衡，在光子晶体光纤中就可以得到稳定的光学孤子．光子晶体光纤中产生的孤子可以作为光孤子通信的载波，是光子晶体光纤中高次谐波产生的泵浦源．

光纤光学；光子晶体光纤；光学孤子

1 光脉冲在PCF中传播方程

在PCF中激光脉冲传播理论分析基于非线性Schrödinger方程

文献表明，通过对PCF空气孔尺寸和排列进行设计，改变PCF色散特性，使PCF中群速度色散和三阶色散的取值可以远超过高阶色散，而PCF非线性效应中考虑高频脉冲对材料折射率的影响，光场沿长度方向偏振态保持不变，非线性响应是瞬时作用，则非线性Schrödinger方程（1）可以简化为

其中：D2，D3表示PCF的二阶色散和三阶色散．方程（2）表明，在PCF中很好设计圆孔的尺寸和孔间距，使PCF中色散和非线性达到平衡，在PCF中就可以产生孤子脉冲．

2 PCF非线性效应

在PCF中，折射率的非线性变化小于10-6，脉冲的偏振方向可以认为不变，电场振幅可以采用标量近似，如果光脉冲中心频率在ω0，光谱宽度为Δω，在慢变包络近似下，PCF的非线性响应是瞬时的，则脉冲引起的PCF非线性极化强度可表示为：

其中ω0真空中介电常数，而三阶极化率．PCF非线性折射率×3/8×n0，n0熔硅的折射率．

在PCF中，因为高频激光脉冲的影响，会引起PCF非线性折射率的改变，其改变量可表示为Δn= n2|E（z，t）|2，非线性折射率的改变在PCF中会产生强烈的非线性效应，PCF中非线性响应系数可采用下式表示．

其中，n2是PCF非线性折射率，c是真空中光速是PCF有效模场面积，可表示为

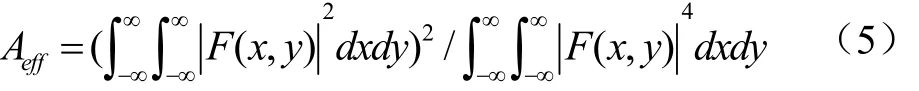
F（x，y）是PCF中横向场分布函数．

在方程（1）中，PCF延迟非线性效应响应函数R（t）标准形式是

（6）式中fR表示拉曼响应，在光纤中取值是确定的，可取0.18，δ（t）和K（t）是delta和Heaviside阶跃函数，τ1，τ2表示脉冲在PCF的展宽．

3 PCF中色散效应

在PCF中，光脉冲传播速度与频率相关，色散在PCF光脉冲传播时有着关键作用．在频域中，PCF色散效应可以通过中心频率处展开为模的传播常数的Taylor表示．

在PCF中色散效应一般考虑到二阶和三阶色散D2，D3，D2=d2β/dω2即群速度色散．在PCF中定义色散长度和非线性长度其中p0和τ0是初始脉冲的功率和脉宽，色散长度和非线性长度的比值

在PCF中，如果色散长度远大于非线性长度时，色散效应是PCF中光脉冲传播特性中起作用的主要因素，在非线性薛定谔方程中非线性项可以忽略，如果非线性长度远大于色散长度，则PCF中将表现出强烈非线性效应，如果当PCF中色散长度与非线性效应长度可以比拟时，在PCF中将会产生孤子脉冲．在PCF中因为色散和非线性效应的影响，脉冲传播的相位会产生漂移，其最大相位漂移量可定义为是PCF有效长度，可以定义为实际长度，α传播损耗．

假定耦合进PCF中的光脉冲是一个正弦包络脉冲，PCF输出脉冲强度仍是一个同样的包络，群速度色散可表示为：

GDx（λ）和GDy（λ）是x和y方向偏振态的群时延，θ表示PCF快轴与入射光脉冲偏振方向的夹角，PCF中任意方向的群速度色散都是在两个偏振方向上的叠加，PCF中两个偏振方向群速度色散之差ə2（βx-βy）/əω2=ə/əω（Δng/c），Δng是两个偏振方向上群速度之差．根据PCF的标准参数，根据（8）式可以得到PCF中不同入射光脉冲波长下的群速度色散值，如图1所示．

4 PCF孤子解及传播特性

PCF中入射的飞秒激光脉冲波长如果大于PCF的零色散波长，在反常色散区域，群速度色散是取负值，PCF中就可以保持光学孤子．对方程（2）进行归一化处理，令其中p0和τ0是初始脉冲的功率和脉宽，方程（2）的归一化方程为

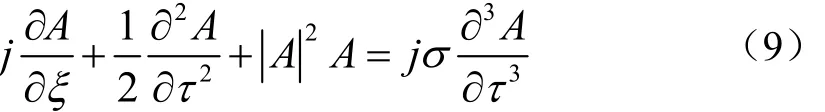
光脉冲在PCF中传播，光纤材料存在二阶色散和三阶色散，如果三阶色散值与二阶色散值相比较是相对较弱的，则三阶色散项可作为微扰处理．脉冲在PCF中稳定传播形成孤子，它要求群速度色散和非线性效应要达到一个动态的平衡，群速度色散和非线性效应的差值也必须在零附近波动，方程（9）就是一个带微扰的非线性Schrödinger方程，它具有孤子解．对方程（9）求解，其基态孤子解可表述为：

其中η，η，δ，φ是代表孤子脉冲的孤子振幅、位置、载频和相位四个参量，它们都与ξ有关．选取PCF的典型参量值，根据公式（10），作出的PCF传播孤子图如图2所示.

5 结 论

在PCF中只有效控制PCF的色散和非线性效应的取值，当入射光脉冲波长远大于零色散波长，光脉冲传播就会处于反常色散区域，在PCF中就会产生光学孤子，这在国际上已经经过实验证实．在多模PCF光纤中孤子的中心频率因为Raman效应经历连续转换，处于在光子晶体光纤反常色散区域中传播的耦合孤子，因为光纤材料延迟的光学非线性，孤子当它们通过光纤传播时经历一个连续的频率下转换，即孤子自平移现象，PCF高的光学非线性能增强这种效应，可以制作有效紧致光纤频率转换器，光学孤子的中心波长在红外区域，即产生红移孤子，红移孤子可以是三次谐波的泵浦源．同时在PCF中产生光学孤子可以为光纤通信、光孤子通信提供新的理论基础和实践可能性．

图1 光纤入射光脉冲不同偏振态时的群时延

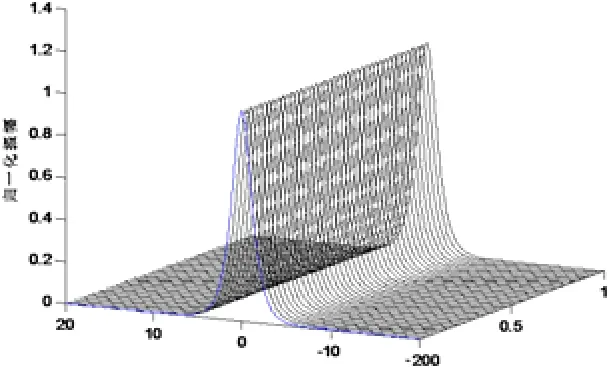
图2 PCF中传播的光学孤子

[1]Wojtek J.Bock,Tinko A.Eftimov,Predrag Mikulic et al.,An inline core-cladding intermodal interfereometer using a photonic crystal fiber，J.Lightw.Technol.,2009(17):3933-3939.

[2]Vincent Laude,Abdelkrim Khelif,Sarsh Benchabane et.al.，Photonic band-gap guidance of acoustic modes in photonic crystal fibers，Phys. Rev.E 71,045107(2005).

[3]Takashi Matsui,Kazuhide Nakajima,C.Fukai.，Applicability of photonic crystal fiber with uniform air-hole structure to high-speed and wide-band transmitsion over conventional telecommunicateion，J.Lightw.Technol.,2009(23):5410-5416.

[4]Beaudou B.,Bhardwaj A.,Bradley T.D.,et.al.,Macro Bending Losses in Single-Cell Kagome-Lattice Hollow-Core Photonic Crystal Fibers , J.Lightw.Technol.,2014(7):1370–1373.

[5]Feng Zhou, Sun-Jie Qiu,Wei Luo,et.al.,An All-Fiber Reflective Hydrogen Sensor Based on a Photonic Crystal Fiber In-Line Interferometer , Sensors Journal, IEEE ,2014(4):1133–1136.

[6]Ming Deng,Xiaokang Sun,Huifeng Wei,et.al.,Photonic Crystal Fiber-Based Modal Interferometer for Refractive Index Sensing , IEEE Photon. Technol.Lett.,2014(6):531–534.

[7]Tiwari V.S.,Khetani A.,Momenpour A.,Optimum Size and Volume of Nanoparticles Within Hollow Core Photonic Crystal Fiber, IEEE Journal of Selected Topics in Quantum Electronics,2014(3):7300608.

（责任编辑：于开红）

A Research of the Optics Solitary Pulse Transmission in Photonic Crystal Fiber

YU Xianlun GAO Weidong QU Yong
(Key Laboratory of Signal and Information Processing, Chongqing Three Gorges University, Wanzhou Chongqing ,404100)

According to the nonlinear Schrodinger equation of the optical pulse propagation in photonic crystal fiber, it is analyzed that the basic principle of soliton, the optical pulse expression, is given that the dispersion and nonlinear effects in photonic crystal fiber, the nonlinear Schrodinger equation, is normalized, and the ground state soliton solution is obtained in the photonic crystal fiber. In the wavelength region far greater than the fiber zero dispersion, the balance between the dispersion and nonlinear effects in photonic crystal fibers is achieved, and the stable optical soliton can obtained. The generation of soliton in photonic crystal fiber can be used as carrier of optical soliton communication, and is the pumping source in high order harmonic generation in photonic crystal fiber.

fiber optics; photonic crystal fiber; optics soliton

G812.78

A

1009-8135（2015）03-0047-03

2015-02-10

余先伦（1967-），男，重庆梁平人，重庆三峡学院教授，主要研究光纤通信、光纤传感等．高微冬（1992-），女，陕西渭南人，重庆三峡学院硕士研究生，主要研究光子晶体光纤和传感器等．

重庆市教委自然科学基金项目（编号KJ131121和KJ1401026）阶段性成果