一种新的求解CQSDP的全-Newton步内点算法
2015-06-27张明望
李 鑫 季 萍 张明望
(三峡大学理学院,湖北宜昌 443002)
一种新的求解CQSDP的全-Newton步内点算法
李 鑫 季 萍 张明望*
(三峡大学理学院,湖北宜昌 443002)
对凸二次半定规划提出了一种新的全-Newton步原始-对偶内点算法.通过建立和应用一些新的技术性结果,证明了算法的迭代复杂性为这与目前凸二次半定规划的小步校正内点算法最好的迭代复杂性一致.
凸二次半定规划;内点算法;全-Newton步;迭代复杂性
1 引 言
本文讨论如下标准形式的凸二次半定规划(CQSDP)原始问题及其对偶问题.
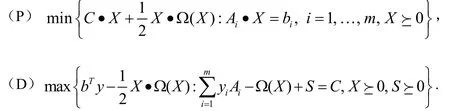
其中:C, Ai∈Sn且假设矩阵Ai, i=1,…,m线性无关,b∈Rm.Ω(X)是Sn→Sn上的一个自共轭半正定线性算子,即对任意的A, B∈Sn,有Ω(A)·B=A·Ω(B),Ω(A)·A≥0.为了方便起见,我们类似于文献[1,2],考虑如下特殊的情况,
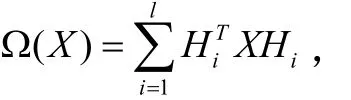
其中,Hi是Rn×n上的矩阵,l为小于或等于n2的整数.
CQSDP是半定规划(SDP)的推广,它在求解欧几里德距离矩阵问题[3]、最近相关矩阵问题[4]中有重要的应用.近些年来,关于CQSDP的研究,已取得一系重要的成果,详细研究见文献[1,2,5].2003年,Darvay[6]提出了一种基于新的搜索方向(Darvay方向)求解线性规划(LP)的原始-对偶路径跟踪内点算法,并证明了算法的迭代复杂性为2006年,Roos[7]对线性规划提出了一种全-Newton步不可行内点算法,并得到了算法的迭代复杂性为2009年,Wang等[8]将Darvay提出的算法[6]推广到SDP模型中,并得到了与文献[6]同样好的迭代复杂性.2014年,Ahmadi等[9]对线性规划提出了一种基于Darvay方向的全-Newton步不可行内点算法,并得到了算法的迭代复杂性为同年,Wang等[10]提出了一种求解() *P k线性互补问题的全-Newton步可行内点算法,得到了算法迭代复杂性为
受其工作的启发,本文提出了一种新的求解CQSDP的全-Newton步原始-对偶内点算法.由于算法中迭代方向的非正交性,导致相应算法的分析有别于LP和SDP的情形.通过建立和应用一些新的技术性结果,我们证明了算法的迭代复杂性结果为这与目前CQSDP的小步校正内点算法最好的迭代复杂性一致.
本文采用如下记号:A·B=Tr(AB)表示矩阵A与B的内积分别表示对称,对称半正定和对称正定的n×n矩阵集合.R表示实数集,Rm表示m维向量空间,Rn×n表示n×n实矩阵集合.符号和分别表示矩阵X是半正定对称矩阵和正定对称矩阵.和分别表示矩阵V的特征值,最小特征值和最大特征值.X=diag(x)表示由向量x的分量构成的对角矩阵X.F-范数表示为||·||F,E表示n×n单位矩阵.符号A~B表示矩阵A与矩阵B相似,即存在可逆矩阵Z,使得A=ZBZ-1.如果f(x)≥0是一个实值函数,那么f(x)=O(x)表示存在正实数c,使得()f xcx≤.
2 预备知识
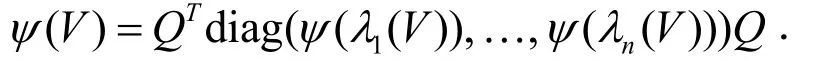
2.1 中心路径
不失一般性,假设问题(P)和(D)满足内点算法条件[11],即存在满足

若(X,y,S)是问题(P)和(D)的可行解,则由对偶理论知,(X,y,S)是问题(P)和(D)的最优解的充要条件为:
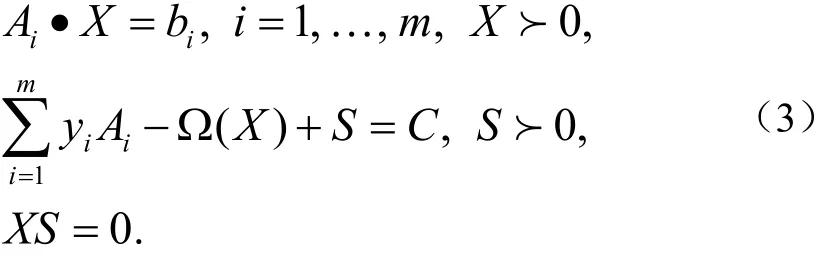
根据原始-对偶内点算法的基本思想,用参数方程XS=μE(μ为正实数),来代替系统(3)中的第三个等式(互补条件),得到如下系统:
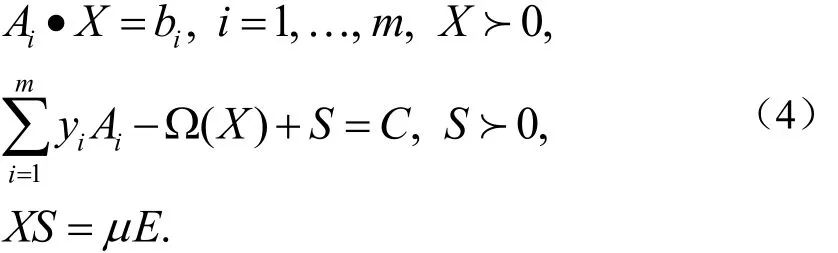
由文献[12]知,若问题(P)和(D)满足内点条件,则对任意的μ>0,系统(4)有唯一解(X(μ),y(μ),S(μ)),称X(μ)为问题(P)的μ-中心,(y(μ),S(μ))为问题(D)的μ-中心.μ-中心组成的集合(X(μ),y(μ),S(μ))形成了一个同伦路径,称之为问题(P)和(D)的中心路径.当μ→0时,中心路径的极限值存在.又因为此极限值满足互补条件,故此极限点即为问题(P)和(D)的最优解.
2.2 迭代方向
类似于SDP的情形[8],本文用来代替XS=μE,其中()ψ·是[0,)+∞上的可导实值函数,则系统(4)可写成:
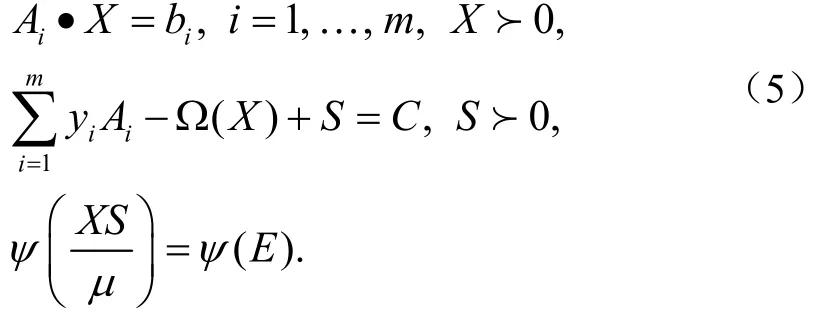
对系统(5)运用牛顿法,得

应用文献[8]中引理2.5并忽略ΔXΔS项,有
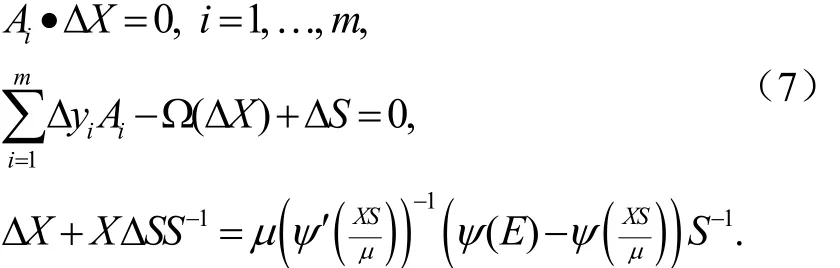
从系统(7)中容易看出,虽然ΔS是对称的,但ΔX不一定对称.为了使得ΔX对称,本文采用NT对称化策略[11].
定义
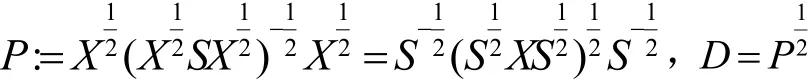
则矩阵D可以将矩阵X,S尺度化,使之成为同一个对称正定矩阵V,即

于是,我们有
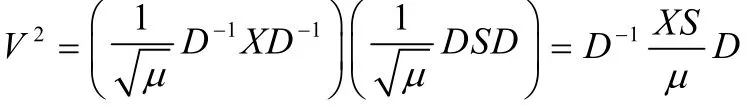
根据定义1,有
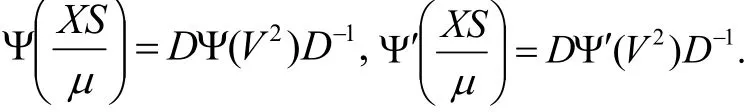
进一步,定义

这样,系统(7)等价于
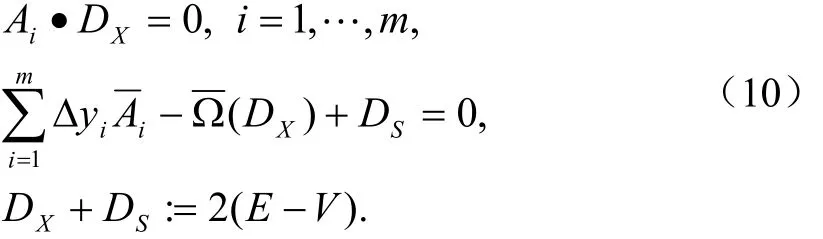
由于矩阵Ai线性无关及问题(P)和(D)满足内点条件,所以对任意μ>0,系统(10)存在唯一解(DX,Δy,DS)[12]250.再应用(9)式便可得到算法的迭代方向(ΔX,Δy,ΔS).
不难看出,若(X,y,S)≠(X(μ),y(μ),S(μ)),则(ΔX,Δy,ΔS)≠(0,0,0).沿此方向取全步长,得到新的迭代点,

又因为()XΩ是自共轭半正定算子,所以
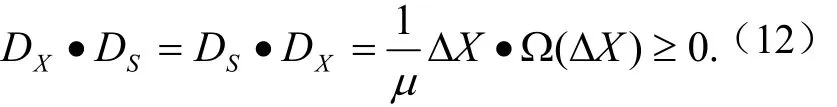
注1:在LP和SDP情形中[6-9],DX·DS=0,即DX与DS正交,由(12)式可知,对于CQSDP的情形,DX与DS不再正交,这正是本文新算法与SDP相应算法及其分析的主要不同之处.
在算法分析中,我们引入一个邻近度量δ(V),其定义为:
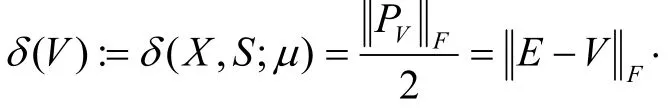
容易验证,(,,)X Sδμ当且仅当V=E,当且仅当XS=μE.
3 CQSDP的全-Newton步原始-对偶内点算法
CQSDP的全-Newton步原始-对偶内点算法的基本框架如下图1.下一部分我们将证明该算法是良定义的.
Input:
阈值参数01τ<<;精度参数0ε>;
障碍校正参数θ,01θ<<;
严格初始可行点(X0,y0,S0),μ0=1使得

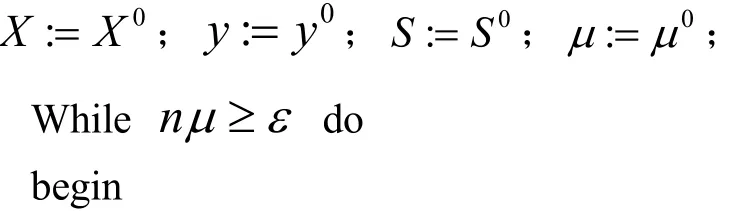
求解系统(10),再应用(9)得到算法的迭代方向(ΔX,Δy,ΔS );
更新(X, y, S):=(X, y, S)+(ΔX,Δy,ΔS );
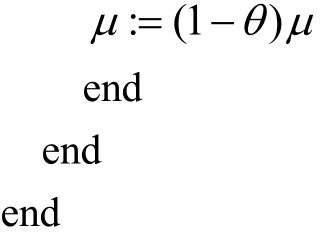
图1 算法
注2:在算法的复杂性分析中,阈值参数τ和障碍校正参数θ的选取也是至关重要的.通常,如果θ是一个与问题规模n无关的常数,例如那么称相应的算法为大步校正算法.如果θ的选取依赖于问题的规模n,例如那么称相应的算法为小步校正算法.
4 算法分析
首先,我们引入记号QV:=DX-DS,则
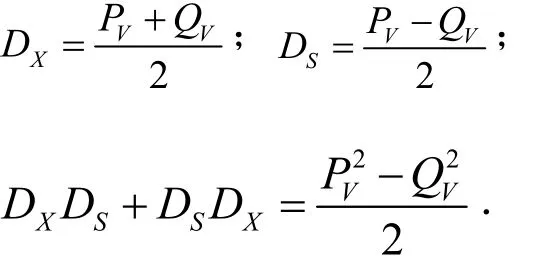
由(12)式,得
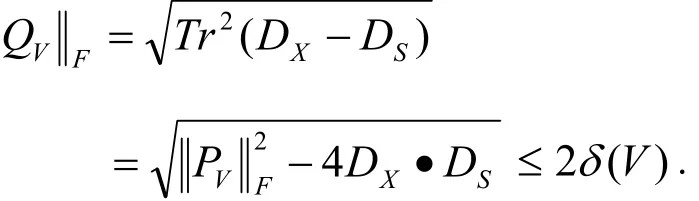
引理2 ([8]引理6.3) 如果δ:=δ(X, S;μ)<1,那么全-Newton步是严格可行的.
引理3 ([8]引理6.4)如果δ:=δ(X, S;μ)<1,
下面给出几个重要的引理.
那么
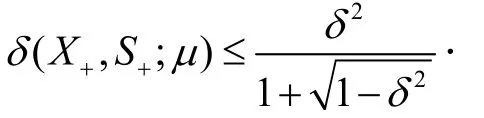
引理4 ([8]引理6.5)经过一次全-Newton步迭代后,有
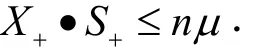
引理5 ([8]引理6.6)如果δ:=δ(X, S;μ)<1,μ+:=(1-θ) μ,其中0<θ<1,那么
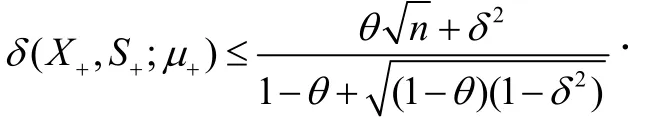
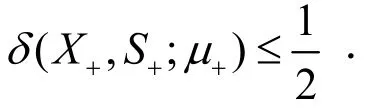
引理6 假设Xk,Sk是新算法第k次迭代生
成的迭代点且μ:=μk,则当
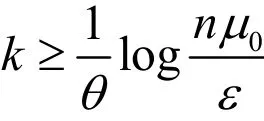
时,有kkXSε·≤.
证明 由引理4,知
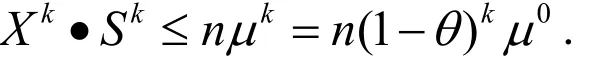
要使不等式kkXSε·≤成立,则只需证
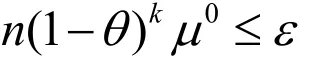
成立.对上式两边取对数,得
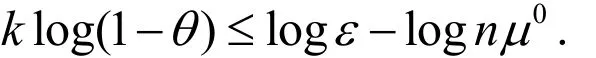
又因为,当01θ<<时,log(1)θθ --≥.所以有两边同除以θ,即引理得证.

[1]Wang G Q,Bai Y Q.Primal-dual Interior-point Algorithm for Convex Quadratic Semi-definite Optimization [J].Nonlinear Analysis:Real World,Applications,2009,71:3389-3402.
[2]Zhang M W.A Large-update Interior-point Algorithm for Convex Quadratic Semi-definite Optimization Based on A New Kernel Function [J].Acta Mathematica Sinica,English Series,2012,28(11):2313-2328.
[3]Aifakin A Y,Khandani A,Wolkowicz H.Solving Euclidean Distance Matrix Completion Problem Via Semi-definite Programming [J].Computation Optimization and Applications,1999,12:13-30.
[4]Qi H,Sun D.A Quadratically Convergent Newton Method for Computing the Nearest Correlation Matrix [J]. SIAM Journal of Matrix Analysis and Application, 2006,28:360-385.
[5]Achache M,Guerra L.A Full-Nesterov-Todd-step Feasible Primal-dual Interior-point Algorithm for Convex Quadratic Semi-definite Optimization [J]. Applied Mathematics and Computation,2014,231:581-590.
[6]Daravy Z.New Interior-point Algorithms in Linear Optimization [J].Advanced Modeling Optimization,2003,5(1):51-92.
[7]Roos.C. A Full-Newton Step O(n) Infeasible Interior-point Algorithm for Linear Optimization [J].SIAM Journal on Optimization,2006,16(4):1110-1136.
[8]Wang G Q,Bai Y Q.A New Primal-dual Path-following Interior-point Algorithm for Semi-definite Optimization [J].Journal of Mathematical Analysis and Applications,2009,353:339-349.
[9]Ahmadi K,Hasani F,Behrouz K.A Full-Newton Step Infeasible Interior-point Algorithm Based on Darvay Directions for Linear Optimization [J]. Journal of Mathematics Modeling and Algorithms,2014,12:191-208.
[10]Wang G Q,Fan X J,Zhu D T. New Complexity Analysis of A Full-Newton Step Feasible Interiorpoint Algorithm for P*(k)-LCP [J]. Optimization Letters,2014,DOI 10.1007/s11590-014-0800-4.
[11]Nesterov Y E,Todd M J. Self-scaled Barriers and Interior-point for Convex Programming [J]. Mathematics of Operations Research,1997,22(1):1-42.
[12]Klerk E D. Aspects of Semi-definite Programming:Interior Point Algorithms and Selected Applications [M].Kluwer Academic Publishers,Dordrecht,The Netherlands,2002.
(责任编辑:于开红)
A New Full-Newton Step Interior-point Algorithm for Convex Quadratic Semi-definite Programming
LI Xin JI Ping ZHANG Mingwang
(School of Science, Three Gorges University, Yichang Hubei 443002)
In this paper, we propose a new full-Newton step primal-dual interior-point algorithm for solving convex quadratic semi-definite programming. By establishing and using new technical results, we show that the iteration complexity of algorithm asis as good as the currently best iteration complexity for small-update interior-point algorithms of convex quadratic semi-definite programming.
convex quadratic semi-definite programming; interior-point algorithm; full-Newton step; iteration complexity
G812.78
A
1009-8135(2015)03-0031-06
2015-02-25
李 鑫(1989-),男,甘肃武威人,三峡大学硕士研究生,主要研究最优化理论与应用.季 萍(1989-),女,湖北武汉人,三峡大学硕士研究生,主要研究最优化理论与应用.
张明望(1959-),男,湖北宜昌人,三峡大学教授,主要研究最优化理论及应用.
国家自然科学基金(71471102)阶段性成果
