基于颜色和空间信息的多特征融合目标跟踪算法

许婉君，侯志强，余旺盛，张 浪

引言

目标跟踪是当前计算机视觉领域研究的热点课题之一，在各个领域有着广泛的应用，如导弹防御系统、智能导航、人机交互等［1－3］。基于多特征融合的跟踪更是近年来研究的热点，它考虑目标多方面的信息，以使跟踪更鲁棒更稳定。

目标特征的表示方法对跟踪性能有很重要的影响［4］，通常采用的特征包括颜色、纹理、边缘、运动等［5］。其中颜色特征以其对目标部分遮挡和旋转的鲁棒性强以及尺度不变等特性，被广泛用于目标跟踪［6］。文献［7］采用经典的 Mean Shift算法，利用核函数加权的颜色直方图建立颜色模型，该方法实现简单，但该颜色模型将整个颜色空间进行均匀剖分，弱化了对目标颜色分布的描述能力，且当目标和背景相似程度较大时容易造成跟踪的不稳定。如果粗略地表达目标的颜色分布，算法的跟踪速度会提高，然而由于无法准确地刻画目标的颜色密度，很容易导致跟踪误差增大甚至跟踪失败。对此，文献［8］提出一种改进的Mean Shift跟踪算法，建立一种新的颜色模型，对目标颜色进行聚类分析，根据聚类结果通过矩阵分解和正交变换自适应地剖分目标的颜色空间，从而确定对应于每一个聚类的子区间。该颜色模型比经典的Mean Shift算法具有更好的性能，但理论推导和计算复杂。文献［9］提出的颜色纹理改进算法在跟踪速度和跟踪性能上均比颜色直方图表示法有显著提高，但在实现时丢失了部分颜色信息，损失了一定的描述能力。此外，当被跟踪的目标发生旋转、位姿变化或背景中出现相似颜色干扰时，由于缺少空间信息，仅利用颜色特征对目标跟踪的效果不佳。文献［10］提出一种用空间直方图信息的目标跟踪算法，空间直方图与传统的颜色直方图相比，包含了目标的空间信息，能够更加有效地描述目标颜色特征。

对此，本文提出一种基于自适应颜色直方图的多特征融合目标跟踪算法。采用自适应颜色直方图作为目标颜色模型，根据目标颜色分布自适应地划分颜色直方图区间。同时，引入空间直方图作为目标跟踪的第二特征。在粒子滤波框架下采用文献［11］提出的融合策略实现对目标的跟踪。实验结果表明，算法在目标表示和跟踪性能上均有所提高。

1 粒子滤波与目标特征的不确定性

1.1 粒子滤波跟踪框架

粒子滤波又称为蒙特卡洛滤波，它通过非参数的蒙特卡洛模拟方法来实现递推贝叶斯滤波，它的有效性主要表现在适用于处理非高斯、非线性的滤波问题［12］。其基本原理是假设动态系统可以用以下的状态空间模型表示：

式中：xk表示系统状态向量；zk表示量测向量；vk－1、wk为独立同分布的系统噪声和观测噪声。根据贝叶斯滤波的基本原理，有下面2种情况。

预测：

更新：

然而，通常状态的概率密度函数（PDF）是未知的，这 时 需 要 从 一 个 容 易 采 样 的 权 值 q（x0：k／z1：k－1）中独立抽取 N 个样本｛x（i）0：k，i＝1，…，N｝，状态的PDF逼近为

然而，由于粒子滤波存在随机性，使其对目标定位存在一定的误差。对此，文献［11］根据粒子分布情况的不同，定义了一种目标特征的不确定性度量，以减小这种随机性带来的误差，使跟踪更加准确。本文算法也用到了这种特征的不确定性度量方法。

1.2 目标特征的不确定性

在目标跟踪过程中，每种目标特征对不同场景目标位置估计的准确度是不一样的，为了描述每种目标特征在目标跟踪过程中的不确定性，文献［11］提出一种自适应的目标特征不确定性度量：

式中：Uik表示k时刻第i种特征的不确定性；vark是时刻k所有粒子空间位置的方差，表示粒子空间分布的分散程度。vark＝tr（∑），∑表示粒子2个位置坐标的协方差矩阵，var越大，粒子的空间位置越分散；pi为似然函数，即观测概率值，为第i种特征对应的目标模板与候选模板的Bhattacharyya系数；H（pit）是时刻k第i种特征下所有粒子观测概率值的熵，表示观测概率值在粒子上的分散程度。在信息论中，熵是不确定性的量度［12］：

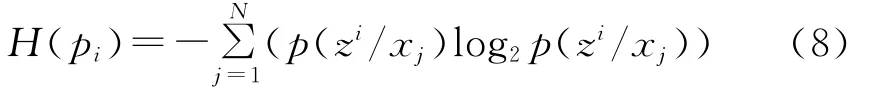
式中H（pi）值越小，表示目标第i种特征对目标位置估计的准确度越高。

由（8）式可知，特征的不确定性既包含了粒子的空间位置信息，又表征了似然函数pi的尖锐程度。k时刻，粒子分布越集中，vark越小，不确定性越小，反之不确定性越大。而对似然函数来说，似然函数的尖锐程度越高，说明该特征的鉴别能力越强，不确定性越小，反之亦然。

2 基于多特征的目标跟踪算法

本节分别给出目标颜色特征和空间直方图特征的的提取方法，以及2种特征目标模型与候选模型相似度的计算方法，并由此给出特征融合策略。

2.1 目标的多特征描述

2.1.1 颜色分布模型

针对传统颜色直方图均匀划分颜色空间造成许多空的直方图且不能准确表达目标颜色分布的缺点，本文在文献［8］提出的颜色模型的基础上，提出一种自适应颜色直方图的方法，即根据目标的颜色分布自适应地划分颜色区间，以获取目标更准确的颜色模型。

如图1所示，m为累积直方图曲线。y轴表示归一化的均匀划分的像素颜色刻度值，范围为［0，1］，x轴表示自适应非均匀划分的颜色值刻度，范围为［0，255］。这里以4个区间的直方图为例。首先将y轴均匀划分为4个区间［0，A1］、［A1，A2］、［A2，A3］、［A3，A4］，然后通过曲线m 将A1、A2、A3、A4映射到x轴上的B1、B2、B3、B4，得到直方图划分对应的刻度。

输入视频到计算机后，在首帧图像中利用上述方法确定刻度，即可得到自适应非均匀划分的特征区间，区间大小表征了颜色分布的集中程度。在后续的跟踪中，根据确定的直方图区间刻度对目标模板进行直方图统计，即可得到自适应颜色直方图。

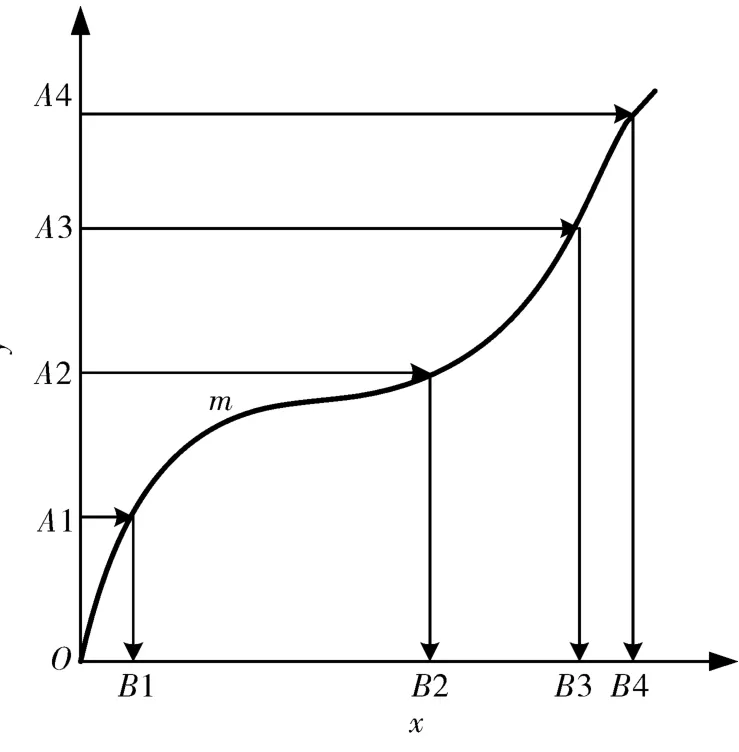
图1 一种自适应划分颜色直方图的方法Fig.1 Adaptive approach for selecting color histogram

如图2所示，（a）和（b）分别为传统颜色直方图和自适应颜色直方图对三维颜色空间的划分结果，x，y，z分别表示三维颜色空间的坐标轴。前者将颜色空间均匀划分，而后者对颜色分布相对集中的区域，划分较多的“窗格”，即颜色区间（也就是说，每个“窗格”空间相对较小），以突出该区域的颜色分布。反之，在颜色分布相对分散的区域，划分较少的“窗格”。

图2 2种划分三维颜色空间的方法Fig.2 Two methods for distributing 3D color space

自适应颜色直方图根据目标的颜色分布，对颜色空间进行非均匀划分，能够更加准确地描述目标颜色特征，相比空间直方图具有明显的优势。

2.1.2 空间直方图模型

空间信息在目标跟踪中也起着重要的作用。二阶空间直方图不但计算了像素颜色特征的频率，还统计了直方图中每个区间中所有像素对应坐标的均值和协方差，在目标跟踪中表现了很好的性能［10］。

图像的二阶空间直方图［10］可表示为

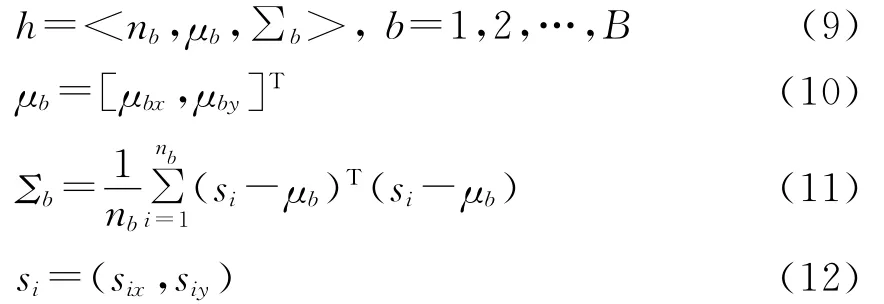
式中：nb是像素值落入第b个单元的像素总数；μb和∑b分别是这些像素点的坐标均值向量和协方差矩阵；B是单元总个数。

2.2 多特征的相似性度量

对于目标的多特征描述，如果直接将目标的多个特征组合在一起，那么随着特征空间维数的增加，运算量会大大增加［12］。因此本文分别建立自适应颜色直方图模型与空间直方图模型来描述目标，以降低特征维数。

2.2.1 自适应颜色直方图相似性度量

颜色特征对应的目标模板与候选模板：

目标模板Q＝｛＾qu｝u＝1，…，N

候选模板P＝｛＾pu｝u＝1，…，N

得到候选模板与目标模板后，二者之间的相似度可采用Bhattacharyya距离［13］来描述：

式中ρ越大，表示候选模板与目标模板越相似。Bhattacharyya距离：

2.2.2 空间直方图相似性度量

两空间直方图h＝＜nb，μb，∑b＞和h′＝＜n′b，μ′b，∑′b＞的相似度ρ（h，h′）可表示［14］为

式中权值ψb取自高斯分布（x′b，∑′b），表示空间相似程度［15］：

2.3 特征融合策略

根据文献［11］中提出的融合策略，在假设n种观测特征是条件独立的情况下，将每种特征的观测概率值加上一个正比于该特征不确定性的均匀分布，作归一化处理后，再取乘积，表达式如下：

若n取2，则有融合规则：

式中：U1，U2分别表示颜色和空间直方图特征对应的不确定性；U（x）是一个离散的均匀分布，设粒子数为N，则U（x）＝1／N。这里的观测概率值即为特征目标模板与候选模板之间的相似度。

2.4 算法步骤

综上所述，算法流程如图3所示，主要步骤如下：

1）初始化。初始时刻（k＝0），手动选取目标，利用自适应颜色直方图得到非均匀划分的特征区间，提取目标模板颜色特征直方图q10，同时提取空间直方图q20，从先验分布中抽取N 个初始粒子，权值均设为｛ωi0｝iN＝1＝1／N；

2）状态预测。在时刻k（k＞0），根据状态转移模型xk＝Axk－1＋Nk和粒子xk－1，预测粒子xk的状态；

3）计算粒子空间位置方差vark和2种特征的概率熵。由目标矩形框内粒子位置坐标计算vark，由（13）式和（17）式分别计算2种特征目标模板与候选模板之间相似度，即似然函数p（z1／x），p（z2／x），从而得到2种特征的概率熵H（p11）和 H（p21）；

4）计算特征不确定性。由3）中得到vark和H（p11），H（pt2）根据（7）式分别计算颜色特征不确定性U1和U2；

5）状态更新由（19）式得到特征融合后似然函数p（z1，z2／x），再由ωit＝ωit－1·p（z1，z2／x）更新当前帧粒子权值，并作归一化处理；

6）重采样。根据融合后粒子权值分布决定是否重采样；

7）转回2）进行下一帧的跟踪。

图3 算法流程图Fig.3 Flow chart of our tacking algorithm

3 实验结果及对比分析

为了测试本文算法在动态场景下跟踪的鲁棒性，我们对大量视频进行实验测试，这里选取了其中4组标准测试视频序列进行实验结果展示。实验中，粒子数目设为N＝200，均匀分布U（x）＝1／N。

为了验证算法对目标描述的有效性，在融合策略一致的条件下采用文献［11］提出的算法，基于空间直方图的单一特征跟踪算法作为对比。为了验证本文算法在融合策略上的鲁棒性，在目标描述一致的条件下，采用加性融合、乘性融合算法作为对比。在跟踪性能上，采用CT［16］算法作为对比。图4是部分跟踪结果，每一帧中不同算法的跟踪结果分别采用不同颜色的实线矩形框表示，左上角为帧序号。

3.1 定性分析

1）David3序列

图4（a）为David3部分跟踪结果。在该序列中，背景变化较大，目标经历了部分遮挡，跟踪结果显示本文算法经历遮挡后仍能很好地捕捉到目标，从图中第141帧可以看出，文献［11］介绍的算法及CT算法都出现较大跟踪误差，而本文算法对目标背景变化适应性最好。

2）Basketball序列

图4（b）为Basketball部分跟踪结果。由于目标的局部背景中存在其他相似运动目标，使目标的颜色特征受到干扰，但由于目标的空间直方图特征能有效地鉴别目标，融合跟踪的性能并未受到较大影响。由第616帧可以看出，当跟踪目标经过相似运动目标时，本文算法仍能很好地跟踪目标。

3）Bolt序列

图4（c）为Bolt序列部分跟踪结果。就该序列而言，目标经历了背景颜色变化，使颜色特征可分性降低，其相应权值减小，而空间直方图特征权值增加，从而克服背景干扰的影响。从第254帧可以看出，单一特征跟踪算法和CT算法跟踪失效，本文算法跟踪性能最佳。

4）MountainBike序列

图4（d）为 MountainBike部分跟踪结果。该测试序列为室外车辆跟踪视频，目的是测试背景与目标颜色相近情况下算法的跟踪性能。由第171帧可以看出，在摩托车飞离车道时，运动速度突然加快，CT、加性融合算法跟踪失效，本文算法跟踪效果最好。

3.2 定量分析

从中心位置误差和实时性2个方面定量分析本文算法对于复杂背景下跟踪目标的鲁棒性。

3.2.1 中心位置误差比较

为了对跟踪结果进行定量分析，引入中心位置误差，该指标表示目标中心位置与真实目标中心位置之间的误差，单位为像素，其值越小跟踪精度越高，反之越低［17］。

图4 各算法跟踪结果比较Fig.4 Results comparison of 5 tracking algorithms

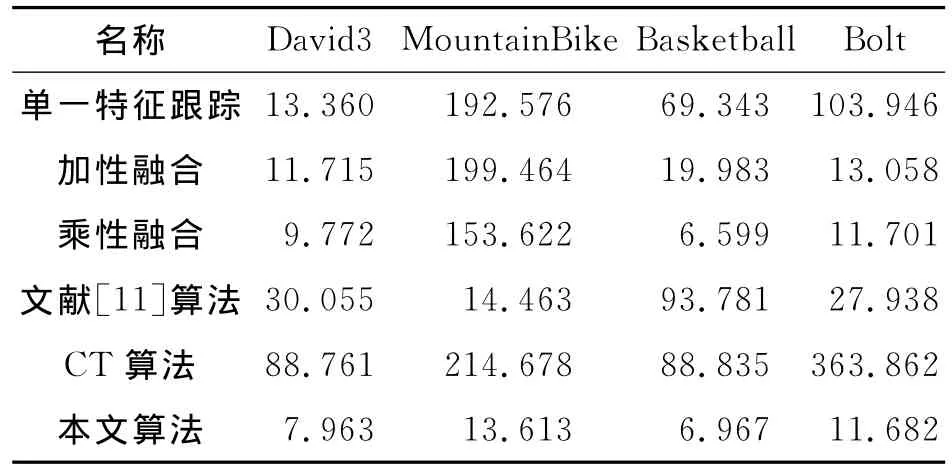
表1 平均中心位置误差比较 像素Table 1 Comparison of average center location errors

3.2.2 实时性

算法实时性方面，在未对算法作任何优化的情况下，取200个粒子，经测试，本文算法在仿真条件下能够达到平均11帧／s的运行速度。由于基于多特征融合的跟踪算法需要同时提取和处理多种特征，故运行效率上比基于单一特征的要低。若对算法进行一定的优化，跟踪速度能够得到进一步提升。

4 结束语

本研究在粒子滤波框架内，采用自适应颜色直方图和空间直方图具有一定互补性的2个特征对目标进行联合概率跟踪。该方法根据实际场景，自动调整特征权值，有效应对场景变化，避免了单一颜色特征跟踪稳定性较差的问题。通过对比各算法的平均中心位置误差可知，本文算法在序列David3，MountainBike，Bolt中分别以大小为7.963像素，13.613像素和11.682像素平均中心位置误差取得最好的跟踪精度，而在序列Basketball中平均中心位置误差为6.967像素，仅次于乘性融合算法的6.599像素。从而，验证了本文方法对场景及目标变化具有良好的适应性，能够实现鲁棒的目标跟踪。

［1］ Wu Yi，Lim J，Yang M H.Online object tracking：a benchmark［C］.Washington，D.C.：IEEE，2013：2411－2418.

［2］ Yang F，Lu H C，Yang M H.Robust superpixel tracking［J］.IEEE Transactions on Image Processing，2014，23（4）：1639－1651.

［3］ Li Wu，Hou Zhiqiang，Wei Guojian，et al.Algorithm of scale－variant objects tracking based on ellipse log－polar transform ［J］.Journal of Applied Optics，2014，35（1）：65－70.

李武，侯志强，魏国剑，等.基于椭圆对数极坐标变换的尺度变化目标跟踪算法［J］.应用光学，2014，35（1）：65－70.

［4］ Xin Yang，Cheng K T.Local difference binary for ultrafast and distinctive feature description［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2014，36（1）：188－194.

［5］ Yan Hui，Xu Tingfa，Wu Qingqing，et al.Multi－object tracking based on multi－feature joint matching［J］.Chinese Optics，2013，6（2）：163－170.

闫辉，许廷发，吴青青，等.多特征融合匹配的多目标跟踪［J］.中国光学，2013，6（2）：163－170.

［6］ Zhong Xiaopin，Xue Jianru，Zheng Nanning，et al.An adaptive fusion strategy based multiple－cue tracking［J］.Journal of Electronics ＆Information Technology，2007，29（5）：1017－1022.

钟小品，薛建儒，郑南宁，等.基于融合策略自适应的多线索跟踪方法［J］.电子与信息学报，2007，29（5）：1017－1022.

［7］ Wang Yongzhong，Liang Yan，Zhao Chunhui，et al.Kernal－based tracking based on adaptive fusion of multiple cues［J］.Acta Automatica Sinica，2008，34（4）：393－399.

王永忠，梁彦，赵春晖，等.基于多特征自适应融合的核跟踪方法［J］.自动化学报，2008，34（4）：393－399.

［8］ Li Peihua.An improved mean shift algorithm for object tracking［J］.Acta Automatica Sincia，2007，33（4）：347－354.

李培华.一种改进的Mean Shift跟踪算法［J］.自动化学报，2007，33（4）：347－354.

［9］ Yuan Guowu，Xu Dan.A moving objects tracking al－gorithm that combins texture and color［J］.Computer Applications and Software，2011，28（11）：81－84.

袁国武，徐丹.一种结合了纹理和颜色的运动目标跟踪算法［J］.计算机应用与软件，2011，28（11）：81－84.

［10］Birchfield S T，Rangarajan S.Spatiograms versus histograms for region－based tracking［C］.United States：IEEE，2005：1158－1163.

［11］Gu Xin，Wang Haitao，Wang Lingfeng，et al.Fusing multiple features for object tracking based on uncertainty measurement［J］.Acta Automatica Sinica，2011，37（5）：550－559.

顾鑫，王海涛，汪凌峰，等.基于不确定性度量的多特征融合跟踪［J］.自动化学报，2011，37（5）：550－559.

［12］Liu Qing，Tang Linbo，Zhao Baojun，et al.Infrared target tracking based on adaptive multiple features fusion and mean shift［J］.Journal of Electronics ＆Information Technology.2012，34（5）：1137－1141.

刘晴，唐林波，赵保军，等.基于自适应多特征融合的均值迁移红外目标跟踪［J］.电子与信息学报，2012，34（5）：1137－1141.

［13］Katja N，Esther K M，Luc V G.An adaptive colorbased filter［J］.Image Vision Computing，2003，21（1）：99－110.

［14］Yao Zhijun.A new spatiogram similarity measure method and its application to object tracking［J］.Journal of Electronics ＆ Information Technology，2013，35（7）：1644－1649.

姚志均.一种新的空间直方图相似性度量方法及其在目标跟踪中的应用［J］.电子与信息学报，2013，35（7）：1644－1649.

［15］Xu Kun，Yang Xiaojun，Guo Lanying.A multi－feature tracking algorithm based on spatial histogram［J］.Computer Engineering and Applications，2012，48（19）：28－31.

徐坤，杨小军，郭兰英.一种基于空间直方图的多特征目标跟踪算法［J］.计算机工程与应用，2012，48（19）：28－31.

［16］Zhang K.Real－time compressive tracking［C］.Berlin：Springer－Verlag，2012：864－877.

［17］Xu Wanjun，Hou Zhiqiang，Yu Wangsheng，et al.Fusing multi－feature for object tracking algorithm based on color and space［J］.Journal of Air Force ＆Engineering University，2015，16（6）：39－43.

许婉君，侯志强，余旺盛，等.基于背景加权的多特征融合目标跟踪算法［J］.空军工程大学学报，2015，16（6）：39－43.