一种采用干涉仪测量光电稳瞄系统稳定精度的方法研究

刘海波，王 晶，刘召庆，胥青青，侯利冰

引言

光电稳瞄系统装载于飞机、无人机、车辆、船舶等各类载体平台上，旨在为光电传感器提供稳定的观察平台，从而最大限度地发挥光电传感器的性能。观察平台的稳定程度可以用稳定精度来表示，即当光电稳瞄系统处于扰动环境下，系统内环残余的扰动角即为光电稳瞄系统的瞄准线稳定精度［1－3］。目前，在光电稳瞄系统领域中，稳瞄系统稳定精度的测量方法主要有2种：1）测量处于扰动条件工作的平台陀螺速度信号，通过对该信号进行积分、统计等数据处理来求取稳定精度指标；2）采用平行光管模拟无穷远目标，计算处于扰动中稳瞄系统图像上目标的偏差，得到稳定精度。这两种方法人为因素较多，误差量大，精度低［1－2］。随着应用市场对光电稳瞄系统精度要求的提高，传统测量方法已经逐步满足不了系统测试的精度需求［4－5］。泰曼格林干涉仪是一种较为精密的测量仪器，经常用于测量气体和固体的折射率。本文分析了泰曼格林干涉仪的测量原理，结合稳瞄系统的工作特点，提出了一种采用泰曼格林干涉仪测量光电稳瞄系统瞄准线稳定精度的方法，实验结果表明其测量分辨率较高，可测量粗精二级稳定系统的精度指标［6－7］。

1 干涉仪测量原理

如图1所示，泰曼格林干涉仪是迈克尔逊干涉仪的一种变型，在光学仪器制造工业中，常用这种仪器产生的等厚条纹对光学零件或光学系统作综合质量检验。它与原始的迈克尔逊干涉仪的不同点是，光源是单色点光源，它置于一个校正像差的透镜L1的前焦点上，而从干涉仪射出的光用另一个校正像差的透镜L2会聚，人眼（或CCD）则处在透镜L2的焦点位置观察（或接收）。由于泰曼格林干涉仪只使用单色光源，所以不需要迈克尔逊干涉仪中的补偿板［8－9］。

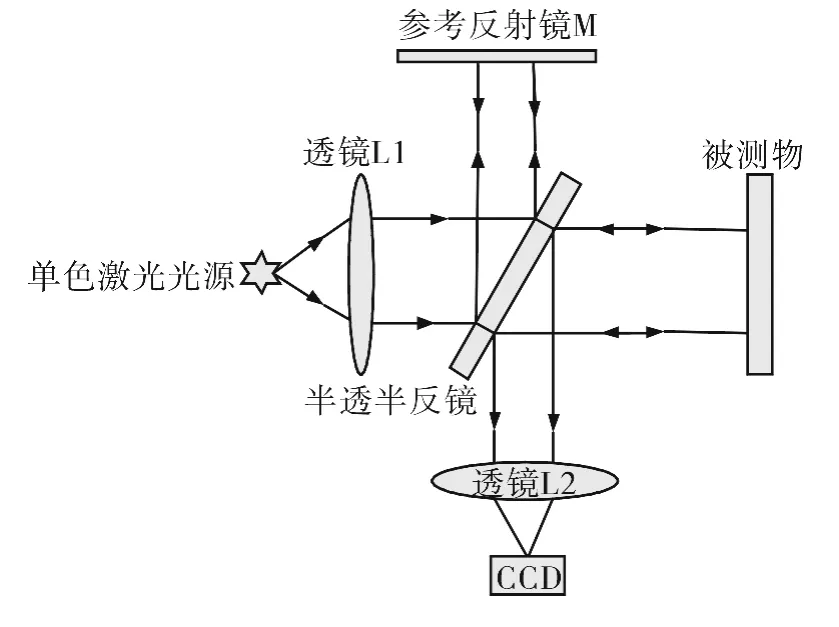
图1 泰曼干涉仪工作原理示意图Fig.1 Operation principle diagram of Twyman－Green interferometer

调节图1中参考反射镜M和被测物，使参考反射镜M与被测物严格正交，此时，成像CCD中形成一组干涉条纹。当被测物体发生角扰动或平动时，由于光程差发生改变，成像CCD中的干涉条纹将发生移动，条纹的移动量与光程差Δ的变化存在对应关系，亦即：

光程差Δ＝Nλ

式中：N表示干涉条纹的移动量；λ表示单色点光源的波长。

于是，通过监测成像CCD中干涉条纹的移动量，可以计算出被测反射镜产生的运动量。

2 基于干涉仪的稳定精度测量方法

根据泰曼格林干涉仪的工作原理以及光电稳瞄系统稳定精度的定义，提出采用泰曼格林干涉仪测量光电系统稳定精度的方法，其测量原理如图2所示。

图2 利用泰曼干涉仪测量稳瞄系统稳定精度原理示意图Fig.2 Principle diagram for measuring stabilization precision of stabilized aiming system utilizing Twyman－Green interferometer

2.1 测试系统构成与功能

稳定精度测量系统由4个主要构成单元：泰曼格林干涉仪、信息处理计算机、待测光电稳定系统和振动平台。图2中，左侧虚线表示泰曼格林干涉仪系统，其输出进入计算机进行信息处理；右侧的光电稳定系统为被测物，放置于振动平台上。

在光电稳瞄系统的待测部件上安装一平面反射镜，安装时通过光学校正装置保证其法线与干涉仪平行光平行。为减少平动对干涉波的影响，一般可考虑将泰曼格林干涉仪放置在离被测系统2m以上的地方。

当光电稳瞄系统工作在振动环境下时，导致光电系统的动不平衡［10］，使得稳瞄系统相对干涉仪存在角运动和平动。这些运动信息通过干涉仪形成干涉波的运动，计算机通过干涉波运动的分析计算角运动信息，以此获取系统稳定精度。

2.2 测试系统测量原理

当被测反射镜由最初的垂直于参考反射镜M发生微小的角运动和平动后，到达一个新的位置时，如图2所示。一般考虑｜AB｜远大于r，则忽略平动r对测量结果的影响。设被测稳瞄系统焦距为f，反射镜长度为m，被测反射镜偏转角度θ，干涉仪将产生光程差：

由于光电稳瞄系统在振动环境下系统内环的微小振动量θ很小，因此可近似地将干涉仪的光程差表示为

当干涉仪存在光程差时，干涉仪的干涉条纹将发生移动。根据干涉仪的工作原理有：

式中：N为移动的干涉条纹数；λ为所应用光源的波长。

根据干涉条纹的移动量得到系统角运动与平动引起的被测平面镜的移动量为H＝θm＝Nλ／2，则被测系统稳定精度为w＝H／f。

2.3 测量图形结果分析

图3是采用泰曼格林干涉仪测量稳瞄系统内环俯仰方向稳定精度的干涉图结果。实验采用的光源是波长为638.2nm 的单色激光［7－8］，图像采集CCD的分辨率为600像素×800像素，单帧图像的频率为25Hz。采用Matlab软件编写程序，计算干涉图像的干涉结果。

图3 泰曼格林干涉仪测试图Fig.3 Twyman－Green interference patterns

由程序计算可知，在图3（a）、3（b）、3（c）、3（d）这4幅图中，条纹依次移动半条，即ΔN＝，于是，反射镜的变化量λ＝0.16μm。

当干涉图中的条纹移动量不是半条纹的整数倍时，计算机程序会计算条纹在成像CCD上移动的像素数，从而计算出反射镜的偏移量。

3 实验测试与数据分析

构建两项实验进行验证，其测试系统分别如图4和5所示。图4中试验对象为FSM，FSM反射镜的尺寸φ为25mm，精度为0.2μrad，带宽为380Hz；图5中试验对象为某型光电稳瞄产品，试验装置采用波长为632.8nm的单色激光光源和ZYGO干涉仪。

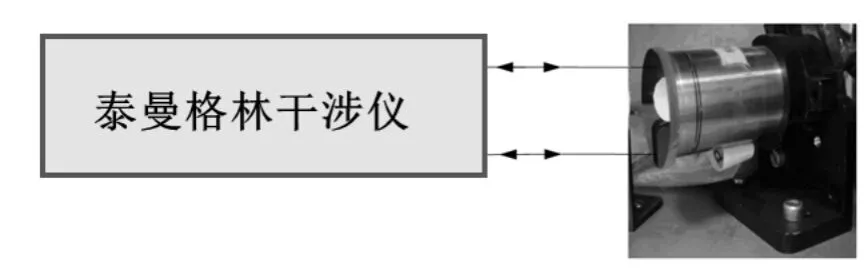
图4 系统验证实验原理图Fig.4 Verified experiment principle diagram

3.1 快速反射镜指向精度测试

图4 中FSM接收计算机方波指令，幅值为1μrad，频率为1.0Hz，干涉仪装置中图像采集系统的采样频率为1kHz，采样时间为5s。通过监控干涉仪回馈的角度信息，得到测试结果如图6和图7所示。

图5 系统验证试验实物图Fig.5 Verified experiment physical graph

图6 方位测试结果Fig.6 Azimuth test result

图7 俯仰测试结果Fig.7 Pitch test result

由图6可知，方位轴的运动中心位置在－0.5 μrad处，由图7可知，俯仰轴的运动中心位置在0.4μrad处，因此两轴的测量结果中心均不为0。同时可看到噪声对应的运动约为0.2μrad，这意味着该FSM最小可分辨运动角度应不小于0.2μrad。

3.2 光电系统稳定精度测试

按照原理图2，将某型光电稳定系统置于振动平台上进行稳定精度测试。计算机采样频率为6 125Hz，采样时间为2.6s，得到测试数据如图8（a）所示。

对所采集的数据进行频谱分析得到图8（b）结果，可以看出角运动频率主要集中在0～60Hz的低频段和300Hz～400Hz的中频段。

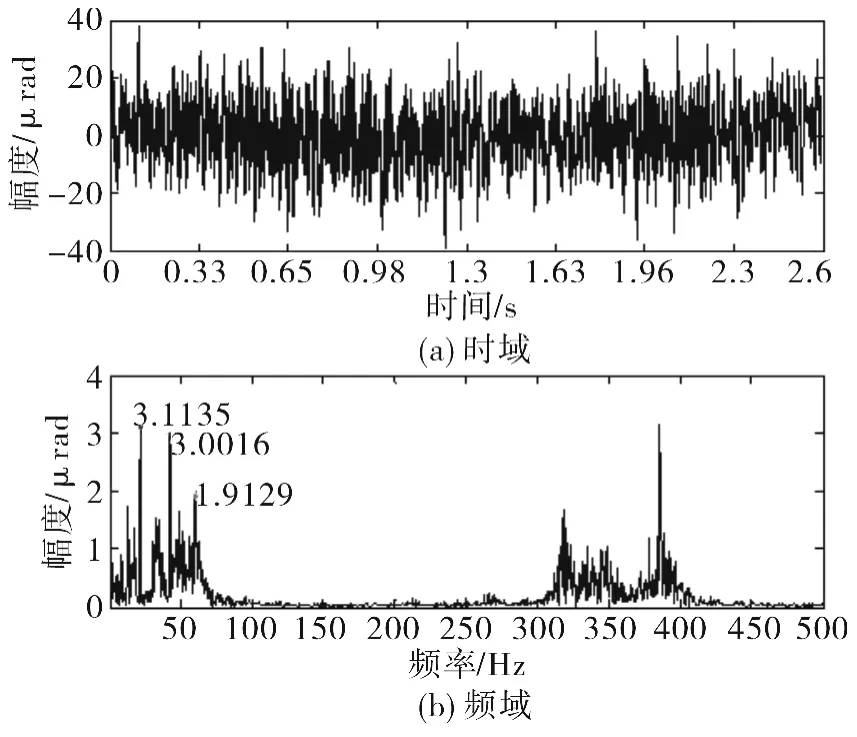
图8 某型稳瞄系统稳定精度分析图Fig.8 Stabilization accuracy of stabilized sighting system

对采集数据进行分析计算得到稳定精度：

式中：η代表系统稳定精度；n代表采集的数据数量；Ai代表采集的第i个数据，i为整数；¯A代表采集数据的平均值。

经计算得到该被测稳瞄系统的稳定精度达10μrad。这一结果与产品定型测试结果高度一致，验证了该测量方法的有效性。

5 结论

在分析泰曼格林干涉仪工作原理的基础上，提出了基于干涉仪的稳定精度测量方法，通过对FSM和光电稳瞄产品的实验测量，验证了测试系统对稳定精度的测量精度达0.2μrad，并可实现稳定精度为10μrad的稳瞄产品的测试。

［1］ Xu Feifei，Ji Ming，Xie Jing，et al.Application of FSM in high accuracy line－of－sight stabilizartion system［J］.Journal of Applied Optics，2012，33（1）：10－13.

徐飞飞，纪明，解静，等.FSM在高精度瞄准线稳定系统中的应用研究［J］.应用光学，2010，31（1）：19－22.

［2］ Xiang Shiming，Gao Jiaobo，Ji Ming，et al.Modern optic electro image technique［M］.Beijing：Beijing Institute of Technology Press，2010，128－193.

向世明，高教波，焦明印，等.现代光电子成像技术概论［M］.北京：北京理工大学出版社，2010.

［3］ Ji Ming，Xu Peizhong，Xu Feifei.Development of optoelectroic system sforarmed［J］.Journal of Applied Optics，2010，31（1）：19－22.

纪明，许培忠，徐飞飞.武装直升机光电系统发展与对策［J］.应用光学，2010，31（1）：19－22.

［4］ Ji Ming.Simulation and error analysis of the reflect mirror stabilization system［J］.Journal of Applied Optics，2000，21（5）：19－22.

纪明.反射镜稳定系统的仿真与误差分析［J］.应用光学，2000，21（5）：19－22.

［5］ Zhang Jingyue，JI Ming，Wang Huilin.Modeling and simulation of airborne stabilized sighting system［J］.Journal of Applied Optics，2006，27（6）：491－496.

张璟玥，纪明，王惠林.机载稳瞄控制系统模型及仿真分析［J］.应用光学，2006，27（6）：491－496.

［6］ Fu Rongguo，Chang Benkang，Qian Yunsheng，et al.Optical axis collimation of the laser designation［J］.Optical Technique，2007，33（2）：41－43.

富容国，常本康，钱芸生，等.激光指示器光轴调校技术［J］.光学技术，2007，33（2）：41－43.

［7］ Masten M，Hilkert J M.Electromechanical system configuration for pointing，tracking，and stabilization applications［J］.SPIE，1987，779：75－87.

［8］ Masten M.Inertially stabilized platforms for imaging optical systems［J］.IEEE CSM，2008，28：47－64.

［9］ Zhou Liwei，Liu Yuyan.Target detection and identify［M］.Beijing：Beijing Institute of Technology Press，2002.

周立伟，刘玉岩.目标探测与识别［M］.北京：北京理工大学出版社，2002.

［10］Han Jun，Wang Jing，Chen Wenjian，et al.The study of the adjustment of the rotate multi－spectral multioptical axis［J］.Laser ＆ Infrared，2009，39（4）：415－416.

韩军，王晶，陈文建，等.空间旋转多光谱多光轴校准技术研究［J］.激光与红外，2009，39（4）：415－416.