利用低轨卫星激光资料检验地球引力场模型的精度∗

汪宏波 赵长印 张 伟 旃进伟 喻圣贤

(1中国科学院紫金山天文台南京210008)

(2中国科学院空间目标与碎片观测重点实验室南京210008)

(3宇航动力学国家重点实验室西安710043)

利用低轨卫星激光资料检验地球引力场模型的精度∗

汪宏波1,2,3†赵长印1,2张 伟1,2旃进伟1,2喻圣贤1,2

(1中国科学院紫金山天文台南京210008)

(2中国科学院空间目标与碎片观测重点实验室南京210008)

(3宇航动力学国家重点实验室西安710043)

地球引力场模型是人造卫星轨道计算中最重要的动力学模型之一.近年来国际上空间重力卫星计划取得了极大成功,相继推出了一系列新的引力场模型.从近地卫星轨道计算的角度检验了2种传统引力场模型(JGM3,EGM96)和4种新引力场模型(EIGENCHAMP05S,GGM03S,GOCE02S,EGM2008)的精度,利用4颗近地卫星的激光测距资料进行精密定轨预报,统计比较了不同模型的定轨残差和预报误差.结果表明:(1)4种新引力场模型精度基本在同一水平,对于近地卫星定轨精度普遍优于9 cm,最高达到5 cm,相对于JGM3和EGM96模型有明显改善;(2)以JGM3模型为基准,EGM96模型的精度有所提高,2000年以后的4种新模型的精度则普遍提高了12%∼47%(定轨)和63%(预报). 70阶之前定轨精度随着模型阶次增大而提高,70阶以后定轨精度基本保持稳定,这表明对于近地卫星轨道计算而言,70阶的引力场已经能够满足厘米级的精度需求.

天体力学,方法：数值,引力,轨道计算和定轨

1 引言

在人造卫星动力学中,地球对卫星的引力作用可以分为中心引力和非球形摄动力两个部分,其中非球形摄动力主要是由于地球形状不规则、质量分布不均匀引起的.人们常用地球引力场模型来描述这种不规则、不均匀的引力场.几十年来,随着测量手段的日益丰富,测地精度的不断提高,新的引力场模型陆续推出.尤其是在21世纪之后,CHAMP(CHAllenging Mini-satellite Payload)[1]、GRACE(Gravity Recovery and Climate Experiment)[2]和GOCE(Gravity field and steady-state Ocean Circulation Explorer)1http://www.esa.int/Our_Activities/Observing_the_Earth/GOCE等空间重力计划相继实施.以2001年CHAMP卫星发射为标志,在这之前被称为Pre-CHAMP时期,这个时期的引力场模型主要依赖地面对空间卫星的测量资料(SLR、DORIS以及少量GPS数据等),资料精度和分辨率有限;而在CHAMP计划之后,重力卫星普遍搭载了GPS接收机、星载加速仪、星间微波测距仪(用于GRACE)、重力梯度仪(用于GOCE)等设备,极大提高了引力场反演的精度和时空分辨率.

本文将研究以下6种地球引力场模型:JGM3、EGM96、EIGEN-CHAMP05S、GGM03S、GOCE02S、EGM2008.主要内容是采用低轨卫星的激光资料进行精密定轨,检验不同引力场模型的精度,为近地卫星精密定轨和预报选择合适的引力场模型提供依据.在测地学中,评估引力场模型精度有很多种途径,例如利用GPS水准点等独立资料评估模型的大地水准面精度[3]、重力异常等.而本文将从低轨卫星轨道摄动的角度评价模型精度,因为通过对特定目标跟踪数据的精密定轨和预报也是检验引力场模型精度的手段之一[4].

第2节将介绍6种引力场模型以及用于试验的4颗卫星的资料概况;第3节以CHAMP、GFZ-1和SWARM-A卫星的激光测距资料(SLR)为观测量,分别使用6种引力场模型进行精密定轨,检验这些模型在定轨中的精度水平,并利用GRACE-A卫星资料分析引力场模型精度在预报阶段有何种差异.最后将给出结论和讨论.

2 模型与方法

2.1 引力场模型及其数学形式

一般地,地球非球形摄动∆V可以用球谐函数表示为

其中,GMe是地球的地心引力常数;l,m分别为引力场的阶次;ae是地球参考椭球体的赤道半径;lm是缔合勒让德多项式.R,φ,λG分别为空间中某一点在地固坐标系下的地心距、纬度和经度.是归一化后的球谐系数;以上参数中都是由具体的引力场模型所给出.

长期以来,人们利用地面重力资料和卫星轨道资料测定引力场系数和提出了几十种地球引力场模型,模型阶次和精度不断提高.本文选择在上世纪90年代中后期发表的两个模型JGM3和EGM96作为研究对象,它们是在Pre-CHAMP时期最具代表性的两个引力场模型.

JGM3模型[4],全称为Joint Gravity Model 3,由1996年德克萨斯大学奥斯汀分校的空间科学研究中心(CSR)发布,最高阶次为70×70,是各种定轨预报系统中应用较多的高精度地球引力场模型.它在JGM1模型的基础上融合了LAGEOS 1、LAGEOS 2和Stella卫星的SLR数据,SPOT 2卫星的多普勒数据(DORIS)以及TOPEX/ POSEIDON的GPS数据等.

EGM96模型2http://cddis.nasa.gov/egm96/egm96.html,全称为Earth Gravitational Model 1996,由美国NASA哥达德飞行中心、美国测绘局、俄亥俄州立大学联合发布,使用了TOPEX/POSEIDON、ERS1和GEOSAT卫星的测高资料、地面重力异常资料,以及30余颗卫星跟踪数据(GPS,SLR, DORIS等类型).相比于JGM3模型,EGM96使用的卫星资料更多,同时增加了在中国、前苏联、南美和非洲等地的地面重力资料.360阶的EGM96模型在一段时期内则被认为是精度最高的模型.值得指出的是,在GPS全球定位系统中广泛使用的WGS84坐标系统(G873),也吸纳了EGM96模型作为其标准的引力场模型,并用于建立大地水准面,从1996年10月1日起生效[5].

2.2 重力卫星计划与引力场模型

进入21世纪以来,随着GPS技术、三轴加速度仪、星间跟踪、重力梯度仪等高精度传感技术被用于空间的重力测量,一批重力卫星计划相继实施.2000年德国的CHAMP卫星发射成功;2002年德国、美国联合实施的GRACE计划发射了两颗GRACE卫星(A/B).这两个计划首次实现了空间重力测量的几个科学要素[6]:(1)采用低轨运行方案,近距离传感地球引力场对卫星运行的扰动;(2)采用了近圆极轨道覆盖地球表面;(3)用星载三轴加速度计精确测定非保守力;(4)搭载GPS接收机实现实时精密定轨.这些特点使得只用一颗卫星的资料就能精确测定引力场,而在Pre-CHAMP时期,则需要联合多颗卫星长期的精密轨道解算引力场.

在CHAMP计划取得成功后,相继开展的GRACE和GOCE计划进一步增加了新的测量技术.例如GRACE增加了两颗星之间的星间微波测距(“低-低”星间跟踪),这种新的观测量提高了引力场模型的时空分辨率,几个月的资料就能得到一个完整引力场,使得研究引力场随时间的变化成为现实,在海平面变化、地下水监测、重大地质活动预报等方面发挥了重要作用.2009年发射的GOCE卫星则首次使用了重力梯度仪,直接测量引力场的2阶导数,这是人类第1次不再是单纯采用从卫星轨道摄动来达到从空间求定引力场的目标[7],而且使用了无拖曳加速仪,使得卫星能在极低的高度(250 km)克服大气阻力进行引力场测量,为求解引力场高阶系数提供了条件.

利用这些重力卫星的数据,国际上不同的机构或学者纷纷发表了各自的引力场模型,比较著名的有EIGEN系列、GGM系列、EGM系列,下面将选择它们的最新版本作简单介绍,同时兼顾不同资料来源和不同系列,力求全面.

EIGEN-CHAMP05S模型[8](以下简称CHAMP05S):该模型是德国地球科学研究中心(GFZ)使用CHAMP卫星在整个任务期间(2002—2008)共6 yr的星间跟踪(Satellite-Satellite Tracking,SST)数据、三轴加速仪数据求解而成,最大阶次为150阶.

GGM03S模型[7]:该模型是CSR使用GRACE卫星2003—2006年共47个月的GRACE资料求解得到(2004年1月资料缺失),最高阶次为180阶.

GOCE02S模型[9]:该模型采用了2009—2012年的GOCE重力梯度仪、加速仪、星间跟踪等数据求解,最高阶次为230阶.

EGM2008模型[10]:该模型采用2002年9月至2007年4月的57个月GRACE资料星间跟踪资料,构建了前180阶的模型系数.然后通过高精度、高分辨率的地面资料,首次将模型的阶数提高到2190阶,是迄今为止阶数最高的模型,是引力场模型构建的一个里程碑.

2.3 用于研究的低轨卫星资料

从国际激光测距服务网(International Laser Ranging Service)上可以查阅有激光测距资料的卫星,我们挑选了4颗近地卫星(CHAMP,GFZ-1,GRACE-A,SWARM-A)作为研究对象,并下载其激光测距资料.卫星的具体信息见表1(按轨道高度排序).

之所以选择近地卫星作为研究对象,主要是因为引力场的信号会随着高度增加而衰减,只有低轨卫星的轨道才能对引力场系数有较显著的响应,而高轨道卫星往往只对20阶以下的引力场有响应.同时,考虑到引力场摄动量级较小,需要厘米级的精密轨道才能分辨和检验引力场模型的精度,因此选择近地卫星的激光测距资料作为研究的基础.

挑选近地卫星的标准主要有:轨道倾角较大,轨道高度较低,时间跨度较长且资料连续.以上4颗近地卫星比较有代表性.从轨道倾角上看,CHAMP、GRACEA和SWARM-A这3颗卫星的倾角都接近90◦,属于极轨道卫星,GFZ-1的倾角也达到52◦,因此它们的轨道分布对全球引力场都有较好的反映.从高度上看,CHAMP卫星在寿命末期轨道高度低于300 km,GFZ-1卫星的高度约370 km,GRACE-A和SWARMA卫星高度均为460 km,可对不同高度的卫星开展SLR数据精密定轨试验.特别是对于GRACE-A卫星不仅可以用SLR数据定轨,还可以进行24 h的轨道预报,再调用GFZ发布的GRACE卫星事后轨道(Rapid Science Orbit,RSO)对预报结果进行外部标定(RSO轨道的精度约为20 cm).

同时,我们还注重合理地选择资料时间.CHAMP、GRACE-A和SWARM-A卫星资料时间集中在2009—2014年,而GFZ-1卫星的资料时间为1997年,时间间隔长达12 yr以上.用不同时期的资料检验模型精度,兼顾了测试条件的平等性,保证了测试结果的代表性.

当然,在低轨卫星的定轨预报中不可避免地会存在大气阻力摄动的影响.为此我们只选择太阳和地磁活动平静时期的资料,因为空间环境有扰动时,大气模型误差将掩盖地球引力场模型之间的差异.不仅如此,我们在定轨中还特别求解沿迹方向的经验加速度,尽量减少大气模型误差对定轨的影响.同时,这4颗卫星的形状、质量参数是已知的,姿态保持稳定,有利于大气阻力和太阳光压摄动的计算.需要指出的是,采用运动学定轨的方法能够完全避开大气模型的误差,从而实现高精度的定位[11−12],但是它同时也避开了引力场模型,不能为引力场模型分析提供有用信息,因此本文仍采用动力学定轨法.

为了证明试验有效,需要保证研究资料的独立性.例如,虽然CHAMP，GRACEA卫星本身就是重力卫星,但所选的资料时间段均在2009年以后,晚于资料建模时刻.换言之,这些测试资料都没有被用于建模,对于待检验的6个模型而言这些SLR资料是独立的.

表1 用于研究的4颗低轨卫星的信息Table 1 Information of 4 LEO satellites for this study

2.4 分析方法

对于CHAMP、GFZ-1和SWARM-A卫星,主要方法是利用SLR资料定轨,统计定轨后的资料残差作为定轨精度的指标.定轨弧长为1 d,求解参数有:卫星的位置速度矢量大气阻力系数CD、太阳光压系数CR以及沿迹方向的经验加速度.这些定轨参数的组合可以较好地刻画大气阻力摄动和太阳光压摄动,从而分离出地球引力场摄动对轨道的影响.

对于GRACE-A卫星,则增加了轨道预报环节,即先采用1 d的SLR资料进行定轨,求解预报初值和阻力系数CD、光压系数CR,再向后预报1 d.需要说明的是,在预报之前的定轨环节不再求解经验加速度,因为经验加速度参数往往只对定轨有贡献,能提高内符合精度,但不适用于轨道预报,因为它不具备清晰的物理意义,也不代表真实的力学机制.对于4颗卫星,我们采用相同的动力学模型和参数系统(表2).

在结果分析中,一方面采用纵向比较,对于同一模型截断至不同的阶次,观察模型精度随阶次的变化规律;另一方面进行横向比较,在相同阶次条件下观察不同模型的精度.

表2 定轨和预报所采用的动力学模型与参数系统Table 2 Models and parameters used in the orbit determination and prediction

3 结果分析

3.1 CHAMP卫星的精密定轨

本节分别采用不同的地球引力场模型,对CHAMP卫星的SLR资料进行精密定轨,统计定轨后的资料残差.需要说明的是由于CHAMP卫星轨道高度很低,1 d内激光站的测量普遍偏少,当只有单站测距资料时无法实现定轨[13−14].而且我们只挑选日平均地磁指数小于15的资料(为了避免地磁扰动对定轨的影响).在这些限定条件下, 2010年3∼9月中只有61 d的资料满足1 d弧长定轨的要求.

为了观察不同引力场阶次对模型精度的影响,我们对每个模型从20阶至120阶,按照5阶步长递增,观察截断至不同阶次时的定轨精度.

图1的横坐标为引力场模型截断阶次,纵坐标为定轨后的资料残差,单位是cm.为了清晰展示结果,图中只给出了JGM3、EGM96和EGM2008模型的曲线.总体而言,在3个模型中EGM2008模型的定轨残差最小,尤其是在40阶以后表现明显,意味着该模型精度最高.以70阶为例,JGM3模型定轨的资料残差为12 cm,EGM96模型为7.6 cm,EGM2008模型为6 cm.从图中还可以看出引力场的精度随截断阶次的变化趋势,以EGM2008模型为例,引力场阶次取20阶时定轨精度27 cm,取40阶时定轨精度约8 cm,取70阶时定轨精度6 cm,精度整体呈现提高的趋势;当阶次进一步提高时定轨精度有细微波动,但总体维持在6 cm的水平,阶次的提升对定轨精度没有实质影响.因此,对于近地卫星的轨道计算,引力场模型截断至70阶就能够满足厘米级的精度需求.

图1 模型取不同截断阶次时的定轨残差Fig.1 The residual error of observation in orbit determination vs.the model’s truncation degree

全部模型的定轨精度见表3(单位为cm),对于每个模型分别截断至40阶、70阶、100阶、150阶和180阶.结果显示4种新模型的精度在同一水平,相同阶次的残差统计结果的差别仅在毫米级,精度显著优于JGM3和EGM96.如果以70阶的JGM3模型精度(12 cm)为基准,EGM96模型精度提高了37%,而后4种模型精度普遍提高了47%.

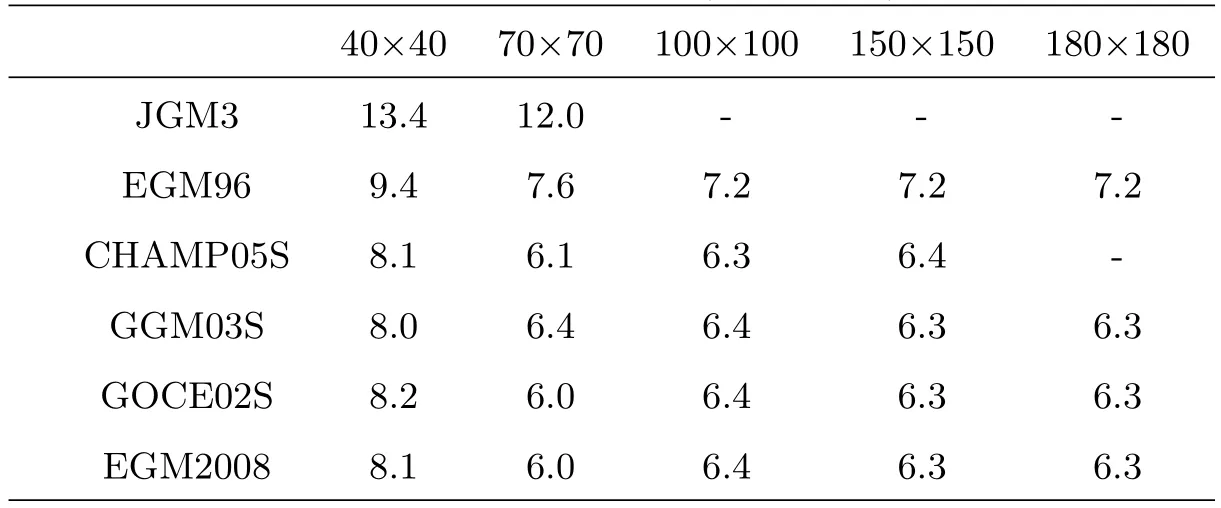
表3 6种模型取不同阶次时的定轨精度比较(CHAMP)Table 3 Comparison of orbit determination accuracy of 6 models with di ff erent truncation degrees(CHAMP)

3.2 GFZ-1卫星的精密定轨

本节采用GFZ-1卫星的SLR资料定轨,卫星高度约370 km,与上一节CHAMP卫星的高度接近.选取的GFZ-1的资料时间段为1997年,比CHAMP卫星资料提前了12年.采用不同时间段的资料评估将有助于得到更普适的结论.表4中给出了利用不同引力场模型的定轨结果,并考虑不同的截断阶次对定轨精度的影响.当模型阶次取70阶时, JGM3和EGM96模型的定轨残差均为9.9 cm,而后4种模型的残差为7∼8 cm,精度提高约1∼2 cm,相对值提高了12%∼24%.精度改善的幅度略低于CHAMP卫星的统计结果.原因在于GFZ-1的资料时间段(1997年)与后期的4种新模型的时间间隔略长,引力场随时间的变化较大,制约了精度的提升幅度.但总体来看后4种新模型精度仍然得到了提升.

表4 6种模型取不同阶次时的定轨精度比较(GFZ-1)Table 4 Comparison of orbit determination accuracy of 6 models with di ff erent truncation degrees(GFZ-1)

3.3 SWARM-A卫星的精密定轨

本节将采用SWARM-A卫星开展相同的试验.SWARM-A高度约为460 km,比CHAMP卫星高180 km,高层大气密度对定轨的影响有较大程度的降低,有利于凸显地球引力场的摄动影响.对于每个模型分别截断至40阶、70阶、100阶、150阶和180阶,统计定轨残差.具体结果见表5.总体来看JGM3模型精度较差,EGM96略好,精度最好的是后4种新模型.以70阶的JGM3模型为基准,EGM96模型精度提高了36%,其他4种模型精度提高了43%,这一结果与CHAMP卫星的试验结果是吻合的.

表5 6种模型取不同阶次时的定轨精度比较(SWARM-A)Table 5 Comparison of orbit determination accuracy of 6 models with di ff erent truncation degrees(SWARM-A)

3.4 GRACE-A卫星的精密预报

针对GRACE-A卫星,我们选择2010年8月至2011年1月的资料(跨度6个月),因为这一阶段太阳辐射流量F10.7的总体水平介于70∼90 sfu之间,日地磁指数Ap总体在15以下(仅有12天例外,已排除),见图2.这种空间环境下大气总密度变化平稳,经验大气模型误差对轨道预报的影响比较小.首先我们给出2010年11月1日的个例,即先用1 d的激光资料定轨,然后预报24小时(11月2日),最后利用RSO轨道作为独立外部检验,给出不同引力场模型的预报精度(见图3-4).之所以选择11月1日定轨,是因为这一天激光资料充足,共有5个站177组测距数据,有利于轨道确定和动力学参数的求解;而且这两天太阳和地磁活动非常平静,辐射指数F10.7仅为78 sfu,日地磁指数Ap为3,高层大气密度稳定.

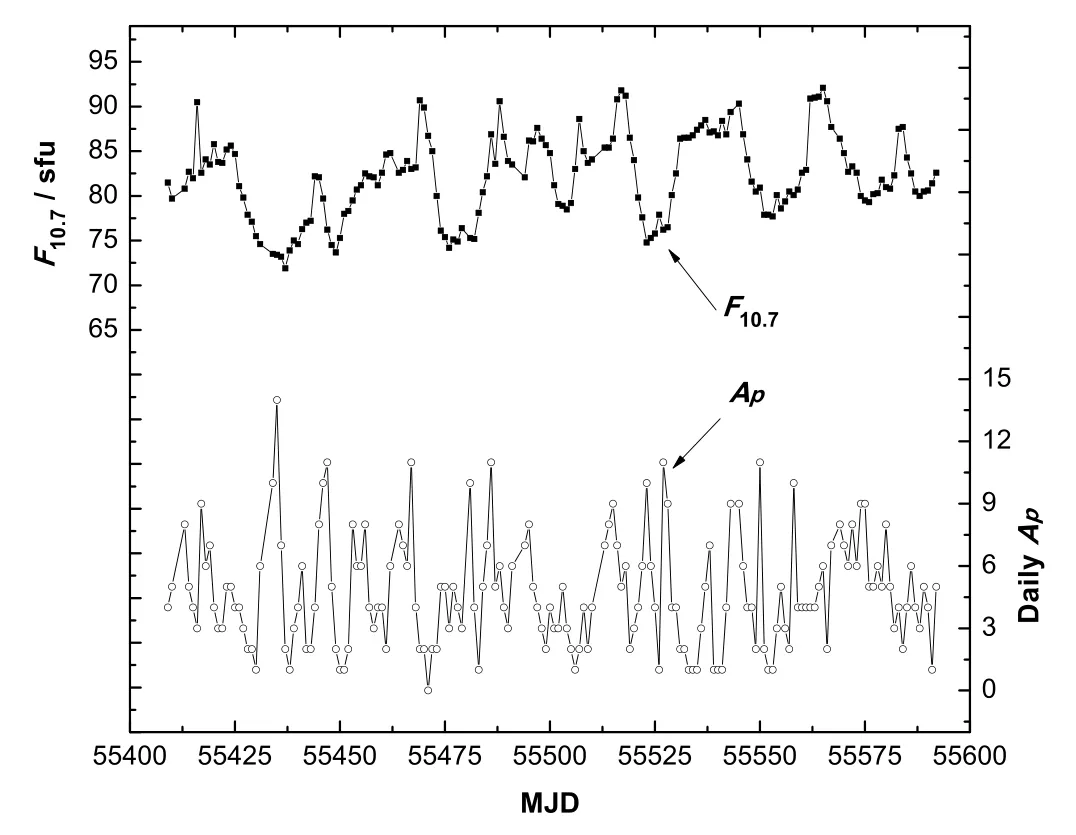
图2 太阳辐射指数和日地磁指数的变化(2010-08—2011-01)Fig.2 The changes of solar radiation index and daily geomagnetic index(2010-08—2011-01)

图3是JGM3、EGM96和EGM2008这3个模型的比较.可以看出:3个模型预报1 d的最大误差分别为260 m,126 m和93 m,JGM3精度最低,EGM96略优,EGM2008精度最高.如果以JGM3为参照,那么EGM2008精度提高了64%.图4给出了其他3个模型(CHAMP05S,GGM03S,GOCE02S)的预报误差曲线,3个模型误差曲线非常接近,最大误差分别为93 m,84 m和87 m,差别不是很明显.综合来看,后4种新模型的预报精度在同一水平(90 m左右),显著优于JGM3和EMG96(100∼300 m).

以上仅仅是个例,表6中则给出了全部88组有效资料的统计结果.之所以半年来只有88组资料是有效的,是因为能满足1 d资料定轨要求的情况很少(或者资料非常稀疏导致定轨失败).表6中第2列是1 d资料定轨的残差,第3、4、5列分别是预报24 h在径向、切向和法向的误差分量,单位是米.

图3 采用不同引力场模型预报精度的比较IFig.3 The comparison of orbit prediction accuracy with di ff erent gravitational field models(I)

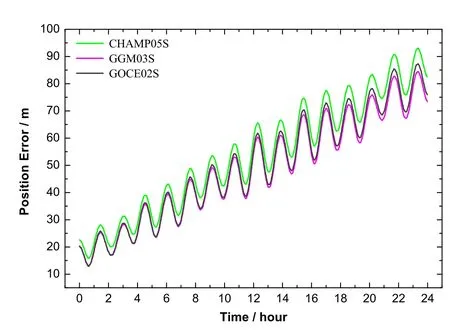
图4 采用不同引力场模型预报精度的比较IIFig.4 The comparison of orbit prediction accuracy with di ff erent gravitational field models(II)

从表6中的定轨残差上看,前2种早期模型精度约8∼9 cm,而后4种新模型精度为5 cm,表明新模型的定轨精度普遍提高约40%,这与上一节中SWARM-A的定轨结果是一致的(两颗卫星在同一高度范围).从预报精度上看,采用后4种新模型时径向精度从原模型的3∼5 m提高到2 m,在沿迹和法向方向也有20 m和1 m以上的精度提升.由于引力场是作用在径向的,我们选用径向精度描述引力场模型的预报精度,这也是国际上的通行做法.如果用JGM3作基准,后4种新模型在预报阶段精度提高约63%,精度提升是显著的.

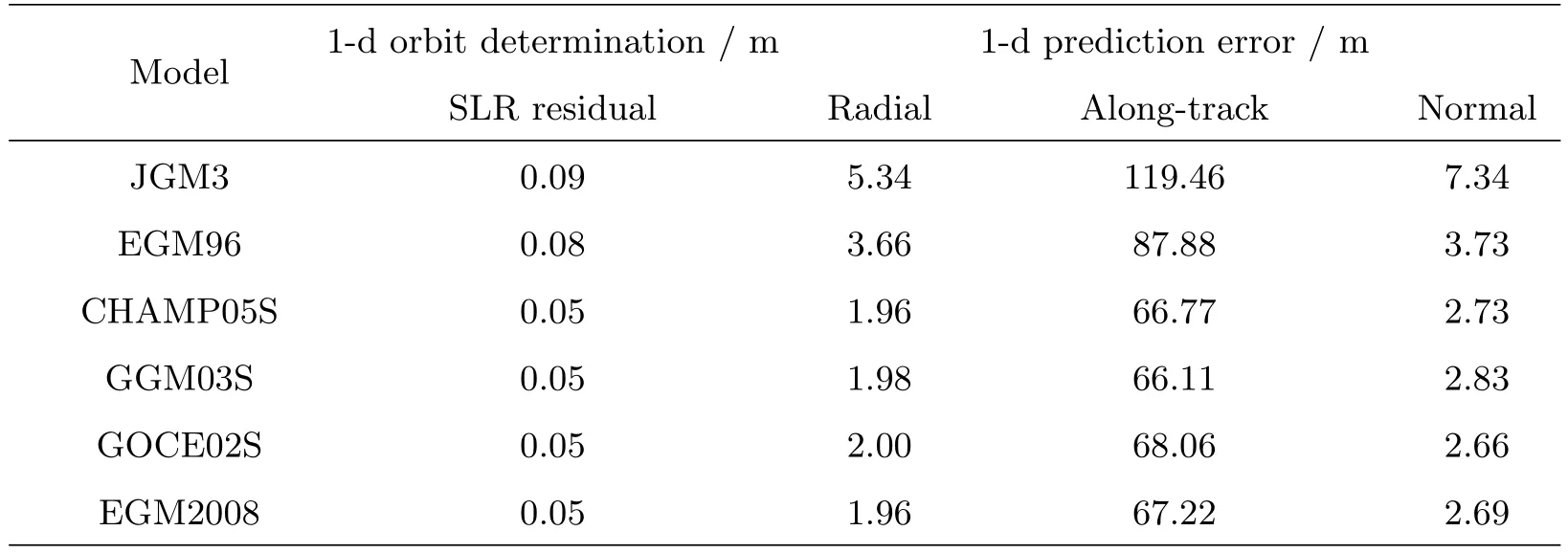
表6 采用6种模型的定轨和预报精度(GRACE-A,70×70)Table 6 The accuracies of orbit determination and prediction with 6 gravitationalfiled models(GRACE-A,70×70)

4 结论

本文从近地卫星轨道计算的角度检验了6种地球引力场模型的精度.通过采用4颗近地卫星的激光测距资料进行精密定轨和预报,统计比较了不同模型的定轨残差和预报误差.结果表明:(1)4种新引力场模型精度基本在同一水平,从4颗用于测试的低轨卫星统计情况看,定轨精度普遍优于9 cm,最高达到5 cm,相对于JGM3和EGM96模型有明显改善;(2)以JGM3模型为基准,EGM96模型略优,精度最高提升了37%,2000年以后的4种新模型的精度提高约12%∼47%(定轨)和63%(预报).此外还发现,在70阶之前定轨精度随着模型阶次增大而提高,大多数情况下70阶以后定轨精度基本保持稳定,但这并不意味着70阶以后的引力场精度没有提高,而是因为近地卫星激光资料对70阶引力场的响应已是极限,需要更精细的测量手段和资料才能对更高阶引力场的精度进行评判.

[1]Reigber C,L¨uhr H,Schwintzer P.AdSpR,2002,30:129

[2]Tapley B D,Bettadpur S,Watkins M M,et al.GeoRL,2004,31:L09607

[3]陈秋杰,沈云中,张兴福.地球物理学报,2013,56:2238

[4]Tapley B D,Watkins M M,Ries J C.JGR,1996,101:28029

[5]NIMA TR8350.2.Department of Defense World Geodetic System 1984,Its Definition and Relationships with Local Geodetic Systems.Third Edition Amendment 1.National Imagery and Mapping Agency,2000:xiii

[6]陈俊勇.地球科学进展,2006,21:661

[7]Tapley B,Ries J,Bettadpur S,et al.AGU Fall Meet.Suppl.,2007,88:Abstract G42A-03

[8]Flechtner F,Dahle C,Neumayer K H,et al.System Earth via Geodetic-Geophysical Space Techniques Advanced Technologies in Earth Sciences.Berlin:Springer,2010:41-58

[9]Yi W.AdSpR,2012,50:371

[10]Pavlis N K,Holmes S A,Kenyon S C,et al.JGR,2012,117:B04406

[11]彭冬菊,吴斌.天文学报,2011,52:495

[12]Peng D J,Wu B.ChA&A,2012,36:291

[13]梁智鹏,刘承志,范存波,等.天文学报,2012,53:137

[14]Liang Z P,Liu C Z,Fan C B,et al.ChA&A,2012,36:471

Evaluation of Gravitational Field Models Based on the Laser Range Observation of Low Earth Orbit Satellites

WANG Hong-bo1,2,3ZHAO Chang-yin1,2ZHANG Wei1,2ZHAN Jin-wei1,2YU Sheng-xian1,2
(1 Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008)
(2 Key Laboratory of Space Object and Debris Observation,Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210008)
(3 State Key Laboratory of Astronautic Dynamics,Xi’an 710043)

The Earth gravitational filed model is a kind of important dynamic model in satellite orbit computation.In recent years,several space gravity missions have obtained great success,prompting a lot of gravitational filed models to be published.In this paper,2 classical models(JGM3,EGM96)and 4 latest models,including EIGENCHAMP05S,GGM03S,GOCE02S,and EGM2008 are evaluated by being employed in the precision orbit determination(POD)and prediction,based on the laser range observation of four low earth orbit(LEO)satellites,including CHAMP,GFZ-1,GRACEA,and SWARM-A.The residual error of observation in POD is adopted to describe the accuracy of six gravitational field models.We show the main results as follows: (1)for LEO POD,the accuracies of 4 latest models(EIGEN-CHAMP05S,GGM03S, GOCE02S,and EGM2008)are at the same level,and better than those of 2 classical models(JGM3,EGM96);(2)If taking JGM3 as reference,EGM96 model’s accuracy is better in most situations,and the accuracies of the 4 latest models are improved by 12%-47%in POD and 63%in prediction,respectively.We also confirm that the model’s accuracy in POD is enhanced with the increasing degree and order if they are smaller than 70,and when they exceed 70 the accuracy keeps stable,and is unrelated with the increasing degree,meaning that the model’s degree and order truncated to 70 are sufficient to meet the requirement of LEO orbit computation with centimeter level precision.

celestial mechanics,methods:numerical,gravitation,orbit calculation and determination

P135;

A

10.15940/j.cnki.0001-5245.2015.05.006

2014-12-05收到原稿,2015-03-20收到修改稿

∗宇航动力学国家重点实验室开放基金资助

†whb@pmo.ac.cn