太阳频率漂移的扰动层位置的变化∗
2015-06-27CHINTARUNGRUANGCHAIPattana杨伍明毕少兰谭小燕
CHINTARUNGRUANGCHAI Pattana 杨伍明 毕少兰谭小燕
(1北京师范大学天文系北京100875)
(2河南理工大学理化学院焦作454000)
太阳频率漂移的扰动层位置的变化∗
CHINTARUNGRUANGCHAI Pattana1杨伍明1,2†毕少兰1谭小燕2
(1北京师范大学天文系北京100875)
(2河南理工大学理化学院焦作454000)
太阳p模频率随太阳磁活动的变化被称为频率漂移.频率漂移被认为是起源于太阳近表面的一个薄层受到的扰动.利用磁活动指数和太阳模型来计算频率漂移的方法之前已经建立起来了.在这种方法中,频率漂移值依赖于磁活动强度和扰动源位置.磁活动强度正比于磁活动指数.扰动源的位置之前被认为是固定的.研究了扰动源位置的变化.利用观测的太阳p模震动频率和Ca II指数,发现了扰动源的位置可能是随着太阳磁活动而变化的.在太阳活动极大时,扰动源位置较深,而在太阳活动极小时,扰动源位置较浅.
太阳:震动,太阳:磁场,太阳:活动,太阳:内部
1 引言
日震学已经发展了几十年,它通过研究太阳的声波模使得我们可以去研究无法直接观测的太阳内部结构.除了p模震动,太阳还有周期性的磁活动.太阳的磁活动被认为起源于一个环向强磁场.这个环向强磁场是由作用在太阳对流区底部的某个发动机机制产生的[1−2].Woodard等[3]首先发现了太阳p模频率随磁活动的变化.随后,利用大熊湖太阳天文台的观测数据,Libbrecht等[4]确认了这种变化—频率漂移.
太阳的p模震动依赖于太阳的内部结构[5−8].太阳的频率漂移表明太阳的内部结构发生了某种变化.太阳结构的改变会影响在这一区域传播的声波.太阳周期性活动对p模频率的影响已经被许多作者研究过[9−12].Libbrecht等[4]指出在太阳活动周期间太阳的结构变化主要发生在近表面的一个薄层中,并且这个变化层(扰动层)的径向结构不随时间和纬度变化.
Metcalfe等[13]和Dziembowski[14]介绍了一种利用恒星模型计算频率漂移的方法.在这种方法中有两个重要参数:磁活动强度和扰动层的位置.许多作者已经证明了频率漂移和磁活动强度有关[15−17].Chaplin等[17]比较了伯明翰太阳观测网在3个太阳活动周期间的频率漂移和各种磁活动指数,并得出Mg II和Ca II指数可以用来估算频率漂移.假定磁活动强度和Mg II指数的比是常数和扰动层位置固定,Metcalfe等[13]计算了太阳的频率漂移,并给出扰动层位于太阳光球层以下0.3 Mm处.此外,这一方法也被用于研究其他恒星的磁活动等[18−20].
观测显示太阳的平均磁场强度随磁活动变化[21].在这项工作中,基于Metcalfe等[13]的方法,利用GONG(Global Oscillation Network Group)的数据等[22],我们研究了扰动层位置是否随太阳磁活动变化的问题.
2 GONG观测的p模频率和频率漂移
在本文中,我们利用了GONG观测给出的p模频率.GONG的p模频率是以36 d为一个观测周期给出的.36 d称为一个GONG月.GONG的观测把日面分解成许多观测区域,因此它观测到了不同n、l和m模的震动频率νnlm.我们只需要考虑中心频率νnl.中心频率定义为

为了得到频率漂移,通过对每一年内的所有GONG月的观测频率求平均,我们计算了太阳每一年的p模频率.我们把频率漂移定义为某一年的频率与2007年的频率差,即

2007年是太阳第23活动周末期的极小年.当频率大于3500µHz时误差较大,我们只使用了小于3500µHz的频率值.图1给出了l=0的模的频率漂移.从图1中可以看出,在高频处频率漂移值较大,在太阳活动极大年频率漂移值也较大.图2给出了l=0的模的平均频率漂移值随时间的变化.这些平均值是对13≤n≤24的模求算术平均得到的,显示出频率漂移是随太阳磁活动变化的.
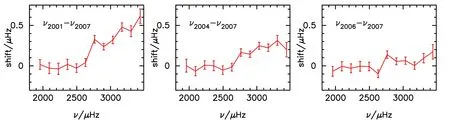
图1 l=0的模的频率漂移随频率的变化.误差棒表示1σ误差.Fig.1 Frequency shifts of modes with l=0 as a function of frequency.Error bars indicate a 1σ error.
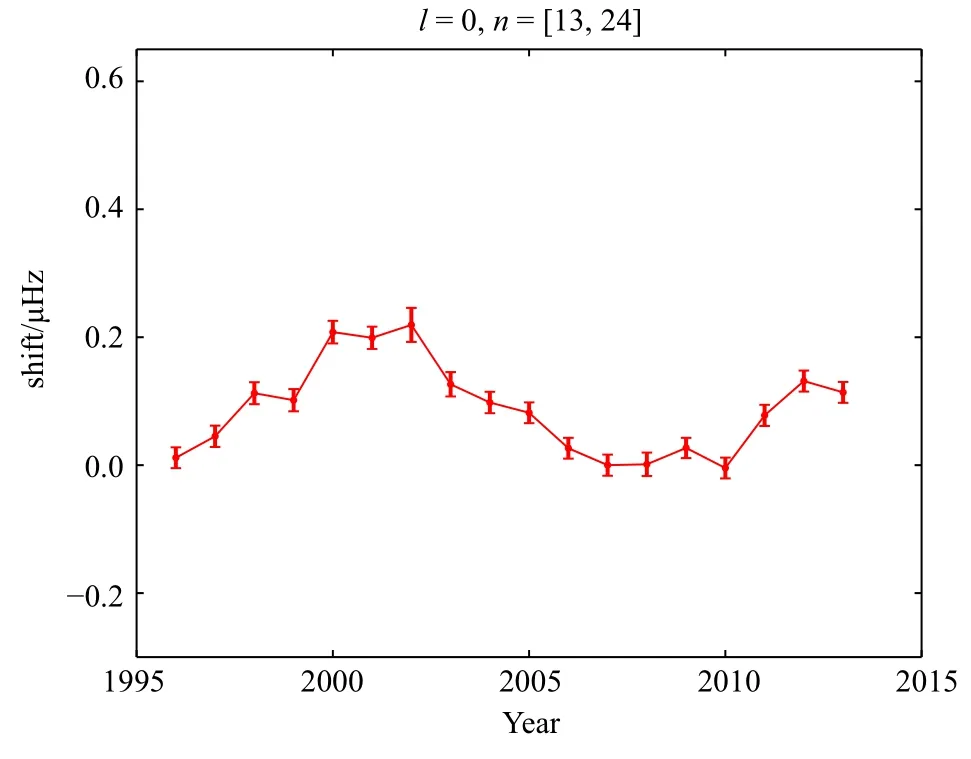
图2 l=0和n=13−24的模的平均频率漂移在1996—2013年间的变化.误差棒表示1σ误差.Fig.2Variation of the mean frequency shift of modes with l=0 and n=13−24 between 1996 and 2013. Error bars indicate a 1σ error.
3 频率漂移的扰动层的位置
由近表面扰动层引起的p模频率的变化可以由下式计算[13−14]:

其中R和M分别是以太阳值为单位的恒星半径和质量,θ0是恒星的自转轴和视线间的夹角,Ak是和磁活动强度相关的参数,Dc,k是恒星光球层以下的深度,也就是对球谐度l=k的模产生扰动的扰动层的位置.参量κk,lm由下式决定:

其中P2k(µ)是勒让德多项式,是2k阶正交多项式[23],

参量Qnl(Dc,l)定义为

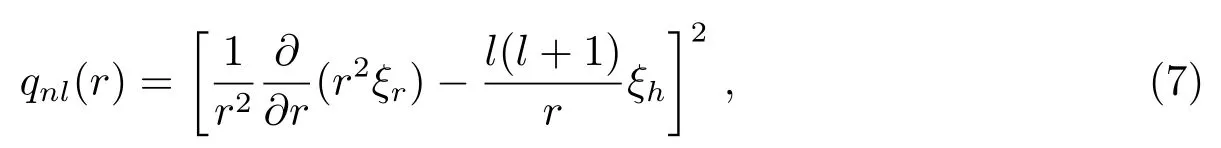
ξr和ξh表示无扰动恒星模型的p模的本征函数.
对于l=0的模,理论的频率漂移是
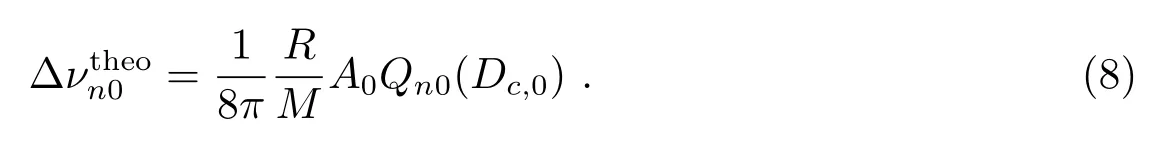
参数A0被假定成正比于Ca II指数,即对于给定的f0和Dc,0,利用(8)式,我们就能计算出恒星模型的p模频率漂移.对于观测到的恒星,我们就能确定扰动层位置Dc,0.
4 计算结果
我们使用了NSO(National Solar Observatory)观测给出的Ca II指数.对每一个给定的A0/∆iCaII,即f0,利用(8)式,我们计算了不同Dc,0下太阳模型M98[24]的.通过计算χ2,我们比较了计算得到的和观测的χ2定义为
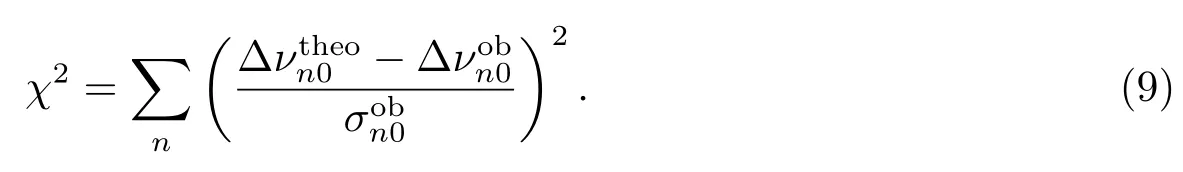
使χ2取得最小值的A0/∆iCaII就是最佳的f0. 对于一个给定的A0/∆iCaII,我们对从1996年到2013年每一年的频率漂移对应的χ2进行求和.图3给出了求和得到的χ2随A0/∆iCaII的变化. 图3显示A0/∆iCaII等于15460时χ2最小. 在整个磁活动期间,我们取f0=15460.
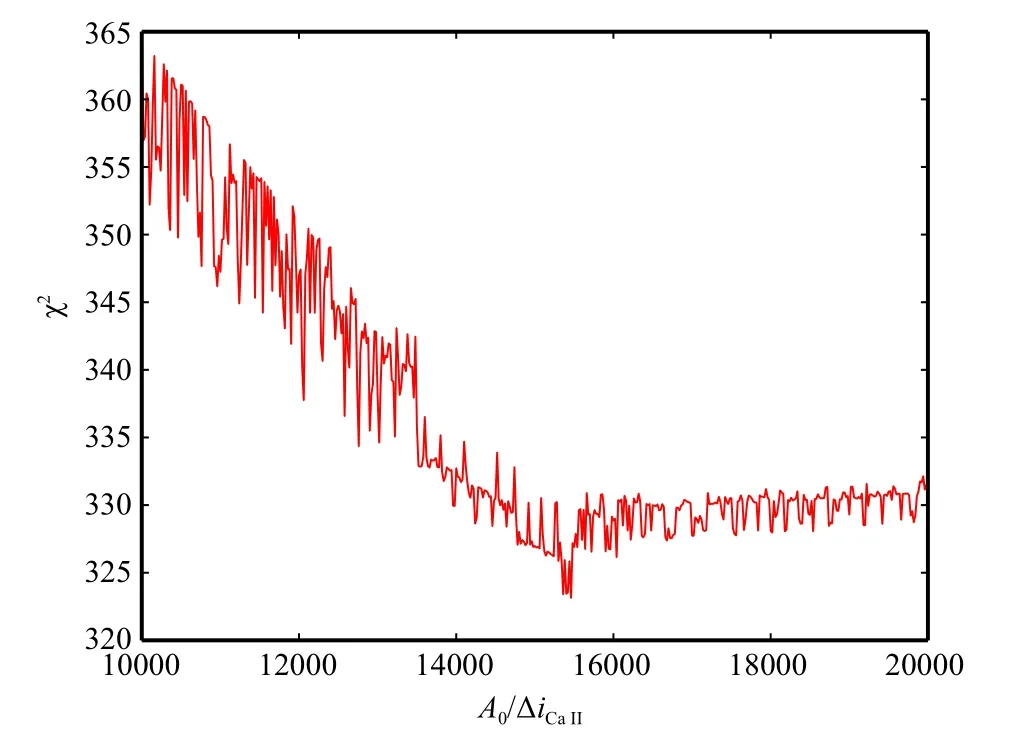
图3 求和的χ2随A0/∆iCaII的变化.χ2的最小值位于A0/∆iCaII=15460处.Fig.3 The value of total χ2as a function of A0/∆iCaII.The smallest χ2is at A0/∆iCaII=15460.
把A0/∆iCaII固定在15460上,对每一年的使得χ2极小的Dc,0被当作扰动层的最佳位置.表1给出了计算得出的每一年的A0和Dc,0.图4和图5分别给出了A0和Dc,0随时间的变化,表明A0和Dc,0是随太阳磁活动变化的.在太阳磁活动极大时的扰动源的位置Dc,0比太阳活动极小时的要深.图6给出了观测和理论计算得到的频率漂移随频率的变化.理论计算的频率漂移和观测得到的频率漂移符合得很好.

图4 太阳的∆iCaII和计算得到的A0随时间的变化.误差棒表示1σ误差.Fig.4 Solar∆iCaIIand calculated A0as a function of time.Error bars indicate a 1σ error.
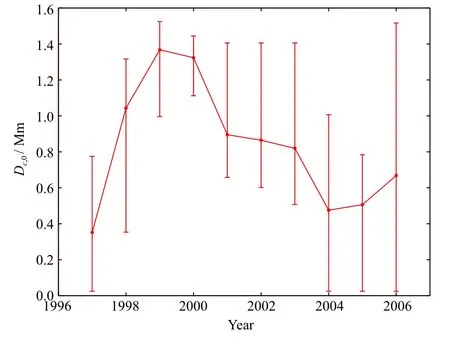
图5 计算得到的Dc,0随时间的变化.误差是根据A0的误差计算给出的.Fig.5 Calculated Dc,0as a function of time.Error bars indicate a 1σ error which is determined according to the errors of A0.

图6 观测和理论计算的频率漂移随频率的变化.左图是1998—2007年间的频率漂移.右图是2002—2007年间的频率漂移.Fig.6 Observed and theoretical frequency shifts as a function of frequency.Left panel shows the shifts between 1998 and 2007.Right panel shows those between 2002 and 2007.

表11997 —2006年的太阳的A0和Dc,0Table 1 Calculated A0and Dc,0of the Sun from 1997 to 2006
5 讨论和总结
尽管GONG有1996—2013年的观测频率,但1996年和2007—2010年接近于太阳活动极小期,这时的∆iCaII比起其误差值很小,因此我们没有计算这期间的扰动层位置.我们只计算了1997—2006年的扰动层的位置变化情况.这一时间段几乎包含了第23活动周的全部,因此应该足以用来研究扰动层位置是否随磁活动变化.
当热压强远远大于磁压时,磁场可能不足以改变太阳的结构,也就不会影响震动频率.太阳的热压强随半径增大而减小.因此扰动主要发生在近表面附近.当磁场增强时,磁场就有能力扰动具有更大热压强处的结构.太阳的整体平均磁场强度随磁活动而增大[21].因此,在太阳活动极大期扰动可以发生在较深的位置处,扰动层的位置就会随着磁活动而改变.
我们的计算结果表明导致太阳频率漂移的扰动层的位置可能是随磁活动而改变的.在太阳活动极大期,扰动层位于光球层下较深处,在太阳活动极小期,其位于较浅处.然而,对于一个固定的扰动层位置,频率漂移的值也能计算出来.扰动层位置不是唯一能解释频率随太阳活动变化的因素.
致谢这项工作使用了全球日震网(GONG)观测得到的数据.
[1]Dikpati M,Gilman P A.ApJ,2006,649:498
[2]Fan Y.LRSP,2009,6:4
[3]Woodard M F,Noyes R W.Nature,1985,318:449
[4]Libbrecht K G,Woodard M F.Nature,1990,345:779
[5]熊大闰,邓李才.天文学报,2012,53:500
[6]Xiong D R,Deng L C.ChA&A,2013,37:248
[7]熊大闰,邓李才.天文学报,2013,54:20
[8]Xiong D R,Deng L C.ChA&A,2013,37:294
[9]Goldreich P,Murray N,Willette G,et al.ApJ,1991,370:752
[10]Howe R,Komm R W,Hill F.ApJ,2002,580:1172
[11]Dziembowski W A,Goode P R.ApJ,2004,600:464
[12]Dziembowski W A,Goode P R.ApJ,2005,625:548
[13]Metcalfe T S,Dziembowski W A,Judge P G,et al.MNRAS,2007,379:L16
[14]Dziembowski W A.AIPC,2007,948:287
[15]Jim´enez-Reyes S J,R´egulo C,Pall´e P L,et al.A&A,1998,329:1119
[16]Tripathy S C,Kumar B,Jain K,et al.SoPh,2001,200:3
[17]Chaplin W J,Elsworth Y,Miller B A,et al.ApJ,2007,659:1749
[18]Metcalfe T S,Basu S,Henry T J,et al.ApJL,2010,723:L213
[19]Metcalfe T S,Buccino A P,Brown B P,et al.ApJL,2013,763:L26
[20]Liu Z,Bi S,Yang W,et al.RAA,2014,14:683
[21]Plachinda S,Pankov N,Baklanova D.AN,2011,332:918
[22]Harvey J W,Hill F,Hubbard R P,et al.Science,1996,272:1284
[23]Schou J,Christensen-Dalsgaard J,Thompson M J.ApJ,1994,433:389
[24]Yang W M,Bi S L.ApJL,2007,658:L67
Variations of the Position of Perturbation Layer of Solar Frequency Shifts
CHINTARUNGRUANGCHAI Pattana1YANG Wu-ming1,2BI Shao-lan1TAN Xiao-yan2
(1 Department of Astronomy,Beijing Normal University,Beijing 100875)
(2 School of Physics and Chemistry,Henan Polytechnic University,Jiaozuo 454000)
Variation of solar oscillation frequencies with solar magnetic activities has been investigated for many years.It is considered that the frequency shifts may be caused by a perturbation in a thin layer near the solar surface.A method for predicting frequency shifts from the changes of activity index and stellar model had been developed in previous works.In this method,the frequency shifts depend on the strength of activities and the position of the perturbation source of frequency shifts. The strength is considered to be proportional to activity index.The position of the source was assumed to be fixed previously.In this work,we investigated the change of the position of the source.By making use of observed frequencies and Ca II index of the Sun,we found that the position could change with solar activities.The position of the source is deeper during high solar activity years,but shallower during low solar activity years.
Sun:oscillations,Sun:magnetic fields,Sun:activity,Sun:interior
P144;
A
10.15940/j.cnki.0001-5245.2015.05.004
2015-01-20收到原稿,2015-04-20收到修改稿
∗国家自然科学基金项目(11273012,11273007)和中央高校基本科研业务费专项资金资助
†yangwuming@bnu.edu.cn
