计时观测测量脉冲星参数的数学模型与精度估计∗

杨廷高1,2† 高玉平1,2 童明雷1,2 赵成仕1,2 高 峰1,2,3,4

(1中国科学院国家授时中心西安710600) (2中国科学院时间频率基准重点实验室西安710600) (3中国科学院大学北京100049) (4西安科技大学应用物理系西安710054)

计时观测测量脉冲星参数的数学模型与精度估计∗

杨廷高1,2† 高玉平1,2 童明雷1,2 赵成仕1,2 高 峰1,2,3,4

(1中国科学院国家授时中心西安710600) (2中国科学院时间频率基准重点实验室西安710600) (3中国科学院大学北京100049) (4西安科技大学应用物理系西安710054)

脉冲星计时观测能够精确测量脉冲星自转参数和天体测量参数.概述了脉冲星计时模型和利用最小二乘拟合测量脉冲星各个参数并估计其方差的数学方法.在黄道坐标系导出了脉冲星各个参数误差与计时残差之间关系的数学表达式.给出了脉冲星黄经、黄纬和周年视差测量精度与脉冲星黄纬绝对值之间的关系曲线.讨论了脉冲星各个天体测量参数测量精度与脉冲星纬向参数本身的关系.

天体测量学,参考系,脉冲星,方法:解析

1 引言

脉冲星计时观测能够高精度地测量脉冲星的自转参数(脉冲星在参考历元的自转相位、频率及其导数)和脉冲星的天体测量参数(脉冲星位置、自行与周年视差).分布于天空各个方向、其自转参数和天体测量参数已经精确测定的一组脉冲星构成脉冲星时空参考架,脉冲星时空参考架作为时间和空间参考坐标具有重要应用价值.射电望远镜的脉冲星计时观测提供脉冲星脉冲到达望远镜时刻(TOA),利用同一望远镜对相同脉冲星多年观测的TOA时间序列,能够分析得到脉冲星的自转参数和天体测量参数.我们讨论利用脉冲星计时观测测量脉冲星参数的数学模型和测量精度问题.

2 脉冲星计时模型概述

在脉冲星参考架,脉冲星自转相位与其自转参数关系可表示为

式中t和t0均为脉冲星时，t0对应参考历元.ϕ0、ν和˙ν分别是t0时刻脉冲星的自转相位、频率及其1阶导数.设脉冲星钟预报的脉冲时刻是tp,P(t)是t时刻脉冲星自转周期,有

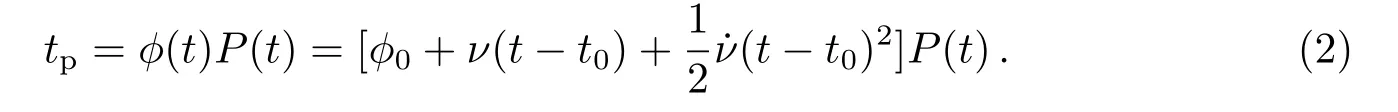
假设tobs是以原子钟为参考,地面射电望远镜观测得到的脉冲星同一脉冲的到达时刻(TOA),tobs与tp有下述关系:

式中,Δtc包括计时观测参考原子钟到地球时TT的改正和TT到质心坐标时TCB的改正,这两项改正通常采用事先计算好的数值表内插得到[1].一般说来,Δtc还应包括TCB到脉冲星时的改正.c是光速,ˆn是脉冲星在(太阳系)质心坐标系的单位矢量,→V是脉冲星相对于太阳系质心速度矢量.Δt=t−t0,即观测时刻与参考历元差值.→r是观测时刻望远镜相对于太阳系质心的位置矢量.R0是参考历元脉冲星相对于太阳系质心距离.G是牛顿引力常数,Mk是第k个太阳系天体的质量,→rk是在观测时刻望远镜相对于第k个太阳系天体位置矢量,rk是→rk的模,n是计算Shapiro延迟采用的太阳系主要天体数量. r⊙是观测时刻望远镜到太阳的距离,m⊙是太阳质量,ψ是太阳和脉冲星在观测时刻相对望远镜的张角.Δtob是脉冲双星轨道运动延迟改正,包括Roemer延迟、Shapiro延迟和Einstein延迟改正等[2−3].(3)式中,tobs(观测得到的TOA)和→r(望远镜相对于太阳系质心矢量)为已知量,其中→r由已知的望远镜相对于地心矢量和地心历表计算得到.脉冲星在参考历元t0的自转相位ϕ0、自转频率ν及其导数˙ν是待求的自转参数.对于毫秒脉冲星,自转频率的2阶导数可以忽略,但对于自转较慢的普通脉冲星,自转参数还应该包括自转频率的2阶及其以上导数.脉冲星位置矢量(包括方向和距离)以及自行是待求的天体测量参数.脉冲星计时观测只能测量自行,不能测量视向速度.对于脉冲双星,待求的参数还应该包括脉冲星的轨道参数.(3)式是脉冲星计时观测方程的精确数学模型[4].

3 脉冲星参数最小二乘拟合与精度估计

通常脉冲星参数的近似值总是知道的,将参数(包括自转参数和天体测量参数)近似值作为采用值分别代入(2)式和(3)式,利用脉冲星的长期计时观测得到的TOA时间序列(n个TOA),可以计算得到每个TOA的计时残差,计时残差的系统性变化是由脉冲星参数误差所致.利用脉冲星计时残差(称为拟合前残差)采用最小二乘拟合,得到脉冲星参数采用值的改正值及其方差.最小二乘拟合需要将非线性方程(3)在各个参数采用值处进行级数展开,从而把(3)式转换成包含脉冲星天体测量参数采用值误差的线性方程.将(2)式表示成脉冲星自转参数误差的线性方程.假设向量→R是拟合前的计时残差,脉冲星自转参数和天体测量参数采用值的误差向量为→P,脉冲星参数的系数矩阵(也称为计时模型矩阵)为M,如果观测TOA数量为n,脉冲星自转参数和天体测量参数总数量为m(n＞m),则M是n×m的矩阵.用矩阵表示的最小二乘拟合的线性方程为

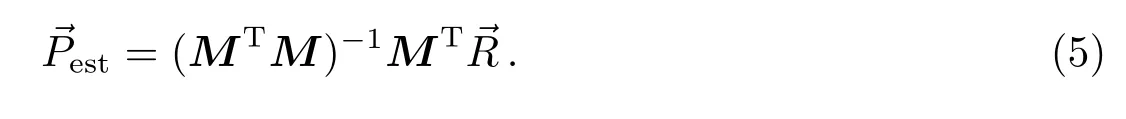
脉冲星参数估计值的协方差矩阵是

(6)式中σ是TOA测量误差.由于TOA测量误差不一定能反映拟合后计时残差的均方根(rms)误差,考虑到最小二乘采用的TOA数量与被估计的参数数量,实际给出的协方差矩阵是

(7)式表示的协方差矩阵中,主对角线元素是脉冲星被估计参数的方差,主对角线上下元素对称,它们是脉冲星参数之间的协方差.在TOA测量精度不一致的情况下,通常采用加权最小二乘法拟合脉冲星参数.类似地,可以写出加权最小二乘的脉冲星参数估计及其协方差的矩阵表达式,详情可参阅文献[5].

应该指出的是,只有在脉冲星参数采用值误差非常小的情况下,采用线性最小二乘才能够得到脉冲星参数的精确估计,因为(3)式的线性方程忽略了高阶项,只能看作是近似方程,脉冲星参数采用值误差越小,(3)式的线性表达式越精确.因此,实际的脉冲星参数拟合是采用逐步逼近的迭代方法.每次拟合后,需要检查拟合后计时残差,如果存在任何系统性变化趋势,则修正相关的脉冲星参数采用值后,重新拟合,直到得到满意的结果为止[6].下面,我们讨论脉冲星计时残差与脉冲星参数采用值误差之间的数学关系.

4 脉冲星计时残差与自转参数误差的数学关系

对(2)式进行微分,有

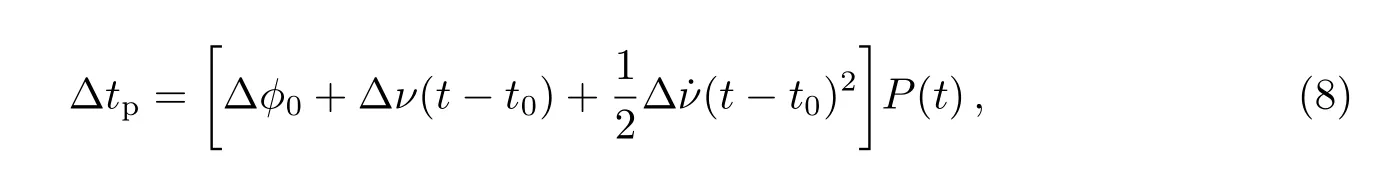
计时残差是“模型－观测”,(8)式中Δtp就是脉冲星自转参数采用值误差引起的计时残差. (8)式描述了计时残差与脉冲星在参考历元t0的自转相位ϕ0、频率ν及其1阶导数˙ν采用值误差之间的数学关系.ϕ0误差Δϕ0使得计时残差产生常数偏差,ν误差Δν引起计时残差线性变化,˙ν误差Δ˙ν使得计时残差呈现二次曲线变化.因为我们通常并不知道脉冲星自转参数的精确值,只能根据计时残差变化特征拟合得到精确的脉冲星自转参数.

5 脉冲星计时残差与位置、自行误差的数学关系

下面我们导出脉冲星位置、自行参数误差与脉冲星计时残差的关系表达式.脉冲星位置和自行误差影响Roemer延迟.由(3)式可知,Roemer延迟项为−→r·ˆn/c=−(→s+→rE)·ˆn/c,式中→r是望远镜相对于太阳系质心SSB的矢量,→s是望远镜相对于地心矢量,→rE是地心相对于SSB的位置矢量,ˆn是脉冲星单位矢量,c是光速.因为脉冲星位置和自行误差对脉冲TOA从望远镜到地心转换的影响非常小,可以忽略[7].研究脉冲星位置和自行误差对Roemer延迟的影响,主要考虑TOA从地心到太阳系质心SSB转换的Roemer延迟,有

在黄道坐标系内,脉冲星的位置为黄经λ、黄纬β,脉冲星单位矢量令脉冲星黄经自行为µλ、黄纬自行为µβ,参考历元t0时刻脉冲星的位置为λ0和β0,则与t0的差值为t的时刻,脉冲星的黄经、黄纬分别为λ=λ0+µλt和β=β0+µβt,则有

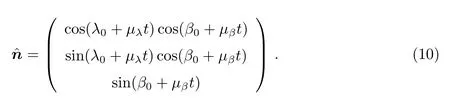
假设地球绕SSB的周年运动轨道为圆轨道,因为我们的目的是计算脉冲星位置误差对Roemer延迟的影响,将地球公转轨道视为圆轨道是安全的[7].地心到SSB的平均距离R=1 au,令t时刻地心沿黄道面公转位置角为ωt,ω=2π/yr,则地心在黄道坐标系的位置矢量为

将(10)式和(11)式代入(9)式,做矩阵乘运算,并将三角函数进行级数展开,忽略二次以上高阶项(这些项都是小量),整理后得到

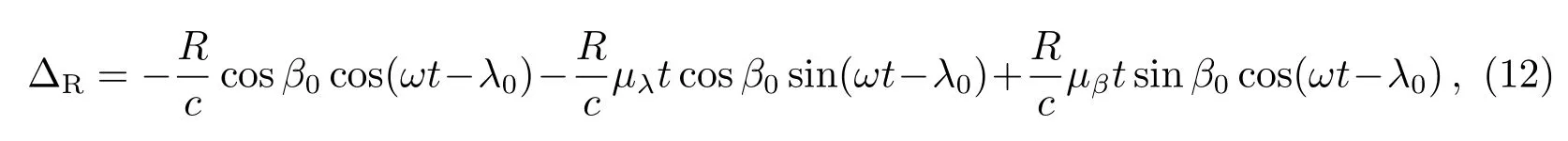
在(12)式中,λ0、β0的单位是rad,µλ和µβ的单位是rad/yr.应用(12)式对β0求偏导数,我们得到

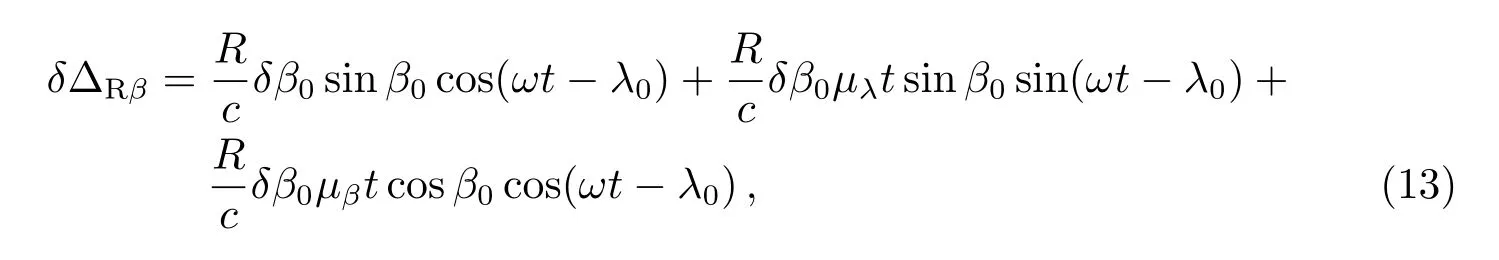
(13)式中,δΔRβ是黄纬β0的误差δβ0对计时残差的影响,右边第2项包括乘积δβ0µλ,是小量,可以略去,右边第3项包括乘积δβ0µβ,同样是小量,可以略去.于是(13)式变成

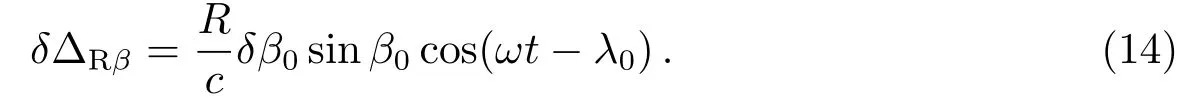
应用(12)式对λ0求偏导数,略去高阶小量项,有

(15)式中δΔRλ是黄经λ0误差δλ0对计时残差的影响.应用(12)式对µβ求偏导数,有

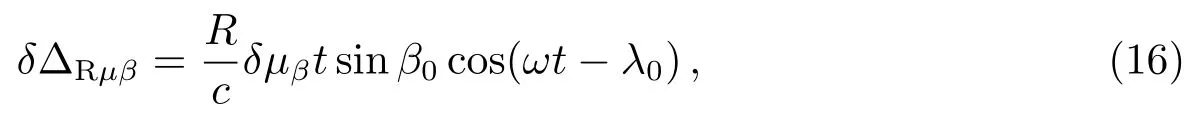
(16)式中δΔRµβ是黄纬自行µβ误差δµβ对计时残差的影响.应用(12)式对µλ求偏导数,有

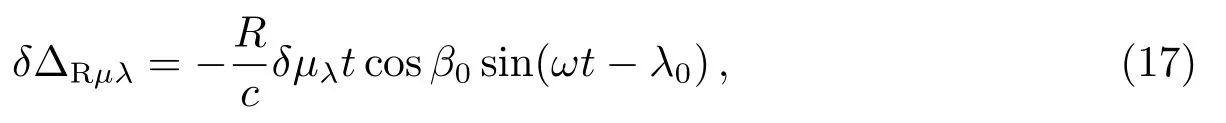
(17)式中δΔRµλ是黄经自行µλ误差δµλ对计时残差的影响.

由(14)式至(17)式可以看出,脉冲星黄纬误差导致计时残差按周期为1 yr的余弦曲线变化;脉冲星黄经误差导致计时残差按周期为1 yr的正弦曲线变化;脉冲星黄纬自行误差导致计时残差按周期为1 yr的余弦曲线变化,且幅度随时间线性增加;脉冲星黄经自行误差导致计时残差按周期为1 yr的正弦曲线变化,且幅度随时间线性增加.

利用长期的TOA观测资料,采用最小二乘法拟合确定脉冲星的黄道坐标位置和自行参数.脉冲星位置和自行误差导致计时残差周期性变化,根据计时残差的变化特征,可以修正脉冲星的有关天体测量参数,重新拟合,直到计时残差没有周年性变化趋势,从而获得精确的脉冲星天体测量参数为止.假设TOA精度为σ,数量为n,根据误差传递理论,脉冲星黄经、黄纬及其自行测量精度分别可表示为下面的比例关系表达式:从以上公式还可以看出,脉冲星位置和自行测量精度与脉冲星的纬向参数本身有关.

6 脉冲星计时残差与周年视差误差的数学关系

下面我们讨论脉冲星周年视差误差与计时残差的关系.由(3)式,视差延迟项为该式中R0是脉冲星到太阳系质心SSB的距离,是脉冲星单位矢量,望远镜相对于SSB矢量是测站相对于地心矢量,是地心相对于SSB矢量.由于矢量→s影响,脉冲星视差误差导致的时间延迟是小量,可以忽略,我们只考虑→rE的视差延迟效应.于是视差延迟Δp可写为

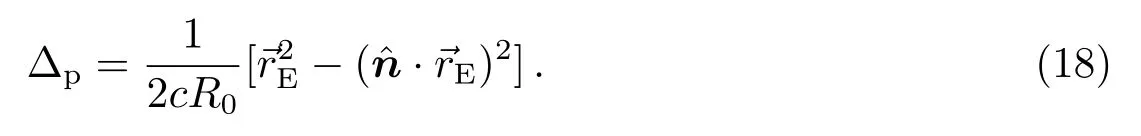
脉冲星视差π=R/R0,π的单位是rad(以下π均指视差).将π=R/R0代入(18)式,有

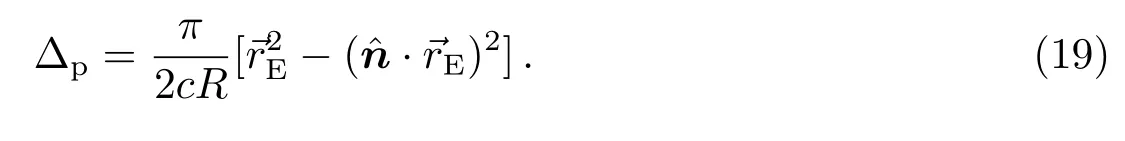
将(10)式和(11)式代入(19)式,做矩阵乘运算,并将三角函数进行级数展开,忽略二次以上高阶项(这些项都是小量),整理后得到

应用(20)式对π求偏导数,有

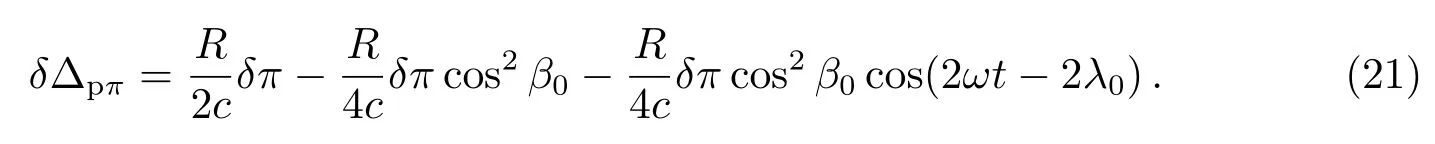
(21)式中δΔpπ是周年视差π的误差δπ引起的计时残差,前两项是常数项,由第3项可看出, δπ导致计时残差按照周期为半年的余弦曲线变化.视差π的误差对计时残差影响,具有与其他天体测量参数不同的特征.根据脉冲星计时残差中存在的周期为半年的余弦曲线变化趋势,修正视差π的采用值,重新拟合计时残差,直到残差不再存在半年周期余弦曲线变化趋势为止,从而拟合得到精确的视差π值.实际上脉冲星位置、自行和视差参数误差对计时残差影响,还有脉冲星自转参数误差对计时残差影响,是按照时间t叠加在一起的,虽然它们具有可识别的不同特征,但在实际参数拟合时的经验判断也非常重要.

利用长期的TOA观测资料,采用最小二乘法拟合确定脉冲星的周年视差参数.假设脉冲星TOA观测序列包含n个TOA,TOA的观测精度为σ,根据误差传递理论,由(21)式可知,脉冲星周年视差的测量精度

7 讨论

利用射电望远镜的计时观测,能够高精度地测量脉冲星自转参数和天体测量参数.脉冲星参数测量需要高精度原子时作参考,目前,最好用地球时TT作脉冲星计时观测的参考时间尺度[8].脉冲星天体测量参数的测量精度与脉冲星的纬向参数本身数值有关.假设脉冲星TOA观测精度约1µs,TOA采样间隔约5 d,射电望远镜计时观测3 yr,利用上文给出的有关表达式,计算得到脉冲星黄经、黄纬和周年视差测量精度与脉冲星黄纬β绝对值的关系曲线,并分别绘于图1.在图1中,横坐标是脉冲星黄纬的绝对值|β|(单位:◦),脉冲星黄经、黄纬和周年视差测量精度曲线分别为σλ、σβ和σπ(单位:mas).脉冲星黄经自行测量精度与脉冲星黄纬绝对值之间的关系与σλ曲线变化趋势相同;脉冲星黄纬自行测量精度与脉冲星黄纬绝对值之间的关系与σβ曲线变化趋势相同.由图1可见,同一射电望远镜对不同脉冲星的参数测量精度不相同,与脉冲星的纬向参数绝对值有关,并具有小的盲区;纬度接近0◦的星不能测其纬度,纬度绝对值接近90◦的星不能测量其经度和周年视差.随脉冲星纬度绝对值的增加,其周年视差的测量精度下降得更快.

安装于不同地理位置的射电望远镜有利于观测不同天区的脉冲星,但图1所示脉冲星天体测量参数测量精度曲线适用于任何地面射电望远镜.进一步改进TOA测量精度、增加TOA采样密度、扩大TOA序列的时间跨度,能够提高脉冲星参数测量精度.但对位于测量盲区的脉冲星,只能用其他观测技术获得其高精度天体测量参数.

从脉冲星计时残差与脉冲星参数误差的关系表达式,我们还可看出:脉冲星计时观测参考的时间尺度如果具有线性、二次性或周年性变化系统误差,在最小二乘拟合时,这种线性、二次性误差会被不同程度地吸收到脉冲星自转参数中去,周年性误差会被吸收到天体测量参数中去.计时观测参考的地球历表如果有线性、二次性或周年性系统误差,也会对拟合得到的脉冲星参数产生影响.所以,计时观测测量脉冲星参数,应该采用高精度的原子时系统(如TT时间系统)和高精度的近代地球历表作参考.

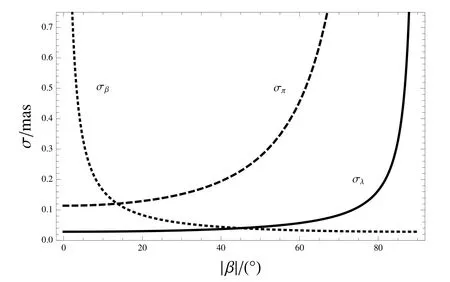
图1 脉冲星黄经、黄纬和周年视差测量精度与黄纬绝对值之间关系Fig.1 The relationship between precision of ecliptic longitude,latitude,and annual parallax of pulsars versus absolute ecliptic latitude of pulsars

关于脉冲双星轨道参数的测量问题,其测量原理方法与脉冲星自转参数和天体测量参数类似.双星轨道参数误差会导致计时残差的系统性变化,不同轨道参数误差对计时残差的影响具有各自可识别的特征,它们都是脉冲星轨道周期的函数.为测量脉冲星轨道参数,对于脉冲双星的TOA测量,必须在其轨道周期上加密采样,以便拟合得到满意精度的双星轨道参数.

[1]Irwin A W,Fukushima T.A&A,1999,348:642

[2]Damour T.AnIHP,1986,44:3263

[3]Taylor J H,Weisberg J M.ApJ,1989,345:434

[4]Edwards R T,Hobbs G B,Manchester R N.MNRAS,2006,372:1549

[5]Coles W,Hobbs G,Champion D J,et al.MNRAS,2011,418:561

[6]Hobbs G B,Edwards R T,Manchester R N.MNRAS,2006,369:655

[7]Madison D R,Chatterjee S,Cordes J M.AJ,2013,777:2

[8]Guinot B,Petit G.A&A,1991,248:292

Mathematical Model for Measuring Pulsar Parameters and Precision Estimation with Pulsar Timing Observations

YANG Ting-gao1,2GAO Yu-ping1,2TONG Ming-lei1,2ZHAO Cheng-shi1,2GAO Feng1,2,3,4
(1 National Time Service Center,Chinese Academy of Sciences,Xi’an 710600) (2 Key Laboratory of Time and Frequency Primary Standards,National Time Service Center,Chinese Academy of Sciences,Xi’an 710600) (3 University of Chinese Academy of Sciences,Beijing 100049) (4 Department of Applied Physics,Xi’an University of Science and Technology,Xi’an 710054)

Pulsar rotational and astrometric parameters can be measured with a very high precision by pulsar timing observations.The pulsar timing model,the estimation method of pulsar parameters and their covariances by least square solution are brie fl y described.The relationship between the timing residuals of a pulsar and errors of its rotational parameters is denoted with the polynomial of time.The relationship between the timing residuals of a pulsar and errors of its astrometric parameters can be derived from the Roemer delay due to the Earth motion around the solar system barycenter. The mathematical expressions for the relationship between timing residuals and errors of pulsar astrometric parameters adopted for timing solution are derived within the ecliptic coordinate reference system using the transformation from analytical vector expression of the Roemer delay to the corresponding spherical coordinate expression. The precision of pulsar astrometric parameters determined by timing observation is dependent on the absolute ecliptic latitude of pulsar.For the pulsar located close to the ecliptic plane,it is difficult to precisely measure the pulsar latitude parameter by timing observations.For the pulsar located close to the ecliptic pole,it is difficult to precisely measure the pulsar longitude and annual parallax parameters by timing observations.The precision of pulsar ecliptic coordinate and annual parallax parameters determined by timing observations versus pulsar absolute ecliptic latitude is shown.The relationship between the precision of proper motion parameters of pulsar measured by timing observations and pulsar absolute latitude is also discussed.

astrometry,reference system,pulsar,methods:analytical

P127;

:A

2014-11-28收到原稿,2015-03-24收到修改稿

∗国家自然科学基金项目(11103024,11373028,11403030)、中国科学“西部之光”人才培养计划西部博士项目(中国科学院人教[2011]180号)和西部之光–联合学者项目(2010LH02)资助

†yangtg@ntsc.ac.cn

10.15940/j.cnki.0001-5245.2015.04.007