基于量子模糊聚类算法的复杂网络社团结构探测

牛艳庆

(中南民族大学 数学与统计学学院，武汉 430074)

基于量子模糊聚类算法的复杂网络社团结构探测

牛艳庆

(中南民族大学 数学与统计学学院，武汉 430074)

研究了复杂网络的社团结构特性，探讨了复杂网络的社团结构探测算法.针对现有算法中判断社团结构时的主观性问题，提出了量子模糊聚类算法，并将该算法用于复杂网络社团结构的探测.实验结果表明：该算法可以准确、有效地探测到网络中实际存在的社团结构.

复杂网络；社团结构；量子模糊聚类

复杂网络是一个包含了大量个体以及个体之间相互作用的系统，通常把个体视为网络中的节点，把个体间的相互作用视为网络节点与节点之间的连接，这样由大量的节点以及节点间的连接所构成的复杂系统，就称为复杂网络.近年来的研究表明，大量的真实网络是由若干个群或团组成，这样的群或团被称为社团结构[1]，而且每个社团结构内部的节点之间的连接较为紧密，社团之间的连接却稀疏得多.因而，社团结构是反应复杂网络结构性质的重要特征.对于大量存在的具有社团结构的复杂网络，采用一些恰当的方法，准确而有效地探测出其中的社团结构，是复杂网络研究中的一个重要课题.

聚类分析方法[2]是一种无监督学习方法，通过选择合适的参数，确定聚类中心和样本的聚类数目，研究样本的分布情况.我们以聚类分析的思想为基础，提出了量子模糊聚类算法，用于复杂网络社团结构的探测.在经典的空手道俱乐部网络的实验结果表明，该方法能够准确并且有效地探测复杂网络中的社团结构.

1 量子模糊聚类算法

1.1 量子模糊聚类算法的基本思想

模糊聚类方法[2]是应用模糊数学方法进行聚类的分析方法，因其算法设计简单、解决问题范围广、易于计算机实现，被应用于很多领域.

针对模糊聚类方法在应用时存在的局限性，我们提出了量子模糊聚类算法，主要思想是在量子空间中对数据样本进行聚类分析.该算法首先利用一个非线性映射，将原空间的待分类样本映射到一个高维的特征空间(量子空间)中，使得样本在量子空间中变得线性可分，然后在量子空间中进行聚类.这个非线性映射我们选取的是由薛定谔微分方程确定的量子势能函数[3,4].由于这个量子势能函数是连续和光滑的，那么在量子空间中，样本的拓扑结构和顺序将会被保持.因此，在原空间中聚在一起的点，在量子空间中也将会聚在一起，而且通过非线性映射，突出了不同类别样本特征的差异，使得原来线性不可分的样本点在量子空间中变得线性可分.利用该算法进行复杂网络社团结构的探测可以减少聚类误差，获得较好的聚类效果.

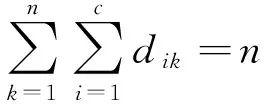
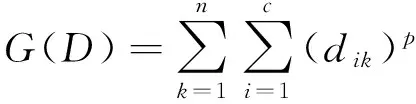
(1)

其中V(·)为量子势能函数[4]，即：

(2)

d为样本空间的维数， E是能量特征值.假定minV=0，则E的取值为：

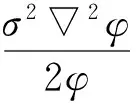
(3)

其中波函数φ(x)可以近似为：

(4)

我们利用函数V(·)将数据样本映射到量子空间，D=(dik)为模糊隶属度矩阵或划分矩阵，X={x1,x2,…,xn}为数据样本，ci为数据样本的聚类中心，c为类别个数.利用拉格朗日乘数法可得：

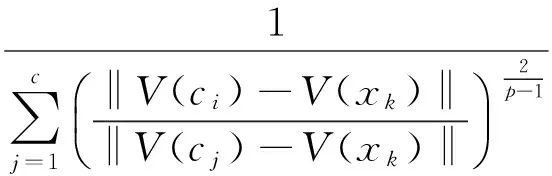
(5)

其中i=1,2,…，c,k=1,2,…,n，V(ci)按照如下方法计算：

(6)

由u的任意性知：

(7)

故可得：

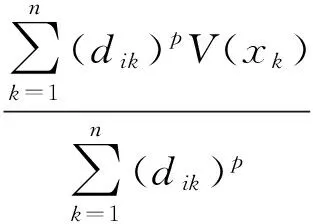
(8)

1.2 量子模糊聚类算法的迭代过程

根据以上公式的推导结果，我们可以得到量子模糊聚类算法的迭代过程为：

1) 设定聚类类别数c、加权系数p和核尺度参数σ，初始化模糊隶属度矩阵D=(dik)，及给定一个足够小的迭代截止误差ε>0；

2) 根据(5)式更新模糊隶属度矩阵或划分矩阵D=(dik)；

3) 根据(8)式计算量子势能函数在聚类中心ci处的值V(ci)；

4) 如果‖Dnew-Dold‖<ε，则终止迭代，得到要求的最优的聚类中心ci和最优划分矩阵D=(dik)，否则转到步骤2)继续进行.

2 数值实验

我们将量子模糊聚类算法用于复杂网络社团结构的探测，选取的实验数据为经典的真实网络数据，即空手道俱乐部网络数据[5].

2.1 空手道俱乐部网络

Zachary W W[6]所研究的空手道俱乐部网络被广泛应用于探测复杂网络社团结构的方法中.该网络包括34个节点和78条边，分别表示的是空手道俱乐部的成员和俱乐部成员之间的相互联系.由于俱乐部的两个管理者之间产生分歧，导致这个俱乐部以这两个管理者为中心，最终分裂为两个社团.图1为空手道俱乐部的网络，其中节点1和节点34分别表示两个管理者.

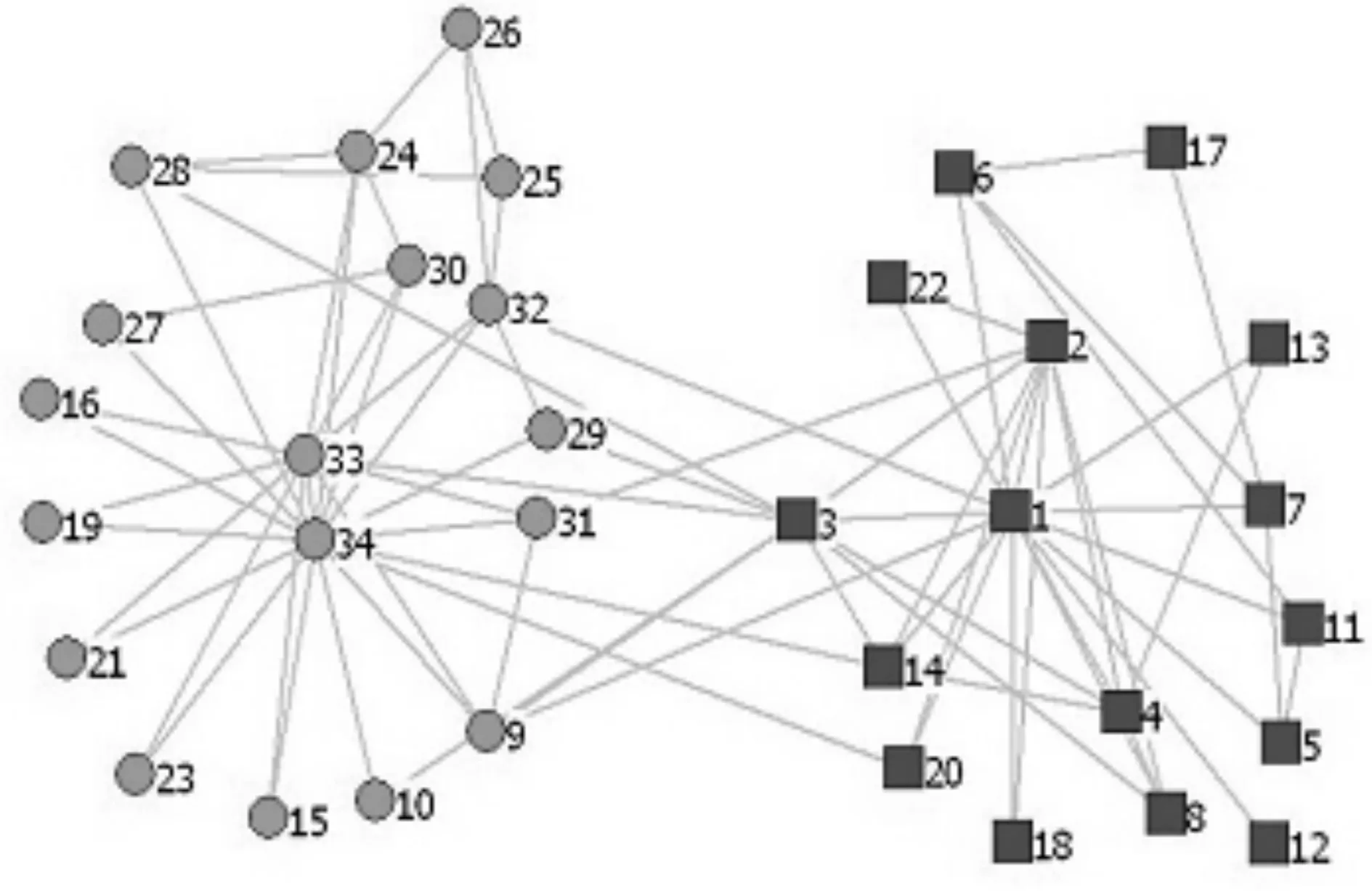
图1 空手道俱乐部网络Fig.1 Karate club network

2.2 算法的评价指标

模块度函数Q的值是评价网络中的社团结构是否明显的重要指标[7]，可以将Q值的大小用于比较不同的探测算法.Q的取值为0≤Q≤1，Q越接近于1，说明算法得到了较好的划分结果，该网络具有明显的社团结构.大量的研究表明，在实际网络中，Q值通常位于0.3～0.7之间，过大或过小的Q值很少出现.

模块度函数Q的计算方法[7]为：

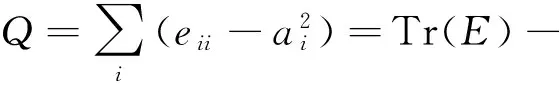
(9)

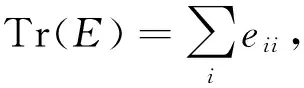
2.3 结果与分析

Newman的最短路介数算法[8]中指出，最优聚类数目的确定依靠树状图在不同位置处的截取，并依靠对应的模块度函数Q的最大值选取相应的社团结构的分类.Newman算法选择的最优聚类数目即社团结构的数目是k=4，对应的模块度函数Q的最大值为Q=0.36654.虽然社团结构的数目为4时对应的模块度函数Q的值为最大，但是这样划分得到的社团结构与实际的两个社团结构不相符合.

我们提出的基于量子模糊聚类算法的社团探测方法的主要任务是通过最大化Q值，确定最优核尺度参数σ，进而确定聚类中心，最终找到社团结构的最优划分.

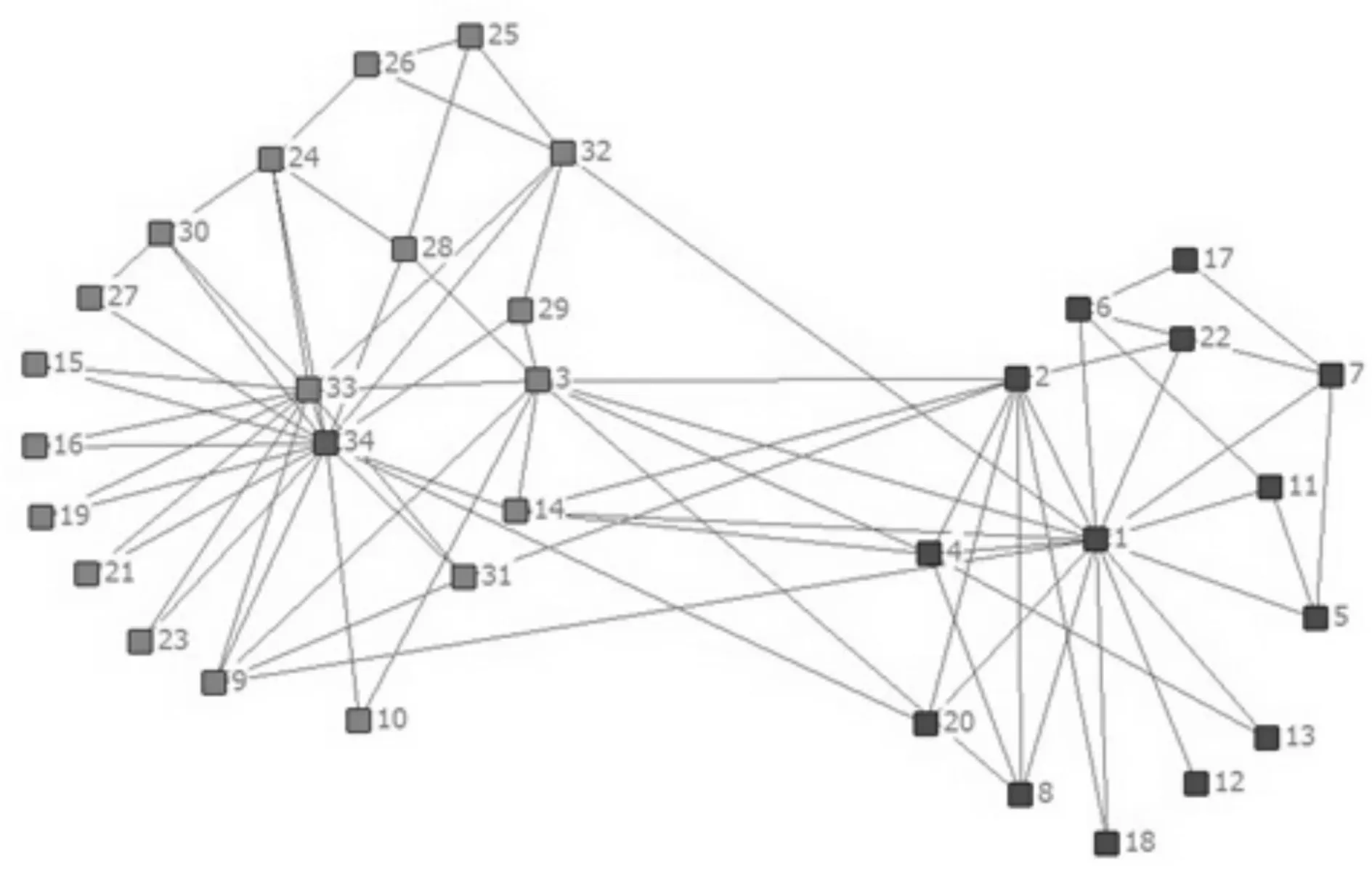
图2 本文算法得到的空手道俱乐部网络Fig.2 Karate club network by our algorithm

我们提出的基于量子谱聚类算法的社团探测方法得到的最优的社团结构的数目k=2，对应的模块度函数Q的值为Q=0.36235.图2展示了由我们的算法得到的空手道俱乐部网络的社团结构图.从图2可以看到，空手道俱乐部网络被分为两个社团，这符合实际情况，并且网络中只有节点3和 14被错误的划分，算法的准确率为94%.

3 结语

本文提出了量子模糊聚类算法，进行社团结构的探测.应用于经典的空手道网络数据的实验表明，我们的算法可以准确并且有效地探测到网络中实际存在的社团结构.我们希望能将这一算法推广到有权重和有方向的复杂网络中.

[1] Newman M. The structure and function of complex networks[J]. SIAM Review, 2003, 45(2): 167-256.

[2] 胡宝清. 模糊数学理论基础[M]. 武汉: 武汉大学出版社, 2004: 162-169.

[3] Horn D, Gottlieb A. Algorithm for data clustering in pattern recognition problems based on quantum mechanics[J]. Physical Review Letters, 2002, 88(1): 1-4.

[4] Horn D, Axel I. Novel clustering algorithm for microarray expression data in a truncated SVD space[J]. Bioinformatics, 2003, 19(9): 1110-1115.

[5] Newman M. Fast algorithm for detecting community structure in networks[J]. Physical Review E, 2004, 69(6): 066133.

[6] Zachary W W. An information flow model for conflict and fission in small groups[J]. Journal of Anthropological Research, 1977, 33: 452-473.

[7] Newman M. Detecting community structure in networks[J]. European Physical Journal B, 2004(2): 321-330.

[8] Newman M, Girvan M. Finding and evaluating community structure in networks[J]. Physical Review E, 2004, 69(2): 026113.

Detecting the Community Structure in Complex Networks Based on Quantum Fuzzy Clustering Algorithm

NiuYanqing

(College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China)

Research in this paper aims to find some novel approaches to detecting the community structures in complex networks. To reduce the subjectivity in the existing algorithms, we detect community structure in complex networks based on quantum fuzzy clustering analysis method. The experimental results show that this method can give satisfactory results.

complex networks; community structure; quantum fuzzy clustering

2015-01-25

牛艳庆 (1979-)，女，讲师，博士，研究方向：智能计算，E-mail: niuyanqing2005@hotmail.com

国家自然科学基金资助项目(11226267)；深圳市发展基金资助项目(JCYJ20130401160028781)

O159

A

1672-4321(2015)03-0123-03