永磁同步电机转矩脉动占空比最优控制方法

齐美星，童敏明

（1.苏州市职业大学电子信息工程学院，江苏苏州215104；2.中国矿业大学信息与电气工程学院，江苏徐州221006）

1 引言

矢量控制［1］（field oriented control，FOC）和直接转矩控制［2］（DTC）是目前广泛使用的两种高性能交流电机控制方案。与FOC相比，DTC具有动态响应快、系统结构简单和参数鲁棒性强等优点［3-4］。然而，传统的DTC 采取两个滞环比较器以及一个启发式的查找表来获取最优电压矢量，上述方式在数字系统实现时将产生明显的转矩脉动、系统噪声以及变化的开关频率。

为改善传统DTC 存在的转矩脉动问题，大量学者进行了深入研究，并提出了很多改进控制方案。文献［5-7］提出了一种基于空间矢量调制（space vector modulation，SVM）的DTC 方法，该方法通过输出连续的电压空间矢量，可以有效地改善电磁转矩脉动问题，同时保持一个固定的开关动作频率。多种方法可以实现内环调制电压的输出，其中包括：PI 控制［5］、无差拍控制［6］、滑模控制［7］等。上述方法在优化转矩脉动的同时，再次引入了旋转坐标变化和SVM，丢失了传统DTC 方法结构简单、鲁棒性强的优势。文献［8-9］中使用模糊控制器代替传统DTC 系统中的开关查找表，有效地降低了电机转矩脉动现象，然而模糊控制器需要对其各变量的隶属度函数进行配置，上述过程存在较大的盲目性和主观性，隶属度配置不当将直接影响系统的控制性能。此外，模糊控制存在在线运算量过大问题，给实际数字系统实现提出更高的要求。

针对传统DTC 方法存在的转矩脉动问题，本文在建立永磁同步电机（PMSM）调速系统数学模型的基础上，分析了传统DTC 方法产生转矩脉动的主要原因，进而提出一种基于占空比优化的PMSM 转矩脉动抑制方法。该方法采取主电压矢量和零电压矢量组合的方式，以控制周期内转矩脉动最优为目标进行最优占空比分配。实验结果表明，该方法在保留传统DTC 高动态响应的基础上，可以减小电磁转矩脉动、固定开关动作频率，有效地提升了PMSM 调速系统的稳态性能。

2 系统数学模型

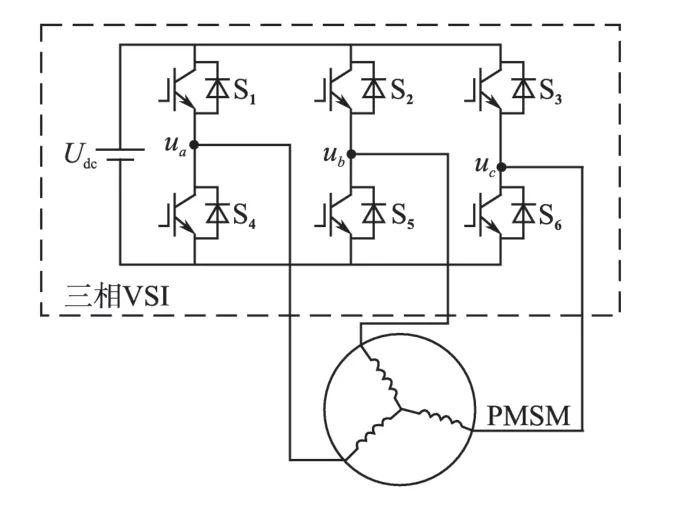
图1 三相电压型PMSM调速系统主电路Fig.1 The structure chart of PMSM speed control system driven by VSI

图1 为三相电压型PMSM 调速系统主电路，其中ua，ub，uc为逆变器三相输出端口电压；Udc为直流母线电压，S1～S6表示功率开关器件对应开关状态。在两相静止αβ坐标系下建立PMSM 调速系统电压、磁链方程为

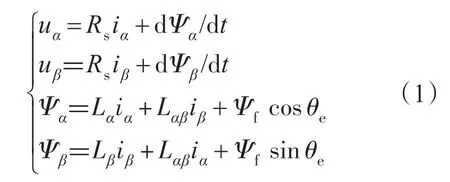
式中：uαβ，iαβ分别为αβ轴定子电压和定子电流；Rs为定子电阻；θe为转子电角度；Ψf为转子永磁体磁链。

由于面贴式永磁同步电机的Ld＝Lq＝Ls，其数学模型可以被进一步简化为复矢量形式

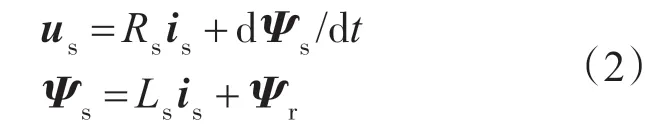
式中：us，is分别为定子电压矢量和定子电流矢量；Ψs，Ψr分别为定子磁链矢量和转子磁链矢量。

电磁转矩方程为

式中：Te为电机电磁转矩；p为电机极对数；Ψαβ为αβ轴定子磁链。

对于如图1 所示的三相电压源型逆变器系统，其可提供8种不同的电压空间矢量，包含6个非零电压矢量，2 个零电压矢量。电压空间矢量作为DTC系统中的唯一可控量，需要分析其与电磁转矩之间的对应关系，对式（2）的转矩项进行微分处理可得

求解式（2）可得定子电流矢量的变化率为

将式（2）、式（5）代入式（4）可得非零电压矢量对应电磁的转矩变化率s1为

分析式（6）可知电磁转矩变化率由3 部分组成，其中：第1 部分ΔTe1始终为负值，当负载转矩固定时ΔTe1保持不变；第2 部分ΔTe2同样为负值，其值与转速呈正比关系；第3部分ΔTe3为正值，其直接反应了定子电压对电磁转矩的影响，综上可知，当零电压矢量被选取时，由于其定子电压幅值为零，此时对应的电磁转矩变化率s2为

分析式（7）可知，s2中仅包含ΔTe1和ΔTe2两部分，且其值均为小于零，因此零电压矢量将减小电磁转矩。

3 传统DTC原理

传统DTC 利用滞环控制器进行转矩和磁链的控制，滞环控制器根据转矩和磁链误差确定其期望的增减状态，随即查询表1 所示的开关查找表，结合定子磁链所处扇区号即可确定最终输出的电压矢量，其对应的矢量选择和扇区划分原则如图2 所示。传统DTC 在每个控制周期内仅输出单一的电压矢量，如图3 所示给出了传统DTC 单一电压矢量作用效果示意图。由图3 可知，采用上述单一电压矢量控制时，在整个控制周期中转矩、磁链、电流等控制量均沿同一个变化趋势变化。当实际转矩误差较小时，所选取的电压矢量在一个控制周期的较短时间内即使转矩到达期望值，在剩余的时间内由于不存在电压矢量的转换，所选电压矢量仍作用于电机，致使转矩沿原来的方向继续变化，造成较大的转矩脉动。

表1 传统DTC开关查找表Tab.1 Switching table for conventional DTC

图2 传统DTC矢量选择和扇区划分原则Fig.2 Vector selection and sector division for conventional DTC

图3 传统DTC单一电压矢量作用效果示意图Fig.3 Traditional DTC single voltage vector effect

4 占空比优化DTC原理

传统DTC 在每个控制周期内将单一的电压矢量作用整个控制周期，此举极易造成对电机转矩调节力度过强或过弱，直接表现为稳态时的转矩脉动现象。根据式（7）分析可以看出，零电压矢量产生的转矩变化率相对较小，如果在一个控制周期内以非零矢量作为主矢量，零电压矢量作为辅助电压矢量，则可以实现主矢量修正误差、辅助矢量缓和脉动的控制效果，从而有效地改善PMSM 调速系统的稳态性能。图4 为PMSM 调速系统转矩脉动最优DTC 控制框图。

图4 PMSM调速系统转矩脉动最优DTC控制框图Fig.4 Control diagram of torque ripple minimization DTC of PMSM speed control system

4.1 实现机理

本文所提出的转矩脉动最优DTC方法旨在追求整个控制周期内的转矩脉动最小。如图5所示为2种DTC方法转矩变化趋势图，图5中传统DTC在一个控制周期内以变化率s1持续增长，优化DTC在控制周期的后半段以变化率s2进行转矩增幅缓和，此举可以优化PMSM 调速系统的稳态性能，下文将对上述方法的实现机理进行详细阐述。

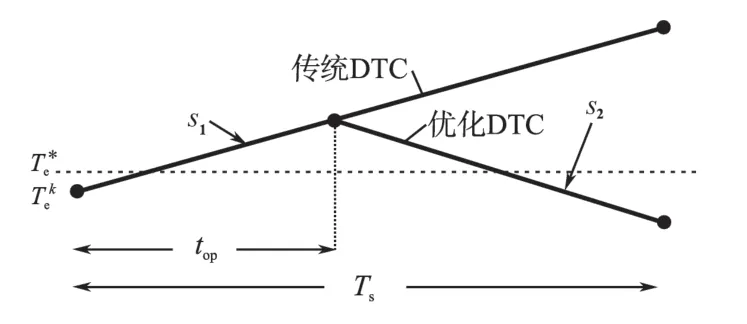
图5 2种方法转矩变化趋势图Fig.5 Diagram of torque change trend of two methods

为了实现一个控制周期内的转矩脉动均方根值最小，即

式中：kTs为第k控制周期的起始时刻；（k+1）Ts为第k控制周期的结束时刻。

采取占空比优化的方式进行DTC 转矩脉动优化，可将其在k控制周期内的转矩脉动值描述如下

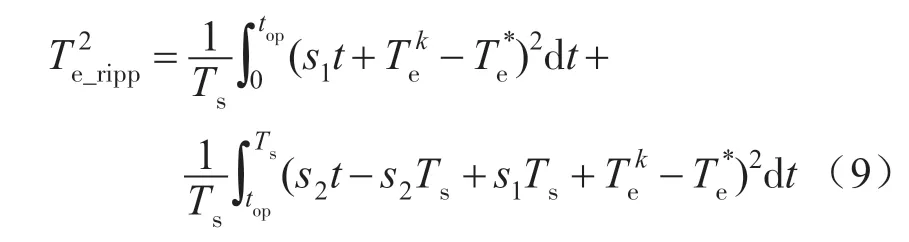
为了获得最优的转矩脉动控制效果需要合理地进行非零电压矢量作用时间top分配，式（9）给出了占空比优化时对应转矩脉动的一般性数学描述，分析可知式（9）为一个凸函数，其存在唯一的极值点。为此对下式进行微分可知

求解式（10）可得转矩脉动最优控制对应的非零电压矢量占空比top为

4.2 实现步骤

前文给出了2 种转矩脉动最优DTC 方法的实现原理，综上所述可将其实现步骤概括如下：1）确定主矢量。根据转矩和磁链滞环控制器的输出状态，结合定子磁链所处扇区号，查询表1所示的查找表即可确定主电压矢量；2）确定零矢量。以开关状态切换最小为原则，结合主矢量状态确定对应的零矢量，其中：u1（100），u3（010），u5（001）对应零电压矢量为u0（000）；u2（110），u4（011），u6（101）对应零电压矢量为u7（111）。3）占空比计算。根据主矢量变化率s1、零矢量变化率s2以及转矩跟踪误差，求解式（11）所示的最优电压矢量占空比函数，确定主矢量最优作用时间top；4）可行性判断。进行top取值的有效性判断。若top＜0或top＞Ts，说明即便在整个控制周期施加单一电压矢量仍无法满足动态跟踪需求，此时相应的修正top=0或top=Ts。

5 实验与分析

为了验证基于占空比优化的转矩脉动优化方法的可行性和优越性，搭建了一台如图6 所示的12 kW 的PMSM 调速系统实验样机进行验证分析。控制系统核心处理器为TI公司的32位浮DSP TMS320F28335，可以方便地实现本文的控制算法。实验中所需观测变量以100 kHz的采样频率导入PC 中，并采用Matlab 软件进行观测分析。实验样机的主要参数为：额定功率12 kW，额定电压128 V，定子电阻1.6 Ω，dq 轴电抗15 mH，转子磁链0.2 Wb，极对数3，DC 母线电压200 V，控制频率10 kHz。

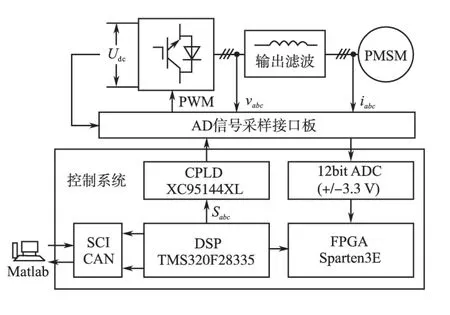
图6 PMSM样机系统硬件平台Fig.6 Hardware of the PMSM speed control system

图7 2种DTC方法稳态性能对比分析Fig.7 Steady state performance comparative analysis between two DTC methods

图7为2种DTC方法稳态性能对比分析结果，其中PMSM 运行于额定转速1 000 r/min、额定负载20 N·m 的工况下。可以看出，传统DTC 存在较大的转矩脉动现象，其转矩脉动范围高达25%，对应的定子电流也存在较大的纹波抖动。根据定子电流频谱分析结果可知，其总畸变率为9.87%，且谐波分量多集中于低频段；占空比优化DTC改善了转矩脉动现象，其转矩脉动范围被缩减至10%以内，对应的定子电流纹波抖动也较小。根据定子电流频谱分析结果可知，其总畸变率为5.45%，且存在集中于可知频率附近的高次谐波。

图8 为2 种DTC 方法动态性能对比分析结果，其中PMSM 运行于额定转速1 000 r/min、负载转矩在t=0.04 s 时由空载（0 N·m）突变至额定负载（20 N·m）。由图8 可知，当负载突变时，系统仅需5 ms左右的时间即可完成转矩响应，同时定子电流动态过程中不存在过大的超调现象，2种DTC 方法均保持着极为优异的转矩响应性能。至此可知，占空比优化DTC 保留传统DTC高动态响应的优异特性。

图8 2种DTC方法动态性能对比分析Fig.8 Dynamic state performance comparative analysis between two DTC methods

为了更进一步验证占空比优化DTC 在全速度范围内的优异品质，图9 给出了全速范围内两种DTC 方法的统计结果，其中包括：定子电流畸变率和开关频率两部分。可以看出，在全速度范围内优化DTC均保持着更低的定子电流畸变率，其稳态性能比传统DTC 更为优异。此外，传统DTC开关频率随着工作点的变化而发生变化，其变化范围在4～8 kHz之间，而优化DTC开关频率则维持在5 kHz 附近波动，该特性在功率开关器件及滤波装置的选型时优势明显。

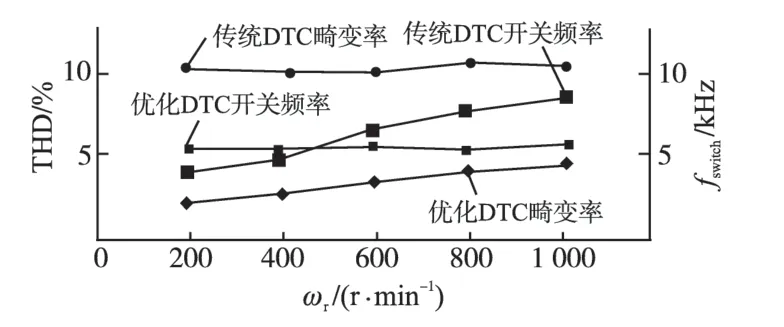
图9 全速范围内两种DTC方法统计结果Fig.9 Statistical results of two DTC methods in full speed range

6 结论

本文针对PMSM 调速系统传统DTC 方法存在的转矩脉动问题，提出了一种基于占空比优化的DTC控制方法，实验样机结果验证了该方法的可行性和有效性，具体可以得出如下几点结论：

1）占空比优化DTC 通过在一个控制周期内输出1 个非零电压矢量和1 个零电压矢量，可以有效地缓解单一电压矢量调节出现的转矩调节力度过强或过弱问题，从而改善了PMSM调速系统的稳态控制精度；

2）占空比优化DTC保留了传统DTC高动态响应的优异特性，在负载转矩发生大范围变化时，其仅需不足5 ms的时间即可完成转矩跟踪；

3）占空比优化DTC可以克服传统DTC开关频率随工作点变化的问题，为功率器件选型和滤波装置设计带来便利。

［1］Casadei D，Profumo F，Serra G.FOC and DTC：Two Viable Schemes for Induction Motors Torque Control［J］.IEEE Trans.on Power Electron，2002，17（5）：779-787.

［2］Takahashi I，Noguchi T.A New Quick-response and High-efficiency Control Strategy of an Induction Motor［J］.IEEE Trans.on Induction Application，1986，22（5）：820-827.

［3］李耀华，郭巧娟，吴俊，等.永磁同步电机直接转矩控制系统开关表分析［J］.电气传动，2012，42（11）：15-17.

［4］李耀华，刘晶郁，张德鹏，等.电动汽车用PMSM 直接转矩控制电压矢量选择策略［J］.电气传动，2012，42（6）：3-8.

［5］李君，李毓洲.无速度传感器永磁同步电机的SVM-DTC控制［J］.中国电机工程学报，2007，27（3）：28-34.

［6］Kenny B，Lorenz R.Stator and Rotor Flux Based Deadbeat Direct Torque Control of Induction Machines［J］.IEEE Transaction on Industry Application，2003，39（4）：1093-1101.

［7］Lascu C，Trzynadlowski A.Combining the Principles of Sliding Mode Direct Torque Control and Space-vector Modulation in a High Performance Sensorless AC Drive［J］.IEEE Transaction on Industry Application，2004，40（1）：170-177.

［8］Romeral L，Arias A.Novel Direct Torque（DTC）Scheme with Fuzzy Adaptive Torque -ripple Reduction［J］.IEEE Trans.on Industrial Electronics，2003，50（3）：487-492.

［9］Lascu C，Boldea I，Blaabjerg F.A Modified Direct Torque Control for Induction Motor Sensor-less Drive［J］.IEEE Transaction on Industry Application，2000，36（1）：122-130.