我国股票期现货市场间的溢出效应研究
——基于1分钟高频数据的实证检验
2015-06-24李保林阿布都瓦力艾百
李保林 阿布都瓦力·艾百
(中央财经大学金融学院,北京 100081)
我国股票期现货市场间的溢出效应研究
——基于1分钟高频数据的实证检验
李保林 阿布都瓦力·艾百
(中央财经大学金融学院,北京 100081)
本文以我国沪深300股指期现货为研究对象,采用2012年4月16日—2014年3月20日的1分钟高频交易数据,通过构建多元DCC-VARMA-GARCH模型检验了我国股指期现货市场之间的溢出效应。实证结果表明,我国股指期现货市场之间存在双向波动溢出效应,且现货市场的波动溢出效应大于期货市场,而均值溢出效应仅表现为期货市场向现货市场的单向传递。这说明我国股指期货市场已具备基本的价格发现功能,发挥了稳定股票现货市场的作用。
股指期货;溢出效应;DCC-VARMA-GARCH模型
一、引言
随着我国金融体系的不断完善,各金融市场间的联动性日益加强,市场波动不仅受到自身影响,同时还可能受其他市场制约。市场间的这种波动溢出效应可能存在于不同类型的金融市场之间,也可能存在于不同地域的市场之间。罗斯(Ross,1999)认为股票市场的波动与信息流密切相关,波动溢出的方向代表了信息的传递方向。因此,研究者可以通过对市场间波动溢出效应的分析来了解波动风险的传递方向和路径,同时还可以掌握信息在市场间的传递模式。
股指期货是以股价指数作为标的物的金融衍生产品,其交割价格采用到期日的股票指数,因此一个市场波动会对另一个市场产生影响,这种内在关联性导致两市场价格具有一定程度的内生性。股票市场作为宏观经济的“晴雨表”,股价指数在反映宏观经济状况方面具有一定的先行性;股指期货则为投资者提供针对股票投资(组合)进行避险、投机和套利的渠道。实证研究也表明,由于股指期货的保证金制度及双边交易等优势,市场往往对新的信息冲击能够做出及时的调整,从而定价效率高于现货市场(谢,1999)。所以,股指期货自问世以来,在国际期货市场呈现高速增长,成为重要的金融期货品种。自2010年4月16日我国推出沪深300股指期货合约至今,金融期货市场已走过了4个年头,从最初的重新起步发展成为投资者控制系统风险的重要场所。本文对股指期现货市场溢出效应进行研究,有助于我们了解我国股市的波动风险来源和传导路径,进一步揭示两市场间的信息传导和波动的相互关系,同时也为政府金融监管提供启示和决策依据。
二、文献回顾
国外关于股指期货与股票市场协同性的研究起步较早。在均值溢出效应方面,陈(Chan,1992)采用ARMA时间序列模型检验了标普500指数和MMI股指在正/负面消息冲击下的期现货价格的领先与滞后关系,并探讨了系统冲击下的期现货间的价格关系,得出期货价格领先现货价格的结论。金、斯卡莫里与施瓦兹(Kim、Szakmary与Schwarz,1999)对S&P500、NYSE Composite及MMI指数期货与现货进行分析,研究发现,任何市场的冲击均能迅速传递至其他市场,但反应时间则因市场来源不同而存在差异,其中S&P500指数的反应最为领先。沙特拉斯等(Chatrath等,2002)利用1993—1996年的日内15分钟高频数据,采用VAR模型分析了S&P500指数期现货市场的领先滞后关系,结果发现,不同的市场行情下期现货市场的溢出程度不同。博尔等(Bohl等,2011)采用DCC-GARCH模型研究了波兰股指期货市场的领先滞后关系和波动溢出效应,发现随着机构投资者参与期货市场的不断深入,波动开始由期货市场向现货市场传导。
在股指期货市场与股票市场的波动溢出效应方面,安东尼奥与霍姆斯 (Antonio与 Holmes,1995)研究了FT-SE100股指期货上市后对股价波动性的影响,实证结果表明,期货上市导致了股票现货波动增强。谢(Tse,1999)采用EGARCH模型分析了美国股指期现货市场的溢出效应,结果发现,以道琼斯工业平均指数(DJIA)为标的的期现货市场之间存在非对称双向波动溢出效应,即利空大于利好,期货大于现货。张等 (Chang等,1999)以日经225指数与对应的股指期货为样本,研究了日经225股指期货上市前后市场条件波动性的变化,实证结果发现期货交易会增加现货投资组合的条件波动性,通过股价指数成分股部分可以观察到期货与现货市场间存在波动的双向回馈现象,但对于没有期货交易的股票则不存在波动性外溢的情形。
我国股指期货市场起步较晚,国内在这方面的研究也较少,结论也存在较大差异。邢天才、张阁(2009)研究了新加坡新华富时A50股指期货对沪深300指数的影响,发现股指期货的推出轻微地增大了现货市场的波动性,同时信息对现货市场的冲击更强。封思贤等(2010)研究了境外异地上市的香港H股指数期货与新加坡新华富时A50指数期货对国内现货市场的价格发现和波动溢出的影响,发现香港H股股指期货对大陆股市具有溢出效应,而新华富时A50指数期货对大陆股市的溢出效益不显著,更多的是受大陆本土市场的影响。文凤华等(2011)采用修正的BEKK-GARCH模型,运用2010年4—6月间的5分钟高频数据检验了沪深300股指期现货之间的动态关系,认为两个市场间存在双向波动溢出效应。乔高秀、刘强(2012)采用2010年4月16日—2011年7月15日期间的1分钟高频数据,将样本分成3段进行检验,结果发现,整个样本期内股指期现货市场之间存在双向的波动溢出效应,并且市场间的波动溢出效应和误差修正项的影响在不同阶段的表现不同。
由于我国股指期货推出时间不长,针对沪深300股指期货上市交易后我国股指期货市场和股票现货市场溢出效应的相关研究样本时间较短,且结论尚不统一。本文从均值溢出和波动溢出两方面对两市场之间的溢出效应进行系统研究。均值溢出主要从收益率的一阶矩角度考察两市场之间的关系,能够解释两市场之间价格的领先与滞后关系;波动溢出从收益率的二阶矩角度考察两市场之间的关系,能够解释一个市场的波动对另一市场波动的影响。
在研究方法上,国内现有文献大多采用BEKKGARCH模型的形式来研究不同市场之间的波动溢出关系,然而BEKK模型在参数识别和经济解释问题上不够明确,在实际应用中也存在难以克服的障碍。而近年来在金融市场动态相关性研究中得到广泛应用的DCC-GARCH模型则更简洁,在估计大规模的相关系数矩阵时更具计算优势。然而DCC-GARCH模型只能用来刻画市场之间的动态相关系数,不能具体分析市场之间的波动溢出效应。因此,本文尝试通过构建DCC-VARMA-GARCH模型作为方差方程来弥补上述方法的不足,通过对股指期现货市场之间的时变相关性以及收益(线性)和波动(非线性)的关系进行系统的研究,以此更好地解释股指期货市场和股票现货市场之间的导向关系以及波动聚集效应和溢出效应,从而准确地把握两市场之间的动态变化关系以及他们之间的信息传导机制。
三、研究方法及模型的构建
在满足有效市场假定条件下,股指期现货价格能够对市场冲击同时做出相同的反应,两者在长期应处于相对均衡稳定的状态。但由于市场流动性、交易制度等因素的影响,二者对同一信息的反应速度并不相同,因此造成期现价格的短期偏离。因此,为体现股指期现货市场之间的长期均衡关系及短期的动态调整过程,本文将条件均值方程设定为向量误差修正的形式。
针对股指期现货收益率的方差协方差矩阵具有时变性和波动聚集性的特点,恩格尔(Engle,2002)提出了动态相关系数的DCC-GARCH模型,能够较好地刻画金融市场之间的协同性。然而DCC-GARCH模型的研究对象仅限于市场之间的动态相关系数,无法具体分析市场之间的波动溢出效应,而林和麦卡利尔(Ling和McAleer,2003)提出的VARMAGARCH模型以及麦卡利尔、霍蒂和利伯曼(McAleer、Hoti和Lieberman,2008)提出的VARMA-AGARCH模型,将方差方程扩展成VARMA的形式,以考察变量冲击的交叉及非对称影响。本文将标准的DCC-GARCH模型和VARMA-GARCH模型结合成DCC-VARMA-GARCH模型作为方差方程,来研究我国股指期货市场和股票市场的动态相关性和溢出效应。
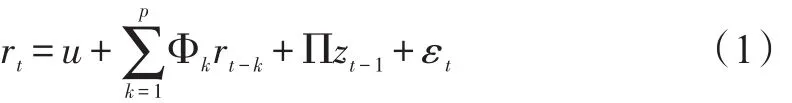
将均值方程与方差方程联合估计的VECM-DCCVARMA-GARCH模型的均值方程表示为①:场,2代表股票市场),为滞后项系数矩阵, zt-1=ft-1-δst-1表示误差修正项,反映变量之间的长期均衡关系的偏离,为误差修正项的系数向量,为残差项向量。
模型的方差方程部分采用DCC-VARMA-GARCH(1,1) 的 形 式 , 方 程(1)中 残 差 向 量εt|It-1∼N(0,Ht), It-1为 t-1 时 刻 的 信 息 集 ,
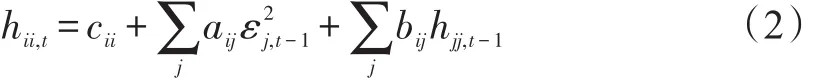
在恩格尔(2002)提出的DCC模型中,Qt的结构被设定为:
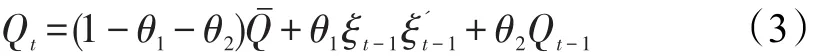
在均值方程(1)中,如果所有ϕk,21均为零或不显著,则说明不存在股指期货市场向现货市场的均值溢出;如果所有ϕk,12均为零或不显著,则说明不存在股票市场向股指期货市场的均值溢出。均值溢出效应的检验其实质就是单方程系数的联合显著性检验,对应的统计量为:
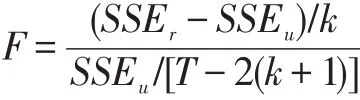
其中,SSEr为约束条件下的残差平方和,SSEu为无约束下的残差平方和,k为待检验系数的个数,T为总样本量。
条件方差方程(2)可具体写为:
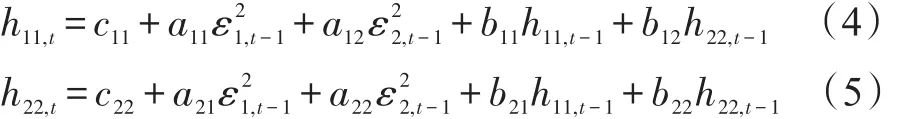
方差方程探讨了两市场收益率滞后1期的残差平方与条件方差的影响因素,参数a11、b11与a22、b22分别代表期现货市场波动的持续性,a11、b11或者a22、b22均为零或不显著,说明市场自身滞后1期残差项平方和滞后1期条件方差对当期条件方差无影响。a12、b12体现了股票市场对期货市场的ARCH型和GARCH型波动溢出效应,如果a12、b12同时为零或不显著,说明股票市场收益率残差项平方和方差的滞后1期对当期期货市场条件方差无影响。a21、b21则反映期货市场对股票市场的波动溢出效应。本文采用似然比法检验市场间的波动溢出效应,检验统计量为:
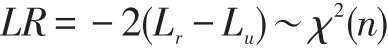
其中,Lr、Lu分别为模型有约束和无约束时的对数似然函数值,n为受约束参数的个数。
四、实证检验
(一)样本选取及数据描述
我国上市交易的沪深300股指期货合约分为当月、下月及随后的两个季月。由于股指期货合约的交易主要集中在当月合约,因此本文选取在中国金融期货交易所上市的沪深300股指期货当月连续合约序列(IFL0)作为期货合约的代表,选取沪深300股价指数代表股票市场,研究的样本为从2012年4月16日—2014年3月20日的日内1分钟数据。由于我国股指期货市场和股票市场在交易时间上有差异,指数期货市场的交易时间为上午9:15—11:30,下午13:00—15:15,而股票市场的交易时间为9:30—11:30,下午13:00—15:00,考虑到协整分析的需要,我们选取两市场交易时间重叠部分的数据。由于金融资产价格变化幅度大,通常为非平稳序列,本文采用具有良好统计特征的对数收益率形式,t期的收益率可表示为rt=100log(Pt/Pt-1)。所有数据均来源于万得资讯。
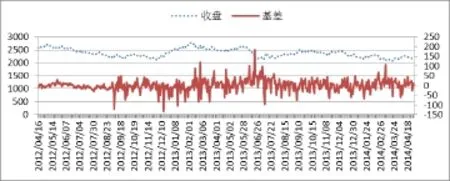
图1:沪深300股指收盘价及基差走势图
到期交割制度使得股指期货与股指现货之间存在一定的关联性。本文将股指现货收盘价与股指期货收盘价的差定义为基差②。首先考察沪深300股指收盘价与基差间的波动关系(见图1)。从图1可以看出,股指期货经过两年的发展,市场运行逐步稳定和健全,投机以及套利者的参与,使得基差在样本期间的大部分时间内围绕零上下波动,这种趋于收敛的性质初步显示我国期现货市场间的互动关系及市场间密切的信息传递。
表1给出了收益率序列的基本统计特征,从表中可看出,沪深300股指期货与现货的收益率均值都为负,期指收益率的标准差大于现货,表现出更大的波动性,这与股指期货市场的杠杆效应有关。从偏度和峰度上来看,股指期货指数表现为左偏而现货指数表现为右偏,而且两者的峰度都大于3,均表现出尖峰厚尾特征。而两收益率序列的JB统计量也都拒绝了服从正态分布的假设。对收益率序列进行多元混合检验③的多元Ljung-Box Q统计量显示,两市场收益率和收益率平方项均存在自相关和交叉相关,因此需要针对两收益率之间的一阶矩和二阶矩建立多元模型来研究两市场收益率和波动率之间的溢出效应。

表1:沪深300股指期货和现货收益率的基本统计特征
(二)平稳性检验
首先,对沪深300股指(S)和股指期货(F)的价格对数序列进行单位根检验。由检验结果可知,对于两序列存在单位根的原假设均未被拒绝。而对对数收益序列进行平稳性检验结果显示,在1%水平下拒绝原假设,即S和F为I(1)过程, rs和rf为I(0)过程。
然后对两收益率序列进行Johansen协整检验,结果如表2所示。从表中可看出,股指期现货价格之间存在协整关系,因此,在设定均值方程时我们可以加入误差修正项以考察其对两市场的影响。
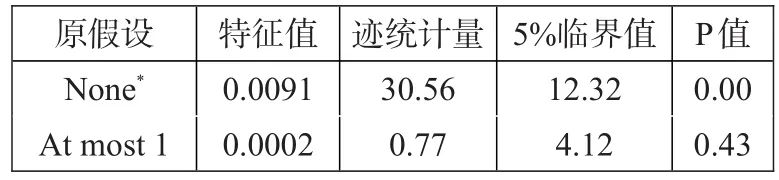
表2:沪深300股指期、现货对数价格的协整检验结果
(三)参数估计及检验
根据AIC信息准则,误差修正模型的最优滞后阶数取为15。我们首先对所设定的模型进行诊断检验,对二元标准化残差进行混合检验,应用二元Ljung-Box统计量,有Q2(5)=23.93(0.25),Q22(5)=
6.98(0.99),括号内的数表示 p值,从而说明所拟合模型的残差不存在显著的序列相关性或条件异方差,模型能充分描述条件均值和波动率的特征。参数估计结果如表3所示。
1.在均值方程的估计结果中,若参数ϕk,1j均不显著,则表明股指期货收益率不存在自相关,也不受股票市场前期收益率的交叉影响。而参数ϕk,2j均显著,说明指数收益率存在自相关和期货前期收益率的影响,股指期货具有领先作用。结果表明,在5%的显著性水平下,误差修正项系数 β1和 β2均显著,但 β2绝对值大于 β1绝对值,说明误差修正项对期货市场影响更大,即当指数期现货价格偏离长期均衡时,投机和套利将驱使价格向均衡调整,期货市场的高杠杆导致期货价格波动更大。
2.在方差方程中,若系数矩阵A和B中的所有对角元素均大于零,且在1%的显著性水平下显著不为零,说明股指现货和股指期货收益率均存在ARCH效应,aii 非对角元素只有a21不显著,而其他3个元素均在1%的显著水平下拒绝原假设,表明两市场间存在波动溢出效应。在短期的溢出效应上,a12显著为负而a21不显著,说明股票市场前期未预期到的冲击会减小当期股指期货市场的波动性,而股指期货市场前期未预期到的冲击对当期股指期货市场的波动性没有显著的影响。从长期来看,b21<0 3.在动态相关系数方程的估计中, θ1+θ2<1,表示两市场的相关系数的变化具有持久性,而θ1<θ2则表明相关系数受前期未预期到的信息冲击影响较小,而主要受前期相关系数的影响。 4.为了更严格地说明股指期货市场与股票市场之间的均值溢出和波动溢出效应,分别对均值方程和方差方程进行F检验和似然比检验,结果如表4所示。均值溢出效应的检验结果显示:在1%的显著性水平下,原假设ϕ1,12=ϕ2,12=ϕ1,21=ϕ2,21=0被拒绝,表明我国股指期现货市场之间存在均值溢出效应。对溢出方向进行检验时,在5%的显著性水平下原假设ϕ1,21=ϕ2,21=0被拒绝,而 ϕ1,12=ϕ2,12=0被接受,说明在均值溢出效果上只存在期货向现货市场的单向溢出,我国股指期货市场的信息传递速度快于现货市场,具有较强的价格发现功能。这一方面是由于股指现货没有交易,并且对信息冲击的调整速度较慢;另一方面在于期货市场的高流动性、低交易成本及卖空机制等优势,吸引了大量投机者,价格对信息反应更快。 表3:VECM-DCC-VARMA-GARCH模型的参数估计结果 表4:股指期货市场与股票市场溢出效应检验 在表4的两市场波动溢出效应的检验中,从LR统计量的显著性上可以看出,在1%的显著性水平下,我国股指期现货市场之间存在双向的波动溢出效应。另外,67.34>10.10,与前面的参数估计结果|a12|>|a21|和|b12|>|b21|一致,反映了我国股指期货市场与股票市场的波动溢出效应具有一定的非对称性,即我国股票现货市场的波动溢出效应比股指期货市场要更显著,这与股票市场(T+1)和期货市场(T+0)的交易制度有关,而且期货市场允许双边交易。因此,面对来自股票市场的波动,股指期货市场的交易制度允许投资者在更短时间内进行买卖操作,从而迅速地改变投资方向和持仓量,进而使股指期货市场表现出更大的波动性。 本文以沪深300股指期现货为研究对象,利用近两年市场交易1分钟高频数据,构建了VECM-DCCVARMA-GARCH模型,对我国股指期货市场和现货市场的动态相关关系及溢出效应进行了实证检验,主要结论如下: 一是我国的股指期现货市场之间存在长期均衡关系,但二者之间只存在期货向现货市场的单向均值效应,期货市场对信息的反应快于指数。 二是我国股指期货和股票市场均受到自身前期未预期到的冲击和前期累积信息的影响,期货市场将前期未预期到的冲击转化为条件方差的速度更快,而信息对股票市场波动影响的持续性更强。 三是我国股指期现货市场之间存在双向的波动溢出效应,且期货市场的波动溢出效应小于股指现货市场。从短期来看,股票市场前期未预期到的冲击会减小当期股指期货市场的波动。从长期来看,指数前期的波动加剧了期货市场当期的波动,而期货市场前期的波动则减缓了当期指数的波动。 研究表明,经过4年的发展,我国股指期货已具备较好的价格发现功能,股指期货的推出并没有导致现货市场波动的增加,反而在本质上起到了稳定股票市场的作用,其高效获取市场信息的能力和价格发现功能已初步显现。随着交易和监管制度的不断完善,我国股指期货市场与现货股票市场的互动关系及市场间信息传递过程将更加密切,银行等大型机构投资者的参与将进一步提高期货市场的运行效率。对于监管当局来说,应转变监管方式,未来以功能型监管为主,放宽市场准入门槛,加强投资者教育,提高市场的透明度,让期货市场成为一个真正为机构投资者服务的避险和保值市场。 注: ①一般情况下,可以对VECM模型和GARCH模型分两步估计,也可以直接对VECM-GARCH模型进行联合估计,样本容量足够大时这两种方式是渐近等价的(谢,1999)。 ②由于期现货交易的非同步,这里我们让基差=股指现货收盘价-股指期货收盘价,虽有偏差但不影响结论。 ③多元混合检验的详细介绍及模型诊断方法请参见王明进(2010)的相关文献。 [1]Chan,K.1992.A further analysis of the leadlag relationship between the cash market and stock index futures market[J].Review of Financial Studies,5. [2]Minho Kim,Andrew C.Szakmary,Thomas V. Schwarz.1999.Trading Costs and Price Discovery Across Stock Index Futures and Cash Markets[J].Journal of Futures Markets. [3]Chatrath A.,C.David,K.Dhanda,et al.2002.Index Futures Leadership,Basis Behavior and Trader Selectivity[J].The Journal of Futures Market,22. [4]Antonios,A.,P.Holmes.1995.Futures Trading and Spot Price Volatility:Evidence for FTSE-100 Stock Index Futures Contract Using GARCH[J].Journal of Banking&Finance,19. [5]Chang,E.C.,J.W.Cheng,J.M.Pinegar.1999. Does futures trading increase stock market volatility? The case of the Nikkei stock index futures markets[J]. Journal of Banking and Finance,23. [6]Robert Engle.2002.Dynamic conditional correlation-a simple class of multivariate garch models[J].Journal of Business and Ecomomic Statistics,20. [7]Bohl M.T.,C.A.Salm and M.Schuppli.2011.Price Discovery and Investor Structure in Stock Index Futures,Journal of Futures Markets,31(3). [8]Tse Y..1999.Price Discovery and Volatility Spillovers in the DJIA Index and Futures Markets,Journal of Futures Markets,19(8). [9]陈国进,许德学,陈娟.我国股票市场与外汇市场波动溢出效应分析[J],数量经济技术经济研究,2009,(12). [10]陈蓉,郑振龙.期货价格能否预测现货价格[J].国际金融研究,2007,(9). [11]陈昭.沪深300股指期货价格发现功能研究[C].华东交通大学学位论文,2012. [12]封思贤等.从中国股指期货境外的联动看我国股市定价权[J].金融研究,2010,(4). [13]胡秋灵,马丽.我国股票市场和债券市场波动溢出效应分析[J].金融研究,2011,(10). [14]高金余,刘庆富.伦敦与上海期铜市场之间的信息传递关系研究[J].金融研究,2007,(2). [15]李成,马文涛,王彬.我国金融市场间溢出效应研究——基于四元VAR-GARCH(1,1)-BEKK模型的分析[J].数量经济技术经济研究,2010,(6). [16]李文君,尹康.多元GARCH模型研究述评[J].数量经济技术经济研究,2009,(10). [17]寇明婷等.农产品期货市场与股票市场的互动关系研究——基于多元VAR-GARCH的检验[J].经济经纬,2011,(3). [18]刘成立,王朝晖,郑蓉.沪深300股指期货价格发现功能实证研究[J].价格月刊,2010,(10). [19]刘维奇,谢黎旭.权证市场和基础市场关系研究[J].数量经济技术经济研究,2008,(1). [20]刘凤根,王晓芳.股指期货与股票市场波动性关系的实证研究[J].财贸研究,2008,(3). [21]乔高秀,刘强.沪深300股指期货与现货市场价格波动与波动溢出效应——基于十五个月高频数据的实证研究[J].投资研究,2012,(8). [22]邢天才,张阁.股指期货的推出对现货市场影响的实证研究[J].财经问题研究,2009,(7). [23]史美景,邱长溶.股指期货对现货市场的信息传递效应分析[J].当代经济科学,2007,(4). [24]王朝晖,李心丹.股指期货市场与股票市场:信息传导与风险传递[J].社会科学战线,2013,(5). [25]魏振祥等.沪深300股指期货与国外股指期货市场间的信息传递效应[J].财贸经济,2012,(8). [26]左浩苗.基于高频数据的股指期货与现货市场波动溢出和信息传导研究[J].金融研究,2012,(4). The Spillover Effect Between the Chinese Stock Index Futures Market and the Stock Market——The Empirical Test Based on High Rrequency Data for 1 Minute Li Baolin Abduwali•Aibai Based on China's Shanghai and Shenzhen 300 stock index spot as the research object,adopted April 16,2012 to March 20,2014 1 minute high-frequency trading data,by constructing multivariate DCC-GARCH error correction model tested spillover effects of stock index futures and spot markets.The empirical results show that in our country there is a two-way volatility spillover effects between the stock index futures market and the spot market,and the mean spillover effect of one-way transmission from the futures market to the spot market.Besides,the spot market volatility spillover effect is stronger than the futures market,which shows that the stock index futures market in China already has the basic price discovery function,the introduction of stock index futures didn’t cause the increase of stock markets volatility,but played a role in stabilizing the stock spot market. stock index futures,spillover effect,DCC-VARMA-GARCH Model F830.91 :A :1674-2265(2015)05-0003-07 (特约编辑 张立光;校对 YJ,GX) 2015-4-15 国家自然科学基金项目:基于高频数据的金融市场间信息溢出与风险传染的微观机理、动态模型及其应用(项目号:71471182)。 李保林,男,安徽宿州人,中央财经大学金融学院博士,研究方向为国际金融与金融工程;阿布都瓦力·艾百,男,新疆乌鲁木齐人,中央财经大学博士,新疆财经大学讲师,研究方向为区域金融与金融市场。

五、结论与建议
(School of Finance,Central University of Finance and Economics,Beijing 100081)
