不定方程x3-125=2pqy2的整数解研究
2015-06-23李润琪
李润琪
(德宏师范高等专科学校数学系,云南 芒市 678400)
不定方程x3-125=2pqy2的整数解研究
李润琪
(德宏师范高等专科学校数学系,云南 芒市 678400)
设p,q为奇素数,p≡13(mod 24),q≡19(mod 24).运用Legendre符号的性质、同余的性质等得出了不定方程x3-125=2pqy2无正整数解的一个充分条件.
不定方程;整数解;同余;Legendre符号;奇素数
方程:

是一类基本而重要的三次不定方程,但目前结果还不多见,当D不能被6k+1形素数整除时其结论主要见文献[1-2];当D能被6k+1形素数整除时其结论主要见文献[3-8].本文主要讨论D含2,同时含2个6k+1形素因子方程x3-125=Dy2的整数解的情况.
引理1[9-10]设p,q,r为奇素数,p≡13(mod 24),q≡19(mod 24),,则Diophan⁃ tine方程x3-1=2pqry2仅有平凡解(x,y)=(1,0).
定理1 设p,q为奇素数,p≡13(mod 24),q≡19(mod 24)为奇素数,Legendre符号值,则不定方程:

仅有平凡解(x,y)=(5,0).
证明 当x≡0(mod 5)时,令x=5x1,则方程(2)可化为:

故由引理1得:方程(4)仅有平凡解(x1,y1)=(1,0),所以此时方程(2)仅有平凡解(x,y)=(5,0),故当x≡0(mod 5)时方程(2)在题设条件下仅有平凡解(x,y)=(5,0).
当x≢0(mod 5)时,此时5|/(x-5),则方程(3)为gcd(x-5,x2+5x+25)=1或3,又x2+5x+25≡0(mod 2),则方程(2)可分解为以下8种可能的情形:
情形Ⅰ:x-5=2pqa2,x2+5x+25=b2,y=ab,gcd(a,b)=1;
情形Ⅱ:x-5=2pa2,x2+5x+25=qb2,y=ab,gcd(a,b)=1;
情形Ⅲ:x-5=2qa2,x2+5x+25=pb2,y=ab,gcd(a,b)=1;
情形Ⅳ:x-5=2a2,x2+5x+25=pqb2,y=ab,gcd(a,b)=1;
情形Ⅴ:x-5=6pqa2,x2+5x+25=3b2,y=3ab,gcd(a,b)=1;
情形Ⅵ:x-5=6pa2,x2+5x+25=3qb2,y=3ab,gcd(a,b)=1;
情形Ⅶ:x-5=6qa2,x2+5x+25=3pb2,y=3ab,gcd(a,b)=1;
情形Ⅷ:x-5=6a2,x2+5x+25=3pqb2,y=3ab,gcd(a,b)=1.
下面分别讨论这8种情形下方程(2)的解的情况.
情形Ⅰ 由x2+5x+25=b2解得:x=-21,-8,-5,0,3,16代入x-5=2pqa2,得:2pqa2=x-5=-26,-13-10,-5,-2,11,显然无解,故该情形方程(2)无整数解.

情形Ⅲ 因为x2+5x+25=x(x+5)+25,而x与x+5奇偶性不同,故x(x+5)为偶数,则x(x+5)+25为奇数,即x2+5x+25为奇数.又p≡13(mod 24)为奇素数,则由x2+5x+25=pb2得:b2为奇数,即b2≡1(mod 8),则pb2≡5(mod 8).
因为q≡19(mod 24),由a2≡0,1,4(mod 8)得:2qa2≡0,6(mod 8),则x=2qa2+5≡3,5(mod 8),故有x2+5x+25≡1,3(mod 8),则有1,3≡x2+5x+25=pb2≡5(mod 8),矛盾,故该情形方程(2)无整数解.
情形Ⅳ 因为x2+5x+25为奇数,又p≡13(mod 24),q≡19(mod 24)为奇素数,则由x2+5x+25=pqb2得:b2为奇数,即b2≡1(mod 8),则pqb2≡7(mod 8).
由a2≡0,1,4(mod 8)得:2a2≡0,2(mod 8),则x=2a2+5≡5,7(mod 8),故有x2+5x+25≡3,5(mod 8),则有3,5≡x2+5x+25=pqb2≡7(mod 8),矛盾,故该情形方程(2)无整数解.
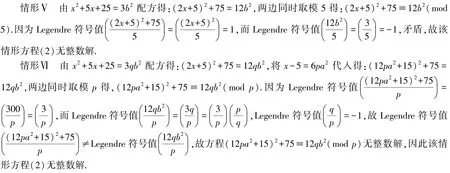
情形Ⅶ 因为x2+5x+25为奇数,又p≡13(mod 24)为奇素数,则由x2+5x+25=3pb2得:b2必为奇数,即b2≡1(mod 8),则3pb2≡7(mod 8).
因为q≡19(mod 24),由a2≡0,1,4(mod 8)得:6qa2≡0,2(mod 8),则x=6qa2+5≡5,7(mod 8),故有:x2+5x+25≡3,5(mod 8),则有:3,5≡x2+5x+25=3pb2≡7(mod 8),矛盾,故该情形方程(2)无整数解.
情形Ⅷ 因为x2+5x+25为奇数,又p≡13(mod 24),q≡19(mod 24)为奇素数,则由x2+5x+25=3pqb2得:b2为奇数,即b2≡1(mod 8),则3pqb2≡5(mod 8).
由a2≡0,1,4(mod 8)得:6a2≡0,6(mod 8),则x=6a2+5≡3,5(mod 8),故有x2+5x+25≡1,3(mod 8),则有:1,3≡x2+5x+25=3pqb2≡5(mod 8),矛盾,故该情形方程(2)无整数解.
综上有:当x≡0(mod 5)时方程(2)在题设条件下无整数解.
综上所述,不定方程(2)在题设条件下仅有平凡解(x,y)=(5,0).
[1]李复中.关于丢番图方程x3±125=Dy2[J].东北师范大学学报:自然科学版,1996(3):15-16.
[2]李复中.关于一类丢番图方程x3±(5k)3=Dy2[J].东北师范大学学报:自然科学版,1998(2):16-19.
[3]普粉丽,杜先存.关于不定方程x3±53=3Dy2[J].海南大学学报:自然科学版,2013,31(4):292-294.
[4]杜先存,刘玉凤,管训贵.关于丢番图方程x3±53=3py2[J].沈阳大学学报:自然科学版,2014,26(1):85-87.
[5]万飞,杜先存.关于丢番图方程x3±53=3py2的整数解[J].湛江师范学院学报,2014,35(3):5-6.
[6]普粉丽,杜先存.关于Diophantine方程x3-53=py2的解的研究[J].延安大学学报:自然科学版,2013,32(4):10-11.
[7]廖军,杜先存.关于Diophantine方程x3-53=2Dy2的整数解[J].长沙大学学报:自然科学版,2014,28(2):7-8.
[8]廖军.关于不定方程x3+53=Dy2的整数解[J].湖北民族学院学报:自然科学版,2013,31(3):275-277.
[9]管训贵.关于Diophantine方程x3±1=2pqry2的整数解[J].郑州大学学报:理学版,2015,47(2):49-52.
[10]钱立凯,杜先存.关于不定方程x3±27=py2[J].西南民族大学学报:自然科学版,2013,39(4):580-581.
[11]鲁伟阳,高丽,郝虹斐.关于不定方程x3-1=3Dy2整数解的讨论[J].云南民族大学学报:自然科学版,2013,22(4):264-265.
责任编辑:时 凌
On the Indefinite Equation x3-125=2pqy2
LI Runqi
(College of Mathematics,Dehong Normal College,Mangshi 678400,China)
Let p,q be odd primes,p≡13(mod 24),q≡19(mod 24).By using the nature of Legendre symbol and congruent,one sufficient condition is obtained that the indefinite equation in title has no inte⁃ger solutions.
indefinite equation;integer solution;congruent;Legendre symbol;odd prime
O156.1
A
1008-8423(2015)03-0268-02
10.13501/j.cnki.42-1569/n.2015.09.009
2015-06-28.
云南省教育厅科学研究项目(2014Y462).
李润琪(1965-),男,讲师,主要从事初等数论及数学教育的研究.
