基于相空间重构参数优化的风电功率混沌属性判定
2015-06-23潘捷陈丹霏王凌云
潘捷,陈丹霏,王凌云
(三峡大学 电气与新能源学院,湖北 宜昌 443002)
基于相空间重构参数优化的风电功率混沌属性判定
潘捷,陈丹霏,王凌云
(三峡大学 电气与新能源学院,湖北 宜昌 443002)
基于风电功率时间序列是一组非线性的随机序列,其内在规律复杂而多变,传统的预测手段很难对风电功率做出高精度的预测。研究风电功率内在特性是做出高精度预测的先行条件。相空间重构法能有效地展示非线性时间序列的内在混沌属性。采用C-C算法构造一个非线性时间序列的嵌入,有效减少计算的同时又保持了功率序列的非线性特性,并同步计算出嵌入维数和延迟时间。在重构的相空间基础上通过小数据量法计算出风电功率序列的最大李雅普诺夫指数,揭示了风电功率的内在特性,说明了风电功率混沌属性的判定原理和计算方法。
风功率预测;相空间重构;混沌属性;C-C算法;李雅普诺夫指数
1 引言
时间序列是指将某种现象某一个统计指标在不同时间上的各个数值,按时间先后顺序排1列而形成的序列,它是一组有序的随机数据,既包含数据的顺序,也包含数据的特性,可以通过对时间序列的分析,根据序列的过去值来预测未来值。时间序列不仅包含了所有变量过去的信息,而且还包含了参与系统演化的所有变量的大量信息。因此,对时间序列属性进行研究是选择合适的预测模型的基础。而风电场的发电功率都是按照一定周期采样和记录的,所以风电功率数据本身就是一个时间序列。但风电场发电功率往往具有随机性、不确定性和不可控性,传统的预测技术很难对风电功率做出高精度的预测[1-2]。充分了解和掌握风电场发电功率时间序列的属性则成为保证准确预测的前提。而理论上,更精确的预测方法应该用符合风电场发电功率特性的非线性动力学系统理论对其进行预测。
混沌时间序列分析是非线性时间序列分析的重要发展,其目前已经广泛的应用于生物医学、气象学、金融学等方向[3-4]。混沌现象是非线性动力系统中特有的一种运动形式,它是既普遍又极其复杂的形式。混沌现象的发现开创了科学模型的一个典范:一方面,混沌现象所固有的不确定性表明许多随机现象实际上是不可以预测的;另一方面,混沌现象对固有的对初值条件的敏感依赖性又意味着预测能力受到新的根本性的限制。所以混沌现象是短期可以预测,长期不可以预测的。因此,风电场发电功率内在混沌属性的分析,即风电功率的混沌识别,对于风电功率的短期预测具有重要的现实意义。如果风电功率时间序列具有混沌属性,则可借助于混沌动力学理论,应用混沌分析方法,建立基于混沌理论的风电场发电功率的预测模型,为风电场并网运行和调度提供依据。
本文基于我国某大型风电场的实际发电功率历史数据,对相空间重构的参数计算进行优化处理,采用C-C算法对风电功率时间序列进行相空间重构,同时计算出重构相空间的延迟时间和嵌入维度。在相空间重构的基础上采用小数据量法计算风电功率时间序列的最大Lyapunov指数,对Lyapunov指数曲线进行拟合,从而验证风电功率内部所包含的混沌属性。
2 风电功率时间序列的相空间重构
2.1 相空间概论
混沌系统内部的策动因素是相互影响的,在风功率时间序列上表现出先后产生的数据点是相关的,即任意时间点的功率值是由与之相互作用着的其他时间点的功率值所决定的。但传统的研究风电功率时间序列的方法,往往并不能够发现其中所蕴含的相关信息,出现这种情况的原因是非线性系统的相空间维数通常很高,在传统的低维空间因噪声干扰、测量手段的影响使非线性系统的轨迹出现混乱、复杂的特性,其内部所包含的信息不能被直接观测[5]。
混沌时间序列的识别与预测都是以相空间重构为基础。传统的低维坐标系无法揭示混沌系统的复杂动力学特征,而对于给定的时间序列,将其扩展到三维或者更高维的空间,以便将时间序列蕴藏的信息充分显露出来,这就是相空间状态重构法。
2.2 相空间重构技术
混沌时间序列重构相空间的方法主要有两种,一种是导数重构法,另一种则是坐标延迟重构法,而坐标延迟重构法在实际应用中比较普遍。相空间提出的最初目的是为了能在高维的相空间中把混沌吸引子恢复出来。混沌系统的特征之一就是混沌吸引子,指的是混沌系统运动轨迹最终会落入某一特定的轨道中,混沌吸引子就是这个轨道,体现了混沌系统具有规律性。
根据Takens的嵌入定理,对于任意时间序列,只要m≥2D+1(m是嵌入维数、D是动力系统的关联维数),在该m维重构空间里即可把吸引子恢复出来,重构空间中的相轨迹与原动力系统的微分同胚,重构空间与原动力系统拓扑等价。设时间序列为{x(i)},i=1,2,…,n,若嵌入维数为m,时间延迟为τ,则相空间重构为:
Ym(i)=[x(i),x(i+τ),…x(i+(m-1)τ)]i-1,2,…,N;N=n-(m-1)τ
(1)
其中,n为时间序列的长度;N表示重构后相空间的点数。
11月27日,云南省政府新闻办举行“壮阔东方潮 奋进新时代”云南省庆祝改革开放40周年系列新闻发布会经济发展主题新闻发布会,介绍了改革开放40年以来,特别是党的十八大以来,云南经济体制改革和经济发展方面的成就,一系列重大改革举措推动云南经济持续快速发展。
在相空间重构中,时间延迟τ和嵌入维数m为最重要的两个参数。目前,对于嵌入维数和时间延迟的选取方法中主要持有两种观点[6]。一种观念认为时间延迟τ和嵌入维数m是无关系的,可以各自进行独立选取。时间延迟τ的求法有自相关法、改进自相关法和互信息法等;嵌入维数m的求法有G-P算法、邻近点维数法、Cao方法等。通常情况下,时间延迟τ和嵌入维数m由上述的方法分别求取[7]。另外一种观点认为时间延迟τ和嵌入维数m是相互影响、相互关联的,可同时求取。经验证,τ与m并非各自独立的两个量,嵌入窗宽揭示了二者间的相关性:
τw=(m-1)τ
(2)
式中,τw为嵌入时间窗的宽度。
相比较其他方法,C-C方法在计算量的大小和操作的难易程度方面更占优势。C-C方法相对来说是比较简单的,在计算机上也很容易实现,虽然C-C方法没有比较坚实的理论基础,但是在实际应用中还是取得比较好的效果,并且很多的实验也表明C-C方法还具有抗噪的一面[8]。
3 C-C算法
依据公式(2)所给出的思路,本文采用能够同步计算嵌入维数m和时间延迟τ的C-C法对风电功率时间序列进行相空间重构[9]。对重构相空间的嵌入维数m和时间延迟τ进行联合计算。本文所采用某大型风电功率的采样数据如图1所示。
以m为嵌入维数,τ为时间延迟对时间序列x={x(i),i=1,2,…,n}进行相空间重构,先将混沌时间序列分解成长度为INT(N/t)的t个不相交的时间序列,INT为取整函数,t为一般的自然数。分解过程如下式:

图1 某大型风电场的风电功率采样数据
{x(1),x(t+1),x(2t+1),…}
{x(2),x(t+2),x(2t+2),…}
{x(t),x(t+t),x(2t+t),…}
(3)
其中每个子序列都为相空间中的一个m维相点,那么可以由以下公式来表示嵌入时间序列的关联积分:
(4)
式中:m为嵌入维;N为时间序列的长度;r为计算中所选取的搜索半径;τ为延迟时间;M=N-(m-1)τ,表示重构相空间后的相点个数;dij=||xi-xj||,表示一个无穷范数;θ是Heaviside函数,其表达式如下:
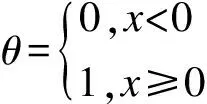
(5)
以上关联积分为一个累计分布函数,先设定一个用于比较两两相空间矢量距离的较小的定值r,然后将r与dij作比较,当dij>r取0,反之取1,最后得出距离小于定值r的量所占的比例,此值越小越好,越小越能说明重构的相空间有较好的一致性,也越接近与原始动力系统的结构。时间序x={x(i),i=1,2,3,…,n}的检验统计量如下定义:
S(m,N,r,τ)=C(m,N,r,τ)-Cm(1,N,r,τ)
(6)
上式的实际计算过程基于分解后的每个子序列,采用分块平均的方法,具体公式如下:
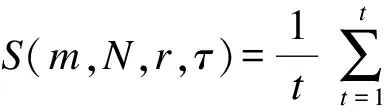
(7)
S(m,N,r,τ)反映了时间序列的自相关特性,最优时间延迟τ可取S(m,N,r,τ)的第1个零点,或者取S(m,N,r,τ)对所有半径r相互差别最小的时间点,此时表示重构吸引子的轨迹在重构相空间中完全展开,即相空间的点最接近均匀分布。
我们选取最大和最小的两个半径r,定义差量如下:
ΔS(m,N,r,τ)=max[S(m,N,r,τ)]-min[S(m,N,r,τ)]
(8)
S(m,N,r,τ)度量了S(m,N,r,τ)对所用半径r的最大偏差。由统计学的原理可知,r的取值在σ/2和2σ之间,m的取值在2和5之间。σ是时间序列的均方差。根据风电场的历史数据,这里我们取N=3000、m=2,3,4,5、ri=iσ/2(i=1,2,3,4)。计算:
(9)
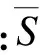
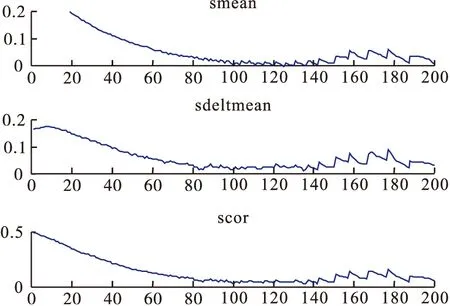
图2 C-C算法结果
4 风电功率时间序列的混沌属性判定
4.1 混沌属性的概念
目前混沌的概念尚未形成明确的定义,因此混沌信号特性识别的方法只是判别该时间序列是否为混沌的必要条件,主要包括定性,定量和两者结合三种方式。定性方法主要通过分析混沌信号在时域中的空间结构,以及在频域中频率特性,而与周期、准周期或随机相区别,包括相图法,功率谱法等。定性方法的优点是简单直观,但是过于笼统。定量方法则主要通过计算吸引子的特征量或其他参数来判定混沌时间序列,这些参数包括描述相邻轨道发散率的Lyapunov指数,刻画吸引子维数的关联维数,以及反映信息产生频率的Kolmogorov熵。本文将通过计算Lyapunov指数作为判定时间序列混沌属性的判据。由混沌运动的特征可知,两个相邻的初值所产生的轨道,随着时间推移将按指数分离,指数λ即用于定量描述这一现象,轨道的距离在相空间中分别表现为线度、面积与体积[10]。在时间序列的Lyapunov指数λ<0的方向,轨道运动稳定且相体积收缩,呈现出对初始条件不敏感;指数λ=0对应于稳定边界,属临界情况;指数λ>0的方向轨道快速分离,体现出对初始条件敏感,轨道运动呈现出混沌状态。所以,时间序列是否为混沌的一个判别依据就是该序列的Lyapunov指数是否大于零[11]。而在实际应用中,只需计算出时间序列的最大指数λ1,若其大于零则可判定该时间序列为混沌时间序列,进而可采用混沌理论进行分析和预测。
4.2 计算Lyapunov指数
通常计算最大Lyapunov指数的方法有Wolf法,Jacobian法,P-范数法,小数据量法等。为了减少人为因素影响和计算量,以及提高计算的效率和精度,本文将采用小数据量法。在前面C-C算法的结果基础上对风电功率时间序列x={x(i),i=1,2,3,…,n}进行相空间重构:
Ym(i)=[x(i),x(i+τ),x(i+2τ),…,x(i+(m-1)τ)] i=1,2,3,…,N;N=n-(m-1)τ
(10)
其中,m和τ分别为C-C法计算出的嵌入维数和延迟时间。
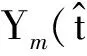
(11)
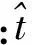
对相空间中的每个点Ym(t),计算出该邻域点对的i个离散时间步长后的距离:
(12)
最后相应于每一个i,对所有t的lndt(i)求平均值x(i):
(13)
式中:q表示非零dt(i)的数目,Δt为样本周期。并用最小二乘法做出回归直线如图3所示。
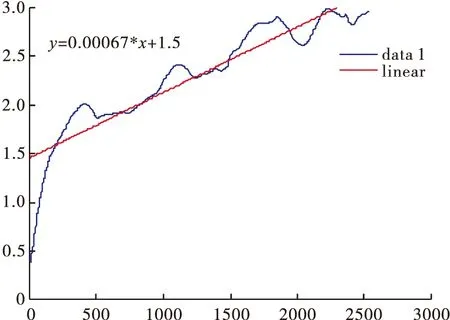
图3 小数据量法计算李雅普诺夫指数的结果
图中回归直线的斜率即为最大的Lyapunov指数λ1=0.00067>0,据此论证得出风电功率时间序列内部具有混沌属性。
5 结语
本文在matlab编程的基础上运用C-C算法对风电功率时间序列进行相空间重构,计算出嵌入维数和延迟时间。相较于传统的相空间重构法,对其参数的计算进行了优化,将时间序列蕴藏的信息一次性显露出来。在此基础上,用小数据量法计算出时间序列的最大Lyapunov指数,并证实其大于零,从而严格证明了风电功率时间序列具有混沌属性。为风电功率的混沌研究理论提供了必要条件和先行理论基础。
[1] 丁明,吴义纯,张立军.风电场风速概率分布参数计算方法的研究[J].中国电机工程学报,2005,25(10):107-110.
[2] 迟永宁,王伟胜,戴慧珠.改善基于双馈感应发电机的并网风电场暂态电压稳定性研究[J].中国电机工程学报,2007,27(25):25-31.
[3] 陈琢,钱鸣奇,童勤业.混沌态电阻测量电路的研究[J].电子测量与仪器学报,2003,17(3):46-51.
[4] 罗志增,李亚飞,孟明,等.脑电信号的混沌分析和小波包变换特征提取算法[J].仪器仪表学报,2011,32(1):33-39.
[5] 陶佳,张弘,朱国荣,等.基于优化相空间重构技术的风电场发电功率预测研究[J].电机工程学报,2008,32(4):56-60.
[6] 韩敏.混沌时间序列预测理论与方法[M].北京:中国水利水电出版社,2007:24-155.
[7] 冬雷,王丽婕,高爽,等.基于混沌时间序列的大型风电场发电功率预测建模与研究[J].电工技术学报,2008,23(12):125-129.
[8] 吕金虎,陆君安,陈士华.混沌时间序列分析及其应用[M].武汉:武汉大学出版社,2002.
[9] 陆振波,蔡志明,姜可宇,等.基于改进的C-C方法的相空间重构参数选择[J].系统仿真学报,2007,19(11):2527-2529.
[10] 邓重一.混沌预测方法及其应用研究[J].电源世界,2007(11):21-25.
[11] 屠强,衣立东,尚勇,等.电网区域化综合测风系统在风电开发中的应用研究[J].电网与水利发电进展,2008,24(1):3-7.
[12] 张国强,张伯明.基于组合预测的风电场风速及风电功率预测[J].电力系统自动化,2009,33(18):92-95.
Chaotic Property Determination of Wind Power on Parameter Optimization of the Phase Space Reconstruction
PANJie,CHENDan-fei,WANGLing-yun
(College of Electrical Engineering and New Energy,China Three Gorges University,Yichang 443002,China)
Wind power time series is a set of nonlinear random sequence,its inherent law is complex and changeable.It is difficult to make high precision prediction for wind power by the traditional prediction methods.It is the antecedent condition for the high precision prediction to research the wind power intrinsic characteristics.The chaotic properties of nonlinear time series can be effectively showed by the reconstruction method.In this paper,C-C algorithm is used to construct an embedding of the nonlinear time series,reducing the computation and keeping the nonlinear characteristic of the power sequence.The embedding dimension and the delay time are calculated synchronously.On the basis of the reconstruction,the small data quantity method is used to calculate the Lyapunov index,revealing the inherent characteristics of wind power and illustrating the judging principle of the wind power chaotic properties.
wind power prediction;phase space reconstruction;chaotic property;C-C algorithm;Lyapunov index
1004-289X(2015)02-0014-05
梯级水电站运行与控制湖北省重点实验室(三峡大学)开放基金课题(2013KJX09); 2014年三峡大学硕士学位论文培优基金项(2014PY033)
TM76
B
2014-12-18
潘捷,男,硕士研究生,研究方向为新能源发电技术。
