电缆载流量计算方法研究

刘哲,王炜,霍静文,冯超,吴震

(1.河北省电力勘测设计研究院，河北 石家庄 050031;2.石家庄供电公司,河北 石家庄050051;3.华北电力大学，北京 102206)

电缆载流量计算方法研究

刘哲1,王炜1,霍静文1,冯超2,吴震3

(1.河北省电力勘测设计研究院，河北 石家庄 050031;2.石家庄供电公司,河北 石家庄050051;3.华北电力大学，北京 102206)

对NM法、IEC法、数值计算法等多种电缆载流量计算方法进行了介绍，并进行了综合比较，提出了未来算法发展建议。

电缆;载流量计算;NM法;IEC法;数值计算法

1 引言

城市的电力输送越来越多地采用电缆的型式。电力电缆运行中，导体的温度是确定其载流量的依据，载流量是地下电缆运行中的重要参数，载流量偏大，造成缆芯工作温度超过容许值，电缆的绝缘寿命就比期望值缩短；若载流量偏小，则缆芯铜材或铝材就不能得到充分的利用，导致不必要的浪费[1]。

另一方面，在环境或负荷量改变的情况下，科学、合理地计算电缆载流量，实时预测电缆运行状态的热裕度、满载和过载能力，动态确定电力电缆线路载流量，有利于指导电力电缆设计、电力调度和电力电缆运行管理部门，在确保电力电缆有效安全寿命的前提下，有效、及时且充分地发挥现有电力电缆线路输电潜能。

目前，随着电力电缆线路越来越趋向于密集敷设、边界条件越来越复杂，研究载流量的计算方法是很有必要的。

2 NM电缆载流量计算方法

关于电缆载流量计算的研究最早开始于19世纪后期和20世纪初期，计算方法非常粗略和简单。随后Neher和McGrath进行了进一步的研究，并在1957年提出了关于电缆载流量及其温升的计算方法，后来被称为NM方法。他们首次较完整地研究了不同类型电缆的几何参数和安装条件对导体温度的影响，分析了电缆导体到周围环境中的温度分布和电缆的散热情况，并通过简化的热路模型计算出不同敷设条件下的载流量。

3 IEC标准电缆载流量计算方法

国际电工委员会(IEC)标准在1957年McGrath论文的基础上，结合1957年之后载流量的算法改进，于1982年提出了电缆额定载流量(100%负荷因数)计算标准IEC 60287,1985 年提出电缆暂态载流量计算标准IEC 60853。标准中给出的载流量计算方法与NM方法在原理上相似，它不仅包括了NM方法的全部计算公式，而且对不同电缆类型及敷设条件的载流量计算加以区分，将单芯电缆中的环流和涡流损耗计算扩展到有钢带的两芯和三芯电缆，并且添加了大截面分割导体电缆的涡流损耗计算(这点在NM方法中被忽略)，可以说它比NM的内容更全面。从形式上看，两者的计算公式似乎完全不同，这是因为两者所用的长度单位不同，NM方法的单位是英制单位(in)；而IEC标准中的单位是公制单位(m)，实质上是一致的。IEC 60287以后逐年进行了修正补充，已趋于完善。

目前各国电缆产品及其载流量大都已向IEC靠拢。国际上发达国家以及国际贸易都以IEC 60287标准作为制定电缆产品额定载流量的依据。我国电缆载流量方面的研究始于20世纪60年代中期。随着我国电工产品向IEC靠拢，电线电缆产品国家标准已基本等同IEC相应的标准，电缆载流量计算标准亦等同于IEC的相应计算标准。但我国尚未有对应于IEC 60853的国内标准。各国对电缆运行条件参量的期望值存有很大差别，IEC标准提倡从不同的角度出发，各个国家规定相应的值。

IEC 60287和IEC 60853是建立在解析和经验的基础上，而实际敷设情况是千变万化的，这就造成了IEC 60287和IEC 60853在很多场合下存在如下局限性。

(1)IEC 60287仅给出了单回路电缆的邻近效应计算公式，实际常常多个回路以集群方式敷设在一起，而回路间的电磁感应对电缆导体邻近效应的影响、对金属套内涡流损耗及环流损耗的影响等都不能忽略。

(2)IEC 60287标准是在给定电缆导体和金属套温度的基础上确定两者的电阻率，然后计算损耗，而实际中不同位置电缆的导体和金属套温度往往不同，导致电阻率不同、损耗不同，反过来又造成电缆的导体和金属套温度的不同，即温度场计算实际上是一个电磁场和热场的耦合计算问题。

(3)IEC 60287标准中对电缆间热效应的相互影响建立NM理论假设的基础上，利用镜像法进行计算。实际中地表不是等温面，电缆表面也不是等温面；地下深层温度保持在一个恒定的温度；电缆周围往往有回填土，并非敷设于单一介质中。因此，电缆集群方式敷设时电缆间热效应的相互影响不能按半无限大平面场利用镜像法进行叠加计算。

(4)对于电缆附近有外部热源(如热力管道)或局部穿过不利于热扩散区域等敷设情况下，标准中没有给定相应的计算公式。

(5)当前电力部门需要进行动态调整负荷，而这需要实时了解线路周围的相关环境参数和导体温度，并据此确定载流量。标准中给定方法对此无能为力。

4 数值计算方法电缆载流量计算方法

近二十年，随着计算机技术的飞速发展，数值计算在温度场计算中的应用越来越广泛，作用也越来越突出。目前，电缆温度场的数值计算方法主要有有限差分法、边界元法和有限元法等。下面分别对几种数值计算方法进行简单介绍[2-4]。

(1)有限差分法

在物理场数值分析的计算方法中，有限差分法是应用最早的一种。直到今天，它仍以其简单、直观的特点而被广泛应用着。有限差分法以差分原理为基础，它实质上是将物理场连续场域的问题变化为离散系统的问题求解，也就是通过网格状离散化模型上各离散点的数值解来逼近连续场域的真实解。在有限差分法中，在区域内根据位置来改变网格的步长是很费时的，而且在接近曲线边界时，边界就不可能与节点相一致，由此引起的误差不能忽视。因此，有限差分法很难表示复杂的边界条件，不易处理复杂问题。

采用有限差分法来计算电缆的散热情况。其数学模型为将整个土壤区域分为土壤、深层土壤，沙土等多个土区域(trench filling)(如图1所示)，不同的区域导热系数不同。地面和大气层之间存在导热和对流传热。导热算式由傅里叶公式确定，对流传热算式由牛顿公式确定。方程对于整个区域的每个特殊点均单独列出其热平衡表达式，以供编程时使用。计算中将电缆的表面看作等温体，当给定载流量时，可以确定电缆的表面温度；当给定电缆表面允许温度时，可以确定电缆的载流量。该方法的缺点是其程序不考虑电缆内部的结构，即假定各种类型、各种截面大小的电缆具有相同的载流量。2003年王增强等人采用有限差分法和坐标组合法相结合的方法，对土壤区域、电缆区域分别进行计算，最终确定电缆允许的载流量。虽然此方法考虑了土壤的水分迁移，也实测了不同土壤在各种条件下的导热系数，但由于预埋管方式的载流量影响因素较复杂，且各层导热系数不易确定，所以计算存在误差，缆芯载流量值不是特别准确。

(2)边界元法

边界元法与有限差分法相反，其所选择的函数满足区域内的支配方程，而后用这些函数去逼近边界条件。边界元法的优点在于考虑计算区域的边界，由于积分是在边界上进行的，采用此法可将三维的问题简化为二维问题、二维的问题化为一维问题来处理，使其数值计算较为简单。此外，由于此法是直接建立在基本微分方程和边界条件基础上，不需要事先寻求任何泛函，适当变换后，还能解决随时间变化的物理场问题。

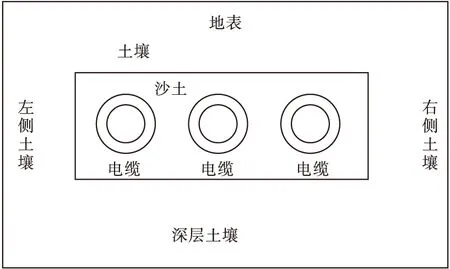
图1 单回路土壤直埋电缆温度场模型

1988年Gela采用边界元法来解地下电缆温度场，而不是计算区域的内部，这就使计算量从三维简化为二维。而且内部区域不需要划分网格，计算量明显低于区域型的计算方法，如有限元法或有限差分法。边界元法在无穷远处截断区域作为边界，不需像有限元法或有限差分法那样布置一个人为的边界，认为这个边界上的温度等于环境温度。但是当处理一个具有多层土壤的实际电缆沟问题或具有多根电缆铺设的问题时，边界元法的边界太多太复杂，计算量变得特别大。

(3)有限元法

有限元法在原理上是有限差分法和变分法中里兹法的结合。它对表示物理场的微分方程的变分问题作离散化处理，将场域划分为有限小的单元，并使复杂的边界分段属于不同的单元(如图2所示)，然后将整个场域上泛函的积分式展开成各单元上泛函积分式的总和。其中每个单元的顶点就是未知函数的取样点，它类似于差分法中的节点。各单元内试验函数采用统一的函数形式(如多项式等)，其待定系数取决于本单元各顶点上的函数取样值。泛函极小值的条件是泛函对试验函数中各待定系数的偏导数等于零，据此列出差分近似的代数方程组，并直接计算节点函数值的数值解，再确定试验函数以表示各单元内函数的近似解。

图2 典型电缆有限元剖分结构

1973年Flatabo通过有限元法计算地下电缆热暂态运行(热暂态指电缆运行中温度随时间变化的动态情况)的问题。采用泛函的变分计算，将变分问题转化为多元函数求极值的问题，取得近似解代替微分方程的求解。

1985年EL-Kady采用有限元法求解电缆管道外部(水泥槽和土壤之间) 的热阻。对所求的边界区域进行离散，建立离散方程，然后求解方程。该方法认识到了温度梯度造成的水分迁移以及水分含量对土壤导热系数的影响，但计算中仍忽略了水分迁移的影响，而且这些计算只应用于有限的条件。此后，Anders等人进一步利用有限元法对电缆的载流量进行了计算。近年来国内梁永春、孟凡风等人根据地表对流和深层土壤温度不变的原则，建立了电缆群温度场模型，将地下电缆群开域温度场等效为闭域温度场，利用有限元法分析了给定电缆负荷电流的地下电缆群闭域温度场分布，采用弦截法计算地下电缆群载流量，但仅考虑地下电缆群的温度场为稳态温度场，电缆群为等负荷、等截面。上述方法中，有限元法适合处理复杂的边界条件，对于分析复杂电缆群的温度场和计算载流量是一种有效的方法。

5 结论

现有国内外对电力电缆载流量基本计算方法都没有给出一种系统的、完整的方法，来解决载流量计算中存在的问题。由于环境和运行条件的差异，热阻系数、热源分布等诸多因素不易确定，载流量修正系数更是一个十分复杂的问题。

目前，大部分电缆生产厂家与设计院选择基于IEC标准的解析计算，其原因在于用简单的公式即可近似计算电缆的载流量；基于NM模型和IEC 60287标准的基础上，进行电缆载流量解析计算已沿用已久；对于具有简单结构和敷设的电缆系统而言，用数值计算反而更繁琐；考虑到实际电缆的结构和材料，单芯电缆的等效热路模型，由IEC 60287也可推广到多芯电缆。但解析法仅能解决一些几何上相对简单的问题。如在载流量计算中，公式中土壤的热传导率和热容设为常数，并假设大地表面为等温面，导体的电阻率为常数。数值计算的方法是在给定电缆敷设、排列条件和负荷条件下对整个温度场域进行分析，大地表面和电缆表面的温度都是待求量，更加接近实际边界条件。因此，数值方法更适合几何、物理上比较复杂的问题，在分析复杂电缆系统中有很大的灵活性，计算的结果也比解析算法更准确。

[1] 郑雁翎,王宁,李洪杰,等.电力电缆载流量计算的研究与发展[J].电线电缆,2010,02:4-9.

[2] 梁永春,柴进爱,李彦明,等.基于FEM的直埋电缆载流量与外部环境关系的计算[J].电工电能新技术,2007,4:10-13.

[3] 王有元,陈仁刚,陈伟根,等.基于有限元法的XLPE电缆载流量计算及其影响因素分析[J].重庆大学学报,2010,5:72-77.

[4] 付永长,张文斌,陈涛,等.不规则排列电缆温度场及载流量计算[J].电网技术,2010,4:173-176.

Investigation of the Calculaion Method of the Power Cable Current Rating

LIUZhe1,WANGWei1,HUOJing-wen1,FENGChao2,WUZhen3

(1.Hebei Electric Power Design & Research Institute,Shijiazhuang 050031,China;2.Shijiazhuang Power Company,Shijiazhuang 050051,China;3.North China Electric Power University,Beijing 102206,China)

The paper presents various calulating metholds of cable current-carrying capacity of N M,IEC and numberical methods and carries out synthetical comparision and future algorithm suggestions.

cuble;current carrying capacity;N M method;IEC method;numberical method

1004-289X(2015)02-0011-04

TM76

B

2014-12-18

刘哲(1982-)，硕士，河北承德人，毕业于华北电力大学，高级工程师，注册电气工程师，从事高压输电线路设计工作; 王炜(1971-)，本科，河北石家庄人，毕业于东北电力大学，高级工程师，注册电气工程师，从事高压输电线路评审设计工作; 霍静文(1989-)，本科，河北石家庄人，毕业于中国矿业大学，工程师，从事高压输电线路设计工作; 冯超(1975-)，本科，河北石家庄人，毕业于华中理工大学，高级工程师，高级技师，国家电网公司优秀专家人才; 吴震(1992-)，本科，安徽六安市人，毕业于华北电力大学，现在华北电力大学攻读电气工程专业硕士研究生。